下载文档原格式
课程名称《物理化学》2.1 自发变化过程的共同特征1、热力学自发过程热力学自发过程：不需要借助人为（非自然）外力就能够发生的过程；热力学非自发过程：必须借助人为（非自然）外力才能够发生的过程；（1）自发传热↓（2）自发混合（扩散）↓（3）自发化学反应298K 101kPa2H2(g) + O2(g) —————→ 2H2O(l)2、热力学可逆过程体系经过一过程，若体系与环境能同时复原，则称该过程为热力学可逆过程。
例：气体的可逆膨胀或可逆压缩例：1 mol理想气体，在273.2K下1：由202.6 kPa 等温恒外压膨胀到101.3 kPa ；W1 = －1136 J Q1 = 1136 J2：由202.6 kPa等温可逆膨胀到101.3 kPa ；W2 = －1574 J Q2 = 1574 J3：由101.3 kPa等温恒外压压缩到202.6 kPa ；W3 = 2272 J Q3 =－2272 J 4：由101.3 kPa等温可逆压缩到202.6 kPa；W4 = 1574 J Q4 =－1574 J求过程的△U、△H、W、Q。
解：理想气体等温过程：△U = △H = 0等温恒外压膨胀或压缩：W = －Q = －P外(V2—V1)等温可逆膨胀或压缩：W = －Q =－nRT ln(V 2/V 1)————————→结果：例：可逆传热过程例：在标准压强下，将1.80 kg 水从273 K ①用373 K 热源加热到373 K ；②可逆加热加热到373 K ，分析其可逆性。
已知：C pm = 75.8 JK -1 mol -1 解：加热过程：Q = n C pm (T 2－T 1)= 100×75.8×100 = 758 kJ体系降温复原：Q = n C pm (T 1－T 2)= －100×75.8×100 = －758 kJ可逆加热：准备从273 K 到373 K 的热源无穷多个，相临热源温度相差无穷小，让水依次在273 K 到373 K 热源上加热。
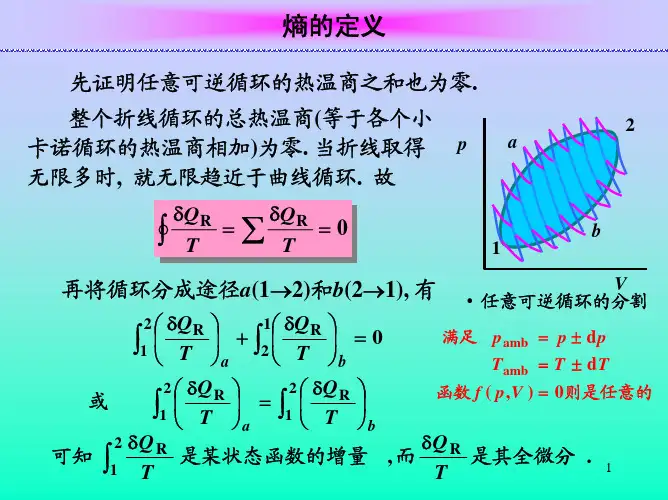
一、克劳修斯不等式：克劳修斯不等式说的是这个，先考虑一个热机H 和两个热源，假设两个热源1,2的温度分别是1T 和2T 并且有21T T ，然后热机H 从热源2吸热2Q ，从热源1吸热1Q （显然此处1Q 为负值），这时候这四个量满足： 02211≤+T Q T Q ……（1） 这个式子就是克劳修斯不等式最简单的形式，取等条件为当且仅当热机H 为可逆热机时。
当有不止两个热源的时候，（1）式可推广为：01≤∑=n i i i T Q ……（2） 熵变A →B 的定义式为：A B S S S-=∆ (3)对于可逆过程： S T Q∆=δ (4)对于不可逆过程：S T Q∆ δ (5)热力学第二定律的数学表达式为：T QS δ≥d 这里的温度T 只能理解为环境的温度。
对于不可逆过程的熵变，必须模拟一个过程使得A →B 为可逆过程，算此过程的热温商，因为熵是状态函数，熵变仅与状态的改变量有关，与途径无关。
本节的重点是说，不可逆过程的熵变不能用热温商计算。
这个结论的作用，请看两道题： 例 1mol 水在373K 和100kPa 向真空蒸发，变成373K 和100kPa 的水蒸气，求系统熵变1S ∆，环境熵变2S ∆，和孤立系统整体熵变S ∆，水的蒸发热为4046kJ/mol 。
解：首先看系统，即：1mol 水在373K 和100kPa →1mol 水蒸气373K 和100kPa ； 模拟一个等温等压可逆相变，那么熵变K J T H S /1091=∆=∆……（6）（TH ∆为热温商）；再看环境的熵变，即 TQ S r -=∆2……（7） 考察水蒸发的热力学能变化值：r Q W U +=∆ (8)显然0=W ，也就是说蒸发过程吸收的热量全部用于增加气体的热力学能，（8）式变为：r Q U =∆ (9))(PV H U ∆-∆=∆ (10)nRT PV =∆)( (11)联立（9）、（10）、（11）得到：K J TnRT H S /7.1002-=+∆-=∆......（12） K J S S S /3.821=∆+∆=∆ (13)（自发过程） 这道题的核心思想是什么呢？就是此过程中水吸热确实吸了r Q ，可用此值计算环境熵变，但是不能用此热量所确定的热温商计算系统的熵变，系统熵变要模拟一可逆过程才可求。
热力学熵函数的探讨热力学熵函数（thermodynamicentropyfunction）是一种用来描述物质的混乱程度的函数，它与物质的原子排列密切相关。
这种混乱程度的函数定义为：热力学熵S等于内能U与温度T的乘积，即S = UT。
热力学熵函数描述了物质系统中不可逆变化的总量，因此它也被称为“不可逆熵”。
二、热力学熵函数的形式和性质热力学熵函数有多种形式，其中最常用的是微分熵，也就是指热力学熵对温度表示为导数的形式，即S = U(dT/T)。
这种函数表示热力学熵的变化随着温度的变化而变化。
另外，热力学熵函数也可以表示为熵函数曲线，即热力学熵随着温度的变化而变化的曲线。
此外，热力学熵函数有三个重要的性质：第一，热力学熵是常数；第二，热力学熵函数可用来表示物质体系的混乱程度；第三，热力学熵函数可用来计算物质体系的热力学熵。
三、热力学熵函数的应用热力学熵函数在物理学和化学学科中有许多应用。
在化学领域，它可以用来表示物质的化学活动，以及物质的热反应和化学反应等热化学反应。
在物理学领域，它用来表示热力作用和自由能变化以及温度变化。
此外，热力学熵函数还可以用来计算物质体系的热量，以及物质开释或吸收热量的情况。
四、热力学熵函数与熵定律熵定律是物理学里最重要的定律之一，也是物质体系最基本的物理规律。
熵定律规定，任何系统的物理熵总是在逐步增大，直到达到最大的平衡状态，这种状态被称为熵的最大化状态。
与熵定律相关的概念就是热力学熵函数。
它可以被用来说明熵定律的作用，表明物质体系的熵增加是一个不可逆过程，并且物质体系的熵一直在增加，直到物质体系的总熵达到最大值，这就是熵的最大化。
五、结论热力学熵函数是一种用来描述物质的混乱程度的函数，它与物质的原子排列密切相关。
它可以用来表示物质体系的混乱程度，以及物质开释或吸收热量的情况，还可以计算物质体系的热量。
热力学熵函数与熵定律有着密切联系，它们联系着物质体系的熵是不可逆的，并且物质体系的总熵一直在增加，最终达到最大值。
热力学中的熵与热力学函数热力学是研究能量转化和能量守恒规律的学科，而熵则是热力学的一个重要概念，用来描述系统的无序程度。
在热力学中，熵是一个基本的物理量，与系统的状态变化密切相关。
本文将探讨熵的概念及其在热力学函数中的应用。
一、熵的概念熵可以理解为系统无序程度的度量，也可以说是系统能量分布的均匀程度。
对于一个孤立系统，其熵是不断增加的，直到达到最大值。
熵的增加意味着系统的无序性增加，系统朝着更加平衡、混乱的状态发展。
熵作为一个状态函数，与系统状态有关，而与过程无关。
根据熵的定义，可以得到下面的熵变公式：ΔS = S_final - S_initial其中，ΔS表示熵的变化，S_final表示系统最终状态的熵，S_initial 表示系统初始状态的熵。
二、熵的计算熵的计算需要根据系统的状态方程和热力学过程的性质进行。
对于简单系统，如理想气体，熵可以通过以下公式进行计算：S = nRlnV - nRlnP + S0其中，S表示熵，n表示物质的摩尔数，R表示气体常数，V表示体积，P表示压力，ln表示自然对数，S0表示常数。
对于复杂系统，如非理想气体或者混合物，熵的计算则需要考虑更多的因素，如化学组成和相对摩尔数等。
这超出了本文的讨论范围。
三、热力学函数与熵的关系热力学函数是描述热力学系统性质的函数，如内能、焓、自由能和吉布斯函数等。
这些函数中，熵在其中起着重要的作用。
在热力学系统中，内能（U）、焓（H）、自由能（F）和吉布斯函数（G）都与熵有着密切的关系。
它们之间的关系由以下公式给出：U = H - PVF = U - TSG = H - TS其中，U表示内能，H表示焓，P表示压强，V表示体积，F表示自由能，T表示温度，S表示熵，G表示吉布斯函数。
熵在这些函数中的作用主要体现在温度和压强的变化过程中。
熵增加意味着系统的无序程度增加，这对应着一种能量向更平均分布的状态转变，也是系统朝着更稳定、更平衡的状态发展。
第二章 热力学第二定律热力学第一定律指出,宏观体系发生的任何过程必须服从能量守恒原理,任何违背这一客观规律的过程都是不能发生的。
但不违背能量守恒原理的过程是否都能自动（即不需外界帮忙，任其自然）发生呢？回答是否定的。
例如，温度不同的两个物体相互接触，热可以自动地由高温物体传向低温物体，直至两物体温度相等，而其逆过程热由低温物体传向高温物体是不能自动发生的；又如，298Ｋ、ｐ压力下，有可能自动发生如下的化学反应 C （金刚石）+O ２（g ）→CO ２（ｇ）Δr Hm＝－393.5kJ.mol －１。
如果在该条件下，令环境供给393.5ｋJ 的热量，由CO ２（g ）分解为金刚石和O ２（g ）则是不能自动发生的。
尽管这些逆过程发生时，并不违背热力学第一定律。
究竟在不违背能量守恒原理的前提下， 什么过程可以发生,什么过程又不可以发生呢？ 热力学第一定律不能给予什么启示，即热力学第一定律只解决了能量守恒、转化以及转化过程中各种能量之间的相互当量关系，但它不能告诉人们过程进行的方向和限度。
是什么因素在决定着过程的方向和限度呢？似乎各类不同的过程有着不同的决定因素。
例如,决定热传导方向和限度的因素是温度Ｔ；决定气体流动方向及限度的因素是压力ｐ；决定水的流动方向和限度的因素是水位ｈ等等。
那么，决定化学变化方向和限度的因素又是什么呢？很有必要找出能判断一切过程方向和限度的共同因素。
因而对于决定变化过程方向和限度的共同因素的探讨，是热力学第二定律所要解决的基本任务——过程的“方向”和“限度”问题。
§2-1自发过程的共同特征 一、自发过程的方向性自发过程：在一定条件下，任其自然，不去管它，能够发生的过程。
（1）热传导：高温→低温，直达相等。
（2）气体的流动：高压→低压，直达相等。
（3）水的流动：高水位→低水位，直达相等。
（4）电能输送：高电位→低电位，直达相等。
可以看出：一切自发过程都具有方向性。
