当前位置：文档之家 › 光波在介质界面上的反射和折射 菲涅耳公式

光波在介质界面上的反射和折射 菲涅耳公式

  • 格式：ppt
  • 大小：301.50 KB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

Fresnel(菲涅尔)公式

Fresnel(菲涅尔)公式

d=z=
2π
λ0
n12 sin2 i1 − n22 ；(3)波矢常数： k2 sin i2 > k2 。
应用：近场光学
15
1.3 反射率和透射率
W1
=
I1σ
cos i1
=
n1 2
ε0 μ0
A1 2 cos i1
W1′ =
I1′σ
cos i1
=
n1 2
ε0 μ0
A1′ 2 cos i1
W2
=
I2σ
cos i2
2.4
2.2
n =1.33 1
n =1
2.0
2
r
r
s
p
1.8
t
t
s
p
1.6
1.4
1.2
i
c
1.0
0.8
0.6
0.4
0.2
i
B
0.0
-0.2 0
10
20
30
40
50
60
i
1
12
全内反射的应用： 1、导波光学 Waveguide / Optical fiber
n 1
n <n , n <n 12 32
n 2
1
Stocks 公式：
A
Ar
Att'
Ar
Arr
Art
At
Atr'
At
Arr + Att′ = A 可知： Art + Atr′ = 0
r2 + tt′ = 1 r + r′ = 0
2
1.2 振幅反射(透射)比 相位跃变(相移) 1、透射比与相位跃变

精选折射和反射定律菲涅耳公式讲义(ppt)

精选折射和反射定律菲涅耳公式讲义(ppt)

(13)
2、公式的另外两种形式
rsE Eri0 0ss n n1 1c co oiiss n n2 2c co ottss
(8)
ts
Er0s Ei0s
n1c2 on1 iscno2 cisots
n1 n2
rp
Er0p Ei0p
n n1 1cco ottss n n2 2ccrpo oiissEEri00(pp12)cco将onss1它ii 们 cc变oon形ss2tt
H ip 界面
ki θi
θr kr
Ers
Hrp
1
O
2
θt kt
Ets
n
H tp
图2
在界面上电场切向分 量连续：
n(E 2E 1)0
Ei0sEr0sEt0s (5)
在界面上磁场的切向分
量连续： n(H 2H 1)0
规定：电场和磁场
的s分量垂直于纸面，
向外为正，向内为负。 H i0 p co i H s r0 p co r s H t0 p co t (s 6)
rsE Eri0 0ss n n1 1c co oiiss n n2 2c co ottss
(8)
ts
Er0s Ei0s
n1c2 on1 iscno2 cisots
(9)
rp
Er0p Ei0p
n1cotsn2cois n1cotsn2cois
(12)
tp
Er0p Ei0p
n1co2n1tscno2cisois
Ei0sEr0sEt0s (5)
rsE Eri0 0ss n n1 1c co oiiss n n2 2c co ottss
(8)
ts

一、 菲涅耳公式(Fresnel formula)

一、 菲涅耳公式(Fresnel formula)

1

4
紫光的散射强度大约是红光的10倍。
4． 偏振性
O z
y p B’
y D A’ B
AP z
x
D’ 实验 自然光入射到散射物质中，观察到：
正侧方（z）线偏振 斜方向（C）部分偏振 对着x方向（x）自然光
解释 用电偶极子次级辐射可解释 实验现象
分解成 +
被微粒散射时，各方向上的振幅可看成以上 两个分振动的合成。 退偏振 线偏振光照射某些气体或液体，从侧向 观察时，散射光变成部分偏振的，称为退偏 振。其机理是介质分子本身是各向异性的。
2．正交棱镜法
研究色散，目的是寻找 n f ( )的函数形式。 正交棱镜装置
三棱镜P1→AH（光谱） P1 P2→A’H’（光谱） n f ( ) ——弯曲光谱的形状。
3．正常色散与反常色散（Normal dispersion and abnormal dispersion）
正常色散曲线的信息
dut余虹一菲涅耳公式fresnelformula第三章光通过各向同性介质及其界面所发生的现象1光在各向同性介质界面上的反射和折射布儒斯特角线偏振光四用反射和折射法获得偏振光布儒斯特定律玻璃片堆要提高反射线偏振光的强度可利用玻璃片堆的多次反射
第三章光通过各向同性介质及其界面所发生的现象 §1 光在各向同性介质界面上的反射和折射 一、 菲涅耳公式（Fresnel formula）
dI Idx dI a Idx I dI d I I 0 a dx a 为吸收系数 I I 0 e a d ，
0
d
a AC ，式中A是一个与浓度无关 稀溶液：
的常量，C为溶液的浓度。
§ 3 光的色散（Dispersion of Light） 1．色散的特点

基础光学第4章光波在界面的反射和折射规律课件

基础光学第4章光波在界面的反射和折射规律课件

无论 n1 n2 或 n1 n2
透射光1’和2’振动方
向相同。即无半波损失。
只要光线2存在，光线1
和2的振动方向总是相
反的，即1和2的光程之
间存在半波损失。
光在多层透明介质界面的反射和折射
n1 < n2< n3 或n3 < n2< n1
时，光线1和2之间的光程
没有半波损失。
当折射率不按顺序排列时，
p
s
n2 n1
t p ts
2n1
n2 n1
入射
反射
约定
n1 < n2 n1 > n2
rp
rs
tp
ts
+
+
+
+
+
约定
实际
实际
+
反射
入射
n1
n2
约定
实际
透射
(a) n1 < n2
n1 < n2 时反射光与入射光振动方向相反
n1 > n2 时反射光与入射光振动方向相同
在任何情况下，透射光的方向和入射光相同
中的多次反射，分别求光从空气（折射率为1.0）正入射到玻
璃上表面，以及光从玻璃下表面射出时的振幅反射率、光强
反射率、振幅透射率和光强透射率。
【解】 正入射： i1 i2 0
n n
2n1
rp 2 1 rs ， t p ts
n2 n1
n2 n1
2
n2 n1
在反射和折射过程中，p, s两个分量的振动是相互独立的
4.2 菲涅尔反射和折射公式
n cos i1 n1 cos i2

菲涅尔方程式

菲涅尔方程式

菲涅尔方程式
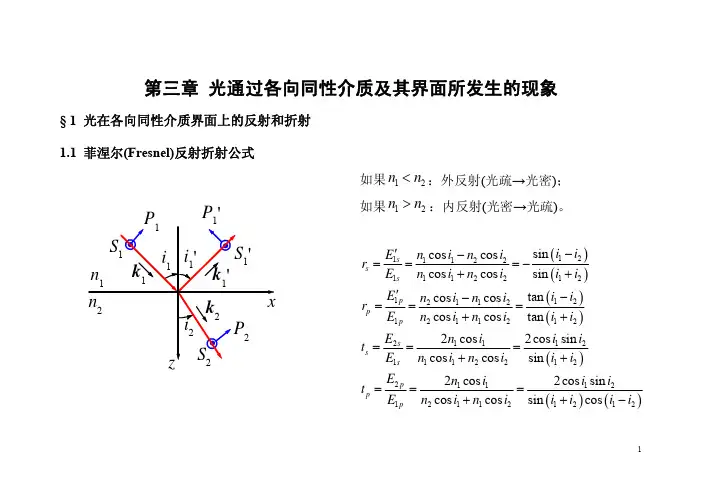
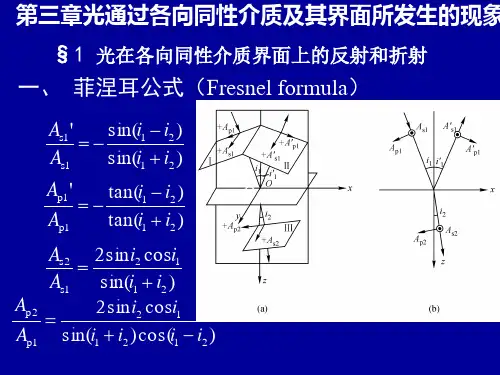
菲涅耳方程式（Fresnel Equations）是用来描述光在两种介质界面上反射和透射的现象和规律的方程式。

它由奥古斯汀·菲涅耳（Augustin-Jean Fresnel）在19世纪提出，并成为光学领域中的重要理论工具。

菲涅耳方程式分为反射方程和透射方程，分别描述了光在界面上的反射和折射（透射）行为。

这些方程式基于电磁波的传播和边界条件，可以通过麦克斯韦方程和边界条件进行推导。

反射方程描述了入射光波在介质界面上的反射行为。

对于垂直入射的光，反射系数（反射光强与入射光强之比）可以通过下述菲涅耳反射方程计算：
r = (n1 - n2) / (n1 + n2)
其中，n1和n2分别是两种介质的折射率，r是反射系数。

透射方程描述了入射光波通过介质界面的折射行为。

同样对于垂直入射的光，透射系数（透射光强与入射光强之比）可以通过下述菲涅耳透射方程计算：
t = 2n1 / (n1 + n2)
其中，n1和n2分别是两种介质的折射率，t是透射系数。

需要注意的是，菲涅耳方程式仅适用于垂直入射的光，并且忽略了光在界面上的散射和吸收行为。

在实际应用中，还需要考虑光的入射角度、极化状态和表面特性等因素，并结合其他衍射、干涉等现象来对界面上的光行为进行更全面的描述。

菲涅耳方程式在材料科学、光学器件设计和表面反射控制等领域中具有广泛的应用，并能解释和预测光在界面上的反射和透射现象。

光波在介质界面上的反射和折射

光波在介质界面上的反射和折射

(3) 应用
3、全反射 、
• 设光波从光密介质射向光疏介质(n 设光波从光密介质射向光疏介质 1>n2)， ， 折射角θ 大于入射角θ 折射角 2 大于入射角 1 。 当 sinθ1 ＝ n2/n1 时 ， θ2 这时折射角沿界面掠过。 为 90o ， 这时折射角沿界面掠过 。 若入射角再 增大， 增大，使sinθ1>n2/n1 ，这时不能定义实数的折 射角。 的入射角θ 称为临界角， 射角 。 使 θ2=90o 的入射角 1 称为临界角 ， 记作 θc即 即
2、反射系数和透射系数
rp =
E0 rp E0ip
n2 cosθ1 − n1 cosθ2 tan(θ1 − θ2 ) = = n2 cosθ1 + n1 cosθ2 tan(θ1 + θ2 )
2n1 cos θ1 2 cos θ1 sinθ 2 = = n2 cos θ1 + n1 cos θ 2 sin(θ1 +θ 2) cos(θ1 −θ 2)
8
2、Fresnel公式－p波 Fresnel公式－ 公式
1、基本关系
e z × ( E0i + E0 r ) = e z × E0t e z × ( H 0i + H 0 r ) = e z × H 0t
H 0ip + H 0 rp＝H t 0 p E0ip cos θi − E0 rp cos θ r＝Et 0 p cos θ t
n2 θ c = arcsin n1
当 θ1≥θc时， 没有折射光， 入射光全部返回 时 没有折射光， 介质1，这个现象为全反射。 介质 ，这个现象为全反射。
16
4、全反射 (1) 定义
当透射波传播方向和法线夹角等于90度时发生的物理现 当透射波传播方向和法线夹角等于90度时发生的物理现 90 发生全反射的最小角度称为临界角( 象。发生全反射的最小角度称为临界角(θc)。

2.10光在电介质表面的反射和折射菲涅尔公式(修正版)

2.10光在电介质表面的反射和折射菲涅尔公式(修正版)

p s

W1'p WW11'sp W1s
Rp Rs
p s
W2 p
WW12ps W1s


cos i2
ccoossii12 cos i1
Tp
Ts
(4) 能量守恒公式：
W1'p W2 p W1p ，W1's W2s W1s
p p 1 ，s s 1
E2s均为复数 E1ss1
E1P E1'


A1P exp(i1p ), E1s
A1' exp(i1' ) E1' p

p1'
A1sEe1x'sps1(' i1s
)
E1' p E2

A1' p exp(i1' p ), A2 exp(i2 )
E1's

A1's
（2）当 i1 iB 时，i1 i2 900
rp

tan( i1 tan( i1
i2 ) i2 )
tan(i1 i2) 0 ，tan(i1 i2 ) 0
rp 0 ，是负的实数
rp rp rp exp(i )
'p(out) ，有相位突变 p(out) 的相位突变如图所示
Rp

cos i2 cos i1
TP
1
，Rs

cos i2 cos i1
Ts
1
rp
2 n2 cos i2 n1 cos i1
tp
2
1
，rs
2 n2 cos i2 n1 cos i1

菲涅尔反射折射公式

菲涅尔反射折射公式

菲涅尔反射折射公式菲涅尔反射折射公式啊，这可是物理学中相当重要的一部分内容呢！咱先来说说啥是菲涅尔反射折射公式。

简单来讲，它就是用来描述光线在不同介质界面上反射和折射时，能量分配情况的一组公式。

这就好比光线是个调皮的小孩子，在不同的“游乐场”（介质）之间穿梭时，它的行为是有规律可循的，而菲涅尔反射折射公式就是这个规律。

比如说，当一束光从空气斜射到玻璃表面时，一部分光会被反射回去，一部分光会折射进玻璃。

那到底反射多少，折射多少呢？这就得靠菲涅尔反射折射公式来算一算啦。

我还记得有一次，在给学生们讲解这个知识点的时候，发生了一件特别有趣的事儿。

那是一个阳光明媚的上午，教室里的光线特别好。

我拿着一块玻璃砖和一个激光笔，准备给学生们做个直观的实验。

我把激光笔的光斜着照在玻璃砖上，然后让学生们观察反射光和折射光的情况。

可是，当我打开激光笔的时候，那束光居然没按照我预想的那样照在玻璃砖上，而是照到了旁边的墙上！全班同学都哄堂大笑，我也有点不好意思。

不过我马上调整了一下，重新让光准确地照在了玻璃砖上。

同学们认真地观察着，眼睛里充满了好奇和探索的欲望。

菲涅尔反射折射公式中的一些参数，像入射角、折射角，还有介质的折射率，它们相互作用，决定了光线的行为。

折射率这个概念也挺有意思，不同的介质有不同的折射率，就像不同的人有不同的性格一样。

比如水的折射率和玻璃的折射率就不一样，所以光在进入水和进入玻璃时的表现也不同。

在实际应用中，菲涅尔反射折射公式可有着大用处呢！比如说在光学仪器的设计中，像照相机的镜头、望远镜的镜片，都得考虑光线的反射和折射，这时候菲涅尔反射折射公式就能派上用场，帮助工程师们设计出更好的产品。

还有在我们日常生活里，你有没有注意过，有时候从水面上看水底的东西，会觉得位置比实际的浅？这其实就是因为光的折射，而菲涅尔反射折射公式就可以解释这个现象。

总之啊，菲涅尔反射折射公式虽然看起来有点复杂，但它其实就像一把钥匙，能帮我们打开了解光的行为的神秘大门。

光波在电介质分界面的反射相位变化matlab

光波在电介质分界面的反射相位变化matlab

光波在电介质分界面的反射相位变化matlab在Matlab 中，可以使用菲涅尔公式绘制介质分界面处折反射光波的幅度、相位变化与入射角的关系。

以下是一段代码示例：```matlab% ********************绘制反射率与相位值随入射角的变化——用于课程作业***********%1. 菲涅尔定律clear,clc,close all;n1 = 1.44;n2 = 1.00; %介质折射率n = n2/n1;theta = linspace(0,pi/2,900);theta_i = theta*180/pi; %电场的反射和透射系数r_E = (cos(theta)-sqrt(abs(n).^2-abs(sin(theta)).^2))./(cos(theta)+sqrt(abs(n).^2-abs (sin(theta)).^2));t_E = 2*cos(theta)./(cos(theta)+sqrt(abs(n).^2-abs(sin(theta)).^2));r_B = (sqrt(abs(n).^2-abs(sin(theta)).^2)-abs(n).^2*cos(theta))./(sqrt(abs(n).^2-abs( sin(theta)).^2)+abs(n).^2*cos(theta));t_B = 2*n*cos(theta)./(abs(n).^2*cos(theta)+sqrt(abs(n).^2-abs(sin(theta)).^2));figure;plot(theta_i,abs(r_E),'--',theta_i,abs(r_B),'-','LineWidth',2);legend('r_E电场','r_B磁场');xlabel('入射角/theta_i'),ylabel('相对反射系数幅度');axis((0 90 0 1));title(['n1 = ',num2str(n1),'n2 = ',num2str(n2),'时反射系数幅度r_E电场。

光学Ts公式

光学Ts公式

光学Ts公式光线经过的第一种介质的折射率为n1,第二种介质折射率为n2,入射角为i1,折射角为i2,R为反射率,T为透射率。

用到光学中的菲涅尔公式。

一般而言,光在两种介质界面发生反射和折射,其反射率和透过率与这两种介质的折射率性质（n1，n2)和入射角度(θ1)有关,与光的偏振状态也有一定的关系。

计算折射角度,即光波在第二种介质的波矢方向可由定律得出：n1×sinθ1=n2×sinθ2计算反射率和透过率就要用到菲涅尔定律,以下讨论不考虑光能吸收的情况,例如金属,若要知道可自己去查比较深入的光学教科书。

1、自然光正入射情况（无偏振特性的光）。

R=（n2-n1)^2/(n2+n1)^2T=1-R此公式最常用,能估算大部分反射率、透过率问题。

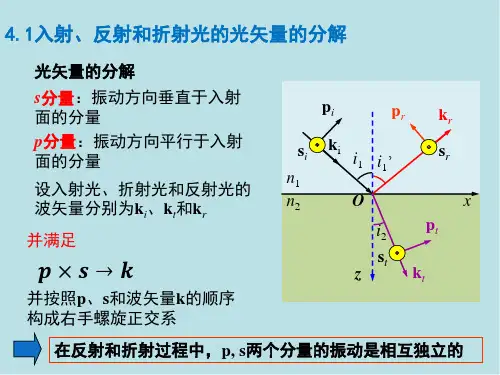
2、偏振光θ1角度入射情况(脚标s代表光波振动方向垂直入射面的偏振光,脚标p代表光波振动方向位于入射面的偏振光）。

Rs=[sin(θ1-θ2)/sin(θ1+θ2)]^2Ts=n2*cosθ2*(2sinθ2cosθ1)^2/[n1*cosθ1*(sin(θ1+θ2))^2]Rp=[tan(θ1-θ2)/tan(θ1+θ2)]^2Tp=n2*cosθ2*(2sinθ2cosθ1)^2/[n1*cosθ1*(sin(θ1+θ2)cos(θ1-θ2))^2能量守恒得到Rs+Ts=1，Rp+Tp=1。

3、任意光波都可分解为S和P光的组合,由数学推导可得到比较精确的结果,不过实际处理时,首先考虑将光波近似为自然光或是偏振光（偏振光是偏振度很高的光）,若为偏振光采用2估算,如果是自然光而且非正入射时候,需要组合得到。

R=(Rs+Rp）/2，P=1-R。

透光率T=It/I0，T是透射光强度（透过比色皿）与入射射光强度（还未过比色皿之前的光强度）之比。

吸光度A=lg（1/T)=-lgT，A是透光率倒数的对数,即透光率的负对数，只有吸光度才与浓度呈正比。

fresnel公式

fresnel公式

fresnel公式Fresnel公式是描述光在两种介质之间传播时发生反射和折射的规律。

它由奥古斯汀·让·菲涅耳在19世纪初提出。

Fresnel公式分为反射和折射两个部分，分别描述了光的入射、反射和透射的振幅和相位之间的关系。

根据Fresnel公式，入射光线在介质界面上会发生一部分反射，另一部分则会折射进入下一个介质。

对于垂直入射的光线，反射系数和折射系数可以按以下公式计算：反射系数R = |(n1 - n2) / (n1 + n2)|^2折射系数T = 1 - R其中，n1和n2分别为上一个介质和下一个介质的折射率。

反射系数表示入射光线被反射的比例，折射系数表示入射光线被折射的比例。

对于非垂直入射的光线，Fresnel公式还包括极化方向的影响。

在这种情况下，入射光线可以分为垂直极化（s极化）和平行极化（p极化）两部分。

对于s极化，反射和折射系数分别为：反射系数Rs = |(n1*cos(θ1) - n2*co s(θ2)) / (n1*cos(θ1) + n2*cos(θ2))|^2折射系数Ts = 1 - Rs其中，θ1和θ2分别为入射角和折射角。

对于p极化，反射和折射系数分别为：反射系数Rp = |(n2*cos(θ1) - n1*cos(θ2)) / (n2*cos(θ1) + n1*cos(θ2))|^2折射系数Tp = 1 - RpFresnel公式在光学领域和光学器件设计中具有广泛应用。

例如，它可以被用来优化反射镜、透镜和光学薄膜的性能，以及研究光在介质中的传播和吸收等现象。

总结来说，Fresnel公式描述了光线在介质界面上的反射和折射行为，它提供了计算反射和折射系数的数学表达式，便于研究光的传播和相位的变化。

光波在介质界面上的反射和折射 菲涅耳公式

光波在介质界面上的反射和折射 菲涅耳公式

m s , p （ 1 2 8 ）
Ers sin(2 1) Eis sin(2 1)
(k ik r)r0 (1 2 1 )
rm
E0rm E0im
(129)
3. 菲涅耳公式 由 （134）式和（133）式消去 Ers，经运算整理得
ts=-n1co2 sn11con s2 c1os2
(135)
rs=-ssiinn((1122))
(134)
( E i s E r s ) n 1 c o s 1 E t s n 2 c o s2( 1 3 3 )
3. 菲涅耳公式
利用类似方法，可以推出 p 分量的反射系数和透射系 数表示式， 这就是著名的菲涅耳公式：
rs
sin(12)=n1cos1n2cos2 sin(12) n1cos1n2cos2
2.1 反射定律和折射定律 (Reflection law and refraction
law)
现假设二介质为均匀、透明、各向同性，分界面为 无穷大的平面，入射、反射和折射光均为平面光波, 其电场表示式为
E l E 0 le － i( lt－ k lr) l i,r,t(1 1 9 )
z
ki 1 2
(ki kr)r0 (121) (ki kt)r0 (122)
kr
B
r
n1 O
n2
ki 分界面
kt
i A
t
C
2.1 反射定律和折射定律 又因为 k n/c ，可将上二式改写为
nisini nrsinr (125) nisini ntsint (126)
这就是介质界面上的反射定律和折射定律，折射定 律又称为斯涅耳（Snell）定律。
n

二、菲涅耳公式表示反射波、折射波与入射波的振幅和位相关

二、菲涅耳公式表示反射波、折射波与入射波的振幅和位相关
W1为入射光能量，由于反射而损失的能量占41%。 为减少光能量损失，近代光学技术普遍采用在光学元 件表面镀增透膜。
小结
光在介质界面上有反射和折射现象：
1）反射或透射光波的振幅、强度、能流可通过菲涅尔
公式进行计算；
2）由菲涅尔公式可知，当平面波在接近正入射或掠入
射，从光疏介质与光密介质的分界面反射时，存在半
rs
菲涅耳公式以入射角表示：
cos 1 n212 sin 2 1 cos 1 n212 sin 2 1 2 cos 1 cos 1 n212 sin 2 1 n212 cos 1 n212 sin 2 1 n212 cos 1 n212 sin 2 1 2n21 cos 1 n212 cos 1 n212 sin 2 1
tp E2 p E1 p 2n1 cos 1 n2 cos 1 n2 cos 2
E1p
p波
振幅透射率
利用关系
n1 sin 1 n2 sin 2
sin(1 2 ) rs sin(1 2 ) 2 cos 1 sin 2 ts sin(1 2 ) tan(1 2 ) rp tan(1 2 ) 2 cos 1 sin 2 tp sin(1 2 ) cos(1 2 )
rs
S波的振幅反射系数
ts
S波的振幅透射系数
A1' s sin(1 2 ) n1 cos1 n2 cos 2 rs A1s sin(1 2 ) n1 cos1 n2 cos 2
A2 s 2 cos1 sin 2 2n1 cos1 ts A1s sin(1 2 ) n1 cos1 n2 cos 2

菲涅尔积分公式

菲涅尔积分公式

菲涅尔积分公式
菲涅尔积分公式是光学和工程学中非常重要的公式之一，它用于描述光在两种不同介质之间反射和折射的过程。

这个公式是由物理学家和数学家奥古斯特·菲涅尔在19世纪初提出的，它基于光的波动理论，描述了光波在两种不同介质之间的传播行为。

菲涅尔积分公式包含两个部分：反射系数和折射系数。

反射系数用于描述光在两种不同介质之间的反射行为，而折射系数用于描述光在两种不同介质之间的折射行为。

这两个系数都与入射角、反射角和折射角有关，同时也与两种介质的折射率有关。

反射系数和折射系数的具体形式如下：
1. 反射系数R = (n2 * sinθi - n1 * sinθt) / (n2 * sinθi + n1 * sinθt)，其中n1 和n2 分别是两种介质的折射率，θi 和θt 分别是入射角和反射角。

2. 折射系数T = 2 * n1 * sinθi / (n2 * sinθt + n1 * sinθi)，其中n1 和n2 分别是两种介质的折射率，θi 和θt 分别是入射角和折射角。

在光学和工程学中，菲涅尔积分公式被广泛应用于计算光在各种不同介质之间的反射和折射行为。

这个公式对于光学设计、成像系统分析、光学仪器制造等领域非常重要。

除了菲涅尔积分公式外，还有许多其他公式和定理用于描述光的行为，例如斯涅尔定律、反射定理、折射定理等。

这些公式和定理都是基于光的波动理论或量子理论，是光学和工程学领域的重要工具。

综上所述，菲涅尔积分公式是一个重要的公式，用于描述光在两种不同介质之间反射和折射的行为。

它基于光的波动理论，包含反射系数和折射系数两个部分，对于光学设计和工程学领域非常重要。

菲涅耳公式

菲涅耳公式
30
扫描隧道光学显微镜
当控制光纤探针在样品表面扫描 时，探针接收到的近场信号经光 纤传输到光学镜头或数字摄像头 进行记录、处理，在逐点还原成 图象等信号。
31
1. 正入射 i1 = 0
rs
n21 n21
1 1
n1 n1
n2 n2
rp
rs
n21 n21
1 1
n2 n2
n1 n1
ts
tp
2 n21 1
2n1 n1 n2
10
2. 布儒斯特角
ib
tan 1
n21
tan 1
n2 n1
i1
ib
rp ib
0 i2
2
ib 称为布儒斯特角
3. 全反射临界角（从光密介质到光疏介质）
n1 n1
E1s E1s
2 2
rs
2
Rp
I1p I1 p
n1 n1
E1p E1 p
2 2
rp
2
光强透射率
Ts
I2s I1s
n2 n1
E2s 2 E1s 2
n2 n1
ts
2
2
Tp
I2 p I1 p
n2 n1
E2 p
2
E1 p
n2 n1
2
tp
6
2.能流反射率 能流透射率
能流比：通过界面上某一面积的入射光、反射光和 折射光的功率之比
光从水中发出，以 不同的入射角射向 空气，所产生的折 射和全反射的情形。
当入射角为
s in c
n2 n1
n21
26
2、倏逝波
全反射的条件： n1 > n2 ,i c 问题：i c 时是否有折射光进入光疏介质？

折射和反射定律、菲涅耳公式

折射和反射定律、菲涅耳公式
1)、当θi≤θc时 此时θt≤90°，可以直接用Fresnel公式来讨论反射波和折射波的性质，分析方法和n1<n2的情形完全相同。
*
图7
rp
rs
tp
ts
|tp|
|ts|
-|rp|
|rs|
n1/n2 =1.5
结论 a)、反射系数rs、rp和n1<n2的情形相反，说明s分量不再存在π位相跃变； b)、sinθc=tanθB=n2/n1，所以必然是θB<θc，说明布儒斯特定律依然有效，同时也说明无论是n1>n2还是n1<n2的情形，布儒斯特定律都成立。 c)、ts和tp均大于1，且随着θi的增大而增大，但是这不意味着透射率T大于1以及T必然随θi的增大而增大。
*
2)、rs始终小于零，其绝对值随着入射角单调增大。根据正方向规定可知，在界面上反射波电场的s分量振动方向始终与入射波s分量相反。
位相跃变(半波损失)
负号写成
在界面上任何一点，反射波s分量与入射波s分量间都有一个π的位相差别。
图4
n2/n1=2.0
位相跃变
这样，位相差π相当于电磁波(光)传播半个波长的距离，所以该现象又可称为半波损失。
即R和T分别是Rs、Rp和Ts、Tp的加权平均。
但是仍然有： R+T=1
*
正入射时，s分量和p分量的差异消失。 若用R0和T0表示此时的反射率和透射率，则有：
利用这两个等式可以估算非正入射但是入射角很小(θi<30°)的反射率和透射率。
2．n1>n2的情形
电场的边界条件
欲使上式对任意的时间t和界面上 均成立，则必然有：
(2)
(1)
可见，时间频率ω是入射电磁波或光波的固有特性，它不因媒质而异，也不会因折射或反射而变化；

光波在介质界面上的反射和折射 菲涅耳公式

光波在介质界面上的反射和折射 菲涅耳公式

在讨论过程中，不计吸收、散射等能量损耗，因此， 入射光能量在反射光和折射光中重新分配，而总能 量保持不变。
2. 3 反射率和透射率 (Reflectivity and transmissivity) 若有一个平面光波以入射角1 斜入射介质分界面， 平面光波的强度为 Ii，则每秒入射到界面上单位面积 的能量为
代入边值关系 n Ei Er n Et ，该式总是成立，故
i r t
( ki k r ) r 0 ( ki k t ) r 0 (120) (121) (122)
2.1 反射定律和折射定律 进一步，根据图所示的几何关系，可得可由（121） 式和（122）式得到
Eis Ers Ets
(131)
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 将 （128）式代入上式，利用（121）式关系，并根据 反射系数定义，得到
sin (1 2 ) rs =sin (1 2 )
Elm E0lm e－i(l t－kl r )
ki sini kr sin r ki sini kt sin t
( ki k r ) r 0 ( ki k t ) r 0
(123) (124)
n1 n2 O
kr ki kt
r
B
分界面
(121) (122)
i
t
A C
2.1 反射定律和折射定律 又因为 k n / c ，可将上二式改写为
Ers sin ( 2 1 ) Eis sin ( 2 1 )
(ki kr ) r 0 (121)
(134)
m s, p
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
ki sini kr sin r ki sini kt sin t
( ki k r ) r 0 ( ki k t ) r 0
(123) (124)
n1 n2 O
kr ki kt
r
B
分界面
(121) (122)
i
t
A C
2.1 反射定律和折射定律 又因为 k n / c ，可将上二式改写为
H ip cos1 H rp cos1 H tp cos 2 (132)
利用
H E ，上式变为
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 再利用折射定律，并由（131）式和（133）式消去 Ets，经整理可得
Ers sin ( 2 1 ) Eis sin ( 2 1 )
sin (1 2 ) rs =sin (1 2 )
(134)
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 利用类似方法，可以推出 p 分量的反射系数和透射系 数表示式， 这就是著名的菲涅耳公式：
O
kr
2
Ers k t
1.s 分量和 p 分量
E p1
H s1
z
1 Hs
E p2 H s2
y
o
E p1
x
2. 反射系数和透射系数 假设介质中的电场矢量为
El E0l e－i(l t－kl r ) l i, r, t ( 127)
其 s 分量和 p 分量表示式为
Elm E0lm e－i(l t－kl r ) m s, p （ 128）
2. 反射系数和透射系数 则定义 s 分量、p 分量的反射系数、透射系数分别为
E0 rm rm E0im E0tm tm E0im
(129) (130)
Elm E0lm e－i(l t－kl r )
m s, p
（ 128）
3. 菲涅耳公式 假设界面上的入射光、反射光和折射光同相位, 根据 电磁场的边界条件及 s 分量、P 分量的正方向规定， 可得 Eis Ers Ets (131) 和
1 2
i r
O
kr
x
界面
t kt
2.1 反射定律和折射定律 r 是界面上任意点的矢径，在上图所示的坐标情况 下，有
r ix jy
z ki n12源自i rOkr
x
界面
t kt
2.1 反射定律和折射定律 根据电磁场的边界条件，可得
i r t
( ki k r ) r 0 ( ki k t ) r 0 (120) (121) (122)
kr
n1 n2 kt O ki 分界面
r
B
i t
A C
1.s 分量和 p 分量 通常把垂直于入射面振动的分量叫做 s 分量，把平 行于入射面振动的分量叫做 p 分量。为讨论方便起 见，规定 s 分量和 p 分量的正方向如图所示。
Erp Ers k i n1 n2 Erp Ers Erp
1 2
Eis Ers Ets
(131)
(Eis Ers )n1cos1 Ets n2 cos 2 (133)
3. 菲涅耳公式 将 （128）式代入上式，利用（121）式关系，并根据 反射系数定义，得到
sin (1 2 ) rs =sin (1 2 )
Elm E0lm e－i(l t－kl r )
代入边值关系 n Ei Er n Et ，该式总是成立，故
i r t
( ki k r ) r 0 ( ki k t ) r 0 (120) (121) (122)
2.1 反射定律和折射定律 进一步，根据图所示的几何关系，可得可由（121） 式和（122）式得到
Ers sin ( 2 1 ) Eis sin ( 2 1 )
(ki kr ) r 0 (121)
(134)
m s, p
（ 128）
E0 rm rm E0 im
(129)
3. 菲涅耳公式 由 （134）式和（133）式消去 Ers，经运算整理得
2n1 cos 1 ts =n1 cos 1 n2 cos 2 (135)
ni sini nr sin r ni sini nt sin t
(125) (126)
这就是介质界面上的反射定律和折射定律，折射定 律又称为斯涅耳（Snell）定律。
2. 2 菲涅耳公式 (Fresnel formula ) 光的电磁理论除了给出描述光在界面上传播方向的 反射定律和折射定律外，还给出入射光、反射光和 折射光之间的振幅、相位关系。
2.1 反射定律和折射定律 (Reflection law and refraction
law)
现假设二介质为均匀、透明、各向同性，分界面为 无穷大的平面，入射、反射和折射光均为平面光波, 其电场表示式为
El E0l e－i (l t－kl r ) l i, r, t (119)
ki z n
①入射光、反射光和折射光具有相同的频率； ②入射光、反射光和折射光均在入射面内，ki、kr 和 kt 波矢关系如图所示。
反射定律和折射定律（三种光传播方向的关系）
El E0l e－i (l t－kl r ) l i, r, t (119)
Ei Ai exp i ki r i t Er Ar exp i k r r r t Et At exp i k t r t t
光波在介质界面上的反射和折射 (The reflection and refraction of light wave in the interface of medium )
由光的电磁理论可知，光在介质界面上的反射和折 射，实质上是光与介质相互作用的结果，因而进行 一般的理论分析非常复杂。在这里，采用简化的处 理方法，不考虑光与介质的微观作用，只根据麦克 斯韦方程组和电磁场的边界条件进行讨论。