信号与系统第七章1郑君里
- 格式:ppt
- 大小:1.05 MB
- 文档页数:24

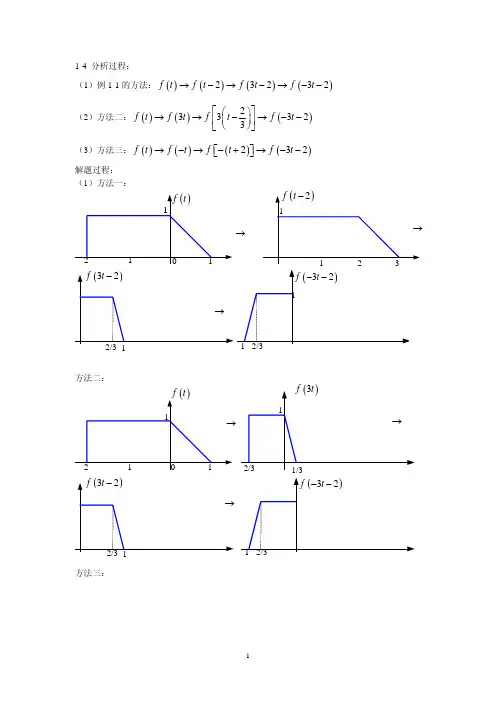




信号与系统复习书中最重要的三大变换几乎都有。
第一章 信号与系统 1、信号的分类 ①连续信号和离散信号 ②周期信号和非周期信号 连续周期信号f (t )满足f (t ) = f (t + m T ), 离散周期信号f(k )满足f (k ) = f (k + m N ),m = 0,±1,±2,…两个周期信号x(t),y(t)的周期分别为T 1和T 2,若其周期之比T 1/T 2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期为T 1和T 2的最小公倍数。
③能量信号和功率信号 ④因果信号和反因果信号 2、信号的基本运算(+ - × ÷) 2.1信号的(+ - × ÷)2.2信号的时间变换运算 (反转、平移和尺度变换) 3、奇异信号3.1 单位冲激函数的性质f (t ) δ(t ) = f (0) δ(t ) , f (t ) δ(t –a) = f (a) δ(t –a)例: 3.2序列δ(k )和ε(k )f (k )δ(k ) = f (0)δ(k ) f (k )δ(k –k 0) = f (k 0)δ(k –k 0)4、系统的分类与性质?d )()4sin(91=-⎰-t t t δπ)0()()(f k k f k =∑∞-∞=δ4.1连续系统和离散系统4.2 动态系统与即时系统4.3 线性系统与非线性系统①线性性质T[a f (·)] = a T[ f (·)](齐次性)T[ f1(·)+ f2(·)] = T[ f1(·)]+T[ f2(·)] (可加性)②当动态系统满足下列三个条件时该系统为线性系统:y(·) = y f(·) + y x(·) = T[{ f(·) }, {0}]+ T[ {0},{x(0)}] (可分解性)T[{a f(·) }, {0}] = a T[{ f(·) }, {0}]T[{f1(t) + f2(t) }, {0}] = T[{ f1(·) }, {0}] + T[{ f2(·) }, {0}](零状态线性) T[{0},{a x1(0) +b x2(0)} ]= aT[{0},{x1(0)}] +bT[{0},{x2(0)}](零输入线性) 4.4时不变系统与时变系统T[{0},f(t -t d)] = y f(t -t d)(时不变性质)直观判断方法:若f (·)前出现变系数,或有反转、展缩变换,则系统为时变系统。



信号与系统课后答案:郑君里第7章简介本文是《信号与系统》课程的第7章课后答案,该章节由著名作者郑君里所撰写。
本章主要介绍了信号与系统的离散傅里叶变换(DFT)和离散时间傅里叶变换(DTFT)。
信号处理是一门研究如何用数学方法描述和处理各种信号的科学。
信号是信息的载体,而系统是对信号进行处理的载体。
离散傅里叶变换和离散时间傅里叶变换是信号与系统理论中最基本的工具之一,它们具有广泛的应用。
理解离散傅里叶变换和离散时间傅里叶变换的原理和性质对于理解信号与系统的基本原理和实际应用非常重要。
第7章课后题答案第1题根据定义,离散傅里叶变换(DFT)的计算公式如下:$$ X(k) = \\sum_{n=0}^{N-1} x(n) \\cdot e^{-j\\frac{2\\pi}{N} nk} $$其中,N表示信号的长度,N(N)表示输入信号的离散采样值,N(N)表示变换结果中的频谱系数。
根据公式,我们可以计算出给定信号的DFT变换。
第2题离散傅里叶变换的逆变换公式如下:$$ x(n) = \\frac{1}{N}\\sum_{k=0}^{N-1} X(k) \\cdot e^{j \\frac{2\\pi}{N} nk} $$逆变换可以将频域表示的信号转换回时域表示。
第3题离散时间傅里叶变换(DTFT)的计算公式如下:$$ X(e^{j\\omega}) = \\sum_{n=-\\infty}^{\\infty} x(n)\\cdot e^{-j\\omega n} $$DTFT是连续的频域表示,它不仅适用于周期信号,也适用于非周期信号。
第4题DTFT的逆变换公式如下:$$ x(n) = \\frac{1}{2\\pi} \\int_{-\\pi}^{\\pi}X(e^{j\\omega}) \\cdot e^{j\\omega n} d\\omega $$逆变换可以将频域表示的信号转换回时域表示。
第5题离散时间傅里叶变换的频谱无法在计算机中实现,因为DTFT变换结果是连续的函数。

12§1.2信号的描述,分类和典型示例(续)•指数信号和正弦信号•奇异信号–斜变信号–单位阶跃信号和符号函数–单位冲激和冲激偶信号正交信号•11(k 实指数信号1—(k 和s 都是实数)•若中的为0 , k 为实数βαj k +=β同时•0 , s ωσs +=ω若中的为,为实数j k则为实指数函数stke t x =)(正弦信号1—取周期复指数的实部•欧拉公式sin(cos()(0ωωφω+++=+t t et j •取实部则为正弦信号)()(00φφj =)cos()(0φω+t A t x 81.3§信号的运算(参考网站绪论的内容)Ee whu edu cn用Flash演示的动态过程§1.4阶跃信号与冲激信号一.奇异信号即本身、其导数或其积分有不连续点的函数。
1.斜变信号2.单位阶跃信号3.符号函数4.单位冲激5.冲激偶信号13信号加窗或取单边t t u t u e t t−−=−)]()([)(0f f(t)f()t(1)突然接入的直流电压()2)突然接通又马上断开电源K负载r(t)r(t 3)r(t 1)r(t 2)r(t-3)-r(t-1)-r(t-2)f(t)1)]2()2()[1()(.101.38−−+−=−t u t u tt f a p 题2....)2()1()()(.+−+−+=t u t u t u t f b )]()([(sin )(.T t u t u t E t f c −−=πT二.单位冲激函数)(t dr )(t du δ=)(t u dt =)(t dt 1.定义:(p17—21))]()([1)(.lim ττδ−−+=t u t u t a 220ττ→)()(t t =δ1=∞dt t limfnn ∞→)(∫∞−fn0=t )(lim ∞→fnn 0≠t 用规则函数脉冲序列的极限来定义)(t Rt ut )(t)(tδtb.Dirac 定义:=)(t δ∫∞=1)(dt t δ00≠t 0=∞t c.利用冲激函数的抽样性∞)()()(00t f dt t t t f =−∫∞δ∞−∫∞−=)0()()(f dt t t f δ∞−)()()(.00t f dt t t t f a =−∫∞−δ1∞)()]([.00t t t t b −=−−δδ)()(.t aat c δδ=)()()()(.000t t t f t t t f d −=−δδt)()(.t dtt u e δ=)()(t u d =∫∞−ττδ+−)(t i c 由于冲激电流的出现,电容两端的电压可以突变;电感电流也可以突变。