信号与系统—第七章习题讲解

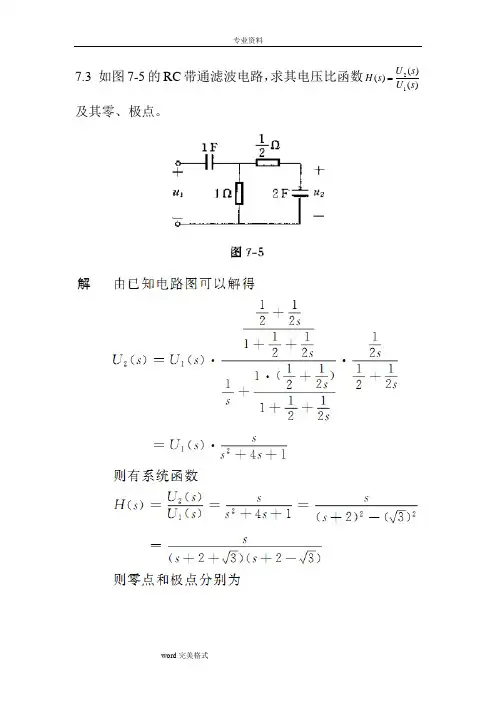
7.3 如图7-5的RC 带通滤波电路，求其电压比函数)()()(12s U s U s H 及其零、极点。

7.7 连续系统a 和b ，其系统函数)(s H 的零点、极点分布如图7-12所示，且已知当∞→s 时，1)(=∞H 。

（1）求出系统函数)(s H 的表达式。

（2）写出幅频响应)(ωj H 的表达式。

7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2，极点在31j ±-，且21)0(=Z ，求R 、L 、C 的值。

7.14 如图7-27所示的离散系统，已知其系统函数的零点在2，极点在-0.6，求各系数a，b。

7.18 图7-29所示连续系统的系数如下，判断该系统是否稳定。

（1）3,210==a a ； （2）3,210-=-=a a ； （3）3,210-==a a 。

7.19 图7-30所示离散系统的系数如下，判断该系统是否稳定。

（1）1,2110-==a a ； （2）1,2110==a a ；（3）1,2110=-=a a 。

7.20 图7-31所示为反馈系统，已知44)(2++=s s ss G ，K 为常数。

为使系统稳定，试确定K 值的范围。

7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y（1） 若该系统为因果系统，求系统的单位序列响应h(k)。

（2） 若该系统为稳定系统，求系统的单位序列响应h(k)，并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。

7.28 求图7-36所示连续系统的系统函数)(sH。

7.30 画出图7-40所示的信号流图，求出其系统函数)(sH。

解(a)由s域系统框图可得系统的信号流图如图7-41(a)。

流图中有一个回路。

其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。

流图中有一个回路。

《信号与系统》（第3版）习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t)表示将f ( t )波形展宽。

](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S RS LS C题1-4图解 系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

第7章 离散时间系统的Z 域分析7.6本章习题全解7.1求下列序列的z 变换，绘出零、极点分布图，并标明收敛域 （1）(1)()0.5()n n n u n δδ+++ （2）5[()(2)]n u n u n --（3）1(1)3n u n ⎛⎫- ⎪⎝⎭（4）1(1)3nu n -⎛⎫-- ⎪⎝⎭（5）0()n n k δ=-∞-∑ （6）0()k n k δ∞=-∑（7）2()n u n （8）2()n u n --（9）2(1)n u n ---- （10）2[()(10)]n u n u n --- （11）0()cos()()(01)n x n Ar n u n r ωφ=+⋅<<解：（1）(1)()0.5()n n n u n δδ+++()5.0,5.01111>-++=-z zz z X（2）5[()(2)]nu n u n --()()()[]0,515251>+=⋅=--=∑∑=-∞-∞=-z z z zn u n u z X n n n n nn（3）1(1)3nu n ⎛⎫- ⎪⎝⎭()()31,131131111313113101>-=--=-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⋅-⎪⎭⎫ ⎝⎛=∑∑∑∞=∞=∞-∞=-z z zz z z n u z X n nn nn nn（4）1(1)3nu n -⎛⎫-- ⎪⎝⎭()()3,313111333131011<-=--=-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛=⋅--⎪⎭⎫ ⎝⎛=∑∑∑∑∞=∞=--∞=-∞-∞=--z z z z z z z z n u z X n nn nn nn n n（5）()n k δ-∑（6）()k n k δ∞=-∑()()()()()n u n n n k n k =+++-+=-∑∞= 210δδδδ()()1,110<-=⎪⎭⎫⎝⎛=⋅=∴∑∑∞=∞-∞=-z z z z zn u z X n nn n（7）2()n u n()()()2,2211220>-=-=⎪⎭⎫ ⎝⎛=⋅=∑∑∞=∞-∞=-z z z zz zn u z X n nn nn（8）2()nu n --()()()()()21,2112220<-===⋅-=∑∑∑∞=-∞=-∞-∞=--z zz z zn u z X n nn nn nn（9）2(1)nu n ----()()()()()()21,2121211122212011<--=+--=+-=-=-=⋅---=∑∑∑∑∞=∞=--∞=-∞-∞=--z zzz z z z zn u z X n nn nn nn nn（10）2[()(10)]nu n u n ---()()()()[]()()∞≤<--=⎪⎭⎫ ⎝⎛=⋅--=-=∞-∞=--∑∑z z z z zn u n u z X n nn nn 0,21212110211090 （11）0()cos()()(01)nx n Ar n u n r ωφ=+⋅<<设()()()()()[]()()()()()()()()()()()22010120101201012010100000cos 21cos cos :1,cos 21cos cos cos 21sin 1sin cos 21cos 1cos :sin sin cos cos sin sin cos cos cos ------------+---=⎪⎭⎫⎝⎛⋅=⋅=>+---=+--⋅-+--⋅=⋅⋅-⋅⋅=⋅-⋅=⋅+=z r r z r z Ar z Y A z X n y Ar n x z z z z z z z z z z z Y n u n n u n n u n n n u n n y n ωωφφωωφφωωφωωφφωφωφωφωφω则又则7.2 求双边序列)(21)(n u n x n⎪⎭⎫⎝⎛=的z 变换，并标明收敛域及绘出零极点图。

信号与系统课后答案：郑君里第7章简介本文是《信号与系统》课程的第7章课后答案，该章节由著名作者郑君里所撰写。

本章主要介绍了信号与系统的离散傅里叶变换（DFT）和离散时间傅里叶变换（DTFT）。

信号处理是一门研究如何用数学方法描述和处理各种信号的科学。

信号是信息的载体，而系统是对信号进行处理的载体。

离散傅里叶变换和离散时间傅里叶变换是信号与系统理论中最基本的工具之一，它们具有广泛的应用。

理解离散傅里叶变换和离散时间傅里叶变换的原理和性质对于理解信号与系统的基本原理和实际应用非常重要。

第7章课后题答案第1题根据定义，离散傅里叶变换（DFT）的计算公式如下：$$ X(k) = \\sum_{n=0}^{N-1} x(n) \\cdot e^{-j\\frac{2\\pi}{N} nk} $$其中，N表示信号的长度，N(N)表示输入信号的离散采样值，N(N)表示变换结果中的频谱系数。

根据公式，我们可以计算出给定信号的DFT变换。

第2题离散傅里叶变换的逆变换公式如下：$$ x(n) = \\frac{1}{N}\\sum_{k=0}^{N-1} X(k) \\cdot e^{j \\frac{2\\pi}{N} nk} $$逆变换可以将频域表示的信号转换回时域表示。

第3题离散时间傅里叶变换（DTFT）的计算公式如下：$$ X(e^{j\\omega}) = \\sum_{n=-\\infty}^{\\infty} x(n)\\cdot e^{-j\\omega n} $$DTFT是连续的频域表示，它不仅适用于周期信号，也适用于非周期信号。

第4题DTFT的逆变换公式如下：$$ x(n) = \\frac{1}{2\\pi} \\int_{-\\pi}^{\\pi}X(e^{j\\omega}) \\cdot e^{j\\omega n} d\\omega $$逆变换可以将频域表示的信号转换回时域表示。

第5题离散时间傅里叶变换的频谱无法在计算机中实现，因为DTFT变换结果是连续的函数。

第七章 习 题7.1 已知频谱包含有直流分量至1000 Hz 分量的连续时间信号f(t)延续1 min ，现对f(t)进行均匀抽样以构成离散信号。

求满足抽样定理的理想抽样的抽样点数。

答案7.2 已知序列}23147212{0k ⋅⋅⋅--==↑,,,,,,f(k)试将其表示成解析（闭合）形式，单位序列组合形式，图形形式和表格形式。

答案7.3 判断以下序列是否为周期序列，若是，则其周期N 为何值？)873cos()( )1(Z k k A k f ∈-=ππ )( )2()8(Z k ek f kj ∈=-π)(cos )( )3(0k kU A k f ω=答案解答：若存在一个整数N ，能使)()(k f N k f =+则)(k f 即为周期为N 的周期序列；若不存在一个周期N ，则)(k f 即为非周期序列。

]87373cos[]8)(73cos[)()1(πππππ-+=-+=+N k A N k A N k f 取,...2,1,0,273==n n N ππ故得372⨯=n N可见当取n=3时，即有N=14。

故)(k f 为一周期序列，其周期为N=14。

)()2(8)8()8(N jk j Nk j ee ek f ππ---+==欲使)(k f 为周期序列，则必须满足πn N28=，即πn N 16=，但由于n 为整数，π不是整数，故N 不可能是整数，因此)(k f 不可能是周期序列。

（3）因)(cos )(0k kU A k f ω=为因果序列。

故为非周期序列。

也可以理解为是在k=0时刻作用于系统的周期序列，其周期为02ωπ=N 。

7.4 求以下序列的差分。

);( ,32)( )1(22k y k k k y ∆+-=求);( ,)()( )2(0k y i f k y ki ∆=∑=求).1()],1([),1()],1([ ),()( )3(-∇-∇-∆-∆=k y k y k y k y k U k y 求答案解答：（1）方法一12]32[3)1(2)1()()1()(22-=+--++-+=-+=∆k k k k k k y k y k y2]12[1)1(2)()1()(2=---+=∆-+∆=∆k k k y k y k y方法二2]32[]3)1(2)1[(23)2(2)2()()1(2)2()]()1([)1()2()()1()]()1([)]([)(2222=+-+++-+-++-+=++-+=-+-+-+=∆-+∆=-+∆=∆∆=∆k k k k k k k y k y k y k y k y k y k y k y k y k y k y k y k y)(...)2()1()0()()( )2(0∑=++++==ki k f f f f i f k y)1()(...)2()1()0()()1(1++++++==+∑+=k f k f f f f i f k y k i 故)1()()1()(+=-+=∆k f k y k y k y)()1()()1()()]1([ )3(k k U k U k y k y k y δ=--=--=-∆。