信号与系统教程燕庆明答案

信号与系统 6.3-1
6.3 线性系统的稳定性
一、稳定的概念
稳定：充要条件是
h(t)
dt
，即H(s)的全部极点
位于S的左半平面；
临界稳定： H(s)在虚轴上有单极点，其余极点均在
S的左半平面；
不稳定： H(s)只要有一个极点位于S的右半平面。
信号与系统 6.3-2
例
图1
二、稳定性判据
信号与系统 6.3-3
必要条件： H( s )的分母多项式
D(s) ansn an-1sn-1 a1s a0
的全部系数非零且均为正实数。 充要条件：对二阶系统，D(s) a2s2 a1s a0 的全部 系数非零且为正实数。 充要条件：对三阶系统，D(s) a3s3 a2s2 a1s a0 的 各项系数全为正，且满足
a1a2 a0a3
信号与系统 6.3-4
例 导弹跟踪系统H (s) Nhomakorabeas3
34.5s2 119.7s 98.1 35.714s2 119.741s 98.1
N (s) D(s)
显然
a1a2 > a0a3
故系统稳定。
练习： 判别稳定性
1. D(s) s2 3s 2 2. D(s) s3 s2 4s 10 3. D(s) s3 4s2 5s 6
end

《信号与系统》（第5版）习题解答燕庆明鲁纯熙高等教育出版社2014年8月目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (24)第5章习题解析 (32)第6章习题解析............................................................................ 错误!未定义书签。

第7章习题解析 (50)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t )表示将f ( t )波形展宽。

] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= t t i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S R S L S C题1-4图解 系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

系数（标量） 乘法器：
积分器：
bn bn -1s -1 b0 s -n N ( s) 将H(s)改写如下： H ( s) -1 -n 1 an -1s a0 s D( s )
F ( s) F ( s) Y ( s) H ( s) F ( s) N ( s) N ( s) X ( s) 其中X ( s) D( s ) D( s )
(a) H ( s)
二、稳定性判据
必要条件： H( s )的分母多项式
D( s) an s n an -1s n -1 a1s a0
的全部系数非零且均为正实数。
充要条件：对三阶系统， ( s) a3s 3 a2 s 2 a1s a0 的 D
各项系数全为正，且满足 a1a2 a0 a3
34.5s 2 119.7 s 98.1 N ( s) H ( s) 3 2 s 35.714s 119.741s 98.1 D( s)
显然 a1a2 > a0a3 故系统稳定。
§6.4 S域分析用于控制系统
一、开环与闭环控制
开环控制：输出的被控对象对输入控制量不产生影
响。 闭环控制： 输出信号的全部或部分返回到输入端 对控制量产生影响。用于反馈自动控制系统。
开环系统
闭环系统
负反馈系统：
H ( s) Y ( s) H1 ( s ) F ( s ) 1 H1 ( s ) H 2 ( s )
反馈系统框图
例
反馈系统示例
对(a)：
H (s) K1K 2 1000 10 1 K1K 2 1 0.099 1000 K1K 2 5 100 9.9 1 K1K 2 1 0.099 500

uc (0 )]
L
diL (t) dt
L[sIL (s)
iL (0 )]
推广： f (t) s2F(s) sf (0) f (0)
信号与系统 5.3-5
4、 积分特性
若 f (t) F(s)
则 t f ( )d F (s)
0
s
表明：一个函数积分后的信号拉氏变换等于原函
数的象函数除以复量s。
信号与系统 5.3-8
拉氏变换的性质表：
名称
时间域
信号与系统 5.3-9
复频域
est0 F (s)
end
2、 延时特性
若 f (t) F(s)
则 f (t t0 ) (t t0 ) F(s)est0
表明：信号延时t0出现时，其拉氏变换是原象函 数乘以与t0有关的指数因子。
信号与系统 5.3-3
例
f (t) (t t0) (t t0)
因
t (t)
1 s2
故
(t
t0 ) (t
t0)
1 s2
应用于系统分析： y(t) f (t) h(t)
Y(s) F(s) H (s)
H (s) h(t)estdt
（S域系统函数）
或者
H (s) Yzs (s) F (s)
由于
s(t)
t
h(t)dt
0
故从积分定理得
S(s) 1 H (s) s
信号与系统 5.3-7
所以阶跃响应为
s(t) 1 H (s) s
如电容上
uc
(t)
uc
(0
)
1 C
t
i( )d
0
则
Uc (s)

2020年北京电子科技学院835电路、信号与系统考研精品资料说明：本套考研资料由本机构多位高分研究生潜心整理编写，2020年考研初试首选资料。

一、重点名校考研真题汇编1．重点名校考研真题汇编①重点名校：电路2010-2018年考研真题汇编（暂无答案）②重点名校：信号与系统2016-2018年考研真题汇编（暂无答案）说明：不同院校真题相似性极高，甚至部分考题完全相同，建议考生备考过程中认真研究其他院校的考研真题。

二、2020年北京电子科技学院835电路、信号与系统考研资料2．李瀚荪《电路分析基础》考研相关资料（1）李瀚荪《电路分析基础》[笔记+课件+提纲]①北京电子科技学院835电路、信号与系统之李瀚荪《电路分析基础》考研复习笔记。

说明：本书重点复习笔记，条理清晰，重难点突出，提高复习效率，基础强化阶段首选资料。

②北京电子科技学院835电路、信号与系统之李瀚荪《电路分析基础》本科生课件。

说明：参考书配套授课PPT课件，条理清晰，内容详尽，版权归属制作教师，本项免费赠送。

③北京电子科技学院835电路、信号与系统之李瀚荪《电路分析基础》复习提纲。

说明：该科目复习重难点提纲，提炼出重难点，有的放矢，提高复习针对性。

（2）李瀚荪《电路分析基础》考研核心题库（含答案）①北京电子科技学院835电路、信号与系统考研核心题库之李瀚荪《电路分析基础》计算题精编。

说明：本题库涵盖了该考研科目常考题型及重点题型，根据历年考研大纲要求，结合考研真题进行的分类汇编并给出了详细答案，针对性强，是考研复习首选资料。

（3）李瀚荪《电路分析基础》考研模拟题[仿真+强化+冲刺]①2020年北京电子科技学院835电路、信号与系统之电路分析基础考研专业课六套仿真模拟题。

说明：严格按照本科目最新专业课真题题型和难度出题，共六套全仿真模拟试题含答案解析。

②2020年北京电子科技学院835电路、信号与系统之电路分析基础考研强化六套模拟题及详细答案解析。

本次课重点

掌握信号的定义 重点学会分析与判断信号的类别与性质
30
电子信息与计算机工程系
习题
a、c、d a、b、c a、b、c
b
d
31
电子信息与计算机工程系
§1.5 系统的概念
系统是指由若干个相互关联、相互作用的事物，按 照一定的规律组成，并且对外具有某种特定功能的 整体。
激励
系统
h（.）


时限信号：若在时间区间 ( t1 , t2 ) 内 f (t) ≠0 ，而在此区间 外 f (t)=0 的信号。
25
电子信息与计算机工程系
§1.3.2 信号分析与处理

时域法 信号表现出一定波形的时间特性，如出现时 间的先后、持续时间的长短、重复周期的大 小及随时间变化的快慢等。 频域法 任意信号在一定条件下总可以分解为许多不 同频率的正弦分量，即具有一定的频率成分 (频谱)。 信号的频谱分析就是研究信号的频率特性。
f (t ) f (t )

T
t
f (t )

T
t
① t 与 t +T 的值相等 周期信号三重含义： ② 延时T，波形相同
③ 波形按T周期重复
22
t
电子信息与计算机工程系
§1.3.1 信号的分类——连续信号与离散信号
连续信号（Continuous-time signals）指在所讨论的时间 模拟信号？ 内，对任意时刻值除若干个不连续点外都有定义的信号。 数字信号？ （ Analog signals ）模拟信号：定义域值域均连续的信号 离散信号（ Discrete-time signals）是指只在某些不连续 规定的时刻有定义，而在其他时刻没有定义的信号。

第6章 系统函数与系统特性 6.1 系统函数与系统模拟 6.2 系统函数的零、极点 6.3 线性系统的稳定性 6.4 S域分析用于控制系统
第7章 离散系统的时域分析 7.1 离散信号与离散系统 7.2 卷积和 Z变换的主要性质 8.3 系统的Z域分析 8.4 系统函数H(Z)与稳定性 8.5 数字滤波器的概念
← 返回总目录 ← 返回上一页 ← 返回本讲第一页 ← 结束本讲放映
目录
第1章 基础概念 1.1 历史的回顾 1.2 应用领域 1.3 信号的概念 1.4 基本信号和信号处理 1.5 系统的概念 1.6 线性时不变系统
第2章 连续系统的时域分析
2.1 系统的微分方程及其响应 2.2 阶跃信号与阶跃响应 2.3 冲激信号与冲激响应 2.4 卷积及其应用 2.5 二阶系统的分析
普通高等教育“十一五”国家级规划教材
（高职高专辅助教学媒体）
燕庆明 主编
高等教育出版社 高等教育电子音像出版社
2007年
前言
“信号与系统”课程是高职高专院校电子信息类各专业的必修课，是“电 路分析”课程后的又一门重要的主干课程。为了帮助教师组织教学，提高教 学效率，我们以教材《信号与系统》（第4版）（燕庆明主编，高等教育出版 社，2007.12）为蓝本，编制了信号与系统电子教案、全书习题解答、 MATLAB仿真和实验指导。参与本教案制作的有燕庆明、鲁纯熙和顾斌杰。
本教案采用PowerPoint制作，应用方便、灵活。其中共设置8章（可讲授 60学时左右）。各校教师可根据实际需要增减有关内容。使用中有何建议可 与我们联系。不当之处，请批评指正。
Tel： (0510)88392227 作者 2007.9
使用说明
运行环境：Office 2000以上。 请安装Office工具中的公式编辑器。 按钮使用： 下列按钮在单击时可超链接到相应幻灯片。

1-2 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为 )()]([)(t f t f T t y == 则 )()()]([111t y t f t f T == )()()]([222t y t f t f T == 不失一般性，设f ( t ) = f 1( t ) + f 2( t )，故有 )()()]([)(21t f t f t f T t y +==)()(21t f t f +≠ 即不满足可加性，为非线性系统。

)]([)()()()]([00000t t f T t t f t t y t t f t t f T -=-=--=-故为时不变系统，综合起来为非线性时不变系统1-3 判断下列方程所表示的系统的性质。

(b) )2()()(3)(2)(-+'=+'+''t f t f t y t y t y (c) )(3)(2)(2)(t f t y t y t t y =+'+''解 (b )是线性常系数微分方程，为线性时不变系统； (c)是线性微分方程，但不是常系数，为线性时变系统。

1-11 由图f(t)画出的f(2t-2)波形)0,2()22()0,2()(),1,5.1()22()1,1()()1,5.1()22()1,1()(),0,1()22()0,0()(的的的的的的的的-→--→--→-→t f t f t f t f t f t f t f t f1-15 计算下列结果)0)3(3(0d )3()()(21d )()3πcos(d )()3πcos()(21200=-≠=-+=-=-⎰⎰⎰-∞∞--t t t t t t c t t t t t b δδδδω时1-17 计算下列各式211])([1d )(d )(d )]()([)()(2)(2)()()]([)()()1()(02222=+='-+='+='+=+-=-=-=-∞+∞--∞+∞--∞+∞------⎰⎰⎰t t t t t t t tt e t t e t t e t t t e b t e t e t t t e dtd dt t d te dt d a δδδδεεδδεεε2-3 设有二阶系统方程 0)(4)(4)(=+'+''t y t y t y 在某起始状态下的0+起始值为2)0(,1)0(='=++y y ，试求零输入响应。

2 2
jt
dt
sin( (

2 )
)

2
Sa (

2
)
2

信号带宽： f
1

2. 冲激函数( t )：
F ( ) (t )e jt dt 1
-
即：
(t ) 1
3. 直流信号：
1 2 ( )
4. 指数信号：
第3章
学习重点：
• • • • • •
信号与系统的频域分析
周期信号分解及其频谱的特点； 非周期信号的频谱及频带宽度； 傅氏变换的性质和应用； 系统函数及不失真传输条件； 取样定理及其应用； 频分复用与时分复用。
傅里叶生平



1768年生于法国 1807年提出“任何周 期信号都可用正弦函 数级数表示” 1829年狄里赫利第一 个给出收敛条件 拉格朗日反对发表 1822年首次发表在 “热的分析理论”一 书中。
对称于坐标纵轴
4 T2 an f (t ) cos ntdt 0 T 0
bn 0
偶函数展开成傅立叶级数后，正弦项为零， 直流分量和余弦项不为零。
（3）f(t)为奇谐函数
T f t f t 2
波形移动T/2后，
与原波形横轴对称。 f(t)的傅氏级数偶次谐波为零 即a0 a2 a4 b2 b4 0
任意信号f(t)可分解为无穷多个幅度为无穷小的 连续指数信号之和。 任意信号f(t)可分解为实函数和虚函数之和。 任意信号f(t)可分解为无穷多个幅度为无穷小的

连续余弦信号之和。
3.3.2 常用信号的频谱函数
1. 门函数：

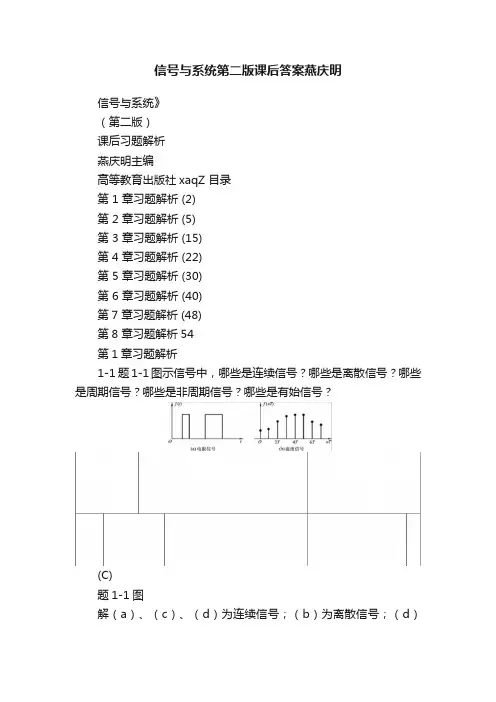
信号与系统第二版课后答案燕庆明信号与系统》（第二版）课后习题解析燕庆明主编高等教育出版社xaqZ 目录第 1 章习题解析 (2)第 2 章习题解析 (5)第 3 章习题解析 (15)第 4 章习题解析 (22)第 5 章习题解析 (30)第 6 章习题解析 (40)第7 章习题解析 (48)第8 章习题解析54第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(C)题1-1图解（a）、（c）、（d）为连续信号；（b）为离散信号；（d）为周期信号；其余为非周期信号；（a）、（b）、（c）为有始（因果）信号。

1- 2 给定题1-2图示信号f（ t ），试画出下列信号的波形。

［提示：f（ 2t ）表示将f（ t ）波形压缩，f?表示将f（ t）波形展宽。

］(a) 2 f( t 2 )(b)f( 2t ) 炸1(c)(d) f( t +1 ) 0r7I题1-2图解以上各函数的波形如图p1-2所示图p1-21-3如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S c ,试写出各系统响应电压与激励电流函数关系的表达式S RS LS c题1-3图解各系统响应与输入的关系可分别表示为U R （t ） R i R （t ）； U L （t ） L d ^ ； U c （t ） 1 t i c （）ddt C1-4 如题1-4图示系统由加法器、积分器和放大量为a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

且 y(t) x(t)dt, x(t) y(t)y (t) f (t) ay(t) y (t) ay(t) f(t) /(-r+D故有即(b)2几-2)何题1-4图系统为反馈联接形式(a)y(t)1- 5已知某系统的输入f( t )与输出y( t )的关系为y( t ) = | f( t )|,试判定该系统是否为线性时不变系统？解设T为系统的运算子，则可以表示为：y(t) T[f(t)] f(t)不失一般性，设f( t ) = f i( t ) + f2( t )，则T[f i(t)] | f i (t) y i(t) ；T[f2(t)] |f2(t) y2(t)故有T[f(t)] | f i (t) f2(t) y(t)显然f i(t) f2(t) f i(t) f2 (t)即不满足可加性，故为非线性时不变系统。

信号与系统燕庆明第三版课后答案【篇一：信号与系统课后习题】t)?tf(t?td),tf(t?t0)?yf(t?t0)?,yf(t?t0)?(t?t0)f(t?t0)。

(3)令g(t)?f(t?t0)，t[g(t)]?g(?t)?f(?t?t0)，tf(t?t0)? yf(t?t0)，yf(t?t0)?f(?t?t0)1.2.已知某系统输入f(t)与输出y(t)的关系为y(t)?f(t)判断该系统是否为线性时不变系统？解:设t为系统运算子，则y(t)可以表示为y(t)?t[f(t)]?f(t),不失一般性，设f(t)?f1(t)?f2(t)t[f1(t)]?f1(t)?y1(t),t[f(t)]?f1(t)?f2(t)?y(t),显然其不相等，即为非线性时不变系统。

df(t)t??f(x)dx(2):[y(t)]2?y(t)?f(t) 1.3判断下列方程所表示系统的性(1):y(t)?0dt（3）：y(t)?2y(t)?3y(t)?f(t)?f(t?2)（4）：y(t)?2ty(t)?2y(t)?3f(t) 线性非线性时不变线性时不变线性时变1.4。

试证明方程y(t)+ay(t)=f(t)所描述的系统为线性系统。

证明：不失一般性，设输入有两个分量，且f1(t)→y1(t),f2(t)→y2(t) 则有y1(t)+ay1(t)=f1（t)，y2(t)+ay2(t)=f2(t) 相加得y1+ay1(t)+y2(t)+ay2(t)=f1(t)+f2(t) 即d[y1(t)+y2(t)]+a[y1(t)+y2(t)] dtt)+y2(t)即满足可加性，齐次性是显然的。

故系统为线性的。

1.5。

证明1.4满足时不变性。

证明将方程中的t换为t-t0,t0为常数。

即y(t-t0)+ay(t-t0)=f(t-t0) 由链导发则，有dy(t?t0)? dtd(t?t0)dy(t?t0)d(t?t0)dy(t?t0)dy(t?t0)?1从而又因t0为常数，故所以有 ??dtd(t?t0)dtdtd(t?t0)dy(t?t0)?ay(t?t0)?f(t?t0)即满足时不变性f(t-t0)→y(t-t0) dty(t)?y(t?t0)f(t)?f(t??t)?所以?t?tlimf(t)?f(t??t)limy(t)?f(t?t0)既有 f(t)?y(t) ??t?0?t?0?t?t1.7 若有线性时不变系统的方程为y(t)+ay(t)=f(t)在非零f(t)作用下其响应y(t)=1-e-t,试求方程y(t)+ay(t)=2f(t)+f(t)的响应。

1
计算：
2.1 设有如下函数 f( t )，试分别画出它们的波形。 (a) f( t ) = 2( t 1 ) 2( t 2 ) (b) f( t ) = sint[( t ) ( t 6 )]
2-2 试用阶跃函数的组合表示题 2-4 图所示信号。 解(a) f( t ) = ( t ) 2( t 1 ) + ( t 2 )

f
(t
t0 ) 即满足时不变性
f(t-t0)→y(t-t0)
1.6.试一般性地证明线性时不变系统具有微分特性。
证明 设 f(t)→y(t),则 f(t-Δt)→y(t-Δt)又因为 f (t) f (t t) y(t) y(t t0 ) 所以
t
t
lim f (t) f (t t) lim y(t) f (t t0 ) 既有 f '(t) y'(t)
h(t) x1(t) [ (t) (t)] (t) 2e3t (t) 阶跃响应
s(t)
t
h( )d

1 (1
2e 3t
) (t)
0
3
3.6LTI系统的冲激响应如图(a),若输入信号f (t)如图（b)所示三角波，求零状态响应？
本题用图形扫描计算卷积即y(t) h(t) f (t) 0(t 0),
(7)=2 t


3-1 如图 2-1 所示系统，试以 uC( t )为输出列出其微分方程。
解 由图示，有
iL

uC R
C
duC dt
又 iL

1 L
t
0(uS uC )dt 故
1 L

《信号与系统教程》教学指导书--燕庆明教育科学“十五”国家规划课题研究成果《信号与系统教程》教学指导书燕庆明高等教育出版社书书书内容提要本书是与燕庆明主编《信号与系统教程》相配套的教学指导书。

书中明确了主教材各章的教学目标和教学重点,并对重点给予指导。

内容精炼,例题丰富。

书中除了对全书的习题进行解析外,还编写了!套模拟试题,为学生自学检测提供帮助。

本书适合于高等学校电子信息类专业的教师和学生作为“信号与系统”课程的教学参考书和学习指导书。

" 图书在版编目(!"#)数据"《信号与系统教程》教学指导书#燕庆明$ ?北京:高等教育出版社, %&&’ %" *+,-/&0 /&’&1 /." 信?" 燕?" 信号系统 /高等学校 /! " #教学参考资料" 2-3$4$" 中国版本图书馆 5*6数据核字(%&&’)第&331’号出版发行" 高等教育出版社" " " " " " " " 购书热线" && /40&101!!社" " 址" 北京市西城区德外大街0号免费咨询" !&& /!& /&13!邮政编码" &&& 网" " 址" 7889:# #::: 7;9 ; ?总" " 机" && /!%&%!!33 " " " " " 7889:# #::: 7;9 @A ?经" " 销" 新华书店北京发行所印" " 刷"开" " 本" .!. B34&" #4 版" " 次" " " 年" 月第版印" " 张" 3$1 印" " 次" " " 年" 月第次印刷字" " 数" .& &&& 定" " 价" % 1&元本书如有缺页、倒页、脱页等质量问题,请到所购图书销售部门联系调换。

2 1 rad / s T 1 T F0 a0 f (t )dt 0 T 0

0
T 2
Ae jn1t dt Ae jn1t dt
T 2 0
1 Fn T

T 2 T 2
T 1 2 jn1t jn1t 2 f (t )e dt Ae dt Ae jn t dt 0 T 0
3.2 周期信号的频谱

3.2.1 周期信号频谱的特点
4A 1 1 f (t ) (sin 1t sin 31t sin 51t ) π 3 5
4A π 1 π cos( t ) cos( 3 t ) 1 1 π 2 3 2
2 1 T
4 A cos n1t T n1
T 2 0
图2
4A nπ (n 1, 3, 5,)
2 A (1 cos n ) nπ
0
(n 2, 4, 6,)
所以f(t)的傅里叶级数为
f (t ) 4A 1 1 (sin 1t sin 31t sin 51t ) π 3 5
A jn t 1 A A jn e [e 1] [cos n 1] 0 jn jn jn 2A j n 0 ( n 1, 3, 5, ) ( n 2, 4, )
从而复系数Fn的模和相位分别为
2A Fn ( n 1, 3, 5, ) n o 90 ( n 1,3,5, ) n o ( n 1, 3, 5, ) 90
周期信号分解为三角级数31锯齿波的三角级数合成周期信号是定义在区间上每隔一定周期t按相同规律重复变化的信号它们可一般地表示当周期信号ft满足狄里赫利条件时则可用傅里叶级数表示为coscoscos3sinsin1在一个周期内只有有限个极大值和极小值且只有有限个第一类不连续点

信号与系统 6.2-10
例 y(n) a1 y(n 1) a2 y(n 2) b0 f (n) b1 f (n 1) b2 f (n 2) 由上式的关系可画出如图8所示的模拟框图。
图8
end
信号与系统 6.2-1
6.2 离散信号与离散系统
一、离散时间信号
它是 仅在离散时刻有定义的信号。 表示气温、压力、流量、高度、电压、 电流等在离散时刻的数据。便于计算机处理 和控制。常用离散信号如下：
信号与系统 6.2-2
图1 常用离散信号
➢ 单位函数（序列）：
1 ( n ) =
0
➢ 单位阶跃序列：
二、离散时间系统
信号与系统 6.2-6
差分方程：微分方程的离散化。对一阶RC电路
duc (t) dt
1 RC
uc (t)
1 RC
us (t)
对上式取样，得
uc[(n
1)T ] T
uc (nT )
1 RC
uc (nT )
1 RC
us (nT )
令T = 1，即
uc (n 1) auc (n) bus (n) 梯形网络的节点电位方程（见图5）
u(n 1) u(n) u(n) u(n) u(n 1)
R
R
R
信号与系统 6.2-7图5 梯电阻网络根据KCL，有
u(n 1) u(n) u(n) u(n) u(n 1)
R
aR
R
整理可得
au(n 1) au(n 1) (2a 1)u(n) 0
信号与系统 6.2-8
1 ( n ) =
0
➢ 指数序列：
(n=0) (n0)
(n0) (n<0)