电子教案《信号与系统》(第四版_燕庆明)(含习题解答)6.4

信号与系统 6.3-1
6.3 线性系统的稳定性
一、稳定的概念
稳定：充要条件是
h(t)
dt
，即H(s)的全部极点
位于S的左半平面；
临界稳定： H(s)在虚轴上有单极点，其余极点均在
S的左半平面；
不稳定： H(s)只要有一个极点位于S的右半平面。
信号与系统 6.3-2
例
图1
二、稳定性判据
信号与系统 6.3-3
必要条件： H( s )的分母多项式
D(s) ansn an-1sn-1 a1s a0
的全部系数非零且均为正实数。 充要条件：对二阶系统，D(s) a2s2 a1s a0 的全部 系数非零且为正实数。 充要条件：对三阶系统，D(s) a3s3 a2s2 a1s a0 的 各项系数全为正，且满足
a1a2 a0a3
信号与系统 6.3-4
例 导弹跟踪系统H (s) Nhomakorabeas3
34.5s2 119.7s 98.1 35.714s2 119.741s 98.1
N (s) D(s)
显然
a1a2 > a0a3
故系统稳定。
练习： 判别稳定性
1. D(s) s2 3s 2 2. D(s) s3 s2 4s 10 3. D(s) s3 4s2 5s 6
end

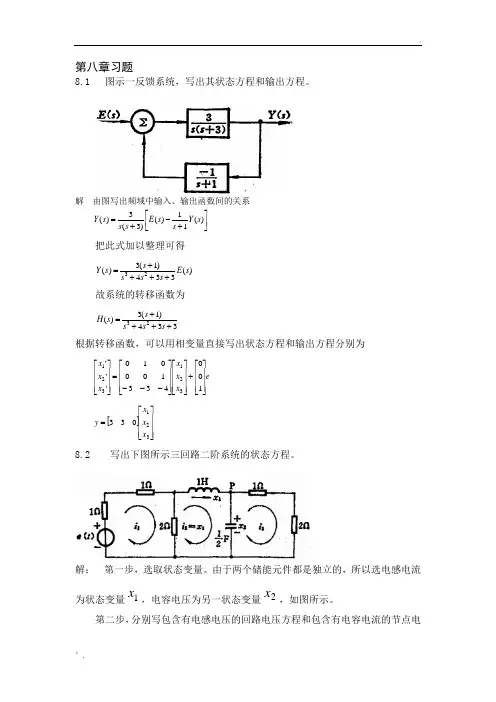
第八章习题8.1 图示一反馈系统，写出其状态方程和输出方程。

解由图写出频域中输入、输出函数间的关系⎥⎦⎤⎢⎣⎡+-+=)(11)()3(3)(sYssEsssY把此式加以整理可得)(334)1(3)(23sEsssssY++++=故系统的转移函数为334)1(3)(23++++=sssssH根据转移函数，可以用相变量直接写出状态方程和输出方程分别为exxxxxx⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡143311'''321321[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=32133xxxy8.2 写出下图所示三回路二阶系统的状态方程。

解：第一步，选取状态变量。

由于两个储能元件都是独立的，所以选电感电流为状态变量1x，电容电压为另一状态变量2x，如图所示。

第二步，分别写包含有电感电压的回路电压方程和包含有电容电流的节点电流方程。

根据第二个回路的回路方程，并代入元件参数，则有112122'ixxx+--=312'21ixx-=第三步，上两式中1i和3i不是状态变量，要把它们表为状态变量。

由第一个回路有1124xie-=，即112141xei+=由第三个回路有323ix=，即2331xi=把1i和3i分别代入第二步中两式，并经整理，最后得所求状态方程为exxx21'211+--=212322'xxx-=或记成矩阵形式8.3 图示一小信号谐振放大器的等效电路，这里的激励函数)(t e是一压控电流源，输出电压)(t y由耦合电路的电阻L R上取得。

要求写出此电路的状态方程和输出方程。

解：第一步，选状态变量。

因为电感电流和电容电压等三个变量都是独立的，所以选回路电感L中的电流1x、回路电容C上的电压2x、耦合电容c C上的电压3x为状态变量。

第二步，分别写回路方程或节点方程。

由RLC回路有211'xRxLx=+eixxCCx rc-=+++132''RL c i x C ='3第三步，消去非状态变量。

专业课习题解析课程xxxxxx大学844信号与系统专业课习题解析课程第1讲第一章信号与系统（一）专业课习题解析课程第2讲第一章 信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f =（7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为（2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)tf=r)(sin(t（7）)f kε=t)(2(k（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=kkkkfεεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的辯达式。

1-4 写出图1-4所示各序列的闭合形式辯达式。

信号与系统教程燕庆明答案【篇一：信号与系统课后习题】t)?tf(t?td),tf(t?t0)?yf(t?t0)?,yf(t?t0)?(t?t0)f(t?t0)。

(3)令g(t)?f(t?t0)，t[g(t)]?g(?t)?f(?t?t0)，tf(t?t0)? yf(t?t0)，yf(t?t0)?f(?t?t0)1.2.已知某系统输入f(t)与输出y(t)的关系为y(t)?f(t)判断该系统是否为线性时不变系统？解:设t为系统运算子，则y(t)可以表示为y(t)?t[f(t)]?f(t),不失一般性，设f(t)?f1(t)?f2(t)t[f1(t)]?f1(t)?y1(t),t[f(t)]?f1(t)?f2(t)?y(t),显然其不相等，即为非线性时不变系统。

df(t)tf(x)dx(2):[y(t)]2?y(t)?f(t) 1.3判断下列方程所表示系统的性(1):y(t)?0dt（3）：y(t)?2y(t)?3y(t)?f(t)?f(t?2)（4）：y(t)?2ty(t)?2y(t)?3f(t) 线性非线性时不变线性时不变线性时变1.4。

试证明方程y(t)+ay(t)=f(t)所描述的系统为线性系统。

证明：不失一般性，设输入有两个分量，且f1(t)→y1(t),f2(t)→y2(t) 则有y1(t)+ay1(t)=f1（t)，y2(t)+ay2(t)=f2(t) 相加得y1+ay1(t)+y2(t)+ay2(t)=f1(t)+f2(t) 即d[y1(t)+y2(t)]+a[y1(t)+y2(t)] dt=f1(t)+f2(t）可见f1(t)+f2(t)→y1(t)+y2(t)即满足可加性，齐次性是显然的。

故系统为线性的。

1.5。

证明1.4满足时不变性。

证明将方程中的t换为t-t0,t0为常数。

即y(t-t0)+ay(t-t0)=f(t-t0) 由链导发则，有dy(t?t0)dtd(t?t0)dy(t?t0)d(t?t0)dy(t?t0)dy(t?t0)1从而又因t0为常数，故所以有 ??dtd(t?t0)dtdtd(t?t0)dy(t?t0)ay(tt0)f(tt0)即满足时不变性f(t-t0)→y(t-t0) dty(t)?y(t?t0)f(t)?f(t??t)?所以ttlimf(t)?f(t??t)limy(t)?f(t?t0)既有 f(t)?y(t) ?t0t0tt1.7 若有线性时不变系统的方程为y(t)+ay(t)=f(t)在非零f(t)作用下其响应y(t)=1-e-t,试求方程y(t)+ay(t)=2f(t)+f(t)的响应。

信号与系统授课计划课程名称：信号与系统课程类别：专业课总课时：60-72教材（主编、出版社、出版日期）：《信号与系统》、郑君里、高等教育出版社、2003.5第一章绪论（8-10课时）本章是信号与系统课程的总论，包括信号与系统课程概述和一些基本概念，简单来说就是要讲清楚什么是信号、什么是系统、以及信号与系统之间是什么关系的问题。

主要内容包括：信号与系统课程概述、信号与系统课程的主要内容、信号的定义及常见信号介绍以及信号的运算、系统的定义与分类以及系统的分析方法介绍等。

本章内容是全书内容的浓缩、是基础、是引言，所以非常重要。

一、主要知识点如下：1、信号与系统课程概述主要包括：（1）信号与系统课程的产生与发展（2）信号与系统课程与其他课程的联系（3）信号与系统的应用领域2、信号的定义与分类、信号的运算主要包括：（1）信号的定义与分类（2）信号的运算3、系统的定义、分类及分析方法主要包括：（1）系统的定义及分类（2）线性时不变系统四大特性及判断方法二、本章知识重难点分析1、信号的定义及分类是重点，其中关于周期信号的定义及信号周期的计算是难点，同样关于连续时间信号与离散时间信号的定义与区别也是难点。

2、几种特殊信号的定义是本课程的重点内容，包括单位阶跃信号、单位冲激信号的定义与运算。

其中单位阶跃信号与单位冲激信号的定义与性质是难点。

3、信号的运算也是本章知识的重点内容，特别是信号直流分量与交流分量、信号奇分量与偶分量等的分解运算，信号的尺度、位移、反折运算等。

4、系统的定义及分类是重点5、线性时不变系统的定义及四大特性，其中四大特性（微积分、时不变、线性、因果性）的定义与判断是难点，特别是线性性是非常重要的内容。

6、线性时不变系统的分析方法是本章的重点7、系统的描述方法，框图与方程，框图与方程之间的关系与转换方法，其中框图与方程之间的转换关系是难点。

三、本章知识点课时安排1、信号与系统课程概述（2课时）2、信号的定义与分类、信号的运算（3课时）3、系统的定义、分类及分析方法（3课时）第二章连续时间系统的时域分析（6-8课时）LTI连续系统的时域分析过程可以理解为建立并求解线性微分方程，因其分析过程涉及的函数变量均为时间t，故称为时域分析法。

即
故f(t)与{c0, c1, …, cN}一一对应。
7
3.3 设
第3章 连续信号与系统的频域分析
试问函数组｛ξ1(t),ξ2(t),ξ3(t),ξ4(t)｝在(0，4)区间上是否 为正交函数组，是否为归一化正交函数组，是否为完备正交函 数组，并用它们的线性组合精确地表示题图 3.2 所示函数f(t)。
题图 3.10
51
第3章 连续信号与系统的频域分析 52
第3章 连续信号与系统的频域分析 53
第3章 连续信号与系统的频域分析 54
第3章 连续信号与系统的频域分析 55
第3章 连续信号与系统的频域分析 56
第3章 连续信号与系统的频域分析 57
第3章 连续信号与系统的频域分析
题解图 3.19-1
8
第3章 连续信号与系统的频域分析
题图 3.2
9
第3章 连续信号与系统的频域分析
解 据ξi(t)的定义式可知ξ1(t)、ξ2(t)、ξ3(t)、ξ4(t)的波形如题 解图3.3-1所示。
题解图 3.3-1
10
不难得到：
第3章 连续信号与系统的频域分析
可知在(0,4)区间ξi(t)为归一化正交函数集,从而有
激励信号为f(t)。试证明系统的响应y(t)=－f(t)。
69
证 因为
第3章 连续信号与系统的频域分析
所以
即
70
系统函数
第3章 连续信号与系统的频域分析
故
因此
71
第3章 连续信号与系统的频域分析
3.23 设f(t)的傅里叶变换为F(jω)，且 试在K≥ωm条件下化简下式：
72
第3章 连续信号与系统的频域分析 73
107

第5-3页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
一、从傅里叶变换到拉普拉斯变换
有些函数不满足绝对可积条件，求解傅里叶变换困难。 为此，可用一衰减因子e-t(为实常数）乘信号f(t) ，适当 选取的值，使乘积信号f(t) e-t当t∞时信号幅度趋近于 0 ，从而使f(t) e-t的傅里叶变换存在。
0
β
σ
第5-7页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
例3 双边信号求其拉普拉斯变换。
e t , t 0 f 3 (t ) f1 (t ) f 2 (t ) t e , t 0
求其拉普拉斯变换。
解 其双边拉普拉斯变换 F (s)=F (s)+F (s) b b1 b2
第5-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
四、常见函数的单边拉普拉斯变换
1. (t ) 1, 2.( t) 或1 3. ( t ) s, 4. 指数信号e
1
s
, 0

1 s s0
s0t

令s0 0
第5-12页
(t )
■
1
s
, 0
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
4.1 拉普拉斯变换
五、单边拉氏变换与傅里叶变换的关系
F ( s) f (t ) e st d t
0
Re[s]>0
F (j ) f (t ) e

(t+ 3 ) *(t5 )=
也可以利用迟延性质计算该卷积。因为
(t) *(t)=t(t)
f1(tt1) *f2(tt2)=f(tt1t2)
故对本题，有
(t+ 3 ) *(t5 )=(t+ 35)(t+ 35)=(t2)(t2)
两种方法结果一致。
(c)tet(t)*(t)= [tet(t)]= (ettet)(t)
题2-1图
解由图示，有
又
故
从而得
2-2设有二阶系统方程
在某起始状态下的0+起始值为
试求零输入响应。
解由特征方程
2+ 4+ 4 =0
得1=2=2
则零输入响应形式为
由于
yzi( 0+) =A1= 1
2A1+A2= 2
所以
A2= 4
故有
2-3设有如下函数f(t)，试分别画出它们的波形。
(a)f(t) = 2(t1 )2(t2 )
第5章
5-1求下列函数的单边拉氏变换。
(1)
(2)
(3)
解(1)
(2)
(3)
5-2求下列题5-2图示各信号的拉氏变换。
题5-2图
解(a)因为
而
故
(b)因为
又因为
故有
5-3利用微积分性质，求题5-3所示信号的拉氏变换。
题5-3图
解先对f(t)求导，则
故对应的变换
所以
5-4用部分分式法求下列象函数的拉氏反变换。
它们的频谱变化分别如图p4-8所示，设C>2。
图p4-8
4-9如题4-9图所示系统，设输入信号f(t)的频谱F()和系统特性H1()、H2()均给定，试画出y(t)的频谱。

第6章 系统函数与系统特性 6.1 系统函数与系统模拟 6.2 系统函数的零、极点 6.3 线性系统的稳定性 6.4 S域分析用于控制系统
第7章 离散系统的时域分析 7.1 离散信号与离散系统 7.2 卷积和 Z变换的主要性质 8.3 系统的Z域分析 8.4 系统函数H(Z)与稳定性 8.5 数字滤波器的概念
← 返回总目录 ← 返回上一页 ← 返回本讲第一页 ← 结束本讲放映
目录
第1章 基础概念 1.1 历史的回顾 1.2 应用领域 1.3 信号的概念 1.4 基本信号和信号处理 1.5 系统的概念 1.6 线性时不变系统
第2章 连续系统的时域分析
2.1 系统的微分方程及其响应 2.2 阶跃信号与阶跃响应 2.3 冲激信号与冲激响应 2.4 卷积及其应用 2.5 二阶系统的分析
普通高等教育“十一五”国家级规划教材
（高职高专辅助教学媒体）
燕庆明 主编
高等教育出版社 高等教育电子音像出版社
2007年
前言
“信号与系统”课程是高职高专院校电子信息类各专业的必修课，是“电 路分析”课程后的又一门重要的主干课程。为了帮助教师组织教学，提高教 学效率，我们以教材《信号与系统》（第4版）（燕庆明主编，高等教育出版 社，2007.12）为蓝本，编制了信号与系统电子教案、全书习题解答、 MATLAB仿真和实验指导。参与本教案制作的有燕庆明、鲁纯熙和顾斌杰。
本教案采用PowerPoint制作，应用方便、灵活。其中共设置8章（可讲授 60学时左右）。各校教师可根据实际需要增减有关内容。使用中有何建议可 与我们联系。不当之处，请批评指正。
Tel： (0510)88392227 作者 2007.9
使用说明
运行环境：Office 2000以上。 请安装Office工具中的公式编辑器。 按钮使用： 下列按钮在单击时可超链接到相应幻灯片。

1
计算：
2.1 设有如下函数 f( t )，试分别画出它们的波形。 (a) f( t ) = 2( t 1 ) 2( t 2 ) (b) f( t ) = sint[( t ) ( t 6 )]
2-2 试用阶跃函数的组合表示题 2-4 图所示信号。 解(a) f( t ) = ( t ) 2( t 1 ) + ( t 2 )

f
(t
t0 ) 即满足时不变性
f(t-t0)→y(t-t0)
1.6.试一般性地证明线性时不变系统具有微分特性。
证明 设 f(t)→y(t),则 f(t-Δt)→y(t-Δt)又因为 f (t) f (t t) y(t) y(t t0 ) 所以
t
t
lim f (t) f (t t) lim y(t) f (t t0 ) 既有 f '(t) y'(t)
h(t) x1(t) [ (t) (t)] (t) 2e3t (t) 阶跃响应
s(t)
t
h( )d

1 (1
2e 3t
) (t)
0
3
3.6LTI系统的冲激响应如图(a),若输入信号f (t)如图（b)所示三角波，求零状态响应？
本题用图形扫描计算卷积即y(t) h(t) f (t) 0(t 0),
(7)=2 t


3-1 如图 2-1 所示系统，试以 uC( t )为输出列出其微分方程。
解 由图示，有
iL

uC R
C
duC dt
又 iL

1 L
t
0(uS uC )dt 故
1 L

《信号与系统教程》教学指导书--燕庆明教育科学“十五”国家规划课题研究成果《信号与系统教程》教学指导书燕庆明高等教育出版社书书书内容提要本书是与燕庆明主编《信号与系统教程》相配套的教学指导书。

书中明确了主教材各章的教学目标和教学重点,并对重点给予指导。

内容精炼,例题丰富。

书中除了对全书的习题进行解析外,还编写了!套模拟试题,为学生自学检测提供帮助。

本书适合于高等学校电子信息类专业的教师和学生作为“信号与系统”课程的教学参考书和学习指导书。

" 图书在版编目(!"#)数据"《信号与系统教程》教学指导书#燕庆明$ ?北京:高等教育出版社, %&&’ %" *+,-/&0 /&’&1 /." 信?" 燕?" 信号系统 /高等学校 /! " #教学参考资料" 2-3$4$" 中国版本图书馆 5*6数据核字(%&&’)第&331’号出版发行" 高等教育出版社" " " " " " " " 购书热线" && /40&101!!社" " 址" 北京市西城区德外大街0号免费咨询" !&& /!& /&13!邮政编码" &&& 网" " 址" 7889:# #::: 7;9 ; ?总" " 机" && /!%&%!!33 " " " " " 7889:# #::: 7;9 @A ?经" " 销" 新华书店北京发行所印" " 刷"开" " 本" .!. B34&" #4 版" " 次" " " 年" 月第版印" " 张" 3$1 印" " 次" " " 年" 月第次印刷字" " 数" .& &&& 定" " 价" % 1&元本书如有缺页、倒页、脱页等质量问题,请到所购图书销售部门联系调换。

5 t(ms)
0
10
2负逻辑
数字信号是一种二值信号，用两个电平（高电平和低电 平）分别来表示两个逻辑值（逻辑1和逻辑0）。 有两种逻辑体制： 正逻辑体制规定：高电平为逻辑1，低电平为逻辑0。 负逻辑体制规定：低电平为逻辑1，高电平为逻辑0。
下图为采用正逻辑体制所表的示逻辑信号：
（二）、逻辑函数的表示方法
1．真值表——将输入逻辑变量的各种可能取值和相应的函数值排列 在一起而组成的表格。 2．函数表达式——由逻辑变量和“与”、“或”、“非”三种运算 符所构成的表达式。 由真值表可以转换为函数表达式。例如，由“三人表决”函数的真 值表可写出逻辑表达式：
L ABC ABC ABC ABC
1.3 逻辑函数的代数化简法
一、逻辑函数式的常见形式
一个逻辑函数的表达式不是唯一的，可以有多种形 式，并且能互相转换。例如：
其中，与—或表达式是逻辑函数的最基本表达形式。
二、逻辑函数的最简“与—或表 达式” 的标准
（1）与项最少，即表达式中“+”号最少。 （2）每个与项中的变量数最少，即表达式中 “· ”号最少。
3．用卡诺图化简逻辑函数的步骤：
（1）画出逻辑函数的卡诺图。 （2）合并相邻的最小项，即根据前述原则画圈。 （3）写出化简后的表达式。每一个圈写一个最简与项，规 则是，取值为l的变量用原变量表示，取值为0的变量用反变 量表示，将这些变量相与。然后将所有与项进行逻辑加，即 得最简与—或表达式
例
用卡诺图化简逻辑函数：
L( A, B, C) AB AC
解：
L( A, B, C) AB AC AB(C C) AC( B B)
ABC ABC ABC ABC

uC
(t)
uS
(t)
即
uC
(t)
1 RC
uC
(t)
1 RC
uS (t)
信号与系统 2.1-2
图1
对图1(b)，有
L R
diL (t) dt
iL
(t)
iS
(t)
即
iL (t)
R L
iL (t)
R L
iS (t)
一般形式：
y(t) ay(t) g(t)
信号与系统 2.1-3
信号与系统 2.1-4

2t
2e3t
1
瞬态响应 稳态响应
信号与系统 2.1-8
完全响应：
y(t) yzi (t) yzs (t) (ZIR) (ZSR)
响应的分类方法：
按响应的不同起因：分为储能响应和受激响应； 自由响应：取决于系统性质，即特征根； 强迫响应：取决于输入信号的形式； 瞬态响应：当t无限增长，响应最终趋于零； 稳态响应：响应恒定或为某个稳态函数。
0
例 对于书例2-1一阶系统
信号与系统 2.1-7
uC (t) 2uC (t) 2uS (t)
当uC(0)=4V， uS(t)=1+e3t 时，则完全响应为：
uC (t) 4e2t e2t 2e3t1 零输入响应 零状态响应
（储能响应）（受迫响应）
4e2te2t 12e3t 自由响应 强迫响应
➢
阅读与思考：如何理解和应用式
t
y(t) 0 g( )x1(t )d ?
end
对图2的二阶系统，则有
uC
(t)
R L
uC
(t)
1 LC
uC

. 学习参考. 第六章6.4 根据下列象函数及所标注的收敛域，求其所对应的原序列。

（1）1)(=z F ，全z 平面（2）∞<=z z z F ,)(3（3）0,)(1>=-z z z F（4）∞<<-+=-z z z z F 0,12)(2（5）a z az z F >-=-,11)(1（6）a z az z F <-=-,11)(1. 学习参考.6.5 已知1)(↔k δ，az z k a k -↔)(ε，2)1()(-↔z z k k ε，试利用z 变换的性质求下列序列的z 变换并注明收敛域。

. 学习参考 .（1）)(])1(1[21k k ε-+ （3）)()1(k k k ε-（5）)1()1(--k k k ε （7）)]4()([--k k k εε（9）)()2cos()21(k k k επ. 学习参考.6.8 若因果序列的z 变换)(z F 如下，能否应用终值定理？如果能，求出)(lim k f k ∞→。

（1）)31)(21(1)(2+-+=z z z z F （3）)2)(1()(2--=z z z z F. 学习参考.6.10 求下列象函数的双边逆z 变换。

（1）31,)31)(21(1)(2<--+=z z z z z F （2）21,)31)(21()(2>--=z z z z z F （3）21,)1()21()(23<--=z z z z z F. 学习参考 .（4）2131,)1()21()(23<<--=z z z z z F. 学习参考.. 学习参考.. 学习参考.. 学习参考.6.11 求下列象函数的逆z 变换。

（1）1,11)(2>+=z z z F （2）1,)1)(1()(22>+--+=z z z z z z z F （5）1,)1)(1()(2>--=z z z z z F （6）a z a z az z z F >-+=,)()(32. 学习参考.. 学习参考.. 学习参考.6.13 如因果序列)()(z F k f ，试求下列序列的z 变换。