Y
6
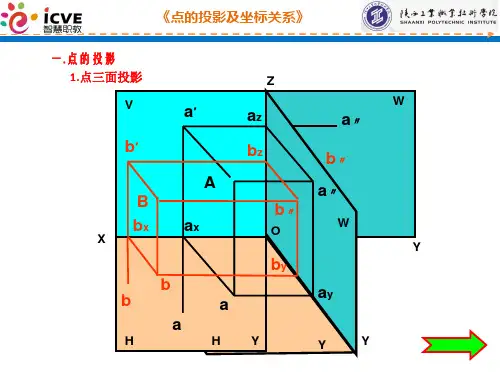
[二] 点的三面投影
z
a
a
az
x
ax o
ay
45
a
ay
投影特性:
垂直关系
aa,,aa,,
OX OZ
yW 相等关系
a ax a,,az
yH 7
三投影面体系中点的投影规律
Z
V a
az
V
a
y
x
a
X
ax
z
O W X ax
Z
W
az
a
O ay YW
a H
ay
ay
YH a
YH
1. aaz = aay = x
b
c
B
C
a
X
O
直线上的点具有两个特性:
A cb c
a
1 从属性 若点在直线上,则点的各个投影必在 直线的各同面投影上。
2 定比性 属于线段上的点分割线段之比等于其 投影之比。
例1 判断 E、F点是不是在直线AB上。
a, e,
f , b,
a e
f b
E点在AB直线上 F点不在AB直线上
10
例2 试判断K点是否在直线EF上。
a
a
X
O
YW
a YH
例题2 已知点 A的正面投影和侧面投影, 求其水平投影。
z
a
a
x
O
yW
a yH
注: 这是二求三问题的基础。
8
三 点的投影与直角坐标的关系
投影面→坐标面 投影轴→坐标轴 轴的交点O→坐标原点
距离的关系:
Aa=Xa
X
Aa =Ya
投影 坐标