时间序列分析报告-降水量预测模型
- 格式:doc
- 大小:916.00 KB
- 文档页数:9

时间序列模型在降水量预测中的应用研究随着气候变化的不断加剧,气象预测和气候变化研究变得日益重要。
其中,降水量预测是气象预测的一个关键领域,对于农业、水资源管理、城市规划等具有重要意义。
时间序列模型作为一种重要的预测方法,其在降水量预测中的应用研究备受关注。
本文旨在就时间序列模型在降水量预测中的应用研究进行探讨,从理论基础、模型选择、数据处理、结果分析等方面展开深入讨论。
一、理论基础时间序列模型是一种利用时间上的观测结果进行预测的统计模型。
其基本思想是将时间序列数据看作自回归过程或移动平均过程,利用历史数据来预测未来的趋势。
常用的时间序列模型包括自回归模型(AR)、移动平均模型(MA)、自回归移动平均模型(ARMA)、差分自回归移动平均模型(ARIMA)等。
这些模型在时间序列分析中得到了广泛应用,尤其在经济、金融等领域取得了良好的效果。
二、模型选择在降水量预测中,选择合适的时间序列模型对于预测结果的准确性至关重要。
一般来说,可以根据观测数据的特点来选择合适的模型。
如果观测数据呈现出明显的趋势和季节性变化,则可以选择ARIMA模型;如果观测数据存在自相关性和移动平均性,则可以选择ARMA模型。
除了以上基本模型外,还可以结合实际情况,采用灰色模型、神经网络模型等进行降水量预测。
在选择模型时,需要进行充分的模型比较和验证,以确保选取的模型能够较好地拟合观测数据,并且具有良好的预测性能。
三、数据处理在进行降水量预测时,需要对观测数据进行充分的处理和分析。
首先需要对观测数据进行平稳性检验,确定是否需要进行差分处理;其次需要对观测数据进行白噪声检验,以验证是否存在自相关性和移动平均性;最后需要对观测数据进行季节性调整,以消除季节性因素的影响。
在数据处理的过程中,需结合实际情况,充分利用专业知识和经验,以确保处理后的数据能够满足时间序列模型的建模要求。
四、结果分析经过以上步骤的处理和分析,得到了时间序列模型的预测结果。


雨量预报分析的评价模型数学建模雨量预报是一种重要的气象预报,用于预测未来一段时间内降水的情况。
准确的雨量预报对于农业、水利、交通等行业的决策与管理具有重要的参考价值。
评价雨量预报分析模型的有效性和精度是提高气象预报准确性的关键。
本文将介绍雨量预报分析评价模型的数学建模方法。
一、问题的提出针对雨量预报分析评价的问题,我们首先需要明确预报模型的性质,即预报模型的目标和任务。
通常来说,雨量预报的目标是通过利用历史观测数据和其他气象因素,建立一个数学模型,预测未来一段时间内的降水量。
预报模型通常采用时间序列分析、回归分析、神经网络等方法进行建模。
评价预报模型的目标是对预测结果的准确性进行评估,从而确定预报模型的好坏程度,为实际的预报工作提供科学依据。
二、评价指标的选择在评价雨量预报分析模型时,我们通常使用以下几个指标来评价其准确性:1.预报误差:预报误差是指预报结果与实际观测结果之间的差异。
常见的预报误差指标有均方根误差(RMSE)、平均绝对误差(MAE)等。
这些指标可以用来评估预报结果的整体误差水平。
2.相关系数:相关系数衡量了预报结果与实际观测结果之间的相关性。
通过评估相关系数可以确定预报模型是否具有一定的预测能力。
3.偏差分析:偏差分析主要是对预测结果的偏差进行评估。
可以通过统计偏差的分布情况和变化趋势,评估预报模型对不同时空尺度的预测能力。
三、数学模型的建立为了评价雨量预报分析模型的准确性,我们可以建立以下数学模型:1.假设预报结果为y,实际观测结果为x,预报误差为δ,则预报误差的计算可以使用均方根误差(RMSE):RMSE = sqrt(sum((y-x)^2)/n)2. 相关系数的计算可以使用皮尔逊相关系数(Pearson correlation coefficient),用来评估预报结果与实际观测结果之间的相关程度:r = sum((x-x_mean)*(y-y_mean)) / sqrt(sum((x-x_mean)^2)*sum((y-y_mean)^2))3.偏差分析可以使用直方图和箱线图等方法来进行可视化分析,评估预报模型在不同时空尺度上的偏差情况。

我国降雨分析实验报告引言降水是气象学中的重要研究内容,对于社会经济发展和生态环境具有重要影响。
了解我国降水情况并进行分析,对于气候预测、灾害防御和农业生产等方面都具有重要意义。
本实验旨在通过对我国不同地区的降雨数据进行分析,探究降水特点和分布规律。
实验方法数据获取和处理在本次实验中,我们通过公开数据源获取了我国不同地区的历史降雨数据。
经过初步筛选和清洗,我们得到了具有一定代表性的数据样本,包含了我国各省级行政区在过去30年的降水量记录。
数据处理过程中采用了以下方法:1. 去除异常数据:排除了记录时间不完整或与气象观测系统不匹配的数据;2. 数据标准化:将每个地区的降水量数据进行标准化处理,将其转化为相对值,便于跨地区对比分析。
数据分析在数据处理完成后,我们运用统计学方法和可视化工具对降水数据进行了进一步的分析。
1. 描述性统计:通过计算每个地区的平均降水量、最大降水量和最小降水量等指标,了解各地区的降水情况;2. 空间分布图:利用地理信息系统(GIS)技术,生成了我国降水分布的空间热力图,观察降水在全国范围内的分布情况;3. 趋势分析:通过建立时间序列模型,分析不同地区的降水变化趋势,判断是否存在长期变化。
实验结果描述性统计根据数据分析结果,我国平均降水量最大的省份是广东、湖南和四川,分别为1500毫米、1400毫米和1300毫米。
而平均降水量最小的省份主要集中在西部地区,如青海、新疆和西藏,平均降水量仅在200毫米以下。
最大降水量的地区主要分布在福建、台湾、广东等沿海地区和山区,这些地方由于地形和气候因素的影响,降水量较大。
相反,最小降水量的地区多为内陆地区,受到地形和气流的限制,降水量较少。
空间分布图通过生成的空间热力图,我们可以直观地观察到我国降水在全国范围内的分布情况。
从图中可以明显看出,我国东部地区的降水量普遍较大,尤其是沿海地带和山区。
而西部地区的降水量相对较小,主要集中在西北地区一带。

用动态时间序列周期分析预测模型作郑州汛期降水预报
马体顺;李社宗;赵海青;吴德义;王彦涛
【期刊名称】《气象与环境科学》
【年(卷),期】2006(000)002
【摘要】动态时间序列周期分析预测模型是将多层递阶方法与逐步回归周期分析的基本原理相结合,可以有效地选取时间序列的各个隐含周期.利用所选取的隐含周期,可作更长时间的预测.本文以郑州汛期降水为样本,对该预测模型进行了应用及讨论.
【总页数】2页(P36-37)
【作者】马体顺;李社宗;赵海青;吴德义;王彦涛
【作者单位】郑州市气象局河南郑州 450005;郑州市气象局河南郑州 450005;郑州市气象局河南郑州 450005;郑州市气象局河南郑州 450005;郑州市气象局河南郑州 450005
【正文语种】中文
【中图分类】P4
【相关文献】
1.时间序列分析方法在郑州市降水量预报中的应用 [J], 吕志涛
2.用方差分析周期及随机时间序列法作赫章6—8月总降雨量预报 [J], 吴劲松
3.逐步回归周期分析与多层递阶方法相结合的时间序列分析预报模型 [J], 李邦宪
4.时间序列周期分析法——用于中国男子跳远中期预报 [J], 金报国
5.用时间序列方法作青岛降水、气温分析和预报 [J], 李亚军;邱润之
因版权原因,仅展示原文概要,查看原文内容请购买。


基于时间序列分析的水利工程水位预测模型研究随着科技的不断发展,越来越多的水利工程利用高新技术实现更加智能化的运作。
其中,水位预测模型作为水利工程管理的一种重要方式,越来越受到重视。
时间序列分析是一种常见的用于水位预测的方法,本文将基于此方法,探讨水利工程水位预测模型的研究。
一、时间序列分析的介绍时间序列是一种由时间作为自变量的数据序列,在水利工程中,水位和降雨等指标的变化都可以视为时间序列。
时间序列分析是一种通过分析数据序列历史数据的变化规律,从而对未来进行预测的方法。
时间序列分析通常由三部分组成,分别是趋势分析、季节性分析和残差分析。
趋势分析针对水位的长期趋势变化进行预测,季节性分析针对水位的周期性变化进行预测,残差分析则是处理预测偏差的过程。
通常来说,时间序列分析的模型都比较简单明了,可以方便地应用于水利工程的实际管理中。
二、水利工程水位预测模型的研究水利工程水位预测模型是一种常见的预测模型,利用时间序列分析对历史数据进行分析,然后根据预测模型预测未来的水位变化。
水位预测模型主要分为两种,分别是单变量预测模型和多变量预测模型。
1. 单变量预测模型单变量预测模型通常只考虑水位自身的变化,常见的模型包括移动平均模型、指数平滑模型和自回归模型等。
其中,自回归模型通常用AR表示,AR(p)模型是指当期水位与前p期水位直接相关。
移动平均模型通过平均历史数据来预测未来的水位变化。
指数平滑模型则是通过加权历史数据来实现预测,一些常见的指数平滑模型包括简单指数平滑模型、霍尔特指数平滑模型和关键点指数平滑模型等。
2. 多变量预测模型多变量预测模型考虑了多个因素对水位变化的影响。
这些因素可以是降雨量、温度等自然因素,也可以是水位调控等人为因素。
多变量预测模型通常利用回归分析、灰色系统理论等方法,建立多因素与水位变化之间的关系模型。
三、水利工程水位预测模型的应用水利工程水位预测模型广泛应用于水电站、堤防、灌溉系统等领域。
![[论文]时间序列分析-降水量预测模型](https://uimg.taocdn.com/b3287ae4aef8941ea76e054e.webp)
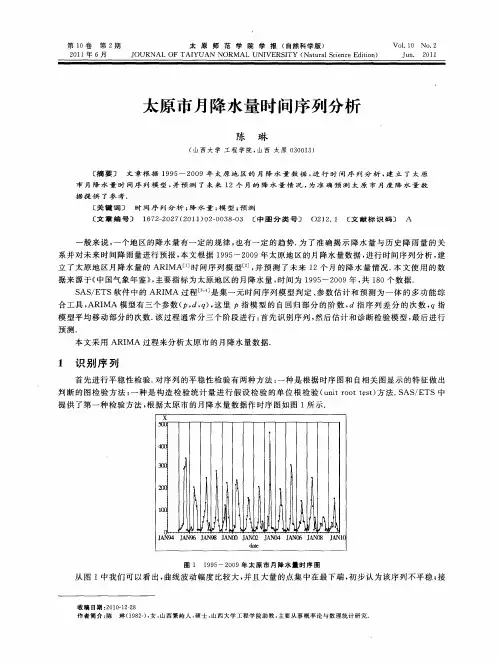
实验报告课程名称:时间序列分析设计题目:降水量预测模型院系:电子信息与工程学院班级:电子二班设计者:学号:指导教师:设计时间:2010/05/071. 实验选题课程设计以国家黄河水利委员会建站的山西省河曲水文站1952年至2002年51年的资料为例,以1952年至2001年50年的降水序列作为样本,建立线性时间序列模型并预测2002年的降水状态与降水量,并与2002年的实际数据比较说明本模型的具体应用及预测效果。
资料数据见表1。
表1 山西省河曲水文站55年降水量时间序列时段降水量(mm) 时段降水量(mm) 时段降水量(mm)1952 1953 1954 1955 1956 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966 1967 1968 1969 1970 261.6486.4631.5259.0568.0398.2479.6697.6397.7640.4247.1387.7694.2211.4322.6656.6325.3603.8424.81971197219731974197519761977197819791980198119821983198419851986198719881989383.3238.8423.0237.1330.7445.9518.9492.6490.3257.0400.6347.5368.3411.5356.2381.2318.0473.0373.31990199119921993199419951996199719981999200020012002369.0348.3469.2228.1338.8546.1358.9237.1423.3257.4234.4389.6487.3- 1 -- 2 -2.实验原理2.1模型表示均值为0,具有有理谱密度的平稳时间序列的线性随机模型的三种形式,描述如下: 1、()AR p 自回归模型:1122t t t p t p t ωφωφωφωα-------=由2p +个参数刻画;2、()MA q 滑动平均模型:1122t t t t q t q ωαθαθαθα---=----由2q +个参数刻画;3、(,)ARMA p q 混和模型:11221122t t t p t p t t t q t q ωφωφωφωαθαθαθα----------=----(,)ARMA p q 混和模型由3p q ++个参数刻画;2.2 自相关函数k ρ和偏相关函数kk φ1、自相关函数k ρ刻画了任意两个时刻之间的关系,0/k k ργγ=2、偏相关函数kk φ刻画了平稳序列任意一个长1k +的片段在中间值11,t t k ωω++-固定的条件下,两端t ω,t k ω+的线性联系密切程度。

基于时间序列分析的降雨预测研究近年来,气候变化导致的极端天气现象频繁出现,降雨量的不稳定性越来越大。
对于农业、城市建设等领域来说,如何准确预测降雨量的变化越来越重要。
其中,基于时间序列分析的降雨预测研究备受关注。
时间序列分析是指对某种现象在时间上变化的特点进行分析、处理,通常是对时间序列中的特征和规律进行探究。
在气象学领域,时间序列分析被广泛应用于气象要素的预测与决策。
目前,气象事业的发展和数据采集技术的提高,使得时间序列分析在降雨预测方面展现出了广泛的应用前景。
一般来说,时间序列分析的预测方法主要分为线性和非线性两种。
其中,线性方法主要包括平稳时间序列、自回归移动平均模型(ARMA)和自回归综合移动平均模型(ARIMA)等,而非线性方法包括人工神经网络(ANN)和支持向量机(SVM)等。
在实际应用中,不同的预测方法选择会受到降雨数据采样精度、数据的周期性特征以及预测目标要求等因素的影响。
具体而言,平稳时间序列是时间序列预测中较为简单的方法,最为传统的应用方法是移动平均法。
而ARMA和ARIMA模型则能够较准确地预测出降雨量的变化趋势和周期。
据研究显示,ARIMA模型在预测降雨时具有较好的预测效果,可对周或月的降雨量进行短期预测。
对于长期预测则需要考虑到时间序列的季节性特征,目前已出现了以ARIMA为基础的季节自回归综合移动平均模型(SARIMA)。
除此之外,非线性预测方法也被广泛应用于降雨量的预测中。
人工神经网络预测模型能够对时间序列中的非线性特征进行更好的处理,通过选择不同的网络结构和算法,可提高预测效果。
而支持向量机方法则可以将时间序列预测转化为优化问题,并通过寻找最优决策平面来实现预测目标。
综上所述,基于时间序列分析的降雨预测研究对于解决极端天气带来的影响具有重要意义。
不同的预测方法选择应根据实际情况以及数据特征等因素综合考虑。
当然,在实践中,还需要不断完善预测模型,提高数据采样精度以及数据预处理方法,来实现更为准确的降雨预测。

课程名称: 时间序列分析题目: 降水量预测院系:理学院专业班级:数学与应用数学10-1 学号: 87学生姓名:戴永红指导教师:__潘洁_2013年 12 月 13日1.问题提出能不能通过以前的降水序列为样本预测出2002的降水量?2.选题以国家黄河水利委员会建站的山西省河曲水文站1952年至2002年51年的资料为例,以1952年至2001年50年的降水序列作为样本,建立线性时间序列模型并预测2002年的降水状态与降水量,并与2002年的实际数据比较说明本模型的具体应用及预测效果。
资料数据见表1。
表1 山西省河曲水文站55年降水量时间序列3.原理 模型表示均值为0,具有有理谱密度的平稳时间序列的线性随机模型的三种形式,描述如下:1、()AR p 自回归模型:1122t t t p t p t ωφωφωφωα-------=L 由2p +个参数刻画;2、()MA q 滑动平均模型:1122t t t t q t q ωαθαθαθα---=----L 由2q +个参数刻画;3、(,)ARMA p q 混和模型:11221122t t t p t p t t t q t q ωφωφωφωαθαθαθα----------=----L L(,)ARMA p q 混和模型由3p q ++个参数刻画; 自相关函数k ρ和偏相关函数kk φ1、自相关函数k ρ刻画了任意两个时刻之间的关系,0/k k ργγ=2、偏相关函数kk φ刻画了平稳序列任意一个长1k +的片段在中间值11,t t k ωω++-L 固定的条件下,两端t ω,t k ω+的线性联系密切程度。
3、线性模型k ρ、kk φ的性质表2 三种线性模型下相关函数性质模型识别通常平稳时间序列t Z ,0,1t =±L 仅进行有限n 次测量(50)n ≥,得到一个样本函数,且利用平稳序列各态历经性:11nj j Z Z n μ=≈=∑做变换,t t Z ω=,1,t n =L ,将1,,n Z Z L 样本换算成为样本1,,n ωωL ,然后再确定平稳时间序列{,0,1}t t ω=±L 的随机线性模型。
基于时间序列模型的降雨量预测分析程敏;张耀文;姜纪沂;任杰;赵振宏【摘要】为了解济南市未来降雨的变化情况,以济南市1959~2015年降雨量数据为研究对象运用SPSS软件中时间序列模型ARIMA对其进行了建模;拟合1959~2015年的降雨量数据及预测未来5年的降雨量.ARIMA模型预测结果表明了济南市2016~2020年的年降雨量依次为676.5,635.5,689.8,630.7,663.3mm,5年的年平均降雨量为659.2mm,这与过去57年的多年平均降雨量较为接近,可以依此推测济南市未来5年出现干旱及洪涝灾害的可能性较小.可以看出,影响ARIMA模型预测结果的因素有很多,为了更加精准地预测降雨量,应当考虑多种要素并结合当地具体环境,建立符合当地的降水量预测模型.【期刊名称】《水科学与工程技术》【年(卷),期】2019(000)001【总页数】5页(P1-5)【关键词】时间序列模型;ARIMA模型;预测;降雨量;SPSS【作者】程敏;张耀文;姜纪沂;任杰;赵振宏【作者单位】防灾科技学院,北京101601;防灾科技学院,北京101601;防灾科技学院,北京101601;防灾科技学院,北京101601;中国地质调查局西安地质调查中心,西安710054【正文语种】中文【中图分类】TV122降雨量的短期变化,往往会造成严重的干旱涝、洪灾害,并对当地经济发展等造成不同程度的影响。
高精度的降雨量预测方法能及早地发现降雨量变化情况,提高应对此类灾害的能力[1]。
降雨量是衡量干旱程度的一个重要指标,直接反映了自然界的变化,降雨量的大小直接影响农业生产[2]。
如能对降雨量做出科学准确预测,农业、水利等有关部门就可以及时采取防涝抗旱措施[3],降低不必要的损失,因此降雨量预测已成为当前预测中的重要研究课题[4]。
对于水资源短缺的北方来说,地下水是北方的主要用水来源,高精度的预测降雨量,能最大限度的利用水资源,将多余的水储存起来,以缓解水资源短缺问题,降低因水资源短缺或极度缺少而带来的经济损失。
月降雨量系列的时间序列模型分析的探讨陈家寿(福建省沙县城关水电有限公司,福建沙县城关365500)摘要:本文简要概述了时间序列概念、序列的平稳性分析和转化、序列分析模型种类、AR、MA、ARMA模型识别和参数估计方法,并根据沙县水文站1988年至2007年的逐月降雨系列资料,对其进行时间序列平稳性分析、序列模型分析及短期预测应用。
关健词:月降雨量时间序列分析自然现象受自然界各种因素如气候、环境以及人为活动影响,其变化规律极其复杂,如水文现象中的雨量,对其用物理的方法加以分析,往往因其影响因素未全面了解而导致分析模型的复杂和效果不理想。
在实际中,常用统计模型来模拟,本文即讨论了用时间序列方法对福建省沙县水文站月降雨量序列加以分析。
1. 时间序列方法简介时间序列概念某个随另一变量(往往取时间t)变化而变化的量X(t),在t1<t2<…<t n<…处的实测值组成的离散有序集合,称为一个时间序列,记作{ X(t)}。
客观中多数情况可认为时间序列由某个随机过程产生,可描述为由反映趋势变化的趋势项f(t)、反映周期变化的周期项p(t)和随机项a(t)三部分组成,根据趋势项、周期项的不同情况,可将序列分为平稳的和非平稳的:当f(t)及p(t)为常数时,则称其取样值Xi(x1,x2,…x n)为平稳时间序列;当f(t)及p(t)不全为常数时,则称其取样值Xi为非平稳时间序列。
对时间序列分析,往往将非平稳时间序列化为平稳序列,因其模型识别效果较好。
对非平稳时间序列,可通过对Xi作一阶或p阶差分变化,将其化为平稳序列,如作一阶差分变化为:▽x(t)=x t-x t-1 (t=2, ...,n) (1)对于有周期性变化趋势的,也可作季节性差分变化,如序列x(t) 的周期d=12 则:▽z t =x t-x t-12(t=13,14, ...,n) (2)也可对原序列兼作上述两种变化,如对原序列x(t)先作季节性差分变化再作一阶差分变化,如下:▽(▽z t)= ▽z t-▽z t-1 (t=2, ...,n) (3)经过上述变化,往往可将原序列化为平稳序列。
对镇江市近几年降雨量数据进行时间序列分析及预测一、引言最早的时间序列分析可以追溯到7000年前的古埃及。
当时,为了发展农业生产,古埃及人一直在密切关注尼罗河泛滥的规律。
把尼罗河涨落的情况逐天记录下来,就构成了所谓的时间序列。
对这个时间序列长期的观察使他们发现尼罗河的涨落非常有规律。
天狼星第一次和太阳同时升起的那一天之后,再过200天左右,尼罗河就开始泛滥,泛滥期将持续七八十天,洪水过后,土地肥沃,随意播种就会有丰厚的收成。
由于掌握了尼罗河泛滥的规律,古埃及的农业迅速发展,解放出大批的劳动力去从事非农业生产,从而创建了古埃及灿烂的史前文明。
像古埃及人一样,按照时间的顺序把随机事件变化发展的过程记录下来就构成了一个时间序列。
对时间序列进行观察、研究,找寻它变化发展的规律,预测它将来的走势就是时间序列分析。
由此可见,时间序列分析在我们生活中将扮演着一个十分重要的角色。
于是,我们先进行时间序列的定义。
在统计研究中,常用按时间顺序排列的一组随机变量……,X1,X2,……,Xt,……来表示一个随机事件的时间序列,简记为{Xt,t∈T}或{Xt}用x1,x2,……,xn或{xt,t=1,2,…,n}表示该随机序列的n个有序观察值,称之为序列长度为n的观察值序列。
二、文献综述及数据来源为充分了解时间序列在生活中的应用,本例就取镇江市近几年的降雨量数据进行时间序列分析,并在进行模型建设及检验完毕后,对2010年的月降雨量进行预测,并进行真实值的校对,以确认时间序列在生活中的有效应用。
本例数据来源于江苏省统计年鉴2000—2009年,其中参考文献为中国人民大学出版社出版的《应用时间序列分析》。
关键字:时间序列模型建设检验预测三、数据展示及描述性分析数据来源于江苏省统计年鉴2000—2009,选取的是镇江市从2000年到2009年的月降雨量。
由描述统计量表得出,镇江市近几年的月降雨量在90.7925间波动,且极小值与极大值之间的差距还是挺大的,说明降雨量是一个具有季节性的数据。
课程名称: 时间序列分析题目: 降水量预测院系:理学院专业班级:数学与应用数学10-1学号:学生姓名:戴永红指导教师:__潘洁_2013年 12 月 13日1.问题提出能不能通过以前的降水序列为样本预测出2002的降水量?2.选题以国家黄河水利委员会建站的山西省河曲水文站1952年至2002年51年的资料为例,以1952年至2001年50年的降水序列作为样本,建立线性时间序列模型并预测2002年的降水状态与降水量,并与2002年的实际数据比较说明本模型的具体应用及预测效果。
资料数据见表1。
表1 山西省河曲水文站55年降水量时间序列3.原理 3.1模型表示均值为0,具有有理谱密度的平稳时间序列的线性随机模型的三种形式,描述如下:1、()AR p 自回归模型:1122t t t p t p t ωφωφωφωα-------=由2p +个参数刻画;2、()MA q 滑动平均模型:1122t t t t q t q ωαθαθαθα---=----由2q +个参数刻画;3、(,)ARMA p q 混和模型:(,)ARMA p q 混和模型由3p q ++个参数刻画; 3.2 自相关函数k ρ和偏相关函数kk φ1、自相关函数k ρ刻画了任意两个时刻之间的关系,0/k k ργγ=2、偏相关函数kk φ刻画了平稳序列任意一个长1k +的片段在中间值11,t t k ωω++-固定的条件下,两端t ω,t k ω+的线性联系密切程度。
3、线性模型k ρ、kk φ的性质表2 三种线性模型下相关函数性质3.3 模型识别通常平稳时间序列t Z ,0,1t =±仅进行有限n 次测量(50)n ≥,得到一个样本函数,且利用平稳序列各态历经性:11nj j Z Z n μ=≈=∑做变换,t t Z ω=,1,t n =,将1,,n Z Z 样本换算成为样本1,,n ωω,然后再确定平稳时间序列{,0,1}t t ω=±的随机线性模型。
课程名称: 时间序列分析题目: 降水量预测院系:理学院专业班级:数学与应用数学10-1学号: 87学生姓名:戴永红指导教师:__潘洁_2013年 12 月 13日1.问题提出能不能通过以前的降水序列为样本预测出2002的降水量2.选题以国家黄河水利委员会建站的山西省河曲水文站1952年至2002年51年的资料为例,以1952年至2001年50年的降水序列作为样本,建立线性时间序列模型并预测2002年的降水状态与降水量,并与2002年的实际数据比较说明本模型的具体应用及预测效果。
资料数据见表1。
表1 山西省河曲水文站55年降水量时间序列3.原理模型表示均值为0,具有有理谱密度的平稳时间序列的线性随机模型的三种形式,描述如下:1、()AR p 自回归模型:1122t t t p t p t ωφωφωφωα-------=由2p +个参数刻画;2、()MA q 滑动平均模型:1122t t t t q t q ωαθαθαθα---=----由2q +个参数刻画;3、(,)ARMA p q 混和模型:11221122t t t p t p t t t q t q ωφωφωφωαθαθαθα----------=----(,)ARMA p q 混和模型由3p q ++个参数刻画; 自相关函数k ρ和偏相关函数kk φ1、自相关函数k ρ刻画了任意两个时刻之间的关系,0/k k ργγ=2、偏相关函数kk φ刻画了平稳序列任意一个长1k +的片段在中间值11,t t k ωω++-固定的条件下,两端t ω,t k ω+的线性联系密切程度。
3、线性模型k ρ、kk φ的性质表2 三种线性模型下相关函数性质模型识别通常平稳时间序列t Z ,0,1t =±仅进行有限n 次测量(50)n ≥,得到一个样本函数,且利用平稳序列各态历经性:11nj j Z Z n μ=≈=∑做变换,t t Z ω=,1,t n =,将1,,n Z Z 样本换算成为样本1,,n ωω,然后再确定平稳时间序列{,0,1}t t ω=±的随机线性模型。
样本自相关函数平稳序列21012,,,,,ωωωωω--, ()0t E ω=,对于样本,定义自协方差函数:112211ˆn kk k n k nk j k j j nn ωωωωωωγωω-++-+=+++==∑,0ˆˆˆ/k k ργγ=。
同时为了保证ˆk k γγ=,ˆk k ρρ=一般取50,/4n k n ><。
常取/10k n =。
确定模型类别和阶数在实际应用中,我们常用有一个样本算出的ˆk k ρρ=,ˆkk kkφφ=判别k ρ,kk φ是拖尾还是截尾的。
随机线性模型的三种形式的判别分别如下:1、若k ρ拖尾,kk φ截尾在k p =处,则线性模型为()AR p 模型。
kρ拖尾可以用的点图判断,只要样本自相关函数的绝对值愈变愈小;当k p >时,平均20个样本偏相关函数中至多有一个使ˆ2kkφ≥,则认为kk φ截尾在k p =处。
2、若kk φ截尾,kρ在k p =处截尾,那么线性模型为()MA q 滑动平均模型。
kk φ拖尾可以根据样本偏相关函数的点图判断,只要ˆkk φ愈变愈小。
当k q >时,若平均20个样本自相关函数中至多有一个使ˆ2k ρ≥ 3、若样本自相关函数和样本偏相关函数都是拖尾的,则线性模型可以看成混和模型。
模型参数估计1、()AR p 模型参数估计:()AR p 模型有2p +个参数:212,,,,,p p αφφφσ。
利用Yule-Walker 方程,利用Toeplitz 矩阵求逆和作矩阵乘法的方法算样本偏相关函数kk φ。
()AR p 模型的参数值不必作专门的计算,只要在样本偏相关函数计算的记录中取出样本参数值即可。
此时12,,,p φφφ,都已经确定了,经过推理我们可以得到:201pj j j ασγφγ==-∑。
2、()MA q 滑动平均模型参数估计:22221221+1ˆˆˆˆ(1),0ˆˆˆˆˆˆˆ(),1qk k k q k q k k q αασθθθγσθθθθθ-⎧++++=⎪=⎨-+++≤≤⎪⎩ 可得1q +个方程,求212ˆˆˆˆ,,qαθθθσ,即解这个非线性方程组。
3、(,)ARMA p q 混和模型参数估计对于满足一个条件:1111......t t p t p t t p t q a a a ωφωφωθθ-------=---采用先计算 12ˆˆˆ,,,p φφφ,在计算212ˆˆˆˆ,,qαθθθσ的方法,具体如下:1)可利用Toeplitz 矩阵和作矩阵乘法的方法求出12ˆˆˆ,,,pφφφ。
2)令'11...t t t p t p ωωφωφω--=---混和模型化为:'11...t t t p t q a a a ωθθ--==---这是关于't ω的()MA q 模型,用't ω的样本协方差函数估计212ˆˆˆˆ,,q αθθθσ的值。
4. 步骤采用MATLAB 处理数据。
1、对一个时间序列做n 次测量得到一个样本函数12,,n Z Z Z 。
实验采用表1中的降水量数据,50n =。
图1 山西省河曲水文站55年降水量时间序列2、数据预先处理:做变换t tZ Zω=-,其中501150jjZ Z==∑图2 将时间序列变为期望为0的平稳时间序列3、计算样本自协方差函数kγ,样本自方差函数kρ。
ˆˆˆ/k kργγ=,其中0,1,2,3,4,5k=,112211ˆn kk k n k nk j k jjn nωωωωωωγωω-++-+=+++==∑。
由图-3数据可得:随着k的增大,kρ越来越小,具有拖尾性。
图3 计算样本自相关函数接下来计算偏相关函数kkφ(1k≥)。
利用Yule-Walker方程,利用Toeplitz矩阵求逆和作矩阵乘法的方法算样本偏相关函数kkφ。
2/500.283=,由图-4得到的数据可得,2k p>=时,只有一个偏相关函数大于。
所以确定阶数为:2p=。
图4计算偏相关函数5、由上综述:确定模型为(2)AR模型。
下面进行(2)AR模型参数的估计。
111ˆˆ0.1695φφ==-,222ˆˆ0.0190φφ==-,由图-3的,0ˆ 1.6320e+004γ=,由公式21pj jjασγφγ==-∑得:2ˆ 1.5855e+004ασ=图5 噪声方差的计算由上可知模型为:120.16950.0190t t t tωωωα--++=,又知11402.82nj j Z Z n ===∑,12402.820.1695(402.82)0.0190(402.82)t t t t Z Z Z α---+-+-=,2ˆ 1.5855e+004ασ=。
最后确定(2)AR 模型为:120.16950.0190478.75t t t t Z Z Z α--++=+,2ˆ 1.5855e+004ασ= 6、通过确定的模型估计2002年的降水量一步估计公式:1ˆˆˆ(1)(1)0.16950.0190478.75k k k Z Z k Z Z -=+=--+。
其中,2001年的降水量为,2001年的降水量为。
20020.1695*234.40.0190*389.6478.75431.62Z =--+=mm一步预报误差为79.66=mm ,而2002年实际降水量为。
为了提高预报准确度,可以提供更多样本点,进行预报估计。
5.部分程序代码及注释rainfall=[ ……];b=length(rainfall);z=sum(rainfall)/b; ………………………………计算均值 w=rainfall-z; ………………………………由t Z 构造t ω序列 sumw=zeros(1,6); sumw1=0; for j=1:50sumw1=sumw1+w(j)^2; ..……………………………..计算0γ endfor k=0:5 for i=1:(b-k)sumw(k+1)=sumw(k+1)+w(i)*w(i+k); …………….......计算k γ end endr=sumw/b; r0=sumw1/b;p=r/r0; ……………………….计算自相关函数k ρ kk11=p(2); ………………………计算11φ a2=[1,p(2);p(2),1] a22=inv(a2);kk2=a22*p(1,2:3)'; ………………………计算22φ kk22=kk2(2,1);a5=[1,p(2),p(3),p(4),p(5);p(2),1,p(2),p(3),p(4);p(3),p(2),1,p(2),p(3);p(4),p(3),p(2) ,1,p(2);p(5),p(4),p(3),p(2),1];a55=inv(a5);kk5=a55*p(1,2:6)';φkk55=kk5(5,1); ………………..计算55kk=zeros(1,5);kk=[kk11,kk22,kk33,kk44,kk55];σD=r0-kk11*r(2)-kk22*r(3) ………………..计算2α。