下载文档原格式
博弈论及其应用——博弈论及生活中的应用（一）博弈论博弈论是专门研究两个或两个以上利益有冲突的个体，在相互作用下如何进行各自优化决策的理论。
有时也称为对策论，或者赛距理论。
是研究具有斗争或竞争性质现象的理论和方法，它是应用数学的一个分支，既是现代数学的一个新分支。
目前在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。
博弈论主要研究公式化了的激励结构间的相互作用。
是研究具有斗争或竞争性质现象的数学理论和方法。
也是运筹学的一个重要学科。
博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。
生物学家使用博弈理论来理解和预测进化论的某些结果。
博弈这一词语最早来源于棋弈。
精明慎重的棋手们相互揣摩、相互牵制，人人争赢，下出诸多精彩纷呈、变化多端的棋局。
博弈论是研究棋手们“出棋”着数中理性化、逻辑化的部分，并将其系统化为一门科学。
生活中每个人如同棋手，其每一个行为如同在一张看不见的棋盘上布一个子，精明慎重的棋手们相互揣摩、相互牵制，人人争赢，而此时博弈论也扩展到了研究个体如何在错综复杂的相互影响中得出最合理的策略。
博弈论的历史：.萌芽时期：世纪甚至更早，瓦德格拉夫()在年提出两人博弈的极小化极大混合策略解;库诺特()在年、伯特兰德()在年分别提出了博弈论中经典的经济学模型;公元前,我国的齐威王田忌赛马的博弈思想，年前巴比伦犹太教法典中的“婚姻合同问题”。
.早期研究：源于上世纪初年齐默罗()提出了关于象棋博弈的定理是博弈论的第一个定理,提出的“逆推归纳法”( )则是博弈论的第一种有着一般意义的分析方法;冯.诺伊曼( )和摩根斯坦()在年给出了扩展形博弈定义,证明了有限策略的两人零和博弈有确定的结果等.博弈论的形成：冯.诺伊曼( )和摩根斯坦()年出版了《博弈论和经济行为》( ),在该著作中,引进了博弈论的扩展形( )和正规形( )或称策略形()、矩阵形( ), 定义了极小化极大解( ),并说明了解在所有两人零和博弈中的存在性,且提出了创建博弈论的一般理论的想法,给出了博弈论的一般框架、概念术语和表示方法.《博弈论和经济行为》的出版被公认为博弈论初步形成的标志。
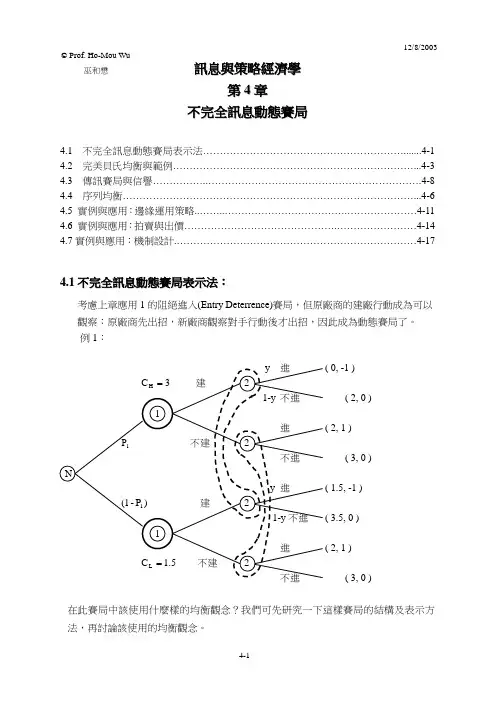
訊息與策略經濟學第4章不完全訊息動態賽局4.1 不完全訊息動態賽局表示法…………………………………………………….......4-1 4.2 完美貝氏均衡與範例………………………………………………………………...4-3 4.3 傳訊賽局與信譽……………..……………………………………………………….4-8 4.4 序列均衡……………………………………………………………………………...4-6 4.5 實例與應用：邊緣運用策略..……..……………………………….…………………4-11 4.6 實例與應用：拍賣與出價……………………………………….……………………4-14 4.7實例與應用：機制設計.………………………………………………………………4-174.1不完全訊息動態賽局表示法：考慮上章應用1的阻絕進入(Entry Deterrence)賽局，但原廠商的建廠行動成為可以觀察：原廠商先出招，新廠商觀察對手行動後才出招，因此成為動態賽局了。
例1：y 進 ( 0, -1 ) 3C H = 建 21-y 不進( 2, 0 )1進 ( 2, 1 ) 1P 不建 2不進( 3, 0 )Ny 進 ( 1.5, -1 ))P -(11 建 21-y 不進 ( 3.5, 0 ) 1進( 2, 1 )5.1C L = 不建2不進( 3, 0 )在此賽局中該使用什麼樣的均衡觀念？我們可先研究一下這樣賽局的結構及表示方法，再討論該使用的均衡觀念。
12/8/2003© Prof. Ho-Mou Wu巫和懋2’s strategy ：不因先驗機率 (prior probability) p 1改變了 觀察到原廠商已建廠x ＝1，2應選擇y ＝0（不進），嚇阻進入策略有效。
觀察到原廠商未建廠x ＝0，2應選擇y ＝1（進）1’s strategy ：3C H =高成本時：建得2，不建也得2 5.1C L =低成本時：建得3.5，不建得2因此，H x []1 ,0∈，1x L =注意在這個賽局中，1的行動也傳遞了其成本高低的訊號：原廠商低成本時一定會建廠，但觀察到1的建廠行動尚不足確認1必定為低成本(因]1,0[∈H x )，但是可能性很大(可能要用到事後機率的貝氏算法，後面再討論)。
博弈论PPT资料整理第一章博弈是一场至繁至简的游戏1928年冯诺伊曼系统证明了博弈论的基本原理，并宣告了博弈论的诞生。
1994年，纳什，海萨尼和泽尔腾曾因开创了非合作博弈均衡的分析理论活动诺贝尔经济学奖。
2005年，谢林和奥曼因把博弈论引入国家管理，获得诺贝尔经济学奖。
博弈论也称对策论，原来是数学的一个分支，但由于它比较好的解决了对竞争等问题的可操作性分析，从而发展成为经济学中的一个研究领域，并以其鲜明的特征改变了经济学的传统研究其实，博弈论就是一种关于决策和对策的博弈的理论，更多的用于人与人之间，但是，因为人的思维是随环境、心情等不断变化的。
于是对于每个人每个时间应对的策略都是变化，这就增加了博弈分析的深度和难度。
中国古代的《孙子兵法》就不仅是一部军事著作，也算是世界上最早的一部博弈论专著。
博弈是个人、团队或其他组织、面对一定的环境条件，在一定的约束条件下依靠自身掌握的信息，同时或先后、一次或多次从各自可能的行为或策略集合中做出自己的选择并予以实施，从中取得相应的结果或收益的过程。
生活中的博弈：购物商场的选择、邀请朋友聚会、财物损失的报案、城管和小贩的游击战、老师考勤和学生翘课、恋人相处的艺术人们时时刻刻都在分析并预测他人的行为并作出相应的行动选择。
而博弈也恰恰就是通过理性思维来对你在人际交往中的现象进行分析和总结，并帮助你完成优化效果的过程。
特别是在现代，可以说人们在日常生活中的一切行为均可以通过博弈论来解释，因为博弈的本质就是在进行一场生存的游戏。
由此可见，博弈论是适合所有人的科学。
在人际交往的过程中，博弈就是运用你的智慧和理性思维，在纷繁的事件中选择能够使你的利益最大达到最大化的科学。
博弈论能够起到重要的作用，由此，你可以看到博弈论在生活当中的广泛应用。
可以说作为一门关系学，它是人与人之间的行动互相影响的科学，是伴随你一生的科学。
从围棋定式谈纳什均衡过分的骗着与本手、缓手之间一般以本手应对着招过分不遇反击，则可能占到便宜，如遇反击则可能亏损如果势均力敌，则应考虑到对手的反击手段。
第四章动态不完全信息博弈第一节. 序贯均衡的内涵一.问题的提出1.序贯理性2.一致信念二.序贯均衡的内涵1.例子2.定义a.行为战略b.序贯理性c.一致信念3.存在性三.序贯均衡的计算1.例子：一般计算2.例子：分析应用第二节. 序贯均衡的应用一.教育和信号传递1.假设2.分析二.垄断限价模型1.假设2.分析三.声誉模型1.假设2.分析四.序贯均衡之再精炼1.剔除劣弱战略2.直观标准3.垄断限价模型第四章不完全信息动态博弈第一节.序贯均衡的内涵一.问题的提出1.序贯理性——参与人在所有情况决策都是理性的，即在给定信念的条件下，以及其他参与人的选择条件下，自身选择是最优的例1：子博弈最优——纳什均衡(,)L l是否合理？——如果参与人2有机会选择，肯定选r而不是l；——(,)L l不是子博弈精炼纳什均衡。
例2：单点信息集最优——纳什均衡(,,)D a l是子博弈纳什均衡；——但如果参与人2有机会选择，但肯定选择d；——(,,)D a l不满足单点信息集理性。
例3：多点信息集最优——纳什均衡(,)A r是子博弈精炼纳什均衡；——(,)A r不满足多点信息集理性。
2.一致信念例1：与客观事实一致u=是否合理？——参与人2的信念2/3——2/3u=是不合理的，因为任何到达参与人2信息集都不可能产生此后验概率；——后验信念必须与先念信念保持一致。
例2：前后信念一致——参与人2的第2个信息集上的信念，是否合理？——不合理，给定参与人战略和第1个信息集的信念，利用贝叶斯法则计算信念与此不一致；——参与人前后信念保持一致。
例3：独立偏离——参与人3的信念0.9u =是否合理？——参与人1和参与人3的偏离是独立的，所以参与人3的合理信念为0.1u =；——不同参与人之间的偏离是独立的总结，一致信念要求：参与人偏离最小化,，参与人之间偏离是独立的；二.序贯均衡的定义1.例子——定义参与人1在信息集1.1和1.3以及参与人2在2.2上的序贯理性；——定义信息集1.3和2.2的信念？2.定义a.行为战略：参与人在某个信息集到行动集映射，——如果某个状态真正发生，参与人如何决策；——序贯理性是否满足？b.序贯理性：在任何信息集上，参与人在给定信念和所有后续行为战略，选择自身行为战略最大化预期效用。
