电磁铁参数计算方式

电磁铁磁力的计算公式电磁铁的磁力计算公式：
一、电磁铁的平均磁力：
1、总质量M的电磁铁磁力（H）计算公式：
2、电磁铁的平均磁力（Hm）计算公式：
二、电磁铁的最大磁力：
1、电磁铁的最大磁力（Hmax）计算公式：
2、电磁铁的最大磁力系数 Kmax计算公式：
三、电磁铁的最小磁力：
1、电磁铁的最小磁力（Hmin）计算公式：
2、电磁铁的最小磁力系数 Kmin计算公式：
四、电磁铁U型磁力（U）计算公式：
五、电磁铁的最大磁矩（Mmax）计算公式：
1、电磁铁的最大磁矩（Mmax）计算公式：
2、电磁铁的最大磁矩系数 Kmax计算公式：
六、电磁铁的最小磁矩（Mmin）计算公式：
1、电磁铁的最小磁矩（Mmin）计算公式：
2、电磁铁的最小磁矩系数 Kmin计算公式：
七、电磁铁的轴向磁感计算公式：
1、电磁铁的轴向磁感（Gax）计算公式：
2、电磁铁的轴向磁感系数 Kax计算公式：
八、电磁铁的轴向磁矩计算公式：
1、电磁铁的轴向磁矩（Max）计算公式：
2、电磁铁的轴向磁矩系数 Kax计算公式：
九、电磁铁的轴向孔径计算公式：
1、电磁铁的轴向孔径（dax）计算公式：
2、电磁铁的轴向孔径系数 Kdax计算公式：
总结：电磁铁的磁力计算公式由以上九种，均可通过能量密度与核磁比等参数，计算出电磁铁的平均磁力、最大磁力、最小磁力、最大磁矩、最小磁矩、轴向磁感、轴向磁矩、轴向孔径等。

公式的详细计算公式需参考相关的电磁学文献进行查看。

磁芯饱和电流计算公式磁芯饱和电流是指在给定的电磁铁结构中，磁芯达到饱和状态所需的电流值。

在磁芯饱和之前，外加的电流会使磁场强度线性增加，但当磁芯饱和后，进一步增加电流将不会使磁场强度继续增加。

磁芯饱和电流是设计电磁器件时的重要参数之一，可以用来确定电磁铁的承受能力或者反推出电磁铁的尺寸和材料。

1.长圆柱形磁芯对于长圆柱形磁芯，可以使用下述公式计算饱和电流:Is=(Bd*Hc)/(4*π*L)其中，Is表示磁芯饱和电流的密度，Bd表示磁芯的饱和磁感应强度，Hc表示磁芯材料的临界磁场强度，L表示磁芯长度。

2.长方形磁芯对于长方形磁芯，可以使用下述公式计算饱和电流:Is=(2*B*H)/(L+0.8*W)其中，Is表示磁芯饱和电流，B表示磁感应强度，H表示磁场强度，L和W表示磁芯的长度和宽度。

3.E形磁芯对于E形磁芯，可以使用下述公式计算饱和电流:Is = (Bd * D * (lh + lg)) / (2 * L)其中，Is表示磁芯饱和电流，Bd表示磁芯的饱和磁感应强度，D表示磁芯的有效截面面积，lh表示磁芯中心腿的长度，lg表示磁芯两侧腿的长度，L表示磁芯的长度。

需要注意的是，这些公式仅适用于简化了非线性磁滞和温度变化的情况。

在实际应用中，磁芯饱和电流的计算通常需要结合具体的磁芯材料和工作温度条件来进行。

此外，有一些通用的方法可以用于近似地估计磁芯饱和电流。

例如，可以通过在磁芯上施加不同的电流，从而测量磁感应强度-磁场强度曲线，并从中找出磁芯饱和电流所对应的点。

此外，也可以使用有限元分析方法来模拟磁芯的磁场分布，从而得出磁芯的饱和电流。

总之，磁芯饱和电流是设计电磁器件时一个重要的参数。

使用适当的计算公式和方法，可以帮助工程师们准确地预测磁芯的饱和电流，从而设计出性能更好的电磁器件。

电磁铁的磁场强度计算电磁铁的磁场强度是其重要特性之一，对于理解其工作原理和设计应用具有重要意义。

磁场强度的计算涉及到电流、线圈匝数、线径等多个因素。

以下是一些常见的计算方法：1.毕奥-萨伐尔定律：这是计算磁场强度的基本公式，特别是对于长直导线。

对于一个长度为l，流有电流I的导线，距离导线中心为r处的磁场强度H为：H = μ₀ × (I × l) / (4 × π × r^3)。

其中，μ₀是真空的磁导率。

2.安培定律：对于一个形状规则的线圈，例如矩形线圈，其磁场强度可以通过安培定律来计算。

假设线圈的匝数为n，流过的电流为I，线圈长度为l，宽度为w，距离线圈中心的距离为r，则H = μ₀ × n × I / (2 × π × r)。

3.磁感应强度：除了磁场强度H，另一个常用的参数是磁感应强度B。

对于长直导线，B的公式与H类似，只是分母中多了一个系数k：B = μ₀ × (I × l) / (4 × π × r^3 × k)。

对于线圈，B的计算公式与H类似，但需要考虑线圈的形状和方向。

4.磁路：在复杂的电磁系统，如电机、变压器等中，磁场强度可以通过磁路来计算。

磁路类似于电路，其中磁通量类似于电流，磁阻类似于电阻。

通过磁路的概念，可以更方便地理解和分析复杂的磁场分布。

5.有限元法：对于复杂的几何形状和磁场分布，可以使用有限元法进行计算。

这种方法将复杂的磁场问题分解为许多小的单元，每个单元都可以单独求解，然后将结果组合起来得到整体的磁场分布。

在设计和应用电磁铁时，需要综合考虑各种因素，如线圈匝数、电流、线径、气隙等，以确定最佳的磁场强度和分布。

同时，还需要考虑材料的磁导率和饱和磁感应强度等特性，以确保电磁铁的性能和稳定性。

直流电磁铁设计共26页编写： ______________________校对： _______________________直流电磁铁设计电磁铁是一种执行元件，它输入的是电能，输出的是机械能。

电能和机械能的变换是通过具体的电磁铁结构来实现的。

合理的电磁铁结构是能量变换效率提高的保证。

电磁铁设计的任务是合理的确定电磁铁的各种结构参数。

确定电磁铁的各种结构参数是一个相当复杂的任务，下面我们探讨确定电磁铁结构参数的一般方法。

电磁铁吸合过程是一个动态过程，设计是以静态进行计算.一、基本公式和一般概念1、均匀磁场B丄（T）S2、磁势F=NI,电流和匝数的乘积（A）3、磁场强度日二寻（A/m）,建立了电流和磁场的关系。

该公式适用于粗细均匀的磁路4、磁导率■二旦建立了磁场强度和磁感应强度（磁通密度）的关系 <H^=4 n X 10-7享/米相对磁导率r='-#05、磁通①二巴R M磁阻R M二+这称为磁路的欧姆定律，由于铁磁材料的磁导率卩不是常数，使用磁阻计算磁路并不方便，磁阻计算一般只用于定性。

真空中无限长螺线管B= — it °nl 。

2磁效率电磁铁工作循环图当电磁铁接上电源，磁力还不足克服反力，按0~2的直线进行磁化，达到期初始工作点2。

当磁力克服反力使气隙减小直至为零时, 工作点由2〜3。

断电后工作点由3〜0。

面积I 为断电后剩留的能量，面积H 为作功前电磁铁储存的能量，面积皿为电磁铁作的功6、磁感应强度的定义式 B=—,磁感应强度与力的关系。

qv7、 B=卩o nl 。

对于长螺线管，端面处的我们的目的是使I和H的面积最小，皿的面积最大。

面积I表示电磁铁作完功后的剩磁，（1）减小面积I可用矫顽力小的电铁。

（2）提咼制造精度，使吸合后气隙最小，但要防止衔铁粘住。

面积H表示作功前所储存的能量，在衔铁位置一定时，取决于漏磁通，漏磁通大，面积H就大。

9、机械效率K i=-AA0A :输出的有效功A0 :电磁铁可能完成的最大功10、重量经济性系数K2= —A0G=电磁铁重量。

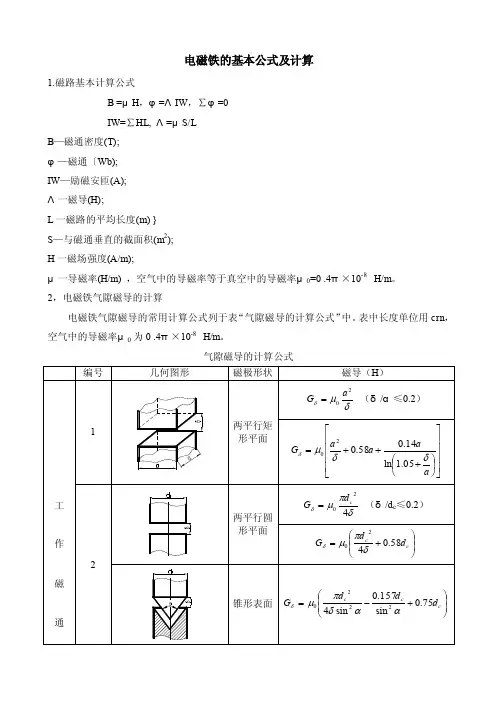
电磁铁的基本公式及计算1.磁路基本计算公式B =μH，φ=ΛIW，∑φ=0IW=∑HL, Λ=μS/LB—磁通密度(T);φ—磁通〔Wb);IW—励磁安匝(A);Λ一磁导(H);L一磁路的平均长度(m) }S—与磁通垂直的截面积(m2);H一磁场强度(A/m);μ一导磁率(H/m) ，空气中的导磁率等于真空中的导磁率μ0=0 .4π×10-8 H/m。

2，电磁铁气隙磁导的计算电磁铁气隙磁导的常用计算公式列于表“气隙磁导的计算公式”中。

表中长度单位用crn，空气中的导磁率μ0为0 .4π×10-8 H/m。

气隙磁导的计算公式3·电磁铁吸力基本计算公式 (1)计算气隙较小时的吸力为10210S392.0⨯=φF式中：F —电磁铁吸力(N)； φ—磁极端面磁通(Wb)； S —磁极表面的总面积(cm 2)。

(2)计算气隙较大时的吸力为10210)a S(1392.0⨯+=δφF式中：a —修正系数，约为3～5；δ—气隙长度（cm ）。

上式适用于直流和交流电磁铁的吸力计算。

交流时，用磁通有效值代入，所得的吸力为平均值。

例：某磁路如图所示。

已知气隙δ为0.04cm ，铁芯截面S 为4.4cm 2，线圈磁势IW 为1200安匝。

试求在气隙中所产生的磁通和作用在衔铁上的总吸力。

解：（1）一个磁极端面上的气隙磁导为000111004.04.4μμδμδ=⨯==S G 由于两个气隙是串联的，所以总磁导为G δ = G δ1/2=55μ0=55×0.4π×10-8=68.75×10-8（H ） (2)气隙中所产生的磁通为φδ=IW G δ =1 200×68.75×10-8 =8 .25×10-4 (Wb) (3)总吸力为)(1213104.425.8392.0210S 392.02102102N F =⨯⨯⨯=⨯⨯=δδφ 式中乘2是因为总吸力是由两个气隙共同作用所产生的。

直流电磁铁设计共26 页编写：校对：直流电磁铁设计电磁铁是一种执行元件，它输入的是电能，输出的是机械能。

电能和机械能的变换是通过具体的电磁铁结构来实现的。

合理的电磁铁结构是能量变换效率提高的保证。

电磁铁设计的任务是合理的确定电磁铁的各种结构参数。

确定电磁铁的各种结构参数是一个相当复杂的任务，下面我们探讨确定电磁铁结构参数的一般方法。

电磁铁吸合过程是一个动态过程,设计是以静态进行计算.一、基本公式和一般概念?（TB=） 1、均匀磁场S2、磁势F=NI,电流和匝数的乘积（A）NI（A/m），H=建立了电流和磁场的关系。

3、磁场强度L该公式适用于粗细均匀的磁路B建立了磁场强度和磁感应强度（磁通密度）的关系。

4、磁导率=?H?-7 = 10相对磁导率享/米×=4 π??r0?0NIΦ5、磁通=R M l =R磁阻M s这称为磁路的欧姆定律，由于铁磁材料的磁导率μ不是常数，使用磁阻计算磁路并不方便，磁阻计算一般只用于定性。

．F，磁感应强度与力的关系。

6、磁感应强度的定义式B=qv7、真空中无限长螺线管B=μnI。

对于长螺线管，端面处的01 nI。

B=μ0ψ2 8、磁效率当电磁铁接上电源，磁力还不足克服反力，按0～2的直线进行磁化，达到期初始工作点2。

当磁力克服反力使气隙减小直至为零时，工作点由2～3。

断电后工作点由3～0。

面积Ⅰ为断电后剩留的能量，面积Ⅱ为作功前电磁铁储存的能量，面积Ⅲ为电磁铁作的功。

．我们的目的是使Ⅰ和Ⅱ的面积最小，Ⅲ的面积最大。

面积Ⅰ表示电磁铁作完功后的剩磁，（1）减小面积Ⅰ可用矫顽力小的电铁。

（2）提高制造精度，使吸合后气隙最小，但要防止衔铁粘住。

面积Ⅱ表示作功前所储存的能量，在衔铁位置一定时，取决于漏磁通，漏磁通大，面积Ⅱ就大。

9、机械效率A =K1A0A：输出的有效功A0：电磁铁可能完成的最大功。

10、重量经济性系数G = K2A0G=电磁铁重量。

A0：电磁铁可能完成的最大功。

电磁铁计算公式电磁铁是一种利用电流产生磁场的装置，它在工业生产、科研实验和日常生活中都有着广泛的应用。

在设计和使用电磁铁时，我们需要了解一些相关的计算公式，以便能够准确地计算出所需的参数和性能。

本文将介绍一些常用的电磁铁计算公式，帮助读者更好地理解和应用电磁铁技术。

1. 计算电磁铁磁场强度的公式。

在电磁铁中，磁场强度是一个重要的参数，它决定了电磁铁的磁性能。

我们可以利用以下公式来计算电磁铁的磁场强度：H = (N I) / l。

其中，H表示磁场强度，单位是安培/米（A/m）；N表示匝数；I表示电流，单位是安培（A）；l表示磁路长度，单位是米（m）。

通过这个公式，我们可以根据电磁铁的匝数、电流和磁路长度来计算出电磁铁的磁场强度。

2. 计算电磁铁磁感应强度的公式。

磁感应强度是描述磁场强度的物理量，它也是电磁铁的重要性能指标。

我们可以利用以下公式来计算电磁铁的磁感应强度：B = μ0 μr H。

其中，B表示磁感应强度，单位是特斯拉（T）；μ0表示真空中的磁导率，其数值约为4π×10^-7 H/m；μr表示相对磁导率；H表示磁场强度。

通过这个公式，我们可以根据磁场强度和相对磁导率来计算出电磁铁的磁感应强度。

3. 计算电磁铁磁力的公式。

电磁铁的磁力是其另一个重要的性能指标，它决定了电磁铁在吸引和吸附物体时的力量大小。

我们可以利用以下公式来计算电磁铁的磁力：F = B S。

其中，F表示磁力，单位是牛顿（N）；B表示磁感应强度；S表示磁极面积，单位是平方米（m^2）。

通过这个公式，我们可以根据磁感应强度和磁极面积来计算出电磁铁的磁力大小。

4. 计算电磁铁电阻的公式。

在电磁铁中，电阻是一个重要的参数，它决定了电磁铁的电流和功率消耗。

我们可以利用以下公式来计算电磁铁的电阻：R = ρ (l / A)。

其中，R表示电阻，单位是欧姆（Ω）；ρ表示电阻率，单位是欧姆·米（Ω·m）；l表示电磁铁的长度，单位是米（m）；A表示电磁铁的横截面积，单位是平方米（m^2）。

直流电磁铁线圈匝数设计计算表摘要：一、引言1.1 背景介绍1.2 直流电磁铁的构成1.3 线圈匝数计算的重要性二、直流电磁铁线圈匝数计算方法2.1 磁场强度与导磁率的关系2.2 线圈匝数、电流和磁场强度的关系2.3 线圈材料选择2.4 线圈长度与匝数的关系2.5 线圈缠绕方向对磁性的影响三、线圈匝数设计步骤3.1 确定出力、行程、操作频率、工作电压等指标3.2 选择技术标准、铁磁材料和材料等级3.3 计算单位长度线圈匝数3.4 选择线圈缠绕层数3.5 确定线圈全长3.6 计算电磁铁长及直径四、直流电磁铁线圈匝数设计案例分析4.1 案例背景4.2 案例参数4.3 线圈匝数计算过程4.4 设计结果与分析五、结论5.1 线圈匝数计算对直流电磁铁性能的影响5.2 线圈匝数设计的注意事项5.3 对未来发展的展望正文：一、引言1.1 背景介绍直流电磁铁是一种将直流电能转化为磁场能的装置，其核心部分是线圈。

线圈匝数的设计直接影响到电磁铁的磁场强度、工作性能等方面，因此线圈匝数的计算是电磁铁设计中的重要环节。

1.2 直流电磁铁的构成直流电磁铁主要由线圈、铁芯和外壳组成。

线圈是电磁铁的核心部分，负责产生磁场；铁芯则负责承载磁场，增强磁效应；外壳主要用于保护内部元件和固定电磁铁。

1.3 线圈匝数计算的重要性线圈匝数的计算直接影响到直流电磁铁的磁场强度、工作性能等方面。

合理的线圈匝数设计可以提高电磁铁的工作效率、减小能耗、提高电磁铁的使用寿命。

二、直流电磁铁线圈匝数计算方法2.1 磁场强度与导磁率的关系磁场强度与导磁率成正比关系，即磁场强度= 导磁率× 电流。

2.2 线圈匝数、电流和磁场强度的关系线圈匝数、电流和磁场强度之间的关系可以表示为：磁场强度=匝数× 电流。

2.3 线圈材料选择线圈材料的选择会影响到线圈的电阻、导磁率等性能，因此需要根据实际需求选择合适的材料。

常见的线圈材料有铜、铝等。

2.4 线圈长度与匝数的关系线圈长度与匝数成正比关系，即线圈长度= 匝数× 单位长度。

电磁铁参数计算方式电磁铁参数计算方式(2012-02-17 11:00:53)标签:文化为确保您所使用的螺线管式电磁铁（包括我们通常所说的各式旋转电磁铁、推拉式电磁铁、直动式电磁铁、圆管式电磁铁等能可靠的工作和达到应有的寿命，我们在选用各种螺线管式电磁铁时，应注虑以下儿个方面:1、螺线管式电磁铁都是以直流电工作的，因此当工作电源为交流电时，请使用全波整流方式将交流电转换为直流电;2、通电率（或通电持续率），是用线圈通电时间和断开时间的比率来表技通时间示: 通电率"2 按逋时间+间断时间除通电率之外，有时还注出了每一次的最长通电时间的规定，这都是为防止线圈温度过度上升，从而导致螺线管电磁铁动作失误或寿命的减短，因此务必请在低于规定的数值下使用。

3、线圈中通过的电流值和线圈的圈数的乘积算做安培匝数。

各种螺线管式电磁铁的线圈数据中对应每个通电率周期都提供有参数值，螺线管式电磁铁的机械输出力的大小与其安培匝数成正比。

4、随着线圈温度的变化会引起螺线管电磁铁总体性能的变化。

当线圈接通电源施加上电圧后，线圈的温度会逐渐上升，线圈的电阻也就随之增加，通过线圈的电流会降低，从而，造成安培匝数的减少，螺线管电磁铁的机械输出功率也就变小。

一般产品样本或U录上所列的线圈数据和特性数据，均以环境温度20?时为依据，线圈温度和线圈电阻，安培匝数之间的关系如表1所示。

线圈温度(?)-40 -20 0 20 40 60 80 100 120 电阻系数0.764 0.843 0.921 1 1.079 1. 157 1.236 1.314 1.393 安培匝数比1.309 1.186 1.086 1 0.927 0. 864 0. 809 0. 761 0. 718 100% 50% 25% 10%线圈温升是按电器温升检测试验标准检测并以下式il•算确定式中:t：线圈温升(?)t：初始环1境温度(?)R：线圈初始电1阻(Q)t:最终环境温度(?)2R:线圈最终电阻(Q) 25、螺线管式电磁铁是一种带有高电感的电感负载，因此当通电电压断开时,控制用接点会产生电弧而被损坏，故应采取适当的接点保护措施。

电磁铁的设计计算电磁铁是一种利用电流的磁场产生磁力的设备，常用于工业制造、电子设备、电动机、磁悬浮等领域。

在设计电磁铁时，需要考虑电流、匝数、导线材料、磁路形状等因素。

下面我们将逐步介绍电磁铁的设计计算。

首先，我们需要确定电磁铁所需的磁力大小。

这取决于具体的应用需求，比如提起多大负荷、吸附多大物体等。

一般而言，磁力的大小与电流、匝数成正比。

其次，需要确定所用导线的截面积和电流。

根据所需磁力和电流，可以利用安培定律计算所需的导线长度。

安培定律表明，磁场力和电流成正比。

然后，需要计算所需的匝数。

匝数越多，则磁力越大。

计算匝数时，我们需要知道导线的长度以及每匝的长度。

导线长度可以根据安培定律和导线的电阻来计算。

每匝的长度可以通过所需的匝数和导线长度来计算。

接下来，需要确定导线材料。

导线材料的选择应考虑到电阻、耐热性和成本等因素。

常用的导线材料包括铜和铝。

铜导线的电阻较低且耐热性好，但成本较高，适合用于需要高功率输出的场合。

铝导线的电阻较高，但成本较低，适合用于一些低功率应用。

最后，需要设计电磁铁的磁路形状。

磁路形状影响着磁力的大小和分布。

常见的磁路形状有U型、C型、磁铁板型等。

选择合适的磁路形状可以提高磁力的利用率。

在设计电磁铁时，还需要考虑一些其他因素，比如电源电压、工作环境温度、散热等。

电源电压决定了电流的大小，工作环境温度和散热决定了电磁铁的容量和稳定性。

总之，电磁铁的设计计算是一个综合考虑电流、匝数、导线材料、磁路形状等因素的过程。

根据具体的应用需求，我们可以计算出所需的磁力大小，选择适当的导线和磁路形状，设计出满足要求的电磁铁。

筑
龙
网
W
W W
.Z
H U
L O
N G
.C
O M
直流电磁铁线圈的简化计算
在实际工作中，当绕制各种直流电磁铁时，需进行电磁系统计算。

这就涉及线圈导体截面、线圈匝数的计算。

一般都先假定取某一电流值，然后根据安匝数计算线圈匝数等值，最后校验电阻值是否能保证
假定的电流值。

这样，往往要反复多次，计算也比较麻烦。

现介绍一
种激磁安匝、铁芯尺寸一定时能直接计算激磁线圈应有的导线截面积
和匝数的简单方法。

设整个磁路磁势为F(A·N)，线圈尺寸如图3—6所示，宽b(m)，高h(m)，则线圈导体截面积A(mm 2
)和匝数N 的积与线圈断面积成比例，即：
bh=10-6
KAN (3—62)
式中的K 为导线的绕紧系数，与绕线工具、绕线技术等有关，一般取1.1~1.2。

导线中电流密度：J=FK／(bh)(A／m 2
) 则 b=FK／(Jh)
线圈中一匝导线的平均长度L(m)可用下列两式计算。

筑龙网
W
W W
.Z
H U
L O
N G
.C
O M
矩形铁芯时：
这样便可利用式(3—62)、(3—63)、(3—65)、(3—66)进行直流
电磁铁线圈的有关计算。

当需要改变某一数据时，通过分析可发现式
中哪一个参数收益更大(即敏感度分析)。

其不足之处是：绕紧系数K
与绕线工具、绕线技术等因素有关，其取值不当时，误差较大。

尤其
匝数较少时，误差更大些。

直流电磁铁线圈匝数设计计算表（实用版）目录一、引言1.1 背景介绍1.2 直流电磁铁的定义和应用1.3 线圈匝数计算的重要性二、直流电磁铁线圈匝数计算方法2.1 磁场强度和导磁率的概念2.2 线圈匝数计算公式2.3 线圈材料选择2.4 线径和层数的确定2.5 线圈全长和电磁铁尺寸的确定三、线圈匝数计算的实际应用案例3.1 应用背景和要求3.2 技术标准和材料选择3.3 线圈匝数计算过程3.4 实施结果和分析四、线圈匝数计算的挑战和展望4.1 计算过程中的不确定性4.2 线圈匝数计算的优化方向4.3 展望未来的发展趋势正文一、引言1.1 背景介绍电磁铁是一种利用电流在导线中产生的磁场来实现磁性吸附和释放的设备。

在工业生产和科学研究中，电磁铁被广泛应用于起重、牵引、制动、磁性材料加工等领域。

直流电磁铁是其中一种常见的类型，其磁性的强弱与线圈的匝数密切相关。

1.2 直流电磁铁的定义和应用直流电磁铁是指通过直流电流产生磁场的电磁铁。

与交流电磁铁相比，直流电磁铁的磁场稳定性更好，因此在一些需要稳定磁场的应用场景中更为常见。

例如，在磁性材料加工、永磁电机等领域，直流电磁铁被广泛使用。

1.3 线圈匝数计算的重要性线圈匝数是影响直流电磁铁磁性强弱的重要因素。

合理的线圈匝数设计可以提高电磁铁的磁性能，从而实现更高效的磁性吸附和释放。

因此，对直流电磁铁线圈匝数进行科学计算具有重要的实际意义。

二、直流电磁铁线圈匝数计算方法2.1 磁场强度和导磁率的概念磁场强度是指单位面积上通过的磁力线数量，单位为安培/米（A/m）。

导磁率是指材料在磁场中的磁化程度，单位为亨利每米（H/m）。

2.2 线圈匝数计算公式线圈匝数的计算公式为：N = (B * H) / (μ * I)，其中 N 为线圈匝数，B 为磁场强度，H 为导磁率，μ为线圈材料的相对磁导率，I 为线圈中的电流。

2.3 线圈材料选择线圈材料的选择会影响电磁铁的磁性能。

一般而言，导磁率越高的材料，其磁性能越好。

电磁铁吸力计算一、按所给参数要求计算：已知：工作电压：U=12V 电阻：R=285±10% 匝数：W=3900 线径：Φ0.08由已知条件可计算得出：电流：I=U/R=12/285=0.042A安匝值：IW=0.042*3900=163.8电磁吸力：F=2)5000(Φ*)1(1αδ+S (1)其中: Φ：通过铁芯极化面的磁通量MxS ：为铁心极化面面积2cmδ：未吸合时衔铁和铁芯的气隙长度cmα：修正系数,一般在3～4之间,在此取其中间值4=α在式(1)中磁通量为:Φ=810**δG IW (2)其中: IW ：线包的安匝值δG ：工作磁通的磁导H在式(2)中工作磁通的磁导为:δG =)11(222020R rR --δμπ (3)其中: 0R ：衔铁旋转位置到铁芯中心的长度cm0μ：空气中的磁导率为0.4π*108-cm H /r ：极化面的半径cm由产品结构图可知：0R =0.56 r=0.3 δ=0.069故有:δG =)56.03.011(069.010*4.0*56.0*22282---ππ=5.58*108-Φ=8810*10*58.5*8.163-=914F=)069.0*41(3.0*1*)5000914(22+π=0.093Kgf =93gf二、改进后吸力计算改进方案1:改用Φ0.09线，绕制后所得匝数为W=4262,其他参数不变，故：安匝值 IW=0.042*4262=179则：Φ=8810*10*58.5*179-=998.82F=)069.0*41(3.0*1*)500082.998(22+π=0.111Kgf =111gf改进方案2:将线包功率增加到0.7W 则其电阻值变为：Ω===7.2057.01222PU RA RU I 058.07.20512===此时绕制后所得匝数为W=3361 ,其他参数不变故有：安匝值 IW=0.058*3361.34=194.94Φ=8810*10*58.5*94.194-=1087.77F=)069.0*4.01(3.0*1*)500077.1087(22+π=0.131Kgf =131gf三、可靠性改进：A 、零件一次性的控制（轭铁一模一出/铁芯冷镦一模一出/骨架一模重新开模）B 、铁芯铰锭一次性的控制 设计治具C 、取消铁芯帖纸抬高释放，衔铁重新设计抬高释放。

电磁铁吸力的有关公式这里的所有的对象都应该是铁.1.F=B^2*S/(2*u0) 此式中,F=焦耳/厘米,B=韦伯/平方厘米,S= 平方厘米该式改变后成为:F=S*(B/5000)^2 此式中,F=Kg,B=高斯,S= 平方厘米当加入气隙后,F=(S*(B/5000)^2)/(1+aL) a是一个修正系数,一般是3--5,L是气隙长度.2.F=u0*S0*(N*i)^2/8(L^2)S0:空气隙面积 m^2N :匝数i :电流L :气隙长度3.F=(B^2*S*10^7)/(8*PI) 这个式子和第一个式子是相等的.当不存在气隙的时候,就应该是电磁铁在端面处所产生的力.1. u0就是μ0吧？2. 有这句话：“当加入气隙后...”，就意味着，原公式不是针对“空心线圈”？是吗？3. 我的理解是：上述公式是应用于“气隙比较于磁链长度相对较短的铁心线圈”。

如果不是针对"空心线圈",那么线圈内部的材质是什么呢?能在公式的哪里体现出来?应该在B里面体现出来.那么,我们是否可以这样做个假定,来匹配现在的情况?假定,悬浮体是一个通电圆导线,电流I,半径R.匀强磁场B垂直通过其所在平面.那么它所受到的力应该如何计算?由通电圆导线所形成的磁场,是否可以类比于悬浮磁体?假设电流I足够大,两者的半径R相等,从而达到两者所在平面的磁感应强度相等.那你的意思是：上述公式是针对"空心线圈"？若是，气隙如何定义？你的这个思路非常有趣。

让我慢慢来画一个图，配合这个思路。

(原文件名:思路非常有趣1.JPG)引用图片是这个意思吧？差不多就是这个意思.只不过两个线圈所产生的B不一样.而且右边线圈的半径要小于左边的线圈.作为第一步，我们可以将题目中的“磁铁”改成“铁块”，“电磁线圈”改成“无铁心电磁线圈”。

----------------------------------------------这样似乎更复杂了，因为“铁块”是被电磁线圈磁化产生磁性，才和电磁线圈产生力的，那“铁块被磁化”如何量化？下面说说我找的资料：库仑磁力定律：(原文件名:18864f550ffc2c29f8b9d79da17f2fa2.png)引用图片其中m1 m2是两个磁极的磁通量，单位韦伯，d是两磁极距离。

电磁力与磁场强度的公式关系
电磁铁电磁力计算公式磁场强度的计算公式：H = N × I / Le 式中：H为磁场强度，单位为A/m；N为励磁线圈的匝数；I为励磁电流（测量值），单位位A；Le为测试样品的有效磁路长度，单位为m。

磁感应强度计算公式：B = Φ / (N × Ae)
式中：B为磁感应强度，单位为Wb/m^2；Φ为感应磁通（测量值），单位为Wb；N为感应线圈的匝数；Ae为测试样品的有效截面积，单位为m^2。

磁场的电磁力的大小与磁感应强度、导体内的电流、导体的长度以及电流与磁场方向间的夹角都有关系，在均匀磁场中，他们之间的关系可用以下公式表示为F=BILsinaθ：上面的公式就是电磁力公式，式中各个参数分表代表的含义是：F：表示导体在磁场中所受的电磁力，单位（N）B：表示磁场的磁感应强度，单位（T，简称“特”）I：表示导体内的电流，单位（A）L：表示磁场中的导体长度，单位（m）θ：表示磁感应强度方向与
磁场的电磁力的大小与磁感应强度、导体内的电流、导体的长度以及电流与磁场方向间的夹角都有关系，在均匀磁场中，他们之间的关系可用以下公式表示为F=BILsinaθ。