【东南大学】《几何与代数》总复习资料共56页文档

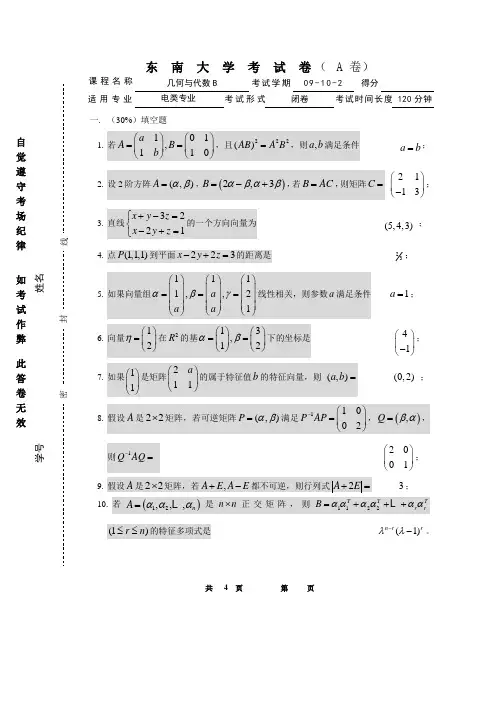
共 4 页 第 页东 南 大 学 考 试 卷（ A 卷）课程名称 几何与代数B 考试学期09-10-2得分适用专业电类专业考试形式闭卷考试时间长度 120分钟一. （30%）填空题1. 若101,110a A B b ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭，且222()AB A B =，则,a b 满足条件 a b =；2. 设2阶方阵(,)A αβ=，()2,3B αβαβ=-+，若B AC =，则矩阵C = 2113⎛⎫⎪-⎝⎭；3. 直线3221x y z x y z +-=⎧⎨-+=⎩的一个方向向量为 (5,4,3) ；4. 点(1,1,1)P 到平面223x y z -+=的距离是23；5. 如果向量组1111,,21a a a αβγ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭线性相关，则参数a 满足条件 1a =；6. 向量12η⎛⎫= ⎪⎝⎭在2R 的基13,12αβ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭下的坐标是 41⎛⎫ ⎪-⎝⎭；7. 如果11⎛⎫ ⎪⎝⎭是矩阵211a ⎛⎫⎪⎝⎭的属于特征值b 的特征向量，则 (,)a b = (0,2) ； 8. 假设A 是22⨯矩阵，若可逆矩阵(,)P αβ=满足11002P AP -⎛⎫=⎪⎝⎭，(),Q βα=，则1Q AQ -= 2001⎛⎫⎪⎝⎭；9.(1)r n ≤≤的特征多项式是 (1)n r r λλ--。

共 4 页 第 页二. （10%）设211101111A ⎛⎫⎪= ⎪ ⎪⎝⎭，111012B -⎛⎫= ⎪⎝⎭。

已知XA B X =+ ，求 X 。

解：()X A E B -=，1()X B A E -=-， (4)111111110A E ⎛⎫ ⎪-=- ⎪ ⎪⎝⎭，1122111221()0101A E --⎛⎫ ⎪-=- ⎪ ⎪-⎝⎭， (4)51220102X ⎛⎫= ⎪--⎝⎭……………………………………………………………………2 三. （14%）设线性方程组12342341234123412123435(6)5x x x x x x x x x ax x b x x x a x + + +=⎧⎪ - +=⎪⎨+ + +=⎪⎪+ +++=⎩。

代数与几何基础第一章：行列式和消元法1。

行列式det，对角线法则，主对角线，次对角线；第1页2。

n阶排列，逆序，逆序数，奇排列，偶排列，自然排列；第2页3。

上三角行列式，对角行列式；第4页4。

转置行列式；第8页5。

行列式的展开，vandermonde行列式；6。

行列式的子式，余子式，代数余子式；第15页7。

行列式的分解，Laplace定理；第16页8。

线形方程组，齐次/非齐次线形方程组，解集合，通解，相容/不相容；第21页9。

N元线形方程组的求解，cramer法则；第22页10。

多项式插值--根据采样值求函数；第25页11。

消元法，线形方程组的初等变换；第27页12。

矩阵，元，复矩阵，方阵，零矩阵O，单位矩阵E，同型矩阵，系数矩阵，增广矩阵，矩阵初等变换；第29页13。

矩阵的子式，方阵的行列式，矩阵的秩/rank，行满秩矩阵，列满秩矩阵，非奇异矩阵，奇异矩阵，首元，梯矩阵，行最简矩阵；第31页14。

矩阵的等价标准形；第33页15。

自由未知量--因方程数不够而多出来的无法求解的未知量；第35页第二章：几何向量及应用1。

向量的长度/模/范数；第39页2。

自由向量，径向量/径矢/向径，负向量，向量的共线/平行，正交/垂直，向量三角形加法法则，向量的数乘，向量的线形运算；第40页3。

空间仿射坐标系，右手坐标系，左手坐标系，仿射坐标；第46页4。

空间直角坐标系，横坐标，纵坐标，竖坐标，8个卦限及顺序；第48页5。

向量的标量积/内积，向量之间的投影prj；第49页6。

标量积运算特性；第50页7。

向量的方向余弦，方向角；第52页8。

向量的向量积/叉积，平行四边形法则，向量积运算特性；第53页9。

向量积在空间直角坐标系中的行列式表达；第54页10。

向量的混合积，平行六面体体积法则；第55页11。

混合积运算法则；第56页12。

法向量，点法式方程，平面的一般式方程--3元一次方程；第58页13。

平面3点式方程的行列式表达，平面的截距式方程，截距；第59页14。