东南大学田玉平自动控制原理参考答案4

4.1 对于如下系统，求其传递函数。

并判别：系统是否由其传递函数完全表征？系统是否渐进稳定？是否输入-输出稳定？（1）[]0100001061161310x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦= 解：由3261160sI A s s s -=+++=得极点为：1231,2,3s s s =-=-=-所以系统渐进稳定。

13231()()6116(1)(2)s G s C sI A B s s s s s -+=-==+++++ 所以系统为输入-输出稳定，但不能由G （s ）完全表征。

（2）[]010000102500550510x x u y x⎡⎤⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦=-解：由3252500sI A s s -=+-=得1235,55,55s s i s i ==-+=--所以不是渐进稳定。

G(s)=C(sI-A)1-B=C 1502501001-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---s s sB=)5)(55)(55()5(50--+++-s j s j s s .=)55)(55(50j s j s -+++所以系统是输入-输出稳定，但不能由G （s ）完全表征。

（3）[]110001010002110x x u y x-⎡⎤⎡⎤⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=- 解：由3220sI A s s s -=++=得1230,1,1s s s ==-=-所以系统不是渐进稳定。

12()()(1)sG s C sI A B s --=-=+ 所以系统是输入-输出稳定，但不能由G （s ）完全表征。

（4）（a ）解：25()27s G s s s -=+-，1,21s =-± 所以既不是渐进稳定，又不是输入-输出稳定。

系统可由其传递函数完全表征。

.（b ）解：)54)(1()1)(3()(2++-++=s s s s s S G .，有极点在右半平面所以既不是渐进稳定，又不是输入-输出稳定。

第1章控制系统概述【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统，说明它们的工作原理并比较开环控制和闭环控制的优缺点。

解：开环控制——半自动、全自动洗衣机的洗衣过程。

工作原理：被控制量为衣服的干净度。

洗衣人先观察衣服的脏污程度，根据自己的经验，设定洗涤、漂洗时间，洗衣机按照设定程序完成洗涤漂洗任务。

系统输出量（即衣服的干净度）的信息没有通过任何装置反馈到输入端，对系统的控制不起作用，因此为开环控制。

闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。

工作原理：以卫生间蓄水箱蓄水量控制为例，系统的被控制量（输出量）为蓄水箱水位（反应蓄水量）。

水位由浮子测量，并通过杠杆作用于供水阀门（即反馈至输入端），控制供水量，形成闭环控制。

当水位达到蓄水量上限高度时，阀门全关（按要求事先设计好杠杆比例），系统处于平衡状态。

一旦用水，水位降低，浮子随之下沉，通过杠杆打开供水阀门，下沉越深，阀门开度越大，供水量越大，直到水位升至蓄水量上限高度，阀门全关，系统再次处于平衡状态。

开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成各个环节分别的作用是什么解：自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。

各个基本单元的功能如下：（1）被控对象—又称受控对象或对象，指在控制过程中受到操纵控制的机器设备或过程。

（2）给定元件—可以设置系统控制指令的装置，可用于给出与期望输出量相对应的系统输入量。

（3）检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量，再反馈到系统输入端作比较，一般为各类传感器。

（4）比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较，分析计算并产生反应两者差值的偏差信号。

常用的比较元件有差动放大器、机械差动装置和电桥等。

（5）放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时，可通过放大元件将微弱信号作线性放大。

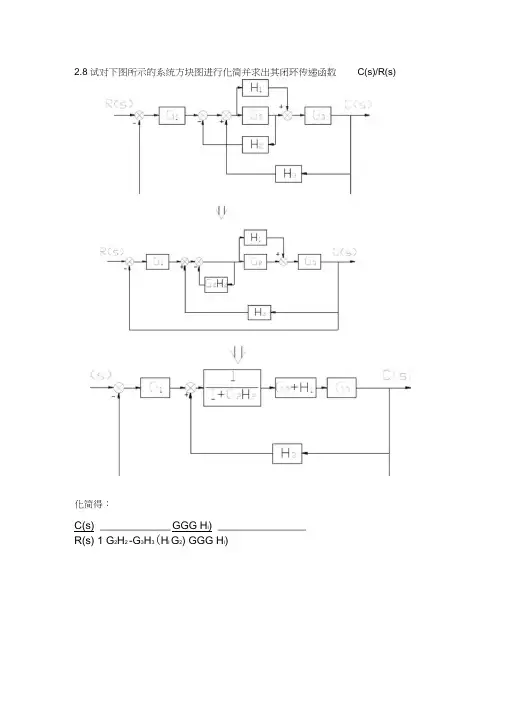
2.8试对下图所示的系统方块图进行化简并求出其闭环传递函数C(s)/R(s)化简得：C(s) ____________ GGG H i) _______________R(s) 1 G2H2 -G3H3(H i G2) GGG H i)2.9化简得：C(s) G1G2G3G4丽-(1 GH i)(1 G4H4MI G2H2X I G3H3) G2G3H5] GG2G3G4H62.10求信号流图的传递函数（a）解：有6个前向通道：Q i（s） =GGG7Q2（S）二GGG8Q3（S）二G2G4G8Q4（S）二G2G5G7Q5（s）二-GGH2G5G7Q e（s）八G2G5HGG8共有三个回路，分别为：L,(s)八G3H1L2(s) = -G4H2L_3(S)=G5G6H I H2(s^1 G3H1 G4H^G5G6H1H2 G3H1G4H2,s） =1 G4H22（s） -13（S）- 1 G3H14（S） =15（S） =16（S）=1GQG7（1 G4H2） GGA QG q G g。

G3H1） G2G5G - GQH2G5G7 - G2G5H1GJG8 G （s）-1+G3H<H G4H^G5G6H1H<H G3H1G4H2（b）共有4条前向通道，分别为：Q i（s） = G1G2G3G4G5G6Q2（S）二G3G4G5G6Q3（s）二GGQ4（S）八G e H i共有9条回路，分别为：L|（s）二-G?H iL2（s） = - G4 H 2L3G）八GetL4（s） = -G3G4G5H4L5G）八GG2G3G4G5G6H5Q（s）十出（ s） - - G3G4G5G6 H5L7L B（S）二H1H5G6L9（s^ -G6H5G1（s） =1 G2H1 G4H2 G6H3 G1G2G3G4G5G6H5 G2H1G4H2G2HGH3 G4H2G6H3 G2H1G4H2G6H3 -H i H4 G3G4G5G6H5-G1H5G6 G6H5G -G q H z H i H s G e G4H2GH5G6-G4H2H i H4、1(S)=12(S)=1、3(S)=1 G4H2、4(S)=1 G4H2G1G2G3G4G5G6 G3G4G5G6 G1G6(1 G4H2)- G6H1(1 G4H2)(s)(c)共有2条前向通路，分别是:Q[(s) =abcdQ2(s)二aed共有6条回路，分别是：J(s)二bgL2(s) =chL3G) = fL4(s) =kbcl_5(s)二keL s(s)二eghabed + aed(1- f)1 - bg - ch - f - kbc - ke - egh kfe(d)有4条前向通道，分别是:Q1 (s)二adeQ2(s)二aQ3(s)二bcdeQ4(s)二bc有4条回路，分别是：LJs)「-cfL2(s)八egR(s)「-adehL4(s)「-bcdehade a aeg bcde be bceg G(S)- 1 + cf + eg + adeh + bcdeh+ cfeg G(s)-1 +G1G 3H 1H ^G 1G 2H 1H 22.13画出极坐标图，求与实轴相交的频率和相应的幅值。

【课后自测】1-1 试列举几个日常生活中的开环控制和闭环控制系统，说明它们的工作原理并比较开环控制和闭环控制的优缺点。

解：开环控制——半自动、全自动洗衣机的洗衣过程。

工作原理：被控制量为衣服的干净度。

洗衣人先观察衣服的脏污程度，根据自己的经验，设定洗涤、漂洗时间，洗衣机按照设定程序完成洗涤漂洗任务。

系统输出量（即衣服的干净度）的信息没有通过任何装置反馈到输入端，对系统的控制不起作用，因此为开环控制。

闭环控制——卫生间蓄水箱的蓄水量控制系统和空调、冰箱的温度控制系统。

工作原理：以卫生间蓄水箱蓄水量控制为例，系统的被控制量（输出量）为蓄水箱水位（反应蓄水量）。

水位由浮子测量，并通过杠杆作用于供水阀门（即反馈至输入端），控制供水量，形成闭环控制。

当水位达到蓄水量上限高度时，阀门全关（按要求事先设计好杠杆比例），系统处于平衡状态。

一旦用水，水位降低，浮子随之下沉，通过杠杆打开供水阀门，下沉越深，阀门开度越大，供水量越大，直到水位升至蓄水量上限高度，阀门全关，系统再次处于平衡状态。

开环控制和闭环控制的优缺点如下表1-2 自动控制系统通常有哪些环节组成？各个环节分别的作用是什么？解：自动控制系统包括被控对象、给定元件、检测反馈元件、比较元件、放大元件和执行元件。

各个基本单元的功能如下：（1）被控对象—又称受控对象或对象，指在控制过程中受到操纵控制的机器设备或过程。

（2）给定元件—可以设置系统控制指令的装置，可用于给出与期望输出量相对应的系统输入量。

（3）检测反馈元件—测量被控量的实际值并将其转换为与输入信号同类的物理量，再反馈到系统输入端作比较，一般为各类传感器。

（4）比较元件—把测量元件检测的被控量实际值与给定元件给出的给定值进行比较，分析计算并产生反应两者差值的偏差信号。

常用的比较元件有差动放大器、机械差动装置和电桥等。

（5）放大元件—当比较元件产生的偏差信号比较微弱不足以驱动执行元件动作时，可通过放大元件将微弱信号作线性放大。

自控原理试卷(11-12)标准答案一、简答题1、开环控制系统无反馈回路，结构简单，成本较低，但是控制精度低，容易受到外界干扰，输出出现误差无法进行补偿；闭环控制结构相对复杂，但能在有不可预知的干扰的情况下，使得输出量和参考输入量之间的偏差尽可能小。

2、如果系统开环传递函数在右半平面没有零、极点，那么该系统为最小相位系统； 有延迟环节的系统不属于最小相位系统。

3、一个连续时间线性定常系统输入-输出稳定的充分必要条件是其微分方程的特征方程的根（即传递函数的极点）全部具有负的实部。

4、存在矛盾之处，三阶系统例子。

5、状态反馈不会改变系统的能控性，输出反馈也不会改变系统的能控性； 输出反馈不会改变系统的能观性，状态反馈有可能改变系统的能观性。

二、综合题1、 13223232143211s (H G G H G G G G G G G G G G -++=）2、 解： ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=11126621641k Q 验证：0=k Q ，可以知道n rankQ k <，所以系统不完全可控。

⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=1016104101g Qn rankQ k <=2 系统不完全可观3、 解：由已知条件可知91=a ，52=a ，33=a ，00=b ，11=b ，42=b ，13=b 选取状态变量 y x =1,y x =2,yx =3, 则 00=β，11=β，52-=β，413=β于是得到系统状态空间表达式为u X X ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=4151953100010 []X y 001= 4、26313,2js ±=，12=K5、⎥⎦⎤⎢⎣⎡+-+---=-=-t t tt t t tt e e e e e e e e t t 222212222)()(ΦΦ6、系统的闭环传递函数为Ks s s s Ks R s C ++++=)2)(1()()(2所以系统的特征方程为D （s ）=0233234=++++K s s s s 劳斯表如下：Ks K s Ks s Ks 01234792372331-需满足：0792,0>->kK解得系统闭环稳定的K 的取值范围为：0<K<14/97、①6,5,3321-=-=-=λλλ；②-A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=6-5-3-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-3/12/16/1B。

第一章 绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答：1开环系统(1) 优点:结构简单,成本低,工作稳定;用于系统输入信号及扰动作用能预先知道时,可得到满意的效果;(2) 缺点：不能自动调节被控量的偏差;因此系统元器件参数变化,外来未知扰动存在时,控制精度差;2 闭环系统⑴优点：不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值,都会产生控制作用去清除此偏差,所以控制精度较高;它是一种按偏差调节的控制系统;在实际中应用广泛;⑵缺点：主要缺点是被控量可能出现波动,严重时系统无法工作;1-2 什么叫反馈为什么闭环控制系统常采用负反馈试举例说明之;解答：将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈;闭环控制系统常采用负反馈;由1-1中的描述的闭环系统的优点所证明;例如,一个温度控制系统通过热电阻或热电偶检测出当前炉子的温度,再与温度值相比较,去控制加热系统,以达到设定值;1-3 试判断下列微分方程所描述的系统属于何种类型线性,非线性,定常,时变122()()()234()56()d y t dy t du t y t u t dt dt dt ++=+ 2()2()y t u t =+3()()2()4()dy t du t ty t u t dt dt +=+ 4()2()()sin dy t y t u t t dt ω+= 522()()()2()3()d y t dy t y t y t u t dt dt ++=62()()2()dy t y t u t dt +=7()()2()35()du t y t u t u t dtdt =++⎰解答： 1线性定常 2非线性定常 3线性时变 4线性时变 5非线性定常 6非线性定常7线性定常1-4 如图1-4是水位自动控制系统的示意图,图中Q1,Q2分别为进水流量和出水流量;控制的目的是保持水位为一定的高度;试说明该系统的工作原理并画出其方框图;题1-4图 水位自动控制系统解答：1 方框图如下：⑵工作原理：系统的控制是保持水箱水位高度不变;水箱是被控对象,水箱的水位是被控量,出水流量Q2的大小对应的水位高度是给定量;当水箱水位高于给定水位,通过浮子连杆机构使阀门关小,进入流量减小,水位降低,当水箱水位低于给定水位时,通过浮子连杆机构使流入管道中的阀门开大,进入流量增加,水位升高到给定水位;1-5 图1-5是液位系统的控制任务是保持液位高度不变;水箱是被控对象,水箱液位是被控量,电位器设定电压时表征液位的希望值Cr 是给定量;题1-5图 液位自动控制系统解答:1 液位自动控制系统方框图：2当电位器电刷位于中点位置对应Ur 时,电动机不动,控制阀门有一定的开度,使水箱中流入水量与流出水量相等;从而液面保持在希望高度上;一旦流入水量或流出水量发生变化,例如当液面升高时,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一事实上的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液位流量减少;此时,水箱液面下降,浮子位置相应下降,直到电位器电刷回到中点位置,系统重新处于平衡状态,液面恢复给定高度;反之,若水箱液位下降,则系统会自动增大阀门开度,加大流入量,使液位升到给定的高度;1-6题图1-6是仓库大门自动控制系统的示意图,试说明该系统的工作原理,并画出其方框图;题1-6图仓库大门自动控制系统示意图解答：（1）仓库大门自动控制系统方框图：2工作原理：控制系统的控制任务是通过开门开关控制仓库大门的开启与关闭;开门开关或关门开关合上时,对应电位器上的电压,为给定电压,即给定量;仓库大门处于开启或关闭位置与检测电位器上的电压相对应,门的位置是被控量;当大门所处的位置对应电位器上的电压与开门或关门开关合上时对应电位器上的电压相同时,电动机不动,控制绞盘处于一定的位置,大门保持在希望的位置上,如果仓库大门原来处于关门位置,当开门开关合上时,关门开关对应打开,两个电位器的电位差通过放大器放大后控制电动机转动,电动机带动绞盘转动将仓库大门提升,直到仓库大门处于希望的开门位置,此时放大器的输入为0,放大器的输出也可能为0;电动机绞盘不动,大门保持在希望的开门位置不变;反之,则关闭仓库大门;1-7题图1-7是温湿度控制系统示意图;试说明该系统的工作原理,并画出其方框图;题1-7图温湿度控制系统示意图解答：1方框图：2被控对象为温度和湿度设定,控制任务是控制喷淋量的大小来控制湿度,通过控制蒸汽量的大小来控制温度;被控量为温度和湿度,设定温度和设定湿度为给定量;第二章 控制系统的数学模型2-2 试求图示两极RC 网络的传递函数U c S ／U r S;该网络是否等效于两个RC 网络的串联解答：故所给网络与两个RC 网络的串联不等效;2-4 某可控硅整流器的输出电压U d =KU 2Φcos α式中K 为常数,U 2Φ为整流变压器副边相电压有效值,α为可控硅的控制角,设在α在α0附近作微小变化,试将U d 与α的线性化;解答：.202002020cos (sin )()...sin sin )d u ku ku ku ku φφφφαααααααα=--+∆=-⋅∆=-d d 线性化方程：u 即u （2-9系统的微分方程组为式中1T 、2T 、1K 、2K 、3K 均为正的常数,系统地输入量为()r t ,输出量为()c t ,试画出动态结构图,并求出传递函数()()C s R s ; 解答：2-12 简化图示的动态结构图,并求传递函数()()C s R s ; 解答：ab c d e2-13 简化图示动态结构图,并求传递函数()()C s R s ;解答： a bcde(d)f第三章 时域分析法3-1 已知一阶系统的传递函数今欲采用负方馈的方法将过渡过程时间s t 减小为原来的倍,并保证总的放大倍数不变,试选择H K 和0K 的值;题3-1图解答：闭环传递函数：10()0.2110s s θ=+由结构图知：00010()10110()0.21()0.21101110HHh HK k G S k K s K G S s k S K θ+===+++++由00101011011010100.910H H H k k k k k ⎧⎪⎪⎨⎪⎪⎩⎧⎪⎨⎪⎩=++===3-2已知系统如题3-2图所示,试分析参数b 对输出阶跃过渡过程的影响;题3-2 图解答：系统的闭环传递函数为：由此可以得出：b 的大小影响一阶系统的时间常数,它越大,系统的时间常数越大,系统的调节时间,上升时间都会增大;3-3 设温度计可用1(1)Ts +描述其特性;现用温度计测量盛在容器内的水温,发现1分钟可指示98％的实际水温值;如果容器水温依10℃/min 的速度线性变化,问温度计的稳态指示误差是多少解答：本系统是个开环传递函数 系统的闭环传递函数为：系统的传递函数：1()1G s Ts =+则题目的误差传递函数为：3-4 设一单位反馈系统的开环传递函数试分别求110K s -=和120K s -=时系统的阻尼比ζ、无阻尼自振频率n w 、单位阶跃响应的超调量p σ％和峰值时间p t ,并讨论K 的大小对动态性能的影响;解答：开环传递函数为3-8 设控制系统闭环传递函数试在s 平面上给出满足下列各要求的闭环特征根可能位于的区域： 1. 10.707,2n ζω>≥≥ 2. 0.50,42n ζω≥>≥≥ 3. 0.7070.5,2n ζω≥≥≤解答：欠阻尼二阶系统的特征根：1. 由0.7071,arccos ζβζ<<=,得045β︒︒<≤,由于对称关系,在实轴的下半部还有;2. 由00.5,arccos ζβζ<≤=,得6090β︒︒≤<,由于对称关系,在实轴的下半部还有;3. 由0.50.707,arccos ζβζ≤≤=,得出4560β︒︒≤≤,由于对称关系,在实轴的下半部还有;则闭环特征根可能位于的区域表示如下：1． 2． 3．3-10 设单位反馈系统开环传递函数分别为： 1.[]()(1)(0.21)G s K s s s =-+2. ()(1)[(1)(0.21)]G s K s s s s =+-+ 试确定使系统稳定的K 值;解答：1.系统的特征多项式为：()D s 中存在特征多项式中存在负项,所以K 无论取什么值,系统都不会稳定;2.系统的特征多项式为：32()0.20.8(1)D s s s k s k =++-+ 劳斯阵列为：3s k-12s k 0s k系统要稳定 则有 0.60.800.80k k ⎧⎪⎨⎪⎩->>所以系统稳定的K 的范围为43k >3-14 已知单位反馈系统开环传递函数如下： 1.]()10(0.11)(0.51)G s s s =++2.2()7(1)(4)(22)G s s s s s s ⎡⎤=++++⎣⎦ 3.2()8(0.51)(0.11)G s s s s ⎡⎤=++⎣⎦ 解答:1.系统的闭环特征多项式为: 可以判定系统是稳定的.则对于零型系统来说,其静态误差系数为:那么当()1()r t t =时, 11111ss p e k ==+当()1()r t t t =⋅时, 1ss ve k ==∞当2()1()r t t t =⋅时, 2ss ae k ==∞2.系统的闭环特征多项式为: 可以用劳斯判据判定系统是稳定的. 则对于一型系统来说,其静态误差系数为:那么当()1()r t t =时, 11ss p e k ==∞+ 当()1()r t t t =⋅时,187ss v e k ==当2()1()r t t t =⋅时, 20ss ae k ==3.系统的闭环特征多项式为: 可以用劳斯判据判定系统是稳定的. 则对于零型系统来说,其静态误差系数为:那么当()1()r t t =时, 11ss p e k ==+ 当()1()r t t t =⋅时, 10ss v e k ==当2()1()r t t t =⋅时, 214ss a e k ==第四章 根轨迹法4-2 已知单位反馈系统的开环传递函数,绘出当开环增益1K 变化时系统的根轨迹图,并加以简要说明;1.1()(1)(3)K G s s s s =++2.12()(4)(420)K G s s s s s =+++解答:1 开环极点： p1=0,p2=－1,p3=－3实轴上的根轨迹区间： －∞,－3,－1,0 渐进线：分离点：111013d d d ++=++解得d1、2=－,;d2=－不在根轨迹上,舍去; 与虚轴交点：特征方程321()430D s s s s K =+++= 将s =j ω代入后得解之得 ω= 112K =当 ∞<≤10K 时,按180相角条件绘制根轨迹如图4-21所示;2 开环极点：p1=0,p2=－4,p3、4=－2±j4实轴上的根轨迹区间：－4,0 渐进线：分离点：)8018368(2341++++-=s s s s K 由01=ds dK解得 s1、2=－2,624,3j s ±-= 分离点可由a 、b 、c 条件之一进行判定：a ．∠Gs 3=－129o+51o －90o+90o=－180o,满足相角条件；b ．100)80368()(62234313>=+++-=+-=j s s s s s s KK 1在变化范围 )0[∞→ 内；c ．由于开环极点对于σ=－2直线左右对称,就有闭环根轨迹必定也是对于σ=－2直线左右对称,故s3在根轨迹上;与虚轴交点： 特征方程Routh 表s 4 1 36 K 1 s 3 8 80 s 2 26 K 1 s 80－8K1/26 s 0 K 1由 80－8k1/26=0和26s2+ k1=0,解得k1=260,102,1j s ±= ;当 ∞<≤10K 时,按180相角条件绘制根轨迹如图4－22所示;4-3 设单位反馈系统的开环传递函数为（1） 试绘制系统根轨迹的大致图形,并对系统的稳定性进行分析;、（2） 若增加一个零点1z =-,试问根轨迹有何变化,对系统的稳定性有何影响解答1 K 1>0时,根轨迹中的两个分支始终位于s 右半平面,系统不稳定；2 增加一个零点z=－1之后,根轨迹左移,根轨迹中的三个分支始终位于s 左半平面,系统稳定;4-4 设系统的开环传递函数为12(2)()()(2)K s G s H s s s s a +=++,绘制下列条件下的常规根轨迹;11a =； 2 1.185a = 33a =解答： 11=a实轴上的根轨迹区间： －∞,－1,－1,0 渐进线：分离点：22231+++-=s as s s K解得01=ds dK只取253+-=d ;与虚轴交点：特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式：得出与虚轴的交点系统的根轨迹如下图： 2185.1=a 零点为2-=z极点为0,43.01j p ±-=实轴上的根轨迹区间： －∞,－1,－1,0 渐进线：分离点：22231+++-=s as s s K解得01=ds dK特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式：得出与虚轴的交点系统的根轨迹如下图： 33=a 零点为2-=z极点为0,41.11j p ±-=实轴上的根轨迹区间： －∞,－1,－1,0 渐进线：分离点：22231+++-=s as s s K解得01=ds dK特征方程022)(1123=++++=K s K as s s s D 令jw s =代入上式：得出与虚轴的交点系统的根轨迹如下图：4-8 根据下列正反馈回路的开环传递函数,绘出其根轨迹的大致形状;1()()1()()12K G s H s s s =++ 2()()1()()12K G s H s s s s =++3()()()12()()13(4)K s G s H s s s s s +=+++解答：1 2 34-15 设单位反馈系统的开环传递函数为确定a 值,使根轨迹图分别具有：0、1、2个分离点,画出这三种情况的根轨迹;解答：首先求出分离点：分离点：321s s K s a +=-+ 解得2122(31)20()dK s a s as ds s a +++=-=+得出分离点1,2d =当119a <<时,上面的方程有一对共轭的复根当911<>a a 或时,上面的方程有两个不等的负实根当119a a ==或时,上面的方程有两个相等的实根1当1=a 时 系统的根轨迹为：可以看出无分离点 ,故排除2当91=a 时 系统的根轨迹为：可以看出系统由一个分离点 3当1>a 时 比如3=a 时系统的根轨迹为：可以看出系统由无分离点 4当91<a 时 比如201=a 时系统的根轨迹为： 可以看出系统由两个分离点 5当191<<a 时 比如21=a 时系统的根轨迹为：可以看出系统由无分离点 第五章 频域分析法5-1设单位反馈控制系统开环传递函4()1G s s =+,当将()sin(260)2cos(45)r t t t =+--作用于闭环系统时,求其稳态输出;解答：开环传递函数14)(+=s s G 闭环传递函数54)(+=Φs s闭环频率特性54)()()(+==Φωωωωαj e M j j当ω=2时,M2=,α2=； 当ω=1时,M1=,α1=； 则闭环系统的稳态输出：5-2 试求110()4G s s =+24()(21)G s s s =+3(1)()(1,)1K s G s K T Ts ττ+=>>+的实频特性()X ω、虚频特性()Y ω、幅频特性()A ω、相频特性()ϕω;解答：⑴4arctan 222216101610164016)4(10410)(wj e w w w j w w jw jw jw G -+=+-+=+-=+=则21640)(w w X +=,21610)(w ww Y +-=⑵)21arctan 180(2331444448)12(4)(wj ew w w w j w w w jw jw jw G ++=+-+-=+=则 w w w w X +-=348)( , w w w Y +-=344)(⑶)]arctan()[arctan(222222222111)(1)1(1)1()(wT w j e w T w k w T w T k j w T Tw k jTw w j k jw G -++=+-+++=++=τττττ则2221)1()(w T Tw k w X ++=τ,221)()(w T wT k w Y +-=τ 5-4 绘制下列传递函数的对数幅频渐近线和相频特性曲线;14()(21)(81)G s s s =++ 2()242()(0.4)(40)s G s s s +=++ 3228(0.1)()(1)(425)s G s s s s s s +=++++ 4210(0.4)()(0.1)s G s s s +=+解答：1转折频率为21,8121==w w2 3 45-10 设单位负反馈系统开环传递函数; 110()(0.51)(0.021)G s s s s =++,21()as G s s +=试确定使相角裕量等于45的α值; 2 3()(0.011)KG s s =+,试确定使相角裕量等于45的K 值;32()(100)KG s s s s =++,,试确定使幅值裕量为20dB 的开环增益K 值;解答：1由题意可得：解得： ⎩⎨⎧==84.019.1αc w2由题意可得：解得： ⎩⎨⎧==83.2100k w c3由题意可得：解得： ⎩⎨⎧==1010k w g5-13 设单位反馈系统开环传递函数 试计算系统的相角裕量和幅值裕量;解答：由18002.0arctan 5.0arctan 90)(-=---=g g g w w w γ所以幅值裕量)(14dB h =故16102.0arctan 5.0arctan 90)(-=---=c c c w w w ϕ所以相角裕量19161180)(=-=c w γ系统的幅频特性曲线的渐近线： 系统的幅相特性曲线：第六章 控制系统的综合与校正6-1 试回答下列问题：1 进行校正的目的是什么为什么不能用改变系统开环增益的办法来实现答：进行校正的目的是达到性能指标;增大系统的开环增益在某些情况下可以改善系统的稳态性能,但是系统的动态性能将变坏,甚至有可能不稳定;2 什么情况下采用串联超前校正它为什么能改善系统的性能答：串联超前校正主要用于系统的稳态性能已符合要求,而动态性能有待改善的场合;串联超前校正是利用校正装置的相位超前特性来增加系统的橡胶稳定裕量,利用校正装置幅频特性曲线的正斜率段来增加系统的穿越频率,从而改善系统的平稳性和快速性;（3）什么情况下采用串联滞后校正它主要能改善系统哪方面的性能答：串联滞后校正主要是用于改善系统的稳态精度的场合,也可以用来提高系统的稳定性,但要以牺牲快速性为代价;滞后校正是利用其在高频段造成的幅值衰减,使系统的相位裕量增加,由于相位裕量的增加,使系统有裕量允许增加开环增益,从而改善稳态精度,同时高频幅值的衰减,使得系统的抗干扰能力得到提高;思考题：1. 串联校正装置为什么一般都安装在误差信号的后面,而不是系统股有部分的后面2. 如果1型系统在校正后希望成为2型系统,但又不影响其稳定性,应采用哪种校正规律6-3 设系统结构如图6-3图所示,其开环传递函数0()(1)KG s s s =+;若要求系统开环截至频率 4.4c ω≥rad/s,相角裕量045γ≥,在单位斜坡函数输入信号作用下,稳态误差0.1ss e ≤,试求无源超前网络参数;解答：1由10.1ss e K =≤可得：10K ≥,取10K =2原系统 3.16c ω= rad/s,017.6γ=,不能满足动态性能指标;3选' 4.4c ω=rad/s,由'0()10lg c L ωα=-即'21020lg10lg cαω=-可得:3.75α=那么0.12T == 无源超前校正网络：10.531()10.121c Ts s G s Ts s α++==++（4） 可以得校正后系统的'51.8γ=,满足性能指标的要求;6-4 设单位反馈系统开环传递函数()()()010.51KG s s s s =++;要求采用串联滞后校正网络,使校正后系统的速度误差系数5(1)v K s =,相角裕量40γ≥;解答： ⑴由00lim ()v s K sG s K→==可得：5K =2 原系统 2.15c ω=,22.2γ=-不满足动态要求3 确定新的'c ω由''1804012(90arctan arctan 0.5)c c ωω-++=---可解得：'0.46c ω=⑷由020lg 20lg (')c b G j ω=-得：0.092b =取'111510cbT ω⎛⎫= ⎪⎝⎭='15c ω得：118T =校正网络为：1111()11181c Tbs s G s Ts s ++=≈++校正后系统的相角裕量'42γ=,故校正后的系统满足性能指标的要求;第七章 非线性控制系统7-1 三个非线性系统的非线性环节一样,线性部分分别为1.2()(0.11)G s s s =+ 2.2()(1)G s s s =+ 3. 2(1.51)()(1)(0.11)s G s s s s +=++ 解答：用描述函数法分析非线性系统时,要求线性部分具有较好的低通滤波性能即是说低频信号容易通过,高频信号不容易通过; 从上图可以看出：系统2的分析准确度高;7-2 一个非线性系统,非线性环节是一个斜率1N -的饱和特性;当不考虑饱和因素时,闭环系统是稳定的;问该系统有没有可能产生自振荡解答：饱和特性的负倒描述函数如下：当1k =时,1()N A -曲线的起点为复平面上的(1,0)j -点; 对于最小相位系统有：闭环系统稳定说明系统的奈氏曲线在实轴(,1)-∞-段没有交点,因此,当存在1k =的饱和特性时,该系统不可能产生自激振荡7-4 判断图中各系统是否稳定,1()N A -与()G j ω的交点是否为自振点;图中P为()G s的右极点个数;解答：首先标出各图的稳定区用阴影部分表示abc da1N-曲线由稳定区穿入不稳定区,交点a是自激振荡点;b1N-曲线由稳定区穿入不稳定区,交点a是自激振荡点;c 交点,a c为自激振荡点,交点b不时自激振荡点;d 闭环系统不稳定;e 交点a不是自激振荡点;f 交点a是自激振荡点7-5 非线性系统如图所示,试确定其自振振幅和频率;题7-5图解答：由题可得下图：由1()()G j N A ω-=得1()()N A G j ω-=即：()()10*412j j j A ωωωπ++=- 320ωω-=得：ω=2403A ωπ-=-得：24020 2.1233A ππω===振幅为203π7-6非线性系统如图所示,试用描述函数法分析当10K =时,系统地稳定性,并求K 的临界稳定值;题7-6图解答：由题可得下图：K 的临界稳定值为：010653K == 所以,当06K <<时,()G j ω曲线不包围1()N A -曲线,系统闭环稳定;第八章 线性离散系统8-1 求函数()x t 的Z 变换;1.()1at x t e -=- 2. ()sin x t t t ω=3. ()sin x t t t ω=4. 2()atx t t e -=解答：1. (1)()1(1)()aT aT aT z e z z X z z z e z z e ----=-=----2.2222(1)sin sin ()()2cos 1(2cos 1)Tz z T d z T X z Tz dz z z T z z T ωωωω-=-=-+-+Z 域微分定理3.22222(cos )cos ()2cos 12cos aT aT aT aT aT aT aTze ze T z ze T X z z e ze T z ze T e ωωωω-----==-+-+复数位移定理4.23(1)()4(1)aT aT aT Tze ze X z ze +=-复数位移定理8-2 已知()X s ,试求对应的()X z ;1.3()(1)(2)s X z s s +=++ 2.2()(1)s X z s s =+3.21()s X z s += 4. 21()(1)s e X z s s --=+解答：1. ()321()12(1)2s X s s s s s +==-++++ 2. 2111()1(1)(1)s X s s s s s s s ===-+++ 3. 22111()s X s s s s +==+4. ()()221111()111s s e X s e s s s s s --⎡⎤⎢⎥⎢⎥⎣⎦-==--+++()1211(1)T T Tzz z X z z z z e z --⎛⎫⎡⎤⎪⎢⎥⎪⎢⎥⎣⎦⎝⎭=--+---()121(1)1(1)1()T T T T z z z e T T e z z e ----⎛⎫⎡⎤⎪⎢⎥ ⎪⎣⎦⎝⎭-+++-+=--负偏移定理8-3 已知()X z ,试求()X nT ;1. ()()()1012zX z z z =--2. ()()()20.80.1z X z z z =--3. ()2(1)1.250.25z z X z z z -=-+解答：1. ()()()1012zX z z z =--=10()21zz z z ---2. ()()()20.80.1z X z z z =--81770.80.1z zz z =---3.()2(1)1.250.25z zX zz z-=-+(1)(0.25)(1)z zz z-=--(0.25)zz=-8-6 已知系统的结构如图所示,1T s=,试求系统的闭环脉冲传递函数()zφ;解答：211111 ()*(1)1(1)TsTseG s es s ss s s--⎛⎫⎪⎪⎝⎭-==--+++思考题：1. 在单位阶跃输入作用下,试求上题所给系统的输出()c t;2. 系统结构如上题,试求当输入为()1()r t t=、t、2t时的稳态误差;。