正式稿二分法求方程的根演示文稿
- 格式:ppt
- 大小:2.60 MB
- 文档页数:21


⽤⼆分法求⽅程的根总时间限制: 1000ms 内存限制: 65536kB题⽬链接:/function1/4/描述⽤⼆分法求下⾯⽅程在(-10, 10)之间的⼀个根。
2x3- 4x2+ 3x- 6 = 0输⼊⼀个⼩于1的⾮负实数e,它的值表⽰所能允许的误差输出⼀个实数,其值为求得的⼀个根,要求精确到⼩数点后8位。
若该区间上没有根,则输出“No Solution”样例输⼊样例输出2.00000000提⽰对于⼀个连续函数f(x),若f(a)*f(b) <= 0,则f(x)在区间[a, b]内⾄少有⼀个根。
特别的,对于⼀个单调的连续函数,上述定理得逆定理也成⽴若[a, b]上有根,则可进⼀步考察根是否在 [a, (a+b)/2]内,或者在[(a+b)/2, b]内。
若b-a <= e 则可终⽌迭代,并认为(a+b)/2是⼀个近似解,将它输出请使⽤double类型!1 #include<stdio.h>2 #include<math.h>3double f(double x);4double fun(double a,double b,double e);5int main()6 {7double e,x1,x2,x;8 x1=-10;x2=10;9 scanf("%lf",&e);10 x=fun(x1,x2,e);11 printf("%.8lf\n",x);12return0;13 }14double f(double x)15 {16double y;17 y=2*x*x*x-4*x*x+3*x-6;18return y;19 }20double fun(double a,double b,double e)21 {22double fa,fb,fc,c;23 fa=f(a);24 fb=f(b);25 c=(a+b)/2;26while(fabs(b-a)>e)27 {28 fc=f(c);29if(fc==0)30 {31break;32 }33else if(fc*fa<0)34 {35 b=c;36 fb=fc;37 }38else39 {40 a=c;41 fa=fc;42 }43 c=(a+b)/2;44 }45return c;46 }这个题⽬要⽤while语句实现才可以通过。

实验7二分法求方程的根实验7 二分法求方程的根一、问题:求324100x x +-=于区间[1,2]内的一个实根,且要求精确到0.001 二、算法:第一步:计算);(),(21b f y a f y ←←第二步:计算)(),(5.0000x f y b a x ←+←,若00ε<="" ,则输出0x="">否则转第三步; 第三步:若010<="" ,则置;,020y="">第四步; 第四步:若1ε>-a b 则转第二步;否则,输出0x 结束.三、练习编写程序或函数实现上以上区间的近似解,要求记录迭代次数。
函数或程序为:结果为:迭代次数为:四、逐步搜索法求方程根的存在区间在给定的区间[,]a b上判定根的大致分布,从区间左端点a出发,按某个预定的步长h一步一步地向右跨,每跨一步进行一次根的搜索,并记录所有的根的存在区间。
用你编写的程序搜索问题中[0,5]的根的存在区间,步长要求为0.1 h函数为:根的存在区间为:五、综合练习(选做)用逐步搜索法找到根的存在区间,并用二分法求出在该区间上方程根的近似解。
附:分组名单星期二下午5-6节第1组组长:陈絮莹缪妃何贵堂刘钰马倩第2组组长:李杰玉黎筱惠雷霞肖娴林碧珍朱元正第3组组长:陈静苏小丽李郑何淑楠田冬秀曾敬军第4组组长:杨欣王雪梅徐莉萍石小芳雷敏唐嘉第5组组长:杨佳悦郭滢李媛媛何可陈思露第6组组长:王钰琪寇玠杨丹熊晨曦周丹第7组组长:姚瑶高倩倩金杨周海宁杨琴第8组组长:雷芳陈艳王玉娇余非张雪王海燕星期三下午5-6节第9组组长:刘超慧王玉利秦佳丽张青梅廖婷程思远第10组组长:杨琴冯康欣黄宜纯田晓东郑美艳第11组组长:黄倩肖雪梅舒玉秀杨阳黄倩宋亚超第12组组长:乔欢曹人月万袁源刘学勤师小诚沈金勇第13组组长:张全兴程德超冯啸魏丹李茜罗凤菊第14组组长:张洋何婷婷刘云丹彭英萍马静第15组组长:杨丽王书琪袁杰宋慧玲杨璐萍李琳玲星期三下午7-8节第16组组长:李欢蒋书丽康斯梦王菊花李芝琴第17组组长:杨梅郑雨来李维刘玉兰羊玲第18组组长:左艳君古月黄文凤杨娟胡洲黄川第19组组长:吴星谭婷张欢向巧钱强陈虹弟第20组组长:曾大超胡敏马树述罗玉婷第21组组长:石章波拉吉石明岳榆川金小刚张泽松第22组组长:贾孙鹏袁鹏颜冬芹陈诚张博第23组组长:李自强黄金辉彭琦岳琪李宾李闯第24组组长:王文媛林小渝刘燕严英何思敏穆芦芸。

【例5.21】二分法求方程的根。
求方程x3+4x2+x+1=0在[-5,5]之间的近似根,误差为10-4。
若函数有实根,则函数的曲线应和x轴有交点,在根附近的左右区间内,函数的值的符号应当相反。
利用这一原理,逐步缩小区间的范围,保持在区间的两个端点处函数值的符号相反,就可以逐步逼近函数的根。
设f (x)在[a, b]上连续,且f (a) f (b)<0, 找使f (x)=0的点。
如图5-7-2所示。
图5-7-2 二分法示意图二分法的步骤如下:①取区间[a, b]中点x=(a+b)/2。
②若f (x)=0, 即(a+b)/2为方程的根。
③否则,若f (x)与f (a)同号,则变区间为[x,b];异号,则变区间为[a,x]。
④重复①~③各步,直到取到近似根为止。
#include "stdio.h"#include "math.h"main(){ float a,b,x;float fa,fb,fx;a=-5;b=5;fa=a*a*a+4*a*a+a+1;fb=b*b*b+4*b*b+b+1;do{ x=(a+b)/2;fx=x*x*x+4*x*x+x+1;if(fa*fx<0){ b=x;fb=b*b*b+4*b*b+b+1;}else{ a=x;fa=a*a*a+4*a*a+a+1;}}while(fabs(fa-fb)>1e-4);printf("x=%f\n",(a+b)/2);printf("f(%f)=%f",(a+b)/2,fa);}运行结果:x=-3.806303f(-3.806303)=-0.000059经过多次迭代,当x= -3.806 303时,f(x)的结果为-0.000 059已经接近0,误差小于10- 4数量级。
读者可进行简单的改写,输出每一次的迭代结果。

二分法求方程的实根一:实验目的 通过编程实现二分法,并利用所编程序求函数x e x y --=3在(0,1)的近似解,然后比较和计算器所求的结果,从理性和实践上认识两种计算方法。
二:基本原理连续函数的零点定理1、假定f(x)在区间(x ,y )上连续 , 先找到a 、b 属于区间(x ,y ),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2]。
2、假设f(a)<0,f(b)>0,a<b①令a a =1,()11121,b a x b b +==,如果f(x)=0,该点就是零点。
如果0)()(1<x f a f ,则新的有根区间为[][]x a b a ,,122=;否则[][]122,,b x b a =。
此时有[][]2211,,b a b a ⊃,且()112221a b a b -=-。
对区间[]22,b a 重复上述做法多步有[][][][] n n b a b a b a b a ,,,,332211⊃⊃⊃且()a b a b n n n -=--121(式1)记*x 为0)(=x f 的根,我们有[]n n b a x ,*∈,即),3,2,1(* =≤≤n b x a n n 由(式1)及夹逼定理有:*lim lim x b a n n n n ==∞→∞→,实际计算时,当ε<-)(n n a b 时,取)(21*n n b a x +≈作为所求根近似值。
三:实验步骤1:建立如下函数文件f.m :Function f=f(x)f=x e x --32:通过如下框图编写二分法程序:erfen.m开始输入f,a,b,delta计算fa,fb,fa*fbfa*fb>0计算最多二分次数max1计算c=(a+b)/2, fcfc=0fb*fc>0b=c,a=a a=c,b=b|a-b|<=0.0005结束是否是否是否是否(3)、在Matlab 命令窗口键入:[c,err,yc]=bisect(‘f ’,0,1,0.005)(4)、得出结果,并与计算器所得结果比较分析误差。

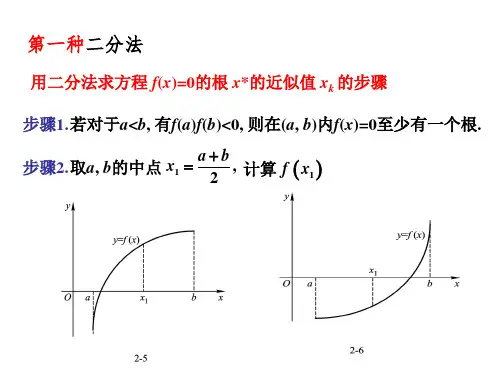


你能说出二分法的意义及用二分法求函数零点近似值的步骤吗?1.二分法的意义对于在区间[,]上连续不断且满足·<0的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).2.给定精确度,用二分法求函数零点近似值的步骤如下:(1)确定区间,,验证·<0,给定精确度;(2)求区间,的中点;(3)计算:1若=,则就是函数的零点;2若·<0,则令=(此时零点);3若·<0,则令=(此时零点);(4)判断是否达到精确度;即若<,则得到零点近似值(或);否则重复步骤2-4.结论: 由函数的零点与相应方程根的关系,我们可用二分法来求方程的近似解.下列给定程序中,函数fun的功能是:应用递归算法求某数a的平方根。
求平方根的迭代公式如下:x1=(1/2)*(x0+a/x0)例如,2的平方根值为1.414214。
#include <stdio.h>#include <math.h>/********found********/double fun(double a, double x0){double x1, y;x1=(x0+ a/x0)/2.0;/********found********/if( fabs(x1-x0)>=0.00001 )y=fun(a,x1);elsey=x1;return y;}main( ){double x;printf("Enter x: ");scanf("%lf",&x);printf("The square root of %lf is %lf\n",x,fun(x,1.0)); }。
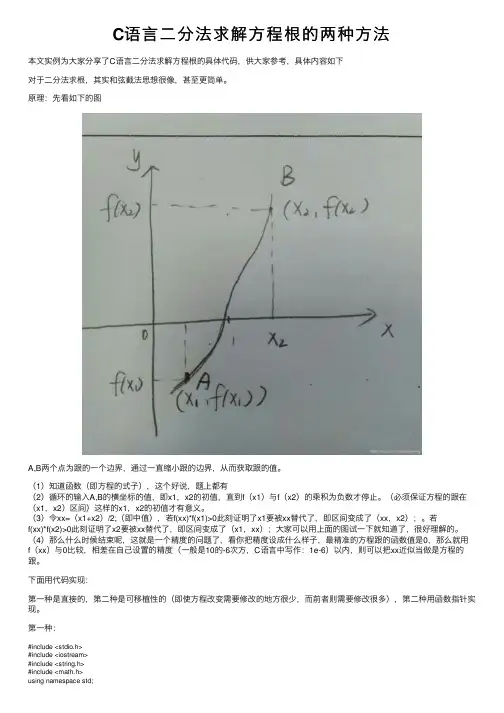
C语⾔⼆分法求解⽅程根的两种⽅法本⽂实例为⼤家分享了C语⾔⼆分法求解⽅程根的具体代码,供⼤家参考,具体内容如下对于⼆分法求根,其实和弦截法思想很像,甚⾄更简单。
原理:先看如下的图A,B两个点为跟的⼀个边界,通过⼀直缩⼩跟的边界,从⽽获取跟的值。
(1)知道函数(即⽅程的式⼦),这个好说,题上都有(2)循环的输⼊A,B的横坐标的值,即x1,x2的初值,直到f(x1)与f(x2)的乘积为负数才停⽌。
(必须保证⽅程的跟在(x1,x2)区间)这样的x1,x2的初值才有意义。
(3)令xx=(x1+x2)/2;(即中值),若f(xx)*f(x1)>0此刻证明了x1要被xx替代了,即区间变成了(xx,x2);。
若f(xx)*f(x2)>0此刻证明了x2要被xx替代了,即区间变成了(x1,xx);⼤家可以⽤上⾯的图试⼀下就知道了,很好理解的。
(4)那么什么时候结束呢,这就是⼀个精度的问题了,看你把精度设成什么样⼦,最精准的⽅程跟的函数值是0,那么就⽤f(xx)与0⽐较,相差在⾃⼰设置的精度(⼀般是10的-6次⽅,C语⾔中写作:1e-6)以内,则可以把xx近似当做是⽅程的跟。
下⾯⽤代码实现:第⼀种是直接的,第⼆种是可移植性的(即使⽅程改变需要修改的地⽅很少,⽽前者则需要修改很多),第⼆种⽤函数指针实现。
第⼀种:#include <stdio.h>#include <iostream>#include <string.h>#include <math.h>using namespace std;double f(double x){return (x*x*x-3*x*x+3*x-1);}int main(){double x1,x2,xx;//x1,x2代表区间左右边界,xx代表⽅程跟的值do{scanf("%lf%lf",&x1,&x2);}while(f(x1)*f(x2)>0);//保证f(x1)和f(x2)是异号,这样才可以进⾏下⼀步的精准区间,否则,重新输⼊x1,x2的值do{xx=(x1+x2)/2;if(f(xx)*f(x1)>0)x1=xx;elsex2=xx;}while(fabs(f(xx))>=1e-7);//le-6代表1*10的-6次⽅,它的值将影响到跟的准确度的问题printf("%.2lf\n",xx);return 0;}第⼆种:#include <stdio.h>#include <iostream>#include <string.h>#include <math.h>using namespace std;double f(double x){return (x*x*x-3*x*x+3*x-1);}double erfen(double x1,double x2,double (*p)(double))//double (*p)(double)为形参,相当于函数别名{double xx;do{xx=(x1+x2)/2;if((*p)(xx)*(*p)(x1)>0)x1=xx;elsex2=xx;}while(fabs((*p)(xx))>=1e-7);//le-7代表1*10的-6次⽅,它的值将影响到跟的准确度的问题return xx;}int main(){double x1,x2;double f(double);double (*p)(double);p=f;do{scanf("%lf%lf",&x1,&x2);}while((*p)(x1)*(*p)(x2)>0);//保证f(x1)和f(x2)是异号,这样才可以进⾏下⼀步的精准区间,否则,重新输⼊x1,x2的值 printf("%.2lf\n",erfen(x1,x2,f));return 0;}以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。