当前位置：文档之家 › 二分法求解方程 人教课标版

二分法求解方程 人教课标版

  • 格式：ppt
  • 大小：1.36 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

人教版新课标高中数学精品系列 必修一3.1.2用二分法求方程的近似解 课件(四课时)

人教版新课标高中数学精品系列 必修一3.1.2用二分法求方程的近似解 课件(四课时)


2 3x 7
x
的近似解（精确到0.1）。
例2．求函数
y x 2x x 2
3 2
的零点，并画出它的图象。
例3．已知函数 f ( x) ax bx 的图象如图所示，则 A．b (,0) B． b (0,1) b (2, ) D． C． b (1, 2)
，那么函数 y f ( x) 在区间 [ a, b] 内至少有一个实数
根、若能证明 y f ( x) 在 [a, b] 上的单调性，则在
[a, b] 有且只有一个零点、再在其它区间内同理去寻找。
解二：试探着找到两个x对应值为一正一负（至少 有一个）；再证单调增函数即可得有且只有一个。
解三：构造两个易画函数，画图，看图象交点 个数，很实用。
3．计算 f (c) ： （1）若 f (c) =0，则c就是函数的零点，计算终止； （2）若 f (a) f (c) 0 ，则令b=c（此时零点 x0 a, c ）；
（3）若 f (c) f (b) 0 则令a=c（此时零点
x0 c, b 。(用列表更清楚)
ab 的中点 c 2
3
2
cx d
2 1
2 f ( x ) mx (m 3) x 1 例4．已知函数 的图象与 x 轴的交点至少有一个在原点右侧，则实数
m 的取值范围是（ ）
A．(0,1] C． (,1) B．
(0,1)
D．
(,1]
3.1.2 用二分法求方程的近似解 (2)
问题1 在一个风雨交加的夜里，从某水库闸房
到防洪指挥部的电话线路发生了故障，这上一 条10km长的线路，如何迅速查出故障所在？
方法分析：
3.1.2用二分法求方程的近似解教案【人教版】高中数学必修

3.1.2用二分法求方程的近似解教案【人教版】高中数学必修

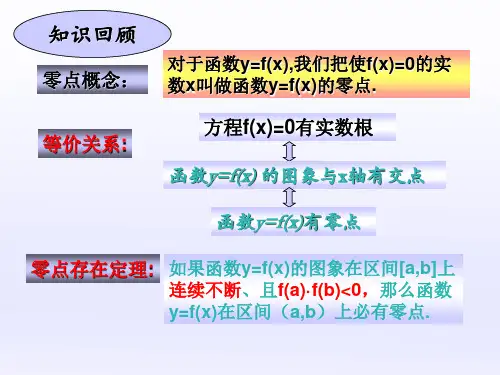
用二分法求方程的近似解教学目标知识与技能通过具体实例理解二分法的概念及其适用条件，了解二分法是求方程近似解的常用方法，从中体会函数与方程之间的联系及其在实际问题中的应用．过程与方法能借助计算器用二分法求方程的近似解，并了解这一数学思想，为学习算法做准备．情感、态度、价值观体会数学逼近过程，感受精确与近似的相对统教学重点通过用二分法求方程的近似解，体会函数的零点与方程根之间的联系，初步形成用函数观点处理问题的意识．教学难点恰当地使用信息技术工具，利用二分法求给定精确度的方程的近似解．教学方法动手操作、分组讨论、合作交流、课后实践教学过程例：求函数()6xxf的零点（即的根）2ln-+=x对于为一次或二次函数，我们有熟知的公式解法（二次时，称为求根公式）．一般的五次以上代数方程的根式解不存在求根公式，因此对于高次多项式函数及其它的一些函数，有必要寻求其零点的近似解的方法我们已经知道，函数()6xf在区间（2，3）内有零点，进一x=xln-+2步的问题是，如何找出这个零点？师：一个直观的想法是:如果能够将零点所在的范围尽量缩小，那么在一定精确度的要求下，我们可以得到零点的近似值.为了方便，下面我们通过“取中点”的方法逐步缩小零点所在的范围.师：引导学生分析理解求区间，的中点的方法．做一做第一步：取区间(2，3)的中点2.5，用计算器算得f(2.5)≈－0.084.因为f(2.5)·f(3)＜0，所以零点在区间(2.5，3)内.第二步：取区间(2.5，3)的中点2.75，用计算器算得f(2.75)≈0.512. 因为f(2.5)·f(2.75)＜0，所以零点在区间(2.5，2.75)内.结论:由于(2，3) (2.5，3) (2.5，2.75)，所以零点所在的范围确实越来越小了.如果重复上述步骤，那么零点所在的范围会越来越小师：这样，在一定精确度下，我们可以在有限次重复相同步骤后，将所得的零点所在区间内的任意一点作为函数零点的近似值，特别地，可以将区间端点作为零点的近似值.例如，当精确度为0.01时，由于|2.5390625－2.53125|=0.0078125＜0.01，所以，我们可以将=2.53125作为函数零点的近似值，也即方程根的近似值.探索发现议一议：你能说出二分法的意义及用二分法求函数零点近似值的步骤吗？1.二分法的意义对于在区间[a，b]上连续不断且满足f(a)·f(b)＜0的函数y=f(x)，通过不断地把函数的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法(bisection)．2.给定精确度ε，用二分法求函数零点近似值的步骤如下：(1)确定区间[]b a,，验证f(a)·f(b)＜0，给定精确度ε；(2)求区间(a,b)的中点c；(3)计算：f(c)1若f(c)=0，则c就是函数的零点；2若f(a)·f(c)＜0，则令b=c（此时零点()c ax,∈）；3若f(c)·f(b)·＜0，则令a=c（此时零点()b cx,∈）；(4)判断是否达到精确度ε；即若＜，则得到零点近似值a（或b）；否则重复步骤2-4．结论: 由函数的零点与相应方程根的关系，我们可用二分法来求方程的近似解.例2：用二分法求方程732=+xx的近似解（精确度0.1）练习：1，求方程23x+3x-3=0的一个实数解，精确到0.012，探求2x-x2=0的近似解1.方程4223=-+-gxxx在区间[]4,2-上的根必定属于区间（）A.)1,2(- B.)4,25(C.)4,1(πD.)25,47(A.函数)(xf在区间[]1,0内有零点 B.函数)(x f在区间[]2,1内有零点C.函数)(xf在区间[]2,0内有零点 D.函数)(x f在区间[]4,0内有零点3.函数xy=与1+=xy图象交点横坐标的大致区间为（）A.)0,1(- B.)1,0( C.)2,1( D.)3,2(4.下图4个函数的图象的零点不能用二分法求近似值的是5.写出两个至少含有方程01223=--+x x x 一个根的单位长度为1的区间或。

4.5.2用二分法求方程的近似解课件(人教版)

4.5.2用二分法求方程的近似解课件(人教版)


B．3，4
• C．5，4
D．4，3
• 解析
图象与x轴有4个交点，所以零点的个数为4；左右函数值异号的零点有
3个，所以可以用二分法求解的个数为3，故选D.
• (2)(多选)下列函数中，能用二分法求函数零点的有 ACD
• A．f(x)＝3x－1
B．f(x)＝x 2 －2x＋1
• C．f(x)＝4x
D．f(x)＝e x －2
• 解析
f(x)＝x 2 －2x＋1＝(x－1) 2 ，f(1)＝0，当x<1时，f(x)>0；当
x>1时，f(x)>0，在零点两侧函数值同号，不能用二分法求零点，
其余选项中函数的零点两侧的函数值异号．故选A、C、D.
•
|通性通法|
•
•
二分法的适用条件
判断一个函数能否用二分法求其零点的根据是：其图象在零
中点的值
2.5
2.75
2.625
2.5625
2.53125
2.546875
2.5390625
2.53515625
中点函数近似值
–0.084
0.512
0.215
0.066
–0.009
0.029
0.010
0.001
当精确度为0.01时，由于|2.5390625-2.53125| =0.007 812 5＜0.01，所以，
如何求得一般方程的根呢？
二、探究新知
视察图形，怎样求方程lnx+2x-6=0的根？
1．二分法：
对于区间[a，b]上连续不断且f(a)·f(b)＜0的函数y=f(x)，
通过不断地把函数f(x)的零点所在的区间一分为二，使
3.1.2用二分法求方程的近似解课件人教新课标

3.1.2用二分法求方程的近似解课件人教新课标


方法点评 用二分法求方程 f(x)=0（或g(x)=h(x)）近似解的基本 步骤: 1.寻找解所在区间 （1）图象法 先画出y = f(x)图象，视察图象与x轴的交点横坐标所 处的范围；
或画出y=g(x)和y=h(x)的图象,视察两图象的交点横坐 标的范围. （2）函数法 把方程均转换为 f(x)=0的情势，再利用函数y=f(x) 的有关性质（如单调性）来判断解所在的区间.
2.y=f(x)满足f(a)f(b)<0，则在(a,b)内必有零点.
思考：对下列图象中的函数，能否用二分法求函数零
点的近似值？为什么？ y y
o
x
o x
不行,因为不满足 f(a)*f(b)<0
1.二分法的原理 2.二分法的应用：求方程近似解
世间没有一种具有真正价值的东西，可以 不经过艰苦辛勤的劳动而得到。
列出下表：
根所在区间
区间端点函数值符号 中点值 中点函数值符号
（2，3）
f(2)<0,f(3)>0
2.5
f(2.5)<0
（2.5，3） （2.5，2.75）
f(2.5)<0，f(3)>0 2.75 f(2.5)<0，f(2.75)>0 2.625
f(2.75)>0 f(2.625)>0
（2.5，2.625）
x 0 1 23 4 5 6 7
8
f(x) -6 -2 3 10 21 40 75 142 273
因为f(1)·f(2)<0所以 f(x)= 2x+3x-7在（1，2）内
有零点x0,取（1，2）的中点x1=1.5，f(1.5)≈ 0.33，
因为f(1)·f(1.5)<0 所以x0 ∈（1，1.5） 取（1，1.5）的中点x2=1.25 ,f(1.25)= -0.87，因
§..用二分法求方程的近似解教案人教版

§..用二分法求方程的近似解教案人教版

§..用二分法求方程的近似解教案人教版
科目
授课时间节次
--年—月—日（星期——）第—节
指导教师
授课班级、授课课时
授课题目
（包括教材及章节名称）
§..用二分法求方程的近似解教案人教版
教材分析
本节课的教学内容是“用二分法求方程的近似解”。该内容是高中数学人教版必修四第四章“不等式”中的一个重要知识点。在此之前，学生已经学习了函数、方程和不等式的基础知识，通过这些知识的学习，学生已经掌握了函数的性质、解方程的方法等。
-反馈作业情况：及时批改作业，给予学生反馈和指导。
学生活动：
-完成作业：认真完成老师布置的课后作业，巩固学习效果。
-拓展学习：利用老师提供的拓展资源，进行进一步的学习和思考。
-反思总结：对自己的学习过程和成果进行反思和总结，提出改进建议。
教学方法/手段/资源：
-自主学习法：引导学生自主完成作业和拓展学习。
- "The history and applications of the bisection method"：这篇文章详细介绍了二分法的历史背景及其在各个领域的应用，有助于学生更好地理解二分法的地位和作用。
在线资源：
- GeoGebra：这是一个免费的数学软件，学生可以通过它来绘制函数图像，实践二分法求解方程的近似解。
d.案例研究环节：提供几个不同类型的方程，让学生运用二分法进行求解，并分析解题过程中的关键步骤。
e.项目导向学习环节：让学生分组选择一个方程，运用二分法编写程序求解，并展示解题过程和结果。
3.确定教学媒体和资源的使用：为了支持教学活动和提高学生的学习效果，将使用以下教学媒体和资源：
a. PPT：制作精美的PPT，用于展示二分法的原理、步骤和实例，提供直观的学习材料。
4.5.2 用二分法求方程的近似解课件(人教版)

4.5.2 用二分法求方程的近似解课件(人教版)


(3)计算 f(c)，并进一步确定零点所在的区间：
①若 f(c)＝0(此时 x0＝c)，则 c 就是函数的零点； ②若 f(a)f(c)＜0(此时 x0∈(a，c))，则令 b＝c；
③若 f(c)f(b)＜0(此时 x0∈(c，b))，则令 a＝c. (4)判断是否达到精确度 ε：若|a－b|＜ε，则得到零点近似值 a(或 b)；
端点(中点)
x0＝－12－2＝－1.5 x1＝－1.25－2＝－1.75 x2＝－1.275－2＝－1.875
端点或中点的函数值 f(－1)>0，f(－2)<0
f(x0)＝4.375>0
18
取值区间 (－2，－1) (－2，－1.5)
f(x1)≈2.203>0
(－2，－1.75)
f(x2)≈0.736>0
(－1.937 5，－ 1.906 25)
(－1.937 5，－ 1.921 875)
20
x6＝－1.937
5－1.921 2
875＝
－1.929 687 5
f(x6)≈0.010 5>0
(－1.937 5，－ 1.929 687 5)
由于|－1.929 687 5＋1.937 5|＝0.007 812 5<0.01，所以函数的一个
2．并非所有函数都可以用二分法求其零点，只有满足： (1)在区间[a，b]上连续不断； (2)f(a)·f(b)<0， 上述两条的函数方可采用二分法求得零点的近似值．
28
当堂达标 固双基
29
1．思考辨析
[答案]
(1)二分法所求出的方程的解都是近似解．( ) (1)× (2)×
(2)函数 f(x)＝|x|可以用二分法求零点．( )
数学必修Ⅰ人教新课标A版3-1-2用二分法求方程的近似解课件(24张)

数学必修Ⅰ人教新课标A版3-1-2用二分法求方程的近似解课件(24张)


数学 必修1
第三章 函数的应用
学案·新知自解
教案·课堂探究
练案·学业达标
第三步：计算 f(c)． (1)若 f(c)＝0，则 c 就是函数的零点； (2)若 f(a)·f(c)<0， 则令 b＝c(此时零点 x0∈(a，c))； (3)若 f(c)·f(b)<0， 则令 a＝c(此时零点 x0∈(c，b))． 第四步：判断是否达到精确度 ε：即若|a－b|<ε，则得到零点近似值 a(或 b)， 否则重复第二步至第四步．
数学 必修1
第三章 函数的应用
学案·新知自解
教案·课堂探究
练案·学业达标
3.1.2 用二分法求方程的近似解
数学 必修1
第三章 函数的应用
学案·新知自解
教案·课堂探究
练案·学业达标
学案·新知自解
数学 必修1
第三章 函数的应用
学案·1．会用二分法求方程的近似解．(重点) 2．明确精确度 ε 与近似值的区别．(易混点) 3．会判断函数零点所在的区间．(难点)
学案·新知自解
教案·课堂探究
练案·学业达标
解析： 利用二分法求函数零点必须满足零点两侧函数值异号．在 B 中， 不满足 f(a)·f(b)<0，不能用二分法求零点，由于 A、C、D 中零点两侧函数值异 号，故可采用二分法求零点．
答案： B
数学 必修1
第三章 函数的应用
学案·新知自解
教案·课堂探究
练案·学业达标
答案： 1.562 5
数学 必修1
第三章 函数的应用
学案·新知自解
教案·课堂探究
练案·学业达标
教案·课堂探究
数学 必修1
是(
第三章 函数的应用
2024春新教材高中数学4.5.2用二分法求方程的近似解教学设计新人教A版必修第一册

2024春新教材高中数学4.5.2用二分法求方程的近似解教学设计新人教A版必修第一册

鼓励学生分享学习“用二分法求方程的近似解”的心得和体会，增进师生之间的情感交流。
（六）课堂小结（预计用时：2分钟）
简要回顾本节课学习的“用二分法求方程的近似解”内容，强调重点和难点。
肯定学生的表现，鼓励他们继续努力。
布置作业：
根据本节课学习的“用二分法求方程的近似解”内容，布置适量的课后作业，巩固学习效果。
九．课后作业
1. 请用二分法求解方程f(x) = x^2 - 4 = 0的近似解，精度要求为0.01。
2. 请用二分法求解方程f(x) = sin(x) = 0的近似解，精度要求为0.01。
3. 请用二分法求解方程f(x) = x^3 - 3x - 1 = 0的近似解，精度要求为0.01。
4. 请用二分法求解方程f(x) = e^x - 1 = 0的近似解，精度要求为0.01。
再次，我在教学中使用了一些教学媒体和资源，如PPT、视频和在线工具等，以提高教学效果。这些教学媒体和资源的使用，使学生能够更直观地了解二分法的应用过程，提高他们的学习兴趣和学习动力。
最后，我在教学中注重培养学生的数据分析、数学建模等能力，通过实际例子的分析和操作，使学生能够将理论知识应用到实际问题中。同时，我也加强对学生的个别辅导，关注他们的学习进度，及时解答他们在学习过程中遇到的困惑。
提醒学生注意作业要求和时间安排，确保作业质量。
六、知识点梳理
本节课的主要教学内容是高中数学4.5.2节中的“用二分法求方程的近似解”。具体内容包括：
1. 二分法的概念及其原理
- 二分法的定义：二分法是一种求解方程近似解的迭代方法，通过不断将方程的解的范围缩小，最终得到方程的近似解。
- 二分法的原理：二分法基于函数的连续性和介值定理，通过判断函数在区间两端取值的正负性，不断将解的范围缩小，直至满足精度要求。
高中数学人教版必修一《第三章3.1.2用二分法求方程的近似解》课件

高中数学人教版必修一《第三章3.1.2用二分法求方程的近似解》课件


2＋4 f(2)·f(4)<0，取区间(2,4)的中点 x1＝ 2 ＝3，计算得 f(2)·f(x1)<0，则此
时零点 x0 所在的区间是( B )
A.(2,4) C.(3,4)
B.(2,3) D.无法确定
答案
1.二分就是平均分成两部分.二分法就是通过不断地将所选区间一分为二， 使区间的两个端点逐渐靠近零点，直至找到零点邻近足够小的区间，根 据所要求的精确度，用此区间的某个数值近似地表示真正的零点. 2.二分法求方程近似解的适用范畴：在包含方程解的一个区间上，函数 图象是连续的，且两端点函数值异号.
答案 ①取区间(2,3)的中点2.5. ②运算f(2.5)的值，用运算器算得f(2.5)≈－0.084.由于f(2.5)·f(3)<0，所 以零点在区间(2.5,3)内.
二分法的概念：
对于在区间[a，b]上连续不断且 f(a)·f(b)<0 的 函 数 y ＝ f(x) ， 通 过 不
断地把函数f(x)的零点所在的区间 一分为二
3.1.2
用二分法求方 程的近似解
数学人教版 高中数学
1.理解二分法的原理及其适用条件； 2.掌控二分法的实行步骤； 3.体会二分法中包蕴的逐渐靠近与程序节课，我们已经知道f(x)＝ln x＋2x－6的零点在区间(2,3)内， 如何缩小零点所在区间(2,3)的范畴？
a＋b (a，b)上有一个零点 x0，且 f(a)f(b)<0，用二分法求 x0 时，当 f( 2 )＝0
时，则函数 f(x)的零点是( B )
A.(a，b)外的点
a＋b B.x＝ 2
a＋b a＋b C.区间(a， 2 )或( 2 ，b)内的任意一个实数
D.x＝a 或 b
4.5.2用二分法求方程的近似解课件(人教版)

4.5.2用二分法求方程的近似解课件(人教版)

(2)用二分法求函数零点近似值的步骤.
）
答案：×，×，×.
辨析2：用二分法研究函数() = 3 + 3 − 1的零点时，第一次经计算(0) <
0，(0.5) > 0，可得其中一个零点0 ∈________，第二次计算________，以上横线
上应填的内容为（ ）.
A.(0，0.5)，(0.25)
B.(0，1)，(0.25)
2.5390625
0.010
(2.53125,2.5390625) 2.53515625
0.001
新知探索
零点所在区间
中点的值
中点函数近似
值
(2,3)
2.5
−0.084
(2.5,3)
2.75
0.512
(2.5,2.75)
2.625
0.215
(2.5,2.625)
2.5625
0.066
(2.5,2.5625)
0，所以0 ∈ (1,1.5).
再取区间(1,1.5)的中点2 = 1.25，用信息技术算得(1.25) ≈ −0.87.因为
(1.25)(1.5) < 0，所以0 ∈ (1.25,1.5).
同理可得，0 ∈ (1.375,1.5)，0 ∈ (1.375,1.4375).
由于|1.375 − 1.4375| = 0.0625 < 0.1，所以，原方程的近似解可取为1.375.
间中点的方法，逐步缩小零点所在的范围.
新知探索
取(2,3)的中点2.5，用计算工具算得(2.5) ≈ −0.084.因为(2.5)(3) < 0，所以零
点在区间(2.5,3)内.
再取区间(2.5,3)的中点2.75，用计算工具算得(2.75) ≈ 0.512.因为(2.5)(2.75) <
用二分法求方程的近似解人教课标版课件

用二分法求方程的近似解人教课标版课件


区间长度 1
0.5 0.25 0.125
概念拓展 实践探究
题11.下列函数的图像中，其中不能用二分法求解其零点的
是（ C ）
y
y
y
y
0
x
0
x
0
x
0
x
A
B
c
D
题2 根据下表，用二分法求函数f(x)＝x3－3x＋1在区间(1,2)上的零点的 近似值(精确度0.1)是___1_._5___.
f(1)＝－1
这能为你提供求函数 零点近似值的思路吗
思路：用区间两个端点的中点， 将区间一分为二……
新知探究 你有进一步缩小函数零点的范围的方法吗？
f (x) ln x 2x 6
2.5
2
2.625 2.75
3
概念形成
二分法的定义：
对于在区间a,b上连续不断且f (a) f (b) 0的函数
y f (x), 通过不断的把函数f (x)的零点所在区间
一分为二，使区间的两个端点逐步逼近零点
，进而得到零点近似值的方法叫做二分法.
给定精确度 0.1，求f x ln x 2x 6零点在2，3
近似值. 初始区间（2，3）且 f (2) 0, f (3) 0
次数
ab
2
1
2.5
f (a b) 2
-0.084
取a
取b
(22.5.5,3 3)
区间长度：
如果沿着线路一小段一小段查找，困难 很多。每查一个点要爬一次电线杆子， 10km长，大约有200根电线杆子。
想一
想 维修线站和医院的所在处分别为点A、B（间距10km)
A
(供电站)
C ED

人教版数学2 用二分法求方程的近似解 配套教学(共19张PPT)教育课件

用二分法求方程的近似解
教学过程：
一、提出问题： 1.能否求解以下几个方程 (1) 2x=4-x (2) x2-2x-1=0 (3) x3+3x-1=0
2.能否求出它们的近似解？
3.什么方法？
y=2x
y
4
1 0 12
y=4-x
x
4
4.能否找到其它的方法，使解更精确？
探究解法
（1）不解方程，如何求方程x2-2x-1=0 的一个正的近似解（精确到0.1）?
四、归纳总结
2、不断二分解所在的区间
若 x 1 (a ,b )不 , f(a 妨 ) 0 ,f(b 设 ) 0
（1）若
f (ab) 0，由
2
f (a) 0，则
x1
(a,
ab) 2
（2）若
f (ab) 0 ，由
2
f
(b)
0，则
x1
(ab,b) 2
（3）若 f (ab) 0，则
2
x1
a
2
b
对(1)、(2)两种情形再继续二分解所在的区间.
四、归纳总结
3、根据精确度得出近似解
当 x1(m,n)，且m, n根据精确度得到的近似值均为同
一个值P时，则x1≈P ，即求得近似解。
练习：
求方程x3+3x-1=0的一个近似解。(精确到0.1) 画y=x3+3x-1的图象比较困难， 变形为x3=1-3x，画两个函数的图象如何？
解：令f(x)=x3+3x-1, 有f(0)<0,f(1)>0,则方程的解在 0,1之间。
(2.53125,2.5390625)
负正
四、归纳总结
用二分法求方程 f(x)=0（或g(x)=h(x)）近似解的基本步骤:

人教课标版(B版)高中数学必修1《二分法》教学课件1


如果函数图象通过零点时穿过了x轴， 则称这样的零点为变号零点，如果没有穿过 x轴，则称这样的零点为不变号零点。
依据这个性质，下面我们介绍求函数零点
的近似值的一种计算方法：二分法。
已知函数y=f(x)定义在区间D上，求它在 D上的一个零点x0的近似值x，使它满足给定 的精确度。
下面我们分步写出用二分法求函数零点
（2）如果f(a0)·f(x0)<0，则零点位于区间[a0， x0]中，令a1=a0，b1=x0；
（3）如果f(a0)·f(x0)>0，则零点位于区间[x0， b0]中，令a1=x0，b1=b0；
第三步：取区间[a1，b1]的中点，则此中点对应
的坐标为
x1
a1
1 2
(b1
a1)
1 2
(a1
b1)
计算f(x1)和f(a1)，并判断：
函数y=f(x)有零点
（2）如何求零点个数及所在区间？
解一：利用计算器或计算机作 x, f (x)的对应
值表，若在区间 (a, b)上连续，并且有 f (a) f (b) 0
那么函数 y f (x)在区间[a, b]内至少有一个实数
根，若能证明 y f (x)在 [a,b]上的单调性，则在
[a,b] 有且只有一个零点.
解二：试探着找到两个x对应值为一正一负 （至少有一个）；再证单调增函数即可得有 且只有一个.
解三：构造两个易画函数，画图，看图象 交点个数，很实用.
（3）连续函数在某个区间上存在零点的判别 方法：
如果函数y=f(x)在区间[a,b]上的图象是连续 不断的一条曲线，并且有f(a)·f(b)<0，那么，函 数y=f(x)在区间(a,b)内有零点.即存在c∈(a,b)， 使得f(c )=0，这个c也就是方程f(x)=0的根.

数学新课标人教A版必修1教学课件：3.1.2 用二分法求方程的近似解


1．二分法的定义 对 于在区间[a，b]上连___续__不__断_且_f_(a_)_·_f_(_b_)<_0_的 函数y＝f(x)，通过不断地把函数f(x)的零点所 在的区间_一__分__为__二__，使区间的两个端点逐步 逼近_零__点__进 而得到零点的近似值的方法，叫 做二分法．由函数的零点与相应方程根的关
必修1 第三章 函数的应用
栏目导引
解析： 由题意知选C. 答案： C
必修1 第三章 函数的应用
栏目导引
2．若函数据如下：
f(1)＝－2
f(1.375)＝－ 0.260
f(1.5)＝0.625
f(1.437 5)＝ 0.162
f(1.25)＝－ 0.984
f(1.406 25)＝－ 0.054
那么方程x3＋x2－2x－2＝0的一个近似根(精确
到0.1)为 ( )
A．1.5
B．1.4
C．1.3
D．1.2
必修1 第三章 函数的应用
栏目导引
解析： ∵|1.437 5－1.375|＝0.062 5＜0.1 ∴f(x)的零点近似值可取1.437 5≈1.4或 1.375≈1.4. 答案： B
栏目导引
要求方程2x3＋3x－3＝0的正实根，可转化为 用二分法求函数f(x)＝2x3＋3x－3的正的零点，
故首先要选定初始区间[a，b]，满足 f(a)·f(b)<0，然后逐步逼近.
必修1 第三章 函数的应用
栏目导引
[解题过程] 令f(x)＝2x3＋3x－3， 经计算，f(0)＝－3<0，f(1)＝2>0，f(0)·f(1)<0， 所以函数f(x)在(0,1)内存在零点， 即方程2x3＋3x＝3在(0,1)内有解． 取(0,1)的中点0.5，经计算f(0.5)<0，又f(1)>0， 所以方程2x3＋3x－3＝0在(0.5,1)内有解． 如此继续下去，得到方程的正实数根所在的区
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
输入ε；
输出 a b . 2
a:=-1; b:=5;
赋值语句
条件语句
If
f (a b） 0 2
then 跳出repeat 循环; else if f(a) f (a b） 0
2
then b:= a b
2
else a:=
பைடு நூலகம்
ab 2
循环语句
repeat If f (a b） 0
算法：
简单地说，算法是完成某项 工作的方法和步骤。
现代意义上的“算法”通常 是指可以用计算机来解决的 某一类问题的程序或步骤。 例如二分法
算法的基本结构
顺序结构 条件结构 循环结构
顺序结构
选择结构
循环结构
顺序结构的算法
尺规作图，确定线段 AB的一个5等分点．
顺序结构的特点： 算法按照书写顺序执 行
四、用基本语句表达求解步骤
输入ε； a:=-1;
b:=5; repeat If f (a b） 0
2
then 跳出repeat 循环;
else if f(a)f(a b） 0
2
then b:=
ab 2
else a:= a b
2
until b-a < ε;
ab
输出 2
.
输入、输出语句
实例分析 二分法求解方程
问题
我们知道，对[-1,5]上的函数y=f(x),若 f(-1)·f(5)<0,则存在ξ∈ [-1,5]，使f(ξ)=0.
如何求出方程f(x)=0的近似解呢？ 即如何求出c ∈ [-1,5]，使|c-ξ|<0.001?
一、算理
先取[-1,5]的中点2,判断f(2)的值是否为0，若f(2)=0，那么2就是方 程的解；若f(2)≠0， 那么区间[-1，2]、[2，5]中必有一个是方程 的可解区间。
2
then 跳出repeat 循环; else if f(a) f (a b） 0
2
then b:= a b
2
else a:=
ab 2
until b-a < ε;
说明
选择一个适当的语言实现上述步骤， 标准并未对这一点进行要求。
有条件的地方可用计算机实现
算法
什么是算法:基本思想 算法的基本结构 算法的基本特点 算法的描述 算法学习的意义 算法教学中要注意的问题
如此反复进行下去，直到可解区间的长度满足要求的精度或者区间中点 的函数值为0。
二、自然语言表达求解步骤
第一步，确定有解区间[a,b] 第二步，取[a,b]的中点 第三步，计算函数在中点处的函数值 第四步，判断中点处函数值是否为0 第五步，判断新的有解区间的长度是否
小于ε
三、框图语言表达求解步骤
若f(2)·f(5)<0,那么在[2，5]内有方程y=f(x)的解，称[2，5]为可解区间。 若f(-1)·f(2)<0,那么在[-1，2]内有方程y=f(x)的解，称[-1，2]为可解区间。
问题：可解区间的长度是否小于精度？ 如何缩小可解区间？
再取其中可解区间，比如[2,5]的中点3.5，判断f(3.5)的值是否为0 判断可解区间 将可解区间的长度与要求的精度进行比较 缩小可解区间，再看是否满足要求的精度
算法思想 是贯穿高中课程的基本思想
算法思想
代数中 方程求解 不等式求解 几何中 点到直线的距离 异面直线的距离 统计中
算法教学中要注意的问题
注重算法的基本思想的理解 算法教学必须通过实例进行 算法教学要注意循序渐进，先具体再抽
象，先了解算理，再描述算法
同学们，再见！
选择结构的算法
求三个数中的最大数 选择结构的 特点
算法中需要进行判断， 判断的结果决定后面 的步骤。
循环结构的算法
输出1000以内所有能被 3和5整除的正整数。
循环结构的三个要素 1）循环变量 2）循环体 3）循环终止条件
循环结构的算法
循环结构比较困难的是，决定循环结束 的条件，我们通常都是用变量表示循环 结束的条件，一般有两种情况：
一是，用循环变量表示循环的次数； 二是，用循环变量表示精度或其他的量。
算法的特点
有穷性 确定性 可行性
算法的描述
一般有下列三种描述方法 1）自然语言 2）框图语言——流程图 3）程序语言
基本语句
输入输出语句 赋值语句 条件语句 循环语句
算法学习的意义
有利于培养学生的思维能力 有利于培养学生理性精神和实践能力 有利于学生理解构造性数学