大学物理磁场作业(二)习题与解答

衡水学院 理工科专业 《大学物理B 》 稳恒磁场 习题解答一、填空题（每空1分）1、电流密度矢量的定义式为：dIj n dS ⊥=，单位是：安培每平方米（A/m 2） 。

2、真空中有一载有稳恒电流I 的细线圈，则通过包围该线圈的封闭曲面S 的磁通量Φ = 0 ．若通过S 面上某面元d S 的元磁通为d Φ，而线圈中的电流增加为2I 时,通过同一面元的元磁通为d Φ＇，则d Φ∶d Φ＇= 1:2 。

3、一弯曲的载流导线在同一平面内，形状如图1(O 点是半径为R 1和R 2的两个半圆弧的共同圆心，电流自无穷远来到无穷远去)，则O 点磁感强度的大小是2020100444R IR IR IB πμμμ-+=。

4小为πR 2c Wb。

5、如图2所示通有电流I 的两根长直导线旁绕有三种环路；在每种情况下，等于：对环路a ：dB l ⋅⎰=____μ0I __； 对环路b ：d B l ⋅⎰=___0____； 对环路c ：d B l ⋅⎰ =__2μ0I __。

6、两个带电粒子，以相同的速度垂直磁感线飞入匀强磁场，它们的质量之比是1∶4，电荷之比是1∶2，它们所受的磁场力之比是___1∶2__，运动轨迹半径之比是_____1∶2_____。

二、单项选择题（每小题2分）（ B ）1、均匀磁场的磁感强度B 垂直于半径为r 的圆面．今以该圆周为边线，作一半球面S ，则通过S 面的磁通量的大小为A. 2πr 2BB. πr 2BC. 0D. 无法确定的量（ C ）2、有一个圆形回路1及一个正方形回路2，圆直径和正方形的边长相等，二者中通有大小相等的电流，它们在各自中心产生的磁感强度的大小之比B 1 / B 2为A. 0.90B. 1.00C. 1.11D. 1.22（ D ）3、如图3所示，电流从a 点分两路通过对称的圆环形分路，汇合于b 点．若ca 、bd 都沿环的径向，则在环形分路的环心处的磁感强度A. 方向垂直环形分路所在平面且指向纸内B. 方向垂直环形分路所在平面且指向纸外C ．方向在环形分路所在平面内，且指向aD ．为零（ D ）（ C ）绕AC 轴旋转时，在中心O 点产生的磁感强度大小为B 1；此正方形同样以角速度绕过O 点垂直于正方形平面的轴旋转时，在O 点产生的磁感强度的大小为B 2，则B 1与B 2间的关系为A. B 1 = B 2B. B 1 = 2B 2 C ．B 1 = 21B 2 D ．B 1 = B 2 /4（ B ）6、有一半径为R 的单匝圆线圈，通以电流I ，若将该导线弯成匝数N = 2的平面圆线圈，导线长度不变，并通以同样的电流，则线圈中心的磁感强度和线圈的磁矩分别是原来的 (A) 4倍和1/8． (B) 4倍和1/2． (C) 2倍和1/4． (D) 2倍和1/2． 三、判断题（每小题1分，请在括号里打上√或×）（ × ）1、电源的电动势是将负电荷从电源的负极通过电源内部移到电源正极时，非静电力作的功。

磁场典型例题（一）磁通量的大小比较与磁通量的变化例题1. 如图所示，a、b为两同心圆线圈，且线圈平面均垂直于条形磁铁，a的半径大于b，两线圈中的磁通量较大的是线圈___________。

解析：b 部分学生由于对所有磁感线均通过磁铁内部形成闭合曲线理解不深，容易出错。

例题2. 磁感应强度为B的匀强磁场方向水平向右，一面积为S的线圈abcd如图所示放置，平面abcd与竖直面成θ角。

将abcd绕ad轴转180º角，则穿过线圈的磁通量的变化量为（）A. 0B. 2BSC. 2BSc osθD. 2BSs inθ解析：C部分学生由于不理解关于穿过一个面的磁通量正负的规定而出现错误。

（二）等效分析法在空间问题中的应用例题3. 一个可自由运动的线圈L1和一个固定的线圈L2互相绝缘垂直放置，且两个圆线圈的圆心重合，当两线圈都通过如图所示的电流时，则从左向右看，线圈L1将（）A. 不动B. 顺时针转动C. 逆时针转动D. 向纸外平动解析：C 本题可把L1、L2等效成两个条形磁铁，利用同名磁极相斥，异名磁极相吸，即可判断出L1将逆时针转动。

（三）安培力作用下的平衡问题例题4. 一劲度系数为k的轻质弹簧，下端挂有一匝数为n的矩形线框abcd，bc边长为l。

线框的下半部处在匀强磁场中，磁感应强度大小为B，方向与线框平面垂直，在图中垂直于纸面向里。

线框中通以电流I，方向如图所示。

开始时线框处于平衡状态。

令磁场反向，磁感应强度的大小仍为B，线框达到新的平衡。

在此过程中线框位移的大小＝__________，方向_____________。

解析：，向下。

本题为静力学与安培力综合，把安培力看成静力学中按性质来命名的一个力进行受力分析，是本题解答的基本思路。

例题5. 如图所示，两平行光滑导轨相距为20cm，金属棒MN质量为10g，电阻R＝8Ω，匀强磁场的磁感应强度B的方向竖直向下，大小为0.8T，电源电动势为10V，内阻为1Ω。

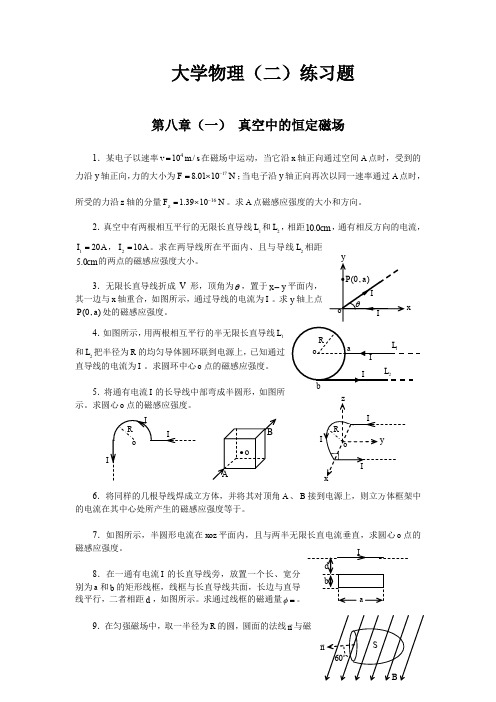
大学物理（二）练习题第八章（一） 真空中的恒定磁场1．某电子以速率410/v m s =在磁场中运动，当它沿x 轴正向通过空间A 点时，受到的力沿y 轴正向，力的大小为178.0110F N -=⨯；当电子沿y 轴正向再次以同一速率通过A 点时，所受的力沿z 轴的分量161.3910z F N -=⨯。

求A 点磁感应强度的大小和方向。

2．真空中有两根相互平行的无限长直导线1L 和2L ，相距10.0cm ，通有相反方向的电流，120I A =，210I A =。

求在两导线所在平面内、且与导线2L 相距5.0cm 的两点的磁感应强度大小。

3．无限长直导线折成V 形，顶角为θ，置于x y -平面内，其一边与x 轴重合，如图所示，通过导线的电流为I 。

求y 轴上点(0,)P a 处的磁感应强度。

4．如图所示，用两根相互平行的半无限长直导线1L 和2L 把半径为R 的均匀导体圆环联到电源上，已知通过直导线的电流为I 。

求圆环中心o 点的磁感应强度。

5．将通有电流I 的长导线中部弯成半圆形，如图所示。

求圆心o 点的磁感应强度。

6．将同样的几根导线焊成立方体，并将其对顶角A 、B的电流在其中心处所产生的磁感应强度等于。

7．如图所示，半圆形电流在xoz 平面内，且与两半无限长直电流垂直，求圆心o 点的磁感应强度。

8．在一通有电流I 的长直导线旁，放置一个长、宽分别为a 和b 的矩形线框，线框与长直导线共面，长边与直导线平行，二者相距d ，如图所示。

求通过线框的磁通量φ=。

9．在匀强磁场中，取一半径为R 的圆，圆面的法线n 与磁xnB感应强度B 成o 60角，如图所示，则通过以该圆周为边线的任意曲面S 的磁通量φ=。

10．在真空中，有两个半径相同的圆形回路1L 、2L ，圆周内都有稳恒电流1I 、2I ，其分布相同。

在图(b)中，回路2L 外还有稳恒电流3I ，1P 、2P 为两圆形回路上的对应点，如图所示，则下列表达式正确的是(A) 12L L B dl B dl ⋅=⋅⎰⎰，12PP B B =； (B)12L L B dl B dl ⋅≠⋅⎰⎰，12PP B B =；(C)12L LB dl B dl ⋅=⋅⎰⎰，12P P B B ≠；(D)12L L B dl B dl ⋅≠⋅⎰⎰，12PP B B ≠.[ ]11．如图所示，在圆形电流I 所在平面内，选取一同心圆形闭合回路L ，则由安培环路定理看出，以下结论正确的是(A)0LB dl ⋅=⎰，且环路L 上任一点，0B =；(B) 0LB dl ⋅=⎰，且环路L 上任一点，0B ≠；(C)0LB dl ⋅≠⎰，且环路L 上任一点，0B ≠；(D)0LB dl ⋅≠⎰，且环路L 上任一点，B =常量。

大学物理磁场试题及答案一、选择题（每题2分，共10分）1. 磁场的基本特性是（）。

A. 有方向性B. 有大小和方向C. 只有方向性D. 只有大小答案：B2. 根据安培环路定理，穿过闭合回路的磁通量与（）。

A. 回路的面积成正比B. 回路的面积成反比C. 回路的面积无关D. 回路的面积的平方成正比答案：C3. 磁感应强度的方向是（）。

A. 电流方向B. 电流方向的相反方向C. 垂直于电流方向D. 与电流方向成任意角度答案：C4. 磁通量的大小由（）决定。

A. 磁场的强度B. 面积的大小C. 磁场与面积的夹角D. 以上所有因素答案：D5. 磁感应强度的单位是（）。

A. 特斯拉B. 高斯C. 安培/米D. 以上都是答案：D二、填空题（每题2分，共10分）1. 一个长直导线产生的磁场，其磁感应强度与导线距离的平方成______。

答案：反比2. 地球的磁场可以近似看作是一个______。

答案：条形磁铁3. 根据洛伦兹力公式，一个带电粒子在磁场中运动时受到的力的方向与______。

答案：磁场方向和粒子速度方向都垂直4. 磁通量的基本单位是______。

答案：韦伯5. 磁感应强度的定义式为______。

答案：B = F/IL三、计算题（每题10分，共30分）1. 一个长为L的直导线，通有电流I，求在距离导线r处的磁感应强度。

答案：B = (μ₀I)/(2πr)2. 一个半径为R的圆形线圈，通有电流I，求其轴线上距离线圈中心d处的磁感应强度。

答案：B = (μ₀I)/(2R² + d²)^(3/2)3. 一个长为L的直导线，通有电流I，求在距离导线r处的磁通量，假设导线上方有一面积为A的平面与磁场垂直。

答案：Φ = B * A = (μ₀I * A)/(2πr)四、简答题（每题5分，共10分）1. 简述磁感应强度和磁通量的区别。

答案：磁感应强度是描述磁场强弱和方向的物理量，其大小和方向由磁场本身决定，与测试电荷无关。

第八章 磁场 填空题 （简单）1、将通有电流为I 的无限长直导线折成1/4圆环形状，已知半圆环的半径为R ，则圆心O 点的磁感应强度大小为08I Rμ 。

2、磁场的高斯定理表明磁场是 无源场 。

3、只要有运动电荷，其周围就有 磁场 产生；4、（如图）无限长直导线载有电流I 1，矩形回路载有电流I 2，I 2回路的AB 边与长直导线平行。

电 流I 1产生的磁场作用在I 2回路上的合力F 的大小为01201222()I I L I I La ab μμππ-+，F 的方向 水平向左 。

（综合）5、有一圆形线圈，通有电流I ，放在均匀磁场B 中，线圈平面与B 垂直，则线圈上P 点将受到 安培 力的作用，其方向为 指向圆心 ，线圈所受合力大小为 0 。

（综合）6、∑⎰==⋅n i i lI l d B 00μ是 磁场中的安培环路定理 ，它所反映的物理意义是 在真空的稳恒磁场中，磁感强度B 沿任一闭合路径的积分等于0μ乘以该闭合路径所包围的各电流的代数和。

7、磁场的高斯定理表明通过任意闭合曲面的磁通量必等于 0 。

8、电荷在磁场中 不一定 （填一定或不一定）受磁场力的作用。

9、磁场最基本的性质是对 运动电荷、载流导线 有力的作用。

10、如图所示，在磁感强度为B 的均匀磁场中，有一半径为R 的半球面，B 与半球面轴线的夹角为α。

求通过该半球面的磁通量为2cos B R πα-。

（综合） 12、一电荷以速度v 运动，它既 产生 电场，又 产生 磁场。

(填“产生”或“不产生”)13、一电荷为+q ，质量为m ，初速度为0υ的粒子垂直进入磁感应强度为B 的均匀磁场中，粒子将作 匀速圆周 运动，其回旋半径R=0m Bqυ，回旋周期T=2mBq π 。

14、把长直导线与半径为R 的半圆形铁环与圆形铁环相连接（如图a 、b 所示），若通以电流为I ，则 a 圆心O4题图 5题图的磁感应强度为___0__________； 图b 圆心O 的磁感应强度为04IRμ。

习题题10.1：如图所示，两根长直导线互相平行地放置，导线内电流大小相等，均为I = 10 A，方向相同，如图所示，求图中M、N两点的磁感强度B的大小和方向（图中r0 = 0.020 m）。

题10.2：已知地球北极地磁场磁感强度B的大小为6.0 105 T。

如设想此地磁场是由地球赤道上一圆电流所激发的（如图所示），此电流有多大？流向如何？题10.3：如图所示，载流导线在平面内分布，电流为I，它在点O的磁感强度为多少？题10.4：如图所示，半径为R的木球上绕有密集的细导线，线圈平面彼此平行，且以单层线圈覆盖住半个球面，设线圈的总匝数为N，通过线圈的电流为I，求球心O处的磁感强度。

题10.5：实验中常用所谓的亥姆霍兹线圈在局部区域内获得一近似均匀的磁场，其装置简图如图所示，一对完全相同、彼此平行的线圈，它们的半径均为R ，通过的电流均为I ，且两线圈中电流的流向相同，试证：当两线圈中心之间的距离d 等于线圈的半径R 时，在两线圈中心连线的中点附近区域，磁场可看成是均匀磁场。

（提示：如以两线圈中心为坐标原点O ，两线圈中心连线为x 轴，则中点附近的磁场可看成是均匀磁场的条件为x B d d = 0；0d d 22=xB ） 题10.6：如图所示，载流长直导线的电流为I ，试求通过矩形面积的磁通量。

题10.7：如图所示，在磁感强度为B 的均匀磁场中，有一半径为R 的半球面，B 与半球面轴线的夹角为α，求通过该半球面的磁通量。

题10.8：已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热。

电流在导线横截面上均匀分布。

求：（1）导线内、外磁感强度的分布；（2）导线表面的磁感强度。

题10.9：有一同轴电缆，其尺寸如图所示，两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑。

试计算以下各处的磁感强度：（1）r <R 1；（2）R 1<r <R 2；（3）R 2<r <R 3；（4）r >R 3。

习题题10.1：如图所示，两根长直导线互相平行地放置，导线电流大小相等，均为I = 10 A，方向相同，如图所示，求图中M、N两点的磁感强度B的大小和方向（图中r0 = 0.020 m）。

题10.2：已知地球北极地磁场磁感强度B的大小为6.0⨯10-5 T。

如设想此地磁场是由地球赤道上一圆电流所激发的（如图所示），此电流有多大？流向如何？题10.3：如图所示，载流导线在平面分布，电流为I，它在点O的磁感强度为多少？题10.4：如图所示，半径为R的木球上绕有密集的细导线，线圈平面彼此平行，且以单层线圈覆盖住半个球面，设线圈的总匝数为N，通过线圈的电流为I，求球心O处的磁感强度。

题10.5：实验中常用所谓的亥姆霍兹线圈在局部区域获得一近似均匀的磁场，其装置简图如图所示，一对完全相同、彼此平行的线圈，它们的半径均为R，通过的电流均为I，且两线圈中电流的流向相同，试证：当两线圈中心之间的距离d等于线圈的半径R时，在两线圈中心连线的中点附近区域，磁场可看成是均匀磁场。

（提示：如以两线圈中心为坐标原点O ，两线圈中心连线为x 轴，则中点附近的磁场可看成是均匀磁场的条件为x B d d = 0；0d d 22=xB ） 题10.6：如图所示，载流长直导线的电流为I ，试求通过矩形面积的磁通量。

题10.7：如图所示，在磁感强度为B 的均匀磁场中，有一半径为R 的半球面，B 与半球面轴线的夹角为α，求通过该半球面的磁通量。

题10.8：已知10 mm 2裸铜线允许通过50 A 电流而不会使导线过热。

电流在导线横截面上均匀分布。

求：（1）导线、外磁感强度的分布；（2）导线表面的磁感强度。

题10.9：有一同轴电缆，其尺寸如图所示，两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑。

试计算以下各处的磁感强度：（1）r <R 1；（2）R 1<r <R 2；（3）R 2<r <R 3；（4）r >R 3。