大学物理作业解答

《大学物理III 》课后作业（解答）第一部分：力学简答题：1. 用文字描述牛顿第一定律。

它的另一个名称是什么？解答：任何物体在不受外力作用时，将保持静止或匀速直线运动状态。

另一个名称是“惯性定律”。

2．用文字描述牛顿第三定律。

作用力和反作用力有什么特点？解答：当物体A 以力1作用在物体B 上时，B 同时也有力2作用在A 上，这两个力大小相等，方向相反，在同一条直线上，即12-=。

作用力和反作用力有如下三个特点：（1）它们成对出现，关系一一对应；（2）它们分别作用在两个不同物体上，因而不是一对平衡力；（3）它们的性质相同，比如同为引力、摩擦力、弹力，等等。

3．假设雨滴从1000米的高空云层中落到地面。

请问可否用自由落体运动描述雨滴的运动？并简述理由。

解答：不能。

如果我们用自由落体运动来描述雨滴运动（即忽略空气阻力），那么雨滴从1000米高空落到地面时，它的速度将达到m/s 1402==gH v ！这个速度已经达到普通手枪的子弹出射速度，足以对地面上的人畜造成致命伤害。

而生活经验告诉我们，雨滴落到我们头上并不会造成严重伤害，所以它落到地面的速度远远小于140m/s 。

事实上，因为空气阻力的存在（通常跟雨滴的速度大小成正比），雨滴将有一个收尾速度，它落到地面时做匀速直线运动，速度约为10-20m/s ，不会对地面生物造成致命伤害。

4．用文字描述质点系的动量守恒定律。

解答：当一个质点系所受合外力为零时，系统内各质点间动量可以交换，但系统的总动量保持不变。

5. 如图，一根质量为m 、长l 的刚性杆子竖直悬挂，顶点固定在天花板O 点，杆子可绕O 点自由转动。

一个质量也为m 的物块（质点）以水平速度0v跟杆子的下端碰撞，并粘在一起。

在这个碰撞过程中，物体和杆子组成系统的动量是否守恒？角动量是否守恒？并简述理由。

解答：动量不守恒，因为在碰撞瞬间物体和杆子系统在O 点受到很大外力，其产生的冲量不可忽略；角动量守恒，因为系统所受一切力的对O 点力矩为零，包括上述的巨大外力。

大学物理力学一、二章作业答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第一章 质点运动学一、选择题1、一质点在xoy 平面内运动，其运动方程为2,ct b y at x +==，式中a 、b 、c 均为常数。

当运动质点的运动方向与x 轴成450角时，它的速率为[ B ]。

A ．a ；B ．a 2；C ．2c ；D ．224c a +。

2、设木块沿光滑斜面从下端开始往上滑动，然后下滑，则表示木块速度与时间关系的曲线是图1-1中的[ D ]。

3、一质点的运动方程是j t R i t R rωωsin cos +=，R 、ω为正常数。

从t ＝ωπ/到t =ωπ/2时间内该质点的路程是[ B ]。

A ．2R ；B ．R π；C ． 0；D ．ωπR 。

4、质量为0.25kg 的质点，受i t F =(N)的力作用，t =0时该质点以v=2j m/s 的速度通过坐标原点，该质点任意时刻的位置矢量是[ B ]。

A ．22t i +2j m ； B ．j t i t2323+m ；C ．j t i t343243+； D ．条件不足，无法确定。

二、填空题1、一质点沿x 轴运动，其运动方程为225t t x -+=（x 以米为单位，t 以秒为单位）。

质点的初速度为 2m/s ，第4秒末的速度为 -6m/s ，第4秒末的加速度为 -2m/s 2 。

2、一质点以π（m/s ）的匀速率作半径为5m 的圆周运动。

该质点在5s 内的平均速度的大小为 2m/s ，平均加速度的大小为 22m /5s π 。

3、一质点沿半径为0.1m 的圆周运动，其运动方程为22t +=θ（式中的θ以弧度计，t 以秒计），质点在第一秒末的速度为 0.2m/s ，切向加速度为 0.2m/s 2 。

4、一质点沿半径1m 的圆周运动，运动方程为θ=2+3t 3，其中θ以弧度计，t 以秒计。

T =2s 时质点的切向加速度为 36m/s 2 ；当加速度的方向和半径成45º角时角位移是 38rad 。

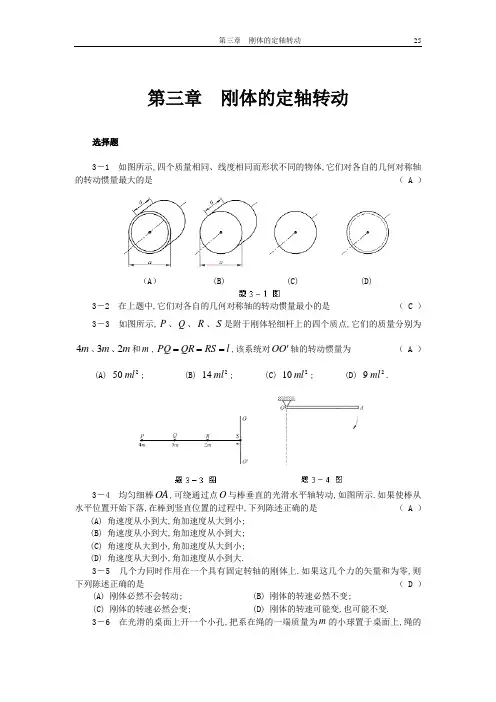
第三章刚体的定轴转动选择题3－1 如图所示,四个质量相同、线度相同而形状不同的物体,它们对各自的几何对称轴的转动惯量最大的是（ A ）（A） (B) (C) (D)3－2 在上题中,它们对各自的几何对称轴的转动惯量最小的是（ C ）3－3 如图所示,P、Q、R、S是附于刚体轻细杆上的四个质点,它们的质量分别为4m、3m、2m和m,PQ QR RS l===,该系统对O O'轴的转动惯量为（ A ）(A) 29m l.10m l; (D) 214m l; (C) 250m l; (B) 23－4 均匀细棒O A,可绕通过点O与棒垂直的光滑水平轴转动,如图所示.如果使棒从水平位置开始下落,在棒到竖直位置的过程中,下列陈述正确的是（ A ）(A) 角速度从小到大,角加速度从大到小;(B) 角速度从小到大,角加速度从小到大;(C) 角速度从大到小,角加速度从大到小;(D) 角速度从大到小,角加速度从小到大.3－5 几个力同时作用在一个具有固定转轴的刚体上.如果这几个力的矢量和为零,则下列陈述正确的是（ D ）(A) 刚体必然不会转动; (B) 刚体的转速必然不变;(C) 刚体的转速必然会变; (D) 刚体的转速可能变,也可能不变.3－6 在光滑的桌面上开一个小孔,把系在绳的一端质量为m的小球置于桌面上,绳的另一端穿过小孔而执于手中.设开始时使小球以恒定的速率v 在水平桌面上作半径为1r 的圆周运动,然后拉绳使小球的轨道半径缩小为2r ,新的角速度2ω和原来的角速度1ω的关系为（ B ） (A) 1212r r ωω⎛⎫ ⎪⎝⎭=; (B) 21212r r ωω⎛⎫⎪⎝⎭=;(C) 2211r r ωω⎛⎫ ⎪⎝⎭=; (D) 22211r r ωω⎛⎫⎪⎝⎭=.3－7 在上题中,新的动能和原来的动能之比为 （ A ）(A) 212r r ⎛⎫ ⎪⎝⎭; (B) 12r r ; (C) 21rr ; (D) 221r r ⎛⎫ ⎪⎝⎭.3－8 刚体绕定轴高速旋转时,下列陈述正确的是 （ D ）(A) 它受的外力一定很大; (B) 它受的外力矩一定很大;(C) 它的角加速度一定很大; (D) 它的角动量和转动动能一定很大. 3－9 芭蕾舞演员绕通过脚尖的竖直轴旋转,当她伸长手臂时的转动惯量为J ,角速度为ω.她将手臂收回至前胸时,转动惯量减小为3J ,此时她的角速度为 （ A ）(A) 3ω; (D) 13ω.3－10 三个完全相同的转轮绕一公共轴旋转.它们的角速度大小相同,但其中一轮的转动方向与另外两个轮相反.今沿轴的方向施力,将三者靠在一起,使它们获得相同的角速度.此时靠在一起后系统的动能与原来三转轮的总动能相比是 （ B ）(A) 减少到13; (B) 减少到19;(C) 增大到3倍; (D) 增大到9倍.计算题3－11 一电动机的电枢转速为11800r min -⋅,当切断电源后,电枢经20s 停下.求:(1) 切断电源后电枢转了多少圈;(2) 切断电源后10s 时,电枢的角速度以及电枢边缘上一点的线速度、切向加速度和法向加速度(设电枢半径为10cm ).解 (1) 切断电源时,电枢的转速为11018002πrad s60πrad s60ω--⨯=⋅=⋅电枢的平均角加速度为22060πrad s3.0πrad s20tωα----==⋅=-⋅∆由2202ωωαθ-=∆,且0ω=,可得切断电源后电枢转过的角度为()()22060πrad 600πrad 223πωθα--∆===⨯-转过的圈数为600πr 300r 2π2πN θ∆===(2) 切断电源后10s 时,电枢的角速度为()11060π 3.0π10rad s30πrad s t ωωα--=+=-⨯⋅=⋅此时电枢边缘上一点的线速度、切向加速度和法向加速度分别为()111222t 222222n 0.1030πm s3.0πm s9.42m s0.10 3.0πm s0.30πm s0.942m s0.1030πm s90πm s888m sr a r a r ωαω---------==⨯⋅=⋅=⋅==-⨯⋅=-⋅=-⋅==⨯⋅=⋅=⋅v3－12 一飞轮由直径为0.30m 、厚度为22.010m -⨯的圆盘和两个直径为0.10m 、长为28.010m -⨯的圆柱体组成.设飞轮的密度为337.810kg m -⨯⋅,求飞轮对转轴的转动惯量.解 飞轮上的圆盘的半径为10.15m r =,圆柱体的半径为20.05m r =. 飞轮上的圆盘质量为2322111π7.810π0.15 2.010kg 11.0kg m r h ρ-==⨯⨯⨯⨯=圆柱体的质量为2322222π7.810π0.058.010kg 4.90kgm r h ρ-==⨯⨯⨯⨯⨯=飞轮的转动惯量是圆盘和两个圆柱体的转动惯量之和为22222211221111.00.15 4.900.05kg m 0.136kg m 22J m r m r ⎛⎫=+=⨯⨯+⨯⋅=⋅ ⎪⎝⎭3－13 如图所示,质量分别为2m 、3m 和4m 的三个小球,用长均为l 、质量均为m 的三根均匀细棒相连,如图所示(小球的半径r l <<,可视为质点).求该物件对通过点O 垂直于图面的转轴的转动惯量.解 该物件的转动惯量是三个小球和三根细棒的转动惯量之和为2222212343103J m l m l m l m l m l =+++⨯=3－14 细棒长为l ,质量为m ,设转轴通过棒上离中心为h 的一点并与棒垂直.求棒对此轴的转动惯量.解 由平行轴定理,细棒的转动惯量为22222c 111212J J m h m l m h m l h ⎛⎫=+=+=+ ⎪⎝⎭3－15 一个半径为R 质量为m 的均匀圆盘,挖去直径为R 的一个圆孔,如图所示.求剩余部分对通过圆心O 且与盘面垂直的轴的转动惯量.解 开孔圆盘的转动惯量等于完整圆盘的转动惯量减去位于圆孔部位的被挖去的小圆盘的转动惯量:2222111322424232m R m R J m R m R ⎡⎤⎛⎫⎛⎫=-+=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦ 3－16 如图所示,某飞轮的直径为0.50m 、转动惯量为22.4k g m ⋅、转速为311.010r min-⨯⋅.如果制动时闸瓦对轮的压力为490N ,闸瓦与轮之间的滑动摩擦因数为0.4,求制动后飞轮转多少圈才停止.解 制动前,飞轮的转速为31102π 1.010rad s105rad s60ω--⨯⨯=⋅=⋅飞轮所受的制动力矩为n 0.44900.25N m 49N m M F R μ=-=-⨯⨯⋅=-⋅根据转动定律,M J α=,可得制动后飞轮的角加速度为2249rad s20.4rad s2.4M J α---==⋅=-⋅由2202ωωαθ-=∆,且0ω=,可得制动后飞轮转过角度为220105rad 270rad 22(20.4)ωθα--∆===⨯-转过的圈数为270r 43.0r 2π2πN θ∆===3－17 如图所示,一物体质量为5kg ,从一倾角为o 37的斜面滑下,物体与斜面的摩擦因数为0.25.一滑轮装在固定轴O 处,轻绳的一端绕在滑轮上,另一端与物体相连.若滑轮可视为是实心圆盘,其质量为20kg 、半径为0.2m ,绳与轮间无相对滑动,且轮轴的摩擦阻力矩忽略不计.求：(1) 物体沿斜面下滑的加速度; (2) 绳中的张力.解 物体和滑轮的示力图以及坐标选取如图所示.图中P 为重力,N F 为正压力,r F 为摩擦力,T F 为张力,T T F F '=.O x 轴沿斜面向下,Oy 垂直于斜面.设物体的质量为1m ,滑轮的质量为2m ,滑轮的半径为r .对物体,根据牛顿第二定律,在O x 和Oy 方向分别有o1T r 1sin 37m g F F m a --=oN 1cos 370F m g -=重力2P 和轮轴对滑轮的压力N 2F 均通过转轴,对转轴的力矩为零.以垂直纸面向里为正方向,滑轮所受的力矩为T T M F r F r '=⋅=⋅.对滑轮,根据转动定律,有T F r J α⋅=而a r α=r N F F μ=2212J m r =联立解以上方程,可得物体沿斜面下滑的加速度和绳中的张力分别为()oo11222sin 37cos 3712345 0.259.8 m s 1.31 m s1555202m a gm m μ--=-+⎛⎫=-⨯⨯⨯⋅=⋅ ⎪⎝⎭+⨯T 21120 1.31 N 13.1 N 22F Jm a rα===⨯⨯=3－18 如图所示,长为l 、质量为m 的均匀细棒可绕点O 转动.此棒原先静止在竖直位置,受微小扰动而倒下.若不计摩擦和空气阻力,求细棒倒至与竖直位置成θ角时的角加速度和角速度.解 细棒的倒下,可看成定轴转动,其转轴通过地面上细棒端点,垂直于细棒的转动平面.在细棒倒下的过程中,细棒与地球组成的系统机械能守恒.以地面为势能零点,设细棒倒至与竖直方向成θ角时,角速度为ω,有21cos 222l l J m gm gωθ+=而213J m l =由此可得,角速度为ω=只有细棒所受的重力对转轴有力矩.以垂直纸面向里为正方向,细棒倒至与竖直方向成θ角时,重力对转轴的力矩为sin 2l M m g θ=.设此时的角加速度为α,则对细棒,根据转动定律,有sin 2l m gJ θα= 将213J m l =代入上式,可得角加速度为3sin 2g lαθ=3－19 如图所示,两个物体质量分别为1m 和2m .定滑轮的质量为m 、半径为R ,可视为圆盘.已知2m 与桌面间的摩擦因数为μ.设轻绳与轮间无相对滑动,且可不计滑轮轴的摩擦力矩,求1m 下落的加速度和滑轮两边绳中的张力.解 两个物体和滑轮的示力图以及坐标选取如图所示.图中P 为重力,N F 为正压力,r F 为摩擦力,T F 为张力,T1T1F F '=,T 2T 2F F '=.O x 轴水平向右,Oy 轴竖直向下.两个物体的加速度虽方向不同,但大小相同,12a a a ==.对物体1m ,根据牛顿第二定律,在Oy 方向有1T 11m g F m a -=对物体2m ,根据牛顿第二定律,在O x 方向有T 2r 2F F m a -=滑轮所受的重力和转轴对滑轮的压力都通过转轴,对转轴的力矩为零.以垂直纸面向里为正方向,滑轮所受的力矩为T 1T 2M F R F R =-.对滑轮,根据转动定律,有T 1T 2F R F R J α-=而212J m R =a R α=r 2F m gμ=联立解以上方程,可得物体的加速度与绳中的张力分别为()1212222m m a g m m mμ-=++()2T 11122122m m F m gm m m μ++=++()1T 22122122m m F m gm m mμ++=++3－20 一圆盘状的均匀飞轮,其质量为100kg 、半径为0.5m ,绕几何中心轴转动.在30s 内,由起始转速13000r m in-⋅均匀地减速至11000r m in -⋅.求阻力矩所做的功.解 飞轮初、末角速度分别为1102π3000rad s100πrad s60ω--⨯=⋅=⋅112π1000100rad sπrad s603ω--⨯=⋅=⋅飞轮的转动惯量为2222111000.5kg m 12.5kg m 22J m R ==⨯⨯⋅=⋅根据动能定理理,外力矩对飞轮所做的功等于飞轮转动动能的增量,可得在飞轮减速的过程中,阻力矩对飞轮所做的功为()222200225111()2221100π 12.5100πJ 5.4810J23A J J J ωωωω=-=-⎡⎤⎛⎫=⨯⨯-=-⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦3－21 质量为m '、半径为R 的转台,可绕过中心的竖直轴转动.质量为m 的人站在转台的边缘.最初人和转台都静止,后来人在转台的边缘开始跑动.设人的角速度(相对于地面)为ω,求转台转动的角速度(转台可看成质量均匀分布的圆盘,并忽略转轴处的摩擦力矩和空气的阻力).解 人和转台组成的系统对中心轴角动量守恒.以人的角速度的方向为正方向,设转台的角速度为1ω,有210J m R ωω+=而212J m R '=由此可得12m m ωω-='式中的负号表明,转台的转动方向与人的转动方向相反.3－22 如图所示,一个转动惯量为J 、半径为R 的圆木盘,可绕通过中心垂直于圆盘面的轴转动.今有一质量为m 的子弹,在距转轴2R 的水平方向以速度0v 射入,并嵌在木盘边缘.求子弹嵌入后木盘转动的角速度.解 子弹和木盘组成的系统,对转轴角动量守恒.以垂直于纸面向外为正方向,设子弹嵌入后,木盘转动的角速度为ω,有2()2R J m R m ω+=v由此可得022()m R J m R ω=+v3－23 如图所示,一均匀细棒长为l 、质量为m ,可绕经过端点O 的水平轴转动.棒被拉到水平位置由静止轻轻放开,下落至竖直位置时,下端与放在地面上的静止物体相撞.若物体的质量也为m ,物体与地面间的摩擦因数为μ,物体滑动s 距离后停止.求: (1) 棒与物体碰撞后,物体的速度;(2) 棒与物体碰撞后,棒的角速度.解 (1)根据动能定理,摩擦力对滑块所做的功等于滑块动能的增量.设物体因碰撞而获得的速度为v ,有2102m gs m μ-=-v由此可得=v (2) 细棒下落的过程中,细棒与地球组成的系统机械能守恒定律.以地面为势能零点,设细棒下落至竖直位置时的角速度为0ω,有20122l J m gω=而213J m l =由此可得0ω=.碰撞过程中角动量守恒.以垂直纸面向外为正方向,设碰撞后,细棒的角速度为ω,有0J m l J ωω+=v将213J m l =、=v 和0ω=代入上式,可得lω=若0ω>,碰撞后细棒继续向右转动, 若0ω<,碰撞后细棒向左转动.。

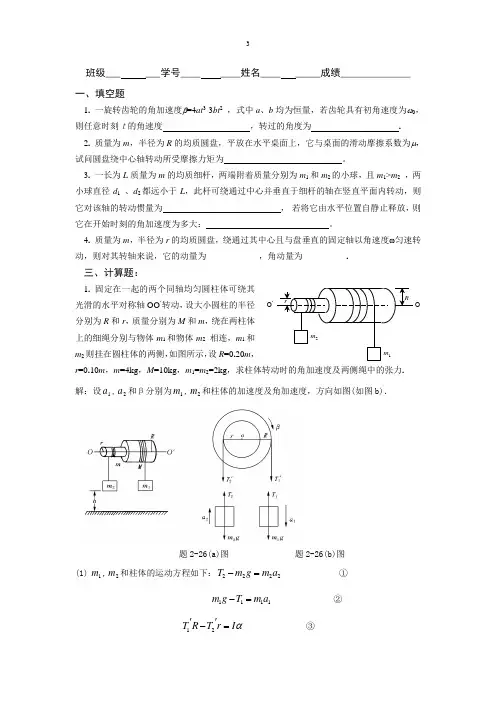
班级___ ___学号____ ____姓名____ _____成绩______________ 一、填空题1. 一旋转齿轮的角加速度β=4at 3-3bt 2 ，式中a 、b 均为恒量，若齿轮具有初角速度为ω0，则任意时刻ｔ的角速度 ，转过的角度为 .2. 质量为m ，半径为R 的均质圆盘，平放在水平桌面上，它与桌面的滑动摩擦系数为μ，试问圆盘绕中心轴转动所受摩擦力矩为 。

3. 一长为L 质量为m 的均质细杆，两端附着质量分别为m 1和m 2的小球，且m 1>m 2 ，两小球直径d 1 、d 2都远小于L ，此杆可绕通过中心并垂直于细杆的轴在竖直平面内转动，则它对该轴的转动惯量为 ， 若将它由水平位置自静止释放，则它在开始时刻的角加速度为多大： 。

4. 质量为m ，半径为r 的均质圆盘，绕通过其中心且与盘垂直的固定轴以角速度ω匀速转动，则对其转轴来说，它的动量为____________，角动量为__________.三、计算题：1. 固定在一起的两个同轴均匀圆柱体可绕其光滑的水平对称轴OO ’转动，设大小圆柱的半径分别为R 和r ，质量分别为M 和m ，绕在两柱体上的细绳分别与物体m 1和物体m 2 相连，m 1和m 2则挂在圆柱体的两侧，如图所示，设R =0.20m ，r =0.10m ，m =4kg ，M =10kg ，m 1=m 2=2kg ，求柱体转动时的角加速度及两侧绳中的张力. 解：设1a ,2a 和β分别为1m ,2m 和柱体的加速度及角加速度，方向如图(如图b)．题2-26(a)图 题2-26(b)图(1) 1m ,2m 和柱体的运动方程如下：2222a m g m T =- ①1111a m T g m =- ②12T R T r I α''-= ③rRO ’Om 2m 1式中 112221,,,T T T T a r a R αα''==== 而 222121mr MR I += 由上式求得122212222220.220.129.811100.2040.1020.2020.10226.13rad s Rm rm gI m R m r β--=++⨯-⨯=⨯⨯⨯+⨯⨯+⨯+⨯=⋅(2)由①式 22220.10 6.1329.820.8T m r m g α=+=⨯⨯+⨯=N 由②式11129.820.2. 6.1317.1T m g m R α=-=⨯-⨯⨯=N2. 计算题3-13图所示系统中物体的加速度．设滑轮为质量均匀分布的圆柱体，其质量为M ，半径为r ，在绳与轮缘的摩擦力作用下旋转，忽略桌面与物体间的摩擦，设1m ＝50kg ，2m ＝200 kg,M ＝15 kg, r ＝0.1 m解: 分别以1m ,2m 滑轮为研究对象，受力图如图(b)所示．对1m ,2m 运用牛顿定律，有a m T g m 222=- ① a m T 11= ②对滑轮运用转动定律，有α)21(212Mr r T r T =- ③又， αr a = ④联立以上4个方程，得 2212s m 6.721520058.92002-⋅=++⨯=++=M m m g m a题3-13(a)图 题3-13(b)图3. 如图质量为M ，长为L 的均匀直杆可绕O 轴在竖直平面内无摩擦地转动，开始时杆处于自由下垂位置，一质量为m 的弹性小球水平飞来与杆下端发生完全弹性碰撞，若M >3m ，且碰撞后，杆上摆的最大角度为θ=30，则求：(A)小球的初速度v 0，(B)碰撞过程中杆给小球的冲量. （教材）解: (1)设小球的初速度为0v ，棒经小球碰撞后得到的初角速度为ω，而小球的速度变为v ，按题意，小球和棒作弹性碰撞，所以碰撞时遵从角动量守恒定律和机械能守恒定律，可列式：mvl I l mv +=ω0 ①2220212121mv I mv +=ω ② 上两式中231Ml I =，碰撞过程极为短暂，可认为棒没有显著的角位移；碰撞后，棒从竖直位置上摆到最大角度o30=θ，按机械能守恒定律可列式：)30cos 1(2212︒-=lMg I ω ③ 由③式得 2121)231(3)30cos 1(⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡︒-=l g I Mgl ω 由①式 mlI v v ω-=0 ④ 由②式 mI v v 2202ω-= ⑤所以 22001)(2ωωmv ml I v -=-求得glmM m m Ml ml I l v +-=+=+=31232(6)311(2)1(220ωω(2)相碰时小球受到的冲量为 ⎰-=∆=0d mv mv mv t F由①式求得 ωωMl l I mv mv t F 31d 0-=-=-=⎰gl M 6)32(6--=负号说明所受冲量的方向与初速度方向相反．m v MOL。

电势、导体与※电介质中的静电场 （参考答案）班级： 学号： 姓名： 成绩：一 选择题1．真空中一半径为R 的球面均匀带电Q ，在球心O 处有一带电量为q 的点电荷，如图所示，设无穷远处为电势零点，则在球内离球心O 距离为r 的P 点处的电势为： （A ）r q04πε； （B ）)(041R Qrq+πε；（C ）r Qq 04πε+； （D ）)(041R qQ r q-+πε；参考：电势叠加原理。

[ B ] 2．在带电量为-Q 的点电荷A 的静电场中，将另一带电量为q 的点电荷B 从a 点移动到b ，a 、b 两点距离点电荷A 的距离分别为r 1和r 2，如图，则移动过程中电场力做功为：（A ）)(210114r r Q --πε； （B ）)(210114r r qQ-πε；（C ）)(21114r r qQ --πε； （D ）)(4120r r qQ --πε。

参考：电场力做功＝势能的减小量。

A=W a -W b ＝q(U a -U b ) 。

[ C ] 3．某电场的电力线分布情况如图所示，一负电荷从M 点移到N 点，有人根据这个图做出以下几点结论，其中哪点是正确的？（A ）电场强度E M ＜E N ； （B ）电势U M ＜U N ； （C ）电势能W M ＜W N ； （D ）电场力的功A ＞0。

[ C ]4．一个未带电的空腔导体球壳内半径为R ，在腔内离球心距离为d （d ＜R ）处，固定一电量为+q 的点电荷，用导线把球壳接地后，再把地线撤去，选无穷远处为电势零点，则球心O 处的点势为：（A ）0； （B ）d q04πε； （C ）-R q04πε； （D ）)(1140R dq-πε。

参考：如图，先用高斯定理可知导体内表面电荷为-q ，外表面无电荷（可分析）。

虽然内表面电荷分布不均，但到O 点的距离相同，故由电势叠加原理可得。

[ D ] ※5．在半径为R 的球的介质球心处有电荷+Q ，在球面上均匀分布电荷-Q ，则在球内外处的电势分别为：（A ）内r Q πε4+，外r Q04πε-； （B ）内r Qπε4+，0； 参考：电势叠加原理。

No.1 运动的描述一、选择题1. 一质点在平面上作一般曲线运动，其瞬时速度为v，瞬时速率为v ，某一段时间内的平均速度为v，平均速率为v ，它们之间的关系有 [ D ](A) v v v v ==, (B) v v v v =≠, (C) v v v v ≠≠,(D) v v v v ≠=,注意：①平均速度t r∆∆= v ，矢量。

②平均速率t ∆∆=sv ，标量。

③一般情况下，|||r |s ∆≠∆。

④瞬时速度tr ∆∆=→∆0t lim v 。

⑤瞬时速率|v |v=（即瞬时速率是瞬时速度的大小，这与平均速度和平均速率的关系不同） 2. 某物体的运动规律为kt tv -=d d ，式中的k 为大于零的常数。

当t ＝0时，初速为0v ，则速度v 与t 的函数关系是 [ B ](A) 0221v kt v += (B) 0221v kt v +-=注意：①求积分。

3. 一质点在平面上运动，已知质点位置矢量的表示式为j bt i at r 22+=（其中a 、b 为常量）则该质点作 [ B ] (A) 匀速直线运动 (B) 变速直线运动 (C) 抛物线运动 (D) 一般曲线运动 注意：①求导数。

②求运动方程。

4.一运动质点在某瞬时位于矢径),(y x r的端点处，其速度大小为 [ D ]（C ）tr d d( D)22)d d ()d d (ty tx +注意：①即求模长。

二、填空题★1. 一质点的运动方程为SI)(62t t x -=，则在t 由0至4 s 的时间间隔内，质点的位移大小为8m ，在t 由0到4 s 的时间间隔内质点走过的路程为 10 m 。

注意：①陷阱，4秒内并不是一直在往前，中间存在一个先去后返的过程。

2. ()()t t r t r ∆+与为某质点在不同时刻的位置矢量，试在两个图中分别画出三、计算题1.（p36 习题1.6）一质点在xy 平面上运动，运动函数84,22-==t y t x （采用国际单位制）。