i 1
2
解:
Xi
~
N (0,1), i
1,, n,
且 它 们 独 立.
n
i 1
( Xi )2 2
~
2 (n).
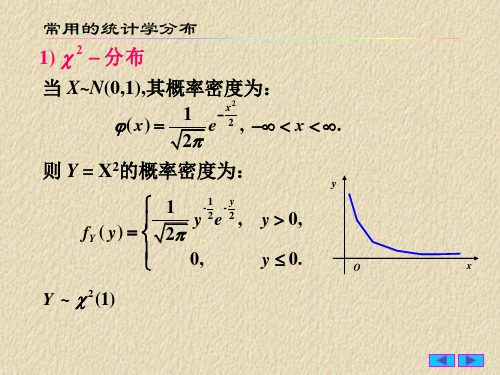
常用的统计学分布
2
对于给定的 (0 1),称满足条件:
P{
2
2
(
n)}
的点2 (n)为 2 (n)分布的上分位点。
常用的统计学分布
2 0.05
(8)
_1_5_.5_0_7_,
S/ n
(n 1)S 2 ~ t(n 1)
2 (n 1)
常用的统计学分布
定理3 设 X 1 , X 2 ,, X n1 与 Y1 ,Y2 ,Yn2 分别是具有
相同方差的两个正态总体N (1 , 2 ), N ( 2 , 2 )
的样本,且它们独立.
1 n1
1 n2
X
n1
Xi, Y
i 1
P{| t |> t (n)} = α
/2
tα (n) 为双侧分位数
t (n)
例 t0.05 (8) __2_.3_0_6_,
例 若 X ~ t(10), 且 1 使PX 1 0.05,则
1 t_0_.1_0_(1_0_)___1_._81_2_ .
若 X ~ t(10), 且 2 使PX 2 0.05,则
例 F0.95 (8,6) ____________ .
F0.9 (4,7) ______________ .
常用的统计学分布 设 T ~ t(n) ,则 T 2 ~ F (1, n)
证明: X ~ N (0, 1), Y ~ 2 (n), X,Y 独立
则