高一必修2立体几何--平行与垂直关系强化练习(含答案)

人教A版高中数学必修第二册8.6　空间直线、平面的垂直8.6.1　直线与直线垂直基础过关练题组一　求异面直线所成的角1.(2024安徽六安期中)如图,已知正四棱锥P-ABCD的所有棱长均为2,E为棱PA的中点,ABCD-A1B1C1D1中,E,F与直线AD1所成角的大小为在正方体ABCD-A(1)求异面直线CD1与BC1所成的角;(2)求证:MN∥平面ABCD.题组二　空间两条直线所成角的应用5.(多选题)(2024山东德州夏津第一中学月考)已知E,F 分别是三棱锥P-ABC 的棱PA,BC 的中点,且PC=6,AB=8.若异面直线PC 与AB 所成角的大小为60°,则线段EF 的长可能为( )A.7B.13C.5D.376.在长方体ABCD-A 1B 1C 1D 1中,底面ABCD 是边长为1的正方形,异面直线AB 与A 1C 所能力提升练在正四面体S-ABC 中3.4.(2024贵州凯里第一中学模拟)平面α过直三棱柱ABC-A 1B 1C 1的顶点B 1,平面α∥平面ABC 1,平面α∩平面BB 1C 1C=l,且AA 1=AB=BC,AB ⊥BC,则A 1B 与l 所成角的正弦值为( )A.32 B.22 C.12 D.335.已知正三棱柱ABC-A 1B 1C 1的侧面积为12,当其外接球的表面积取最小值时,异面直线AC 1与B 1C 所成角的余弦值为 .题组二　异面直线所成角的应用6.(2024上海青浦高级中学期末)在棱长为1的正方体ABCD-A 1B 1C 1D 1中,P 为底面ABCD 内(包括边界)的动点,满足直线D 1P 与CC 1所成角的大小为π6,则线段DP 扫过的面积为( )A.π12B.π6C.π3D.π27.(2024广东阳江期末)在四面体A-BCD 中,AB=CD=1,BC=2,且AB ⊥BC,CD ⊥BC,异面直线AB 与CD 所成的角为π3,则该四面体外接球的表面积为 .8.(2022河南濮阳第一高级中学月考)在四棱柱ABCD-A 1B 1C 1D 1中,侧面都是矩形,底面ABCD 是菱形且AB=BC=23,∠ABC=120°,若异面直线A 1B 和AD 1所成的角为90°,求AA 1的长度.答案与分层梯度式解析8.6　空间直线、平面的垂直8.6.1　直线与直线垂直基础过关练1.B2.C3.A 5.BD 6.DPC,EO=1PC=1,在所以BB1∥平面AEF,平面DBB1,所以BB1又与直线AD1所成的角为连接B N,CN,因为点M为A1B1的中点,A1B1=AB,所以MB1=AN,又MB1∥AN,所以四边形ANB1M为平行四边形,所以AM∥B1N,所以异面直线AM与B1C所成的角为∠CB1N(或其补角),设∠CB1N=θ,在正△ABC中,由AB=4,可得CN=23,在直角△BNB1中,BB1=3,BN=2,所以B1N=22+32=13,在直角△BCB1中,BC=4,BB1=3,所以B1C=42+32=5,在△B 1CN 中,由余弦定理的推论可得cos θ=B 1C 2+B 1N 2-C N 22B 1C·B 1N=52+(13)2-(23)22×5×13=135.故选A.4.解析　(1)连接A 1B,A 1C 1,因为A 1D 1=BC 且A 1D 1∥BC,所以四边形A 1D 1CB 为平行四边形,所以CD 1∥A 1B,则∠A 1BC 1或其补角为异面直线CD 1与BC 1所成的角,易知A 1C 1=A 1B=BC 1,所以△A 1C 1B 为等边三角形,所以∠A 1BC 1=60°,所以异面直线CD 1与BC 1所成的角为60°.(2)证明:连接C 1D,BD,则N 为C 1D 的中点,又M 为BC 1的中点,所以MN ∥BD,又MN ⊄平面ABCD,BD ⊂平面ABCD,所以MN ∥平面ABCD.5.BD 如图,取AC 的中点H,连接EH,FH,因为E,F 分别为PA,BC 的中点,PC=6,AB=8,所以AB ∥HF,HE ∥PC,HF=4,HE=3,所以异面直线PC 与AB 所成的角即为∠EHF(或其补角),所以∠EHF=60°或∠EHF=120°.当∠EHF=60°时,根据余弦定理的推论得cos ∠EHF=HE 2+H F 2-E F 22HE ·HF =9+16−EF 224=12,解得EF=13;当∠EHF=120°时,根据余弦定理的推论得cos ∠EHF=HE 2+H F 2-E F 22HE ·HF =9+16−EF 224=-12,解得EF=37.故选BD.易错警示　通过立体图形无法直接判断∠EHF是锐角还是钝角,因此∠EHF可能是异面直线所成的角,也可能是其补角,所以需要进行分类讨论.6.D　∵AB∥DC,∴∠A1CD(或其补角)即为异面直线AB与A1C所成的角,由图可知∠A1CD为.锐角,∴∠A1CD=π3设DD1=x,连接A1D,则A1C=12+12+x2=2+x2,A1D=x2+1.在∴∴7.垂直于上底面于点D,则ADD∥O2A,1∴或其补角,当在当在Rt△ABD中,AB=BD2+A D2=2.综上,AB=2或AB=2.能力提升练1.A2.A3.C4.A 6.A1.A　取SM的中点E,连接EN,AE,如图,∵N是SB的中点,∴EN∥MB,EN=12MB,∴∠ANE或其补角即为异面直线BM与AN所成的角.设正四面体的棱长为4,∵M是SC的中点,N是SB的中点,△SAB和△SBC均为正三角形,∴BM⊥SC,AN⊥SB,且BM=AN=23,∴EN=3,在△ASE中,由余弦定理得AE2=SA2+SE2-2SA·SE·cos∠ASE=16+1-2×4×1×12=13,在△ANE中,由余弦定理的推论得cos∠ANE=AN2+N E2-A E22AN·NE =12+3−132×23×3=16,∴异面直线BM与AN所成角的余弦值为16.故选A.2.A　如图,过点A作AN∥OM,交圆O于点N,连接ON,PN,则∠PAN或其补角即为异面直线OM与AP所成的角,设AO=ON=1,易知∠OAN=∠ONA=∠AOM=30°,则AN=3,因为轴截面PAB为等腰直角三角形,所以PN=PA=2,在△APN中,由余弦定理的推论得cos∠PAN=PA2+A N2-P N22PA·AN =2+3−226=64,所以异面直线OM与AP所成角的余弦值为64.故选A.3.C　如图,连接AD1,AP,易得AD1∥BC1,所以∠AD1P(或其补角)即为异面直线D1P与BC1所成的角.设正方体的棱长为1,DP=x,x∈[0,1],在△AD 1P 中,AD 1=2,AP=D 1P=1+x 2,故cos ∠AD 1P=(2)2+(1+x 2)2-(1+x 2)222·1+x 2=221+x 2,∵x ∈[0,1],∴cos ∠AD 1P=221+x2∈又∠AD 1P 是△AD 1P 的内角,∴∠AD 1P 故选C.B 1则ABC 1,所以B 1C 2∥平面⊂由小题速解　因为平面α∥平面ABC 1,平面α∩平面BB 1C 1C=l,平面ABC 1∩平面BB 1C 1C=BC 1,所以l ∥BC 1,则A 1B 与l 所成的角为∠A 1BC 1(或其补角),下同解析.5.答案　514解析　设正三棱柱的底面边长为a,高为h,外接球的半径为R,由题意知3ah=12,即ah=4,易得△ABC 外接圆的半径r=a2sin π3=a3,则R 2=r 2+ℎ24=a 23+ℎ24≥aℎ3=43,当且仅当a=32h 时取等号,此时外接球的表面积最小.将三棱柱补成一个四棱柱,如图,连接DB 1,DC,则AC 1∥DB 1,∴∠DB 1C(或其补角)为异面直线AC 1与B 1C 所成的角,易得B 1C=DB 1=a 2+ℎ2,DC=3a,∴cos ∠DB 1C=2(a 2+ℎ2)-3a 22(a 2+ℎ2)=514.解题技法　补形平移是常用的一种作平行线的方法,一般是补一个相同形状的几何体,构成一个特殊的几何体,方便作平行线,如此题将三棱柱补成一个四棱柱.6.A 因为DD 1∥CC 1,所以直线D 1P 与CC 1所成的角即为DD 1与D 1P 所成的角,易知DD 1⊥PD,所以DD 1与D 1P 所成的角为∠DD 1P,即∠DD 1P=π6,故tan ∠DD 1P=DPDD 1=33,即DP=33,所以点P 的轨迹是以D 为圆心,33为半径的圆的四分之一,故线段DP 扫过的面积为14π×=π12.故选A.7.答案　16π3或8π解析　由题意,可以将四面体A-BCD 补成一个直三棱柱,如图所示.∵CD∥BE,∴直线AB与CD所成的角为∠ABE或其补角,∵异面直线AB与CD所成的角为π3,∴∠ABE=π3或∠ABE=2π3.设△ABE外接圆的半径为r,当∠ABE=π3时,AE=BE=AB=1,则2r=1sinπ3,解得r=33;当∠ABE=2π3时,AE=3,则则8.BC且A1D1=BC,所以A1B∥CD1,所成的角为∠AD1C,故∠AD1均为矩形,设在故。

北师大版高中数学必修第二册专题强化练8　空间中的平行关系1.(多选题)(2024云南保山腾冲第八中学期中)已知a,b是两条不重合的直线,α,β是两个不重合的平面,则下列说法中正确的是( )A.若α∩β=b,a⊂α,则a与β一定相交B.若α∥β,a⊂α,则a∥βAA.EG与BC1为异面直线 B.Ω有13条棱C.Ω有7个顶点 D.平面BC1D∥平面EFG4.(2023新疆乌鲁木齐模拟)如图,在长方体ABCD-A1B1C1D1中,A1EEB1=BFFB1=CGGC1=D1HHC1=2,则下列说法错误的是( )D.边) 于答案与分层梯度式解析专题强化练8　空间中的平行关系1.BC　对于A,若α∩β=b,a⊂α,则a∥β或a与β相交,A错误;对于B,若α∥β,a⊂α,则由面面平行的性质可得a∥β,B正确;对于C,若a∥b,b⊂α,则a∥α或a⊂α,故a平行于α内的无数条直线,C正确;对于D,若α∥β,a⊂α,b⊂β,则a∥b或a与b是异面直线,故D错误.故选BC.2.ABC　由三棱柱ABC-A1B1C1的性质可知平面ABC∥平面A1B1C1,又平面BCHG∩平面ABC=BC,平面BCHG∩平面A1B1C1=GH,所以BC∥GH,因为点E,F分别是AB,AC的中点,所以BC∥EF,故EF∥GH,A正确;由EF∥GH,EF⊂平面A1EF,GH⊄平面A1EF,得GH∥平面A1EF,B正确;因为GH经过△A1B1C1的重心,GH∥BC∥B1C1,所以GHBC =GHB1C1=23,易知EFBC=12,则GHEF=43,C正确;因为A1,E,B,B1四点共面,且A1E与BB1相交,所以平面A1EF与平面BCC1B1相交,D错误.故选ABC.3.ABD　对于A,因为EG⊂平面ACC1A1,C1∈平面ACC1A1且C1∉EG, B∉平面ACC1A1,故EG与BC1为异面直线,故A正确;对于B,几何体Ω的棱有A1D,A1C1,DC1,A1E,EG,EF,CC1,C1B,DB,FG,GC,CB,FB,共13条,故B正确;对于C,几何体Ω的顶点有A1,D,C1,E,G,C,B,F,共8个,故C错误;对于D,如图,取AB的中点H,连接A1H,DH,CH,因为AB=4AF,所以F是AH的中点,又D,G,E分别为所在棱的中点,所以EF∥A1H,FG∥CH,由A1D∥BH,A1D=BH,得四边形A1DBH为平行四边形,故A1H∥DB,则EF∥DB,又EF⊄平面BDC1,DB⊂平面BDC1,所以EF∥平面BDC1.易知DH∥BB1∥CC1,且DH=BB1=CC1,故四边形DC1CH为平行四边形,则C1D∥CH,故FG∥C1D,又GF⊄平面BDC1,DC1⊂平面BDC1,所以GF∥平面BDC1,又EF∩FG=F,EF,FG⊂平面EFG,所以平面EFG∥平面BDC1,故D正确.故选ABD.4.A　如图所示,连接A1B,D1C,BD,BD1,5.②如图2,延长MP交B1C1于点N1,过点N1作AM的平行线交A1B1于点S1,连接AS1,则所求截面为四边形AMN1S1;③如图3,延长MP交BB1于点N2,连接AN2,则所求截面为△AMN2.显然①②中的截面面积均大于或等于③中的截面面积,故只需考虑①②中的情况,根据对称性可知①②中的情况相同,故只考虑情况①即可.在①中,易知AM=22,AM ⊥MN,△SC 1N 为等腰直角三角形,设C 1N=x 0≤x ≤则长度),所以所求截面面积×==12x 4+2x +34,因为y=x 4,y=2x +34在0,,所以函数y=x 4+2x +34在0,,故S max =12×=22,故所求截面面积的最大值为22.6.解析　(1)交线l 如图所示.作法:在平面BDE 中过D 点作直线l ∥BE,则直线l 就是所求作的交线.理由:在圆柱OO'中,EF,BC 是母线,∴EF ∥BC,EF=BC,∴四边形EFCB 是平行四边形,∴EB ∥FC,又∵EB ⊄平面FCD,CF ⊂平面FCD,∴EB ∥平面FCD.∵交线l=平面FCD∩平面DBE,∴l ∥EB,∴过D 作直线l ∥EB,则直线l 就是所求作的交线.∵l ∥EB,l ⊄平面BEF,EB ⊂平面BEF,∴l ∥平面BEF.(2)证明:取EF的中点G,连接MG,NG,∵M,G分别是DE,EF的中点,∴MG∥DF,∵MG⊄平面DFC,DF⊂平面DFC,∴MG∥平面DFC,∴MG∥平面ABE,同理可证GN∥平面ABE,∵MG∩GN=G,MG,GN⊂平面MGN,∴平面MGN∥平面ABE,又∵MN⊂平面MGN,∴MN∥平面ABE.。

．平行与垂直综合问题．已知直线，和平面α，β满足⊥，⊥α，α⊥β，则()．⊥β．∥β或⊂β．⊥α．∥α或⊂α解析：在平面β内作直线垂直于α，β的交线，则由α⊥β得直线⊥α.又⊥α，所以∥.若⊂β，结合图形知，要满足题中限制条件，显然只能∥α或⊂α；同理⊄β，仍有∥α或⊂α.综上所述，正确．．若三个平面α，β，γ，之间有α∥γ，β⊥γ，则α与β()．垂直．平行．相交．以上三种可能都有．对于任意的直线与平面α相交，在平面α内不可能有直线，使与()．平行．相交．垂直．互为异面直线．给出以下四个命题，其中真命题有①②④(填序号)．①如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行；②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面；③如果两条直线都平行于一个平面，那么这两条直线互相平行；④如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．．已知平面α外不共线的三点，，，且∥α，则正确的结论是() ．平面必平行于α．平面必与α相交．平面必不垂直于α．存在△的一条中位线平行于α或在α内．设直线⊂平面α，过平面α外一点且与，α都成°角的直线有且只有() ．条．条．条．条解析：如图所示与α成°角的直线一定是以为顶点的圆锥的母线所在直线，当∠＝∠＝°时，直线，都满足条件，故选..下列命题中，正确的是()．经过不同的三点有且只有一个平面．分别在两个平面内的两条直线一定是异面直线．垂直于同一个平面的两条直线是平行直线．垂直于同一个平面的两个平面平行．用α表示一个平面，表示一条直线，则平面α内至少有一条直线与()．平行．相交．异面．垂直．若，表示直线，α表示平面，则下列命题中，正确的个数为()。

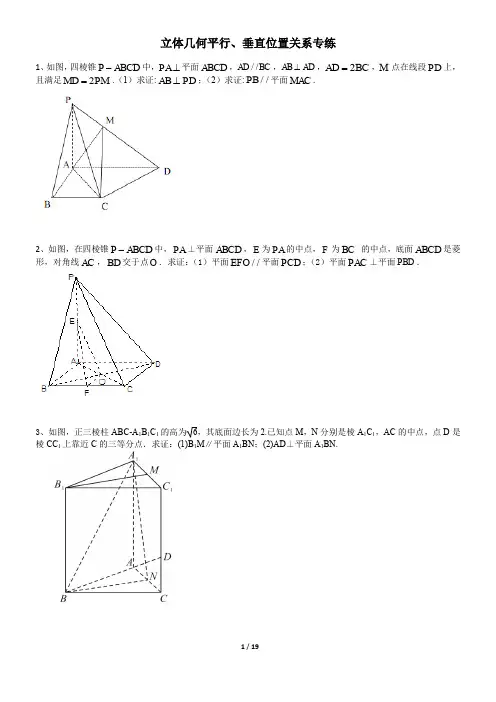
立体几何平行、垂直位置关系专练1、如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .2、如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ．3、如图，正三棱柱ABC-A 1B 1C 1的高为6，其底面边长为2.已知点M ，N 分别是棱A 1C 1，AC 的中点，点D 是棱CC 1上靠近C 的三等分点．求证：(1)B 1M ∥平面A 1BN ；(2)AD ⊥平面A 1BN.4、如图，等边三角形ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD＝2AE，AE⊥AB，M为AB的中点．(1)证明：CM⊥DE；(2)在边AC上找一点N，使CD∥平面BEN.5、如图，矩形ABCD所在平面与三角形ABE所在平面互相垂直，AE＝AB，M，N，H分别为DE，AB，BE 的中点．求证：(1)MN∥平面BEC；(2)AH⊥CE.6、如图，在三棱台ABCDEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE∩平面DEF＝a，求证：DF∥a；(2)若EF＝CF＝2BC，试问在线段BE上是否存在点G，使得平面DFG⊥平面CDE？若存在请确定点G的位置；若不存在，请说明理由．7、在三棱锥S ABC -中，平面SAB ⊥平面SBC ，AB BC ⊥，AS AB =，过A 作AF SB ⊥，垂足为F ，点E ，G 分别是棱SA ，SC 的中点．（1）求证：平面EFG ∥平面ABC ．（2）求证：BC SA ⊥．8、如图，在直三棱柱111ABC A B C -中，AB BC ⊥，点D 为棱1C C 的中点，1AC 与1A D 交于点E ，1BC 与1B D 交于点F ，连结EF .求证：（1）//AB EF ；（2）平面11A B D ⊥平面11B BCC .9、【2019年高考江苏卷】如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1；（2）BE ⊥C 1E ．点，平面PAB ⊥底面ABCD ，90PAB ∠= ．求证：（1）//PB 平面AEC ；（2）平面PAC ⊥平面ABCD ．11、2.（2020·江苏省镇江高三二模）如图，三棱锥P ABC -中，点D ，E 分别为AB ，BC 的中点，且平面PDE ⊥平面ABC ．()1求证：//AC 平面PDE ；()2若2PD AC ==，PE =PBC ⊥平面ABC .12、（2020·江苏省建湖高级中学高三月考）如图，在四面体ABCD 中，,90AD BD ABC =∠= ，点,E F 分别为棱,AB AC 上的点，点G 为棱AD 的中点，且平面//EFG 平面BCD ．（1）求证：12EF BC =；（2）求证：平面EFD ⊥平面ABC ．点，PA ⊥平面ABCD .（1）求证：//PB 平面AEC ；（2）若四边形ABCD 是矩形且PA AD =，求证：AE ⊥平面PCD .14、（2020·江苏省高三二模）如图，在三棱柱111ABC A B C -中，侧面11ABB A ⊥底面ABC ，AB AC ⊥，E ，F 分别是棱AB ，BC 的中点.求证：（1）11AC ∥平面1B EF ；（2）1AC B E ⊥.15、（2020·江苏省连云港高三）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，E 、F 分别为AD 、PB 的中点.（Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：//EF 平面PCD .16、（2020·江苏省苏州高三）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A1B 1∥平面DEC 1；（2）BE ⊥C 1E ．17、（2020·江苏省通州高三）如图，在三棱柱111ABC A B C -中，侧棱垂直于底面1,2,1,,AB BC AA AC BC E F ⊥===分别是11,AC BC 的中点．（1）求证: 平面ABE ⊥平面11B BCC ；（2）求证:1C F ∥平面ABE ；18、（2020·江苏省高三三模）如图，三棱柱111ABC A B C -中，1BC B C =，O 为四边形11ACC A 对角线交点，F 为棱1BB 的中点，且AF ⊥平面11BCC B .（1）证明：//OF 平面ABC ；（2）证明：四边形11ACC A 为矩形.参考答案1．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，//AD BC ，AB AD ⊥，2AD BC =，M 点在线段PD 上，且满足2MD PM =.（1）求证:AB PD ⊥；（2）求证://PB 平面MAC .【解析】（1）∵四棱锥P ABCD -中，PA ⊥平面ABCD ，AB 平面ABCD ， ∴AB PA ⊥，又AB AD ⊥，,PA AD ⊂平面PAD ，PA AD A ⋂=， ∴AB ⊥面PAD .PD ⊂面PAD ，∴AB PD ⊥. （2）连结BD AC O ⋂=，连结MO ， ∵//AD BC ，2AD BC =，2DO BO ∴=,∵在PBD ∆中，2DM MP =，2DO BO =∴//PB MO ， 又PB ⊄面MAC ，MO ⊂面MAC ，∴//PB 面MAC .2．如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，E 为PA 的中点，F 为BC 的中点，底面ABCD 是菱形，对角线AC ，BD 交于点O ．求证：（1）平面//EFO 平面PCD ；（2）平面PAC ⊥平面PBD ． 【详解】（1）因为在ΔPAC 中，E 为PA 的中点，O 为AC 的中点， 所以//EO PC又EO ⊄平面PCD ，PC ⊂平面PCD ， 所以//EO 平面PCD同理可证，//FO 平面PCD ，又EO FO O = ，EO ⊂平面EFO ,FO ⊂平面EFO 所以平面//EFO 平面PCD ．（2）因为PA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以PA BD ⊥因为底面ABCD 是菱形，所以AC BD ⊥，又,,PA AC A PA PAC AC PAC =⊂⊂ 平面平面所以BD ⊥平面PAC 。

人教版高一数学必修2空间直线的垂直关系练习题（含答案详解）必修 2 空间中的垂直关系基础知识点一、选择题：1. 若斜线段 AB 是它在平面α上的射影的长的 2倍，则 AB 与平面α所成的角是( ).2. 直线l ⊥平面α，直线m? α，则 ( ).A.l ⊥mB.l ∥mC.l ，m 异面D.l ， m 相交而不垂直3. 如图所示，PO ⊥平面 ABC ，BO ⊥AC ，在图中与 AC 垂直的线段有 ( ). 4. 若平面α⊥平面β，平面β⊥平面γ，则( ). C.30 °D.120C.3条 D.4 条A. α∥γ B. α⊥γ C. α与γ相交但不垂直D.以上都有可能5. 已知长方体 ABCD 1AB 1C 1D 1，在平面 AB 1上任取一点 M ，作ME ⊥AB 于 E ，则( ).A.ME ⊥平面 ACB.ME ? 平面 ACC.ME ∥平面 ACD. 以上都有A.1 条B.2可能6. 如图，设P是正方形ABCD外一点，且PA⊥平面ABCD，则平面PAB与平面PBC、平面PAD的位置关系是( ).A. 平面PAB与平面PBC、平面PAD都垂直B. 它们两两垂直C. 平面PAB与平面PBC垂直，与平面PAD不垂直D. 平面PAB与平面PBC、平面PAD都不垂直二、填空题：7. _________________________________ 在正方体A1B1C1D1ABCD 中，E，F分别是棱AB，BC的中点，O是底面ABCD的中心（如图），则EF与平面BB1O 的关系是 ______________________________ .8. 若a， b 表示直线，α表示平面，下列命题中正确的有___ 个.①a⊥α，b∥α? a⊥b; ②a⊥α，a⊥b? b∥α；③a∥α，a⊥b? b⊥α；④a⊥α，b⊥α? a∥b.9. α、β是两个不同的平面，m、n 是平面α及β外的两条不同的直线，给出四个论断：① m⊥n；②α⊥β；③m⊥α；④n⊥β. 以其中三个论断作为条件，余下的一个论断作为结论，写出你认为正确的一个命题 __ .10. 如图，正方体ABCD1AB1C1D1中，截面C1D1AB与底面ABCD所成二面角C1ABC的三、解答题：π11. 如图所示，在Rt△AOB中，∠ABO=6 ，斜边AB=4，Rt △AOC可以通过Rt △AOB 以直线AO为轴旋转得到，且二面角BAOC 是直二面角，D是AB的中点.求证：平面COD⊥平面AOB.12. 如图，在四棱锥P - ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=D，C E 是PC的中点，作EF⊥PB交PB于点F.(1) 求证：PA∥平面EDB；(2) 求证：PB⊥平面EFD.综合提高1. 已知l ，m，n 为两两垂直的三条异面直线，过l 作平面α与直线m垂直，则直线n 与平面α的关系是( ).A.n ∥αB.n ∥α或n? αC.n ? α或n 与α不平行D.n ? α2. 已知平面α⊥平面β，α∩β =l，点A∈α，A?l ，直线AB∥l ，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是( ).A.AB∥mB.AC ⊥mC.AB ∥βD.AC ⊥β3. 一个二面角的两个半平面分别垂直于另一个二面角的两个半平面，那么这两个二面角( ).A. 相等B. 互补C. 相等或互补D. 关系无法确定4. 如图，正方形SG1G2G3中，E，F分别是G1G2，G2G3的中点，现在沿SE，SF，EF 把这个正方形折成一个四面体，使G1、G2、G3 重合，重合后的点记为G.给出下列关系：①SG⊥平面EFG；②SE⊥平面EFG；③GF⊥ SE；④EF⊥平面SEG. 其中成立的有( ).A. ①②B. ①③C. ②③D. ③④5. 如果三棱锥的三个侧面两两相互垂直，则顶点在底面的正投影是底面三角形的心.6. 已知三棱柱ABCA1B1C1的侧棱与底面边长都相等，若A1在底面ABC内的射影为△ABC的中心，则AB1 与ABC底面所成的角的正弦值等于.7. 将正方形ABCD沿对角线BD折成直二面角ABDC，有如下四个结论：①AC⊥BD；②△ ACD是等边三角形；③ AB与平面BCD成60°的角；④ AB与CD 所成的角为60°.其中真命题的编号是 _____ ( 写出所有真命题的编号).8. 如图，A、B、C、D为空间四点，在△ ABC中，AB=2，AC=BC= 2，等边三角形ADB以AB为轴运动，当平面ADB⊥平面ABC时，则CD= .9. 如图所示，四边形ABCD为正方形，SA垂直于四边形ABCD 所在的平面，过点 A 且垂直于SC的平面分别交SB，SC，SD于点E，F，G.求证：AE⊥SB，AG⊥SD.10. 如图，在四棱锥P－ABCD中，PO⊥面ABCD，PD=DC=BC，=1AB=2，AB∥DC，∠ BCD=9°0 .(1) 求证：PC⊥BC.(2) 求点A到平面PBC的距离.11. 如图，已知平面PAB⊥平面ABC，平面PAC⊥平面ABC，AE⊥平面PBC，E 为垂足.(1) 求证：PA⊥平面ABC；(2) 当 E 为△ PBC的垂心时，求证：△ ABC是直角三角形.12. （创新拓展）已知△ BCD中，∠BCD=9°0 ，BC=CD=，1AB⊥平面BCD，∠ADB=60°，AE AFE，F 分别是AC，AD上的动点，且A AE C=A A F D=λ(0 <λ<1).(1) 求证：不论λ为何值，总有平面BEF⊥平面ABC；(2) 当λ为何值时，平面BEF⊥平面ACD?参考答案基础篇1. 答案A；解析斜线段、垂线段以及射影构成直角三角形. 如图所示，∠ABO OB1即是斜线AB与平面α所成的角，又AB=2BO，所以cos∠ABO=AB=2. 所以∠ ABO=60°. 故选 A.2. 答案A；解析无论l 与m是异面，还是相交，都有l ⊥m，考查线面垂直的定义，故选 A.3. 答案D；解析∵PO⊥平面ABC，∴ PO⊥AC，又∵ AC⊥BO，∴ AC⊥平面PBD，∴平面PBD中的4条线段PB，PD，PO，BD与AC垂直.4. 答案D；解析以正方体为模型：相邻两侧面都与底面垂直；相对的两侧面都与底面垂直；一侧面和一对角面都与底面垂直，故选 D.5. 答案A；解析由于ME? 平面AB1，平面AB1∩平面AC=AB，且平面AB1⊥平面AC，ME⊥AB，则ME⊥平面AC.6. 答案A；解析∵PA⊥平面ABCD，∴ PA⊥BC.又BC⊥AB，PA∩AB=A，∴BC⊥平面PAB，∵ BC? 平面PBC，∴平面PBC⊥平面PAB. 由AD⊥PA，AD⊥AB，PA∩AB=A，得AD⊥平面PAB.∵AD?。

北师大版高中数学必修第二册专题强化练9　空间中的垂直关系1.(2022河南南阳第一中学月考)设m,n,l是三条不同的直线,α,β是两个不同的平面,给出下列四个命题,其中正确的是( )A.若α⊥β,l⊂α,m⊂β,则l⊥mB.若α∥β,l⊂α,m⊂β,则l∥mA.37B.3+311C.6D.725.(多选题)如图,PA垂直于以AB为直径的圆所在的平面,点C是圆上异于A,B的任一点,则下列结论正确的是( )A.PC⊥BC B.AC⊥平面PCBC.D.面在四棱锥P-ABCD中,底面面答案与分层梯度式解析专题强化练9　空间中的垂直关系1.C　对于A,若α⊥β,l⊂α,m⊂β,则l与m可能平行、相交或异面,A不正确;对于B,若α∥β,l⊂α,m⊂β,则l与m可能平行或异面,B不正确;对于C,如图,过l作平面γ,γ∩β=l',∵l∥β,l⊂γ,γ∩β=l',∴l∥l',∵l⊥α,∴l'⊥α,又l'⊂β,∴α⊥β,C正确;对于D,当l⊂α,l⊥m,l⊥n,m∥β,n∥β时,α与β还可能平行或斜交,D不正确.故选C.2.D　∵平面PAC⊥平面PBC,AC⊥PC,AC⊂平面PAC,平面PAC∩平面PBC=PC,∴AC⊥平面PBC.∵BC⊂平面PBC,∴AC⊥BC,∴∠ACB=90°,∴动点C的运动轨迹是以AB为直径的圆(除去A,B两点).3.AC　对于A,由题意得PE⊥平面ABCD,连接AC,交BD于点H,若E与H不重合,则AH=CH,EH⊥AC,所以AE=EC,当E与H重合时,显然AE=EC,又PA=PE2+AE2,PC=PE2+CE2,所以PA=PC,A正确;对于B,PD=PE2+ED2,PB=PE2+EB2,由于ED与EB不一定相等,所以PB,PD不一定相等,B错误;对于C,因为PE⊥平面ABCD,AC⊂平面ABCD,所以PE⊥AC,又因为AC⊥BD,PE∩BD=E,PE,BD⊂平面PBD,所以AC⊥平面PBD,C正确;对于D,连接PH,若E,H不重合,则PH与EH不垂直,故BD与PH不垂直,则BD与平面PAC 不垂直,D错误.故选AC.4.A　连接A1B,根据题意,得△CC1B为直角三角形,因为∠ACB=90°,所以∠A1C1B1=90°,即A1C1⊥B1C1,因为AA1⊥底面A1B1C1,CC1∥AA1,所以CC1⊥底面A1B1C1,所以CC1⊥A1C1,又即则当且仅当C,P,A1三点共线B=30°,又在22即∵又∴BC⊥平面PAC,又PC⊂平面PAC,∴PC⊥BC,故A正确;∵BC⊂平面PBC,∴平面PBC⊥平面PAC,故D正确;若AC⊥平面PCB,则AC⊥PC,∵PA⊥平面ABC,∴PA⊥AC,与AC⊥PC矛盾,故B错误;过点C 作CD ⊥PB 于D,若平面PAB ⊥平面PBC,且平面PAB∩平面PBC=PB,CD ⊂平面PBC,则CD ⊥平面PAB,又PA ⊂平面PAB,∴CD ⊥PA,又PA ⊥BC,CD∩BC=C,CD,BC ⊂平面PBC,∴PA ⊥平面PBC,∵PC ⊂平面PBC,∴PA ⊥PC,与PA ⊥AC 矛盾,故C 错误.故选AD.6.答案　63解析　在Rt △ABC 中,BC=33,∠BAC=π6,AC ⊥BC,则AB=233,因为平面ABC ⊥平面α,平面ABC∩平面α=AC,AC ⊥BC,BC ⊂平面ABC,所以BC ⊥平面α,因为CP ⊂平面α,所以BC ⊥CP,则CP=BP 2-BC 2=BP 2-13(在Rt △BCP 中,CP 最短,即BP 最短),设∠ABP=θ(0<θ<π),则S △ABP =12AB·BPsin θ,即33=12×233BP·sin θ,得BP=1sinθ,当sin θ=1,即θ=π2,即AB ⊥BP 时,BP 的长度取得最小值1,此时CP 的长度取得最小值,为12-13=63.7.解析　(1)当a=2时,BD ⊥平面PAC.证明如下:当a=2时,矩形ABCD 为正方形,则BD ⊥AC.∵PA ⊥平面ABCD,BD ⊂平面ABCD,∴BD ⊥PA.又AC∩PA=A,AC,PA ⊂平面PAC,∴BD ⊥平面PAC.故当a=2时,BD ⊥平面PAC.(2)连接AM.∵PA ⊥平面ABCD,DM ⊂平面ABCD,∴DM ⊥PA,又PM ⊥DM,PA∩PM=P,PA,PM ⊂平面PAM,∴DM ⊥平面PAM,∵AM ⊂平面PAM,∴DM ⊥AM,∴点M 是以AD 为直径的圆和棱BC 的交点,∴圆的半径r=AD 2≥AB,即a≥4,∴a 的取值范围是[4,+∞).。

2022版人教A版高中数学必修第二册--专题强化练6空间中的垂直关系一、选择题1.(2020河北石家庄第二中学高一下月考,)已知正方体ABCD-A1B1C1D1的棱AA1的中点为E,AC与BD交于点O,平面α过点E且与直线OC1垂直,若AB=1,则平面α截该正方体所得截面图形的面积为()A.√64B.√62C.√32D.√342.(2020山东烟台第二中学高一下月考,)如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么在这个空间图形中必有()A.AG⊥平面EFHB.AH⊥平面EFHC.HF⊥平面AEFD.HG⊥平面AEF3.()在三棱柱ABC-A1B1C1中,已知AB⊥AC,AA1⊥平面A1B1C1,则下列选项中,能使异面直线BC1与A1C相互垂直的条件为()A.∠A1CA=45°B.∠BCA=45°C.四边形ABB1A1为正方形D.四边形BCC1B1为正方形二、填空题4.(2020安徽合肥一六八中学高二上期中,)经过平面α外一点和平面α内一点与平面α垂直的平面有个.5.(2021河南开封高一上期末,)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点P在正方体的表面上移动,且满足B1P⊥D1B,则满足条件的所有点P构成的平面图形的面积是.三、解答题6.(2021安徽合肥高二上期末联考,)如图,在三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.(1)求证:DM⊥平面BPC;(2)求证:平面ABC⊥平面APC;(3)若BC=4,AB=20,求三棱锥D-BCM的体积.7.(2020四川南充高三第一次适应性考试,)如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2,BC=a,PA⊥底面ABCD.(1)当a为何值时,BD⊥平面PAC?证明你的结论;(2)若在棱BC上至少存在一点M,使PM⊥DM,求a的取值范围.答案全解全析一、选择题1.A连接A1C1,OE,BE,ED,C1E.易得O C12=1+12=32,OE2=14+12=34,E C12=2+14=94,∴O C12+OE2=EC12,∴OE⊥OC1.易得BD⊥平面ACC1A1,∴BD⊥OC1.又OE∩BD=O,∴OC1⊥平面BDE,∴所得截面为△BDE.易知BD⊥OE,∴S△BDE=12BD·OE=12×√2×√32=√64,∴平面α截该正方体所得截面图形的面积为√64.故选A.2.B易知AH⊥HE,AH⊥HF,又HE∩HF=H,∴AH⊥平面EFH,∴B正确;∵过A只有一条直线与平面EFH垂直,∴A不正确;易知AG⊥EF,EF⊥AH,又AG∩AH=A,∴EF⊥平面HAG,又EF⊂平面AEF,∴平面HAG⊥平面AEF,过H作直线l垂直于平面AEF,则l一定在平面HAG内,∴C不正确;∵HG与AG不垂直,∴HG⊥平面AEF不正确,∴D不正确.故选B.3.A如图,连接AC1.易知AA1⊥平面ABC,∴AA1⊥AB,又AB⊥AC,AA1∩AC=A,∴AB⊥平面ACC1A1.∵A1C⊂平面ACC1A1,∴AB⊥A1C,当异面直线BC1与A1C相互垂直时,由AB∩BC1=B,可得A1C⊥平面ABC1,∵AC1⊂平面ABC1,∴A1C⊥AC1,∴四边形ACC1A1为正方形,∴∠A1CA=45°,反之亦然,即∠A1CA=45°时,可得BC1⊥A1C成立.故选A.二、填空题4.答案1或无数解析设平面α外一点为A,平面α内一点为O.若OA⊥α,则过OA的任一平面都与平面α垂直,所以过OA存在无数个平面与平面α垂直;若OA不垂直于α,则过点A有唯一的直线l与平面α垂直,OA与l确定唯一的平面与α垂直,所以过OA存在唯一的平面与平面α垂直.5.答案2√3解析连接AC,B1C,AB1,BD,BC1(图略).在正方体ABCD-A1B1C1D1中,易知AC⊥DD1,AC⊥BD,B1C⊥BC1,B1C⊥C1D1.∵BD∩DD1=D,∴AC⊥平面BDD1,又BD1⊂平面BDD1,∴AC⊥BD1.同理B1C⊥BD1,又AC∩B1C=C,∴BD1⊥平面AB1C.∴满足条件的点P构成的图形为△AB1C.由正方体的棱长为2,可知△AB1C是边长为2√2的等边三角形.∴点P构成的平面图形的面积S△AB1C =√34×(2√2)2=2√3.三、解答题6.解析(1)证明:由题可知DM是△APB的中位线,∴DM∥AP,又∵AP⊥PC,∴DM ⊥PC,∵△PMB为正三角形,D为PB的中点,∴DM⊥PB,又∵PB⊂平面BPC,PC⊂平面BPC,PB∩PC=P,∴DM⊥平面BPC.(2)证明:∵DM⊥平面BPC,DM∥AP,∴AP⊥平面BPC,∵BC⊂平面BPC,∴AP⊥BC.又∵AC⊥BC,AP⊂平面APC,AC⊂平面APC,AP∩AC=A,∴BC⊥平面APC,∵BC⊂平面ABC,∴平面ABC⊥平面APC.(3)∵AB=20,∴PB=BM=12AB=10,∴DM=5√3,∴AP=2DM=10√3,∵BC=4,∴AC=√AB2-BC2=8√6,∴PC=√AC2-AP2=2√21.∵PC2+BC2=PB2,∴PC⊥BC.∴S△PBC=12BC·PC=4√21,∴S△BCD=12S△PBC=2√21.∴三棱锥D-BCM的体积V=13S△BCD·DM=13×2√21×5√3=10√7.7.解析(1)当a=2时,BD⊥平面PAC.证明如下:当a=2时,矩形ABCD为正方形,则BD⊥AC.∵PA⊥平面ABCD,BD⊂平面ABCD,∴BD⊥PA.又AC∩PA=A,AC⊂平面PAC,PA⊂平面PAC,∴BD⊥平面PAC.故当a=2时,BD⊥平面PAC.(2)设M是符合条件的棱BC上的点.连接AM.∵PA⊥平面ABCD,DM⊂平面ABCD,∴DM⊥PA,又PM⊥DM,PA∩PM=P,PA⊂平面PAM,PM⊂平面PAM,∴DM⊥平面PAM,∵AM⊂平面PAM,∴DM⊥AM,∴点M是以AD为直径的圆和BC的交点,≥AB,即a≥4,∴半径r=AD2∴a的取值范围是[4,+∞).。

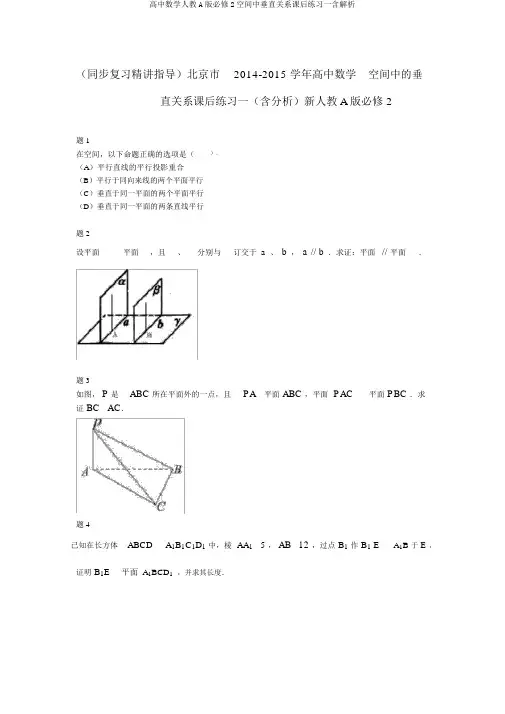
（同步复习精讲指导）北京市2014-2015 学年高中数学空间中的垂直关系课后练习一（含分析）新人教A版必修 2题1）．在空间，以下命题正确的选项是（（A）平行直线的平行投影重合（B）平行于同向来线的两个平面平行（C）垂直于同一平面的两个平面平行（D）垂直于同一平面的两条直线平行题2设平面平面，且、分别与订交于a、b，a // b．求证：平面// 平面．题3如图， P是ABC 所在平面外的一点，且PA 平面 ABC ，平面 PAC平面 PBC ．求证 BC AC．题4已知在长方体ABCD A1B1C1D1中，棱 AA1 5 ，AB12 ，过点B1作B1E A1B 于E，证明 B1E平面A1BCD1，并求其长度．题5在正方体 ABCD A1B1C1D1中，E是 BB1的中点，O是底面正方形ABCD 的中心．求证： OE平面ACD1．题6如图，圆柱的轴截面ABCD 是正方形，点 E 在底面圆周上， AF DE ， F 是垂足，求证：AF DB ．题7如下图， P是四边形 ABCD所在平面外的一点， ABCD是∠ DAB＝60°且边长为 a的菱形．侧面PAD为正三角形，其所在平面垂直于底面 ABCD．(1)若 G为 AD边的中点，求证： BG⊥平面 PAD；(2)求证： AD⊥ PB．题8已知在四棱锥 P- ABCD中，底面 ABCD是边长为4的正方形，△ PAD是正三角形，平面 PAD⊥平面 ABCD， E、 F、 G分别是 PD、 PC、 BC的中点．（I ）求证：PA// 平面EFG；（II ）求平面EFG 平面 PAD．题9如图，在长方形 ABCD中， AB＝2，BC＝1，E为 DC的中点， F为线段 EC(端点除外)上一动点．现将△ AFD沿 AF折起，使平面 ABD⊥平面 ABC．在平面 ABD内过点 D作DK⊥ AB，K为垂足．设AK＝ t ，则t 的取值范围是__________．题10如图， BC是Rt△ ABC的斜边， AP⊥平面 ABC，PD⊥ BC于 D点，则图中共有直角三角形的个数是() ．A．8B．7C．6D．5课后练习详解题1答案： D．详解：由空间直线与平面的地点关系及线面垂直与平行的判断与性质定理能够很简单得出答案．平行直线的平行投影重合，还可能平行， A 错误；平行于同向来线的两个平面平行，两个平面可能订交，B错误；垂直于同一平面的两个平面平行，可能订交， C 错误．题2答案：见详解．证明：在平面内作直线 a 的垂线 l1，垂足为A，由于，平面平面，平面I 平面=a，因此l1在平面内作直线 b 的垂线l2，垂足为 B ，同理可证得l2l1 // l 2，又 Q l1,l 2， l1 //Q a // b a,b， a //Q l1 I a A, l1, a//题3答案：见详解．详解：在平面PAC 内作 AD PC，交 PC于D．由于平面 PAC平面 PBC 于 PC， AD平面 PAC ，且 AD PC ，因此 AD平面 PBC ．又由于于是有BC 平面 PBC ，AD BC ①．此外因此PA 平面 ABC ， BC平面ABC，PA BC ②．由①②及 AD PA A ，可知由于因此题4BC 平面 PAC ．AC 平面 PAC ，BC AC ．答案： B1E 60 13详解：∵ BC平面 A1 ABB1，且 B1 E平面 AA1 B1 B ，∴ BC B1 E ，又 B1E A1B ，又 BC A1B B ，∴ B1E平面 A1BCD1．A 1B 1 BB 15 1260，∴ BE60 在 Rt A 1 B 1 B 中， B 1 E．A 1 B52 12 2 13 113题5证明 : 连结 AE 、CE ， D 1O ，设正方体 DB 1 的棱长为 a ，易证 AE CE ．又∵ AO OC ，∴ OE AC ．在正方体 DB 1中易求出：2D 1ODD 12DO2a22 a6a ，2222OEBE2OB2a2 a3a ，222D 1 ED 1B 12B 1E22a23a ．2a22∵ D 1O 2 OE 2 D 1E 2 ，∴ D 1O OE ．∵ D 1O ACO ，D 1O 、AC平面 ACD 1 ，∴ OE平面 ACD 1 ．题6答案：见详解．详解：由 DA底面 ABE ，知 DABE ；又 E 为底面圆周上一点， AB 为底面圆直径，知 BE AE ，故 BE 平面 ADE ，则 BE AF ，又 AF DE ，则 AF 平面 BDE ，则 AF DB ．题7答案：见详解．详解： (1) 连结 PG ，由题知△ PAD 为正三角形， G 是 AD 的中点，∴ PG ⊥AD ． 又平面 PAD ⊥平面 ABCD ，∴PG ⊥平面 ABCD ，∴ PG ⊥BG ．又∵四边形 ABCD 是菱形且∠ DAB ＝60°， ∴△ ABD 是正三角形，∴ B G ⊥AD ． 又AD ∩ PG ＝G ，∴ BG ⊥平面 PAD ．(2) 由 (1) 可知 BG ⊥ AD ， PG ⊥ AD ．因此 AD ⊥平面 PBG ，因此 AD ⊥PB ．题8答案：见详解．详解：证明：（ I ）取AD的中点H，连结EH，HG．∵H， G为 AD， BC的中点，∴ HG// CD，又 EF// CD．∴ EF// HG，∴ E，F， G，H四点共面，又∵PA//EH，EH 平面EFGH，PA 平面EFGH，∴PA//平面 EFG．（II ）证明：AD CD, PD CD ，∴ CD 平面PAD，∵EF// CD，∴EF平面 PAD，∵EF 平面EFG，∴平面EFG平面PAD．题91答案： ( 2，1)详解：过 K 作 KM⊥ AF于 M点，连结 DM，易得 DM⊥ AF，与折前的图形对照，可知由折前的图形中 D、M、 K 三点共线且DK⊥ AF，于是△ DAK∽△ FDA，∴AK AD t11＝，又＝，∴ t ＝．又AD DF1DF DF1DF∈(1,2)，∴ t ∈(2，1) ．题10答案： A．详解：所给图形中的△ PAC、△ PAD、△ PAB、△ PCD、△ PBD、△ ACD、△ ADB、△ ABC 均为直角三角形，因此共有 8 个直角三角形．。

人教版高中数学必修第二册空间中的平行关系课后练习1.下列选项中，一定能得出直线m 与平面α平行的是()A．直线m 在平面α外B．直线m 与平面α内的两条直线平行C．平面α外的直线m 与平面内的一条直线平行D．直线m 与平面α内的一条直线平行2.若一个平面内的两条直线分别平行于另一个平面内的两条直线，则这两个平面的位置关系是()A．一定平行B．一定相交C．平行或相交D．以上判断都不对3.梯形ABCD 中，AB ∥CD ，AB ⊂平面α，CD ⊄平面α，则直线CD 与平面α内的直线的位置关系只能是()A．平行B．平行或异面C．平行或相交D．异面或相交4.在正方体ABCD －A 1B 1C 1D 1中，M 是棱CD 上的动点，则直线MC 1与平面AA 1B 1B 的位置关系是()A．相交B．平行C．异面D．相交或平行5.①若直线a 在平面α外，则a ∥α；②若直线a ∥b ，直线b ⊂α，则a ∥α；③若直线a ∥b ，b ⊂α，那么直线a 就平行于平面α内的无数条直线．其中正确说法的个数为()A．0B．1C．2D．36.已知l ，m 是两条直线，α是平面，若要得到“l ∥α”，则需要在条件“m ⊂α，l ∥m ”中另外添加的一个条件是________．7.平面α∥平面β，直线l ∥α，则直线l 与平面β的位置关系是________．8.已知平面α，β和直线a ，b ，c ，且a ∥b ∥c ，a ⊂α，b ，c ⊂β，则α与β的关系是________．9.设a ，b 是不同的直线，α，β是两个不同的平面，给出下列结论：①若a ∥α，b ∥β，α∥β，则a ∥b ；②若α∥β，a ∥α，a ⊄β，则a ∥β；③若α∥β，A ∈α，过点A 作直线l ∥β，则l ⊂α；④平行于同一个平面的两个平面平行．其中所有正确结论的序号是________．10.如图所示，已知P 是平行四边形ABCD 所在平面外一点，M 为PB 的中点．求证：PD ∥平面MAC .11.如图所示，在正方体ABCD ﹣A 1B 1C 1D 1中，E 、F 、G 、H 、分别是BC 、CC 1、C 1D 1、A 1A 的中点，求证：（1）EG ∥平面BB 1D 1D ；（2）平面BDF ∥平面B 1D 1H ．12.已知如图，斜三棱柱ABC ﹣A 1B 1C 1中，点D 、D 1分别为AC 、A 1C 1上的点．（1）当等于何值时，BC 1∥平面AB 1D 1？（2）若平面BC 1D ∥平面AB 1D 1，求的值．答案1.C2.C3.B4.B5.B6.α⊄l7.ββ⊂l l 或//8.相交或平行9.②③④．10.证明:如图所示，连接BD 交AC 于点O ，连接MO ，则MO 为△BDP 的中位线，∴PD ∥MO .∵PD ⊄平面MAC ，MO ⊂平面MAC ，∴PD ∥平面MAC .11.证明：（Ⅰ）取BD 中点O ．连接OE ，OD1，则OE DC ，∴OE ∥D 1G∴四边形OEGD 1是平行四边形∴GE ∥D 1O ，又D 1O ⊂平面BDD 1B 1，且EG ⊄平面BDD 1B 1，∴EG ∥平面BDD 1B 1，（4分）（Ⅱ）取BB 1中点M ，连接HM 、C 1M ，则HM ∥AB ∥C 1D 1，∴HMC 1D 1是平行四边形，∴HD 1∥MC 1，又MC 1∥BF ，∴BF ∥HD 1，又BD ∥B 1D 1，B 1D 1，HD 1⊂平面HB 1D 1，BF ，BD ⊂平面BDF ，且B 1D 1∩HD 1＝D 1，BD ∩BF ＝B ，∴平面BDF ∥平面HB 1D 1．（8分）12.解：（1）如图，取D 1为线段A 1C 1的中点，此时＝1，连接A 1B 交AB 1于点O ，连接OD 1．由棱柱的性质，知四边形A 1ABB 1为平行四边形，所以点O 为A 1B 的中点．在△A 1BC 1中，点O 、D 1分别为A 1B 、A 1C 1的中点，∴OD 1∥BC 1．又∵OD 1⊂平面AB 1D 1，BC 1⊄平面AB 1D 1，∴BC 1∥平面AB 1D 1．∴＝1时，BC 1∥平面AB 1D 1，（2）由已知，平面BC 1D ∥平面AB 1D 1且平面A 1BC 1∩平面BDC 1＝BC 1，平面A 1BC 1∩平面AB 1D 1＝D 1O ．因此BC 1∥D 1O ，同理AD 1∥DC 1．∴＝，＝．又∵＝1，∴＝1，即＝1．。

课后导练基础达标1直线l 1的倾斜角为30°,直线l 2⊥l 1,则直线l 2的斜率为( ) A.3 B.3- C.33 D.33- 解析：设l 1的斜率为k 1,则k 1=tan30°=33,设l 2的斜率为k 2,∵l 1⊥l 2,∴k 1k 2=-1.∴k 2=3-. 答案：B2若l 1与l 2为两条不重合的直线,它们的倾斜角分别是α1,α2,斜率分别为k 1,k 2,则下列命题,其中正确命题的个数是( )①若l 1∥l 2,则斜率k 1=k 2 ②若k 1=k 2,则l 1∥l 2 ③若l 1∥l 2,则倾斜角α1=α2 ④若α1=α2,则l 1∥l 2A.1B.2C.3D.4解析：由两线平行的判定方法可知,①②③④都正确.答案：D3已知过点A(-2,m)和B(m,4)的直线与斜率为-2的直线平行,则m 的值( )A.-8B.0C.2D.10解析：k AB =24+-m m ,由24+-m m =-2,得m=-8. 答案：A4直线l 过点(a,b)和(b,a),其中a≠b ,则( )A.l 与x 轴垂直B.l 与y 轴垂直C.l 过一、二、三象限D.l 的倾角为135°解析：设直线l 的斜率为k,倾斜角为α.则k=tanα=ab b a --=-1,∴α=135°. 答案：D5若直线l 1∥l 2,且l 1的倾斜角为45°,l 2过点(4,6),则l 2还过下列各点中的( )A.(1,8)B.(-2,0)C.(9,2)D.(0,-8)解析：∵k 1=tan45°,又l 1∥l 2.∴k 2=1.设过点(x,y),则46--x y =1. 即y=x+2,代入检验可知选B.答案：B6原点在直线l 上的射影是P(-2,1),则l 的斜率为_______.解析：设l 的斜率为k,由条件知k OP =21-,又知l ⊥OP, ∴21-k=-1.∴k=2. 答案：27已知点P(3,m)在过M(2,-1)和N(-3,4)的直线上,则m 的值是____________.解析：因为P,M,N 三点共线,所以k PM =k MN .即3241231+--=-+m .得m=-2. 答案：-28顺次连结A(-4,3),B(2,5),C(6,3),D(-3,0),所组成的图形ABCD 是什么图形？解析：如图.∵k AB =314235=+-k BC =216235-=--, k CD =313603=+-, k DA =3403+--=-3. 则k AB =k CD .∴AB ∥CD.k AB ·k DA =-1.∴AD ⊥AB,同理AD ⊥DC.又k BC ≠k AD .∴AD 与BC 不平行.故四边形ABCD 是直角梯形.综合运用9过点(6,3),(0,3)的直线与过点(2,6),(2,0)的直线的位置关系为( )A.相交不垂直B.垂直C.平行D.重合解析：由条件知k 1=320336-=--, k 2=2312602-=--. ∴k 1·k 2=-1.答案：B10已知直线l 1的斜率为3,直线l 2经过点A(1,2),B(2,a),若l 1∥l 2,则a 的值为________;若l 1⊥l 2,则a 的值为____________.解析：k 1=3.k 2=a-2,若l 1∥l 2,则k 1=k 2.即a-2=3.∴a=5,若l 1⊥l 2,则k 1·k 2=-1.即3(a-2)=-1.得a=35. 答案：5 5/311已知△ABC 的顶点B(2,1),C(-6,3),其垂心为H(-3,2),求顶点A 的坐标.解：设A(a,b),∵H 为△ABC 的垂心,∴AH ⊥BC,BH ⊥AC.又知k AH =32+-a b ,k BC =41-,k BH =51-,k AC =63+-a b , 由⎩⎨⎧-=-⎪⎪⎩⎪⎪⎨⎧-=-∙+--=-∙+-.62,19.1)51(63,1)41(32b a a b a b 解得 ∴A 的坐标为(-19,-62).拓展探究12已知A(0,3),B(-1,0),C(3,0),求点D 的坐标,使四边形ABCD 为直角梯形(A 、B 、C 、D 按逆时针方向排列).解：如图,设D(a,b),(1)当AB ∥CD,且∠BAD=90°时,∵k AD =a b 3-,k AB =3,k CD =3-a b .由于AD ⊥AB.且AB ∥CD. ∴⎪⎪⎩⎪⎪⎨⎧==⎪⎪⎩⎪⎪⎨⎧=--=∙-.59,518,33,133b a a b a b 解得 此时AD 与BC 不平行.(2)当AD ∥BC 且∠ACD=90°时,此时D(3,3),此时AB 与CD 不平行.故点D 的坐标为(3,3)和(59,518).。