当前位置：文档之家 › 复变函数第三讲解析函数的充要条件初等函数

复变函数第三讲解析函数的充要条件初等函数

  • 格式：ppt
  • 大小：565.50 KB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

解析函数的充要条件

解析函数的充要条件


那么在曲线的交点处，i)uy、 vy 均不为零时， 那么在曲线的交点处， 、 均不为零时， 由隐函数求导法则知曲线族 u(x, y)=C1， v(x, y)=C2中任一条曲线的斜率分别为
k1 = − u x / u y
k2 = −v x / v y
利用C-R方程 ux=vy, uy=-vx 有 方程 利用 k1k2=(-ux/uy)(-vx/vy)= -1，即：两族曲线互相正交 两族曲线互相正交. ，
∂u ∂v = ∂x ∂y
上述条件满足时,有 上述条件满足时 有
∂v ∂u =− ∂x ∂y
f ' ( z ) = ux + iv x = ux − iu y = v y − iu y = v y + iv x
证明 " ⇒ " 方程满足上面已证！ （由f (z)的可导⇒ C-R方程满足上面已证！只须证 的可导 方程满足上面已证 f (z)的可导 ⇒ 函数 u(x, y)、v(x, y)可微）。 的可导 、 可微 可导， ∵函数 w =f (z)点 z可导，即 点 可导
定理2 函数f 定理 函数 (z)=u(x, y)+iv(x, y)在D内解析充要 在 内解析充要 条件是 u(x, y) 和 v(x, y)在D内可微，且 在 内可微， 满足Cauchy-Riemann方程 方程 满足
∂u ∂v = ∂x ∂y ∂v ∂u =− ∂x ∂y
֠
由此可以看出可导函数的实部与虚部有密切 的联系.当一个函数可导时, 的联系.当一个函数可导时,仅由其实部或虚部就可 以求出导数来. 以求出导数来.
例3 若 f ' ( z ) ≡ 0 , z ∈ D ⇒ f ( z ) = C , z ∈ D
复变函数第二章 第3节：初等函数

复变函数第二章 第3节：初等函数

sin( z) cos z;
2
cos( z) cos z;
其它三角函数：
eiz eiz
cos z
;
2
tan z sin z , cos z
eiz eiz
sin z
;
2i
cot z cos z , sin z
sec z 1 , cos z
csc z 1 , sin z
除分母为零的点外处处解析，且
双曲正弦
双曲正切
thz
shz chz
ez ez
ez ez
.
4、双曲函数的性质
chz ez ez , 2
shz ez ez . 2
(1) chz,shz 以2k i(k Z )为周期;
(2) chz 为偶函数, shz 为奇函数; (3) chz,shz 在复平面上处处解析，且
(shz) chz, (chz) shz,
ln z ln z i arg z.
Ln z ln z iArg z ln z i(arg z 2k ), Ln z ln z 2ki, k Z
当k=0时, Ln z 取到主值 ln z
特别，如 z= x>0, 则：
ln z ln z i arg z ln x,
但 Ln z ln x 2ki, k Z
1、三角函数的定义 cos y eiy eiy , 2
sin y eiy eiy . 2i
eiz eiz
cos z
;
sin z eiz eiz ;
2
2i
余弦函数
正弦函数
Euler公式的复数形式： eiz cos z i sin z
2、三角函数的性质
eiz eiz
第三讲 复变函数 解析函数1

第三讲 复变函数 解析函数1


§2.1 解析函数的概念
1. 复变函数的导数定义 2. 解析函数的概念
一、解析函数的概念
1 复变函数的导数 定义：
函数w = f ( z ), z ∈ D; z 0 , z 0 + ∆z ∈ D
f ( z 0 + ∆z ) − f ( z 0 ) ∆w lim 若极限 lim = ∆z →0 ∆z → 0 ∆ z ∆z
f ( z ) ' f ' ( z ) g ( z ) − f ( z ) g' ( z ) , ( g ( z ) ≠ 0) g( z ) = 2 g (z)
由以上讨论 ⇒ P ( z ) = a 0 + a1 z + ⋯ + a n z n 在整个复平面上处处可 导； P(z) R( z ) = 在复平面上（ 点外） 在复平面上（除分母为 0点外）处 Q( z ) 处可导 .
(3)有界闭区域D上的连续函数必有界，且其模 在D上取到最大值与最小值;
例题2 讨论
f (z) = arg z
π
2
的连续性。
argz在区域 −π < argz < π内连续，
π
2
−π
−
π
θ
0 0
x
在负实轴 argz = π上不连续。
π
2
−
π
2
第二章 解析函数
第一节 第二节 第三节 解析函数的概念 函数解析的充要条件 初等函数
例2 问 f (z) = x +2yi 是否可导?
f (z +∆z) − f (z) [解] 这里 lim ∆z→0 ∆z ( x + ∆x) + 2( y + ∆y )i − x − 2 yi ∆x + 2∆yi = lim = lim ∆z →0 ∆z → 0 ∆x + ∆yi ∆x + ∆yi ∆x + 2∆yi ∆x = lim = 1. 取∆z = ∆x → 0 , lim ∆z→0 ∆ + ∆ x yi ∆z→0 ∆x ∆x + 2∆yi 2∆y 取∆z = i∆y → 0, lim = lim = 2. ∆z→0 ∆ + ∆ x yi ∆z→0 ∆y 所以 f (z) = x + 2yi 的导数不存在.
复变函数第三讲解析函数的充要条件初等函数

复变函数第三讲解析函数的充要条件初等函数

第三讲 解析函数的充要条件 初等函数
§2.2 解析函数的充要条件

1. 解析函数的充要条件

2. 举例
如果复变函数 w = f (z) = u(x, y) + iv(x, y)在定 义域 D内处处可导，则函数 w = f (z) 在 D内解析。 问题 如何判断函数的解析性呢？
本节从函数 u (x , y) 及 v (x , y) 的可导性，探求 函数w = f (z) 的可导性，从而给出判别函数解析的 一个充分必要条件，并给出解析函数的求导方法。
问常数 a ,b ,c ,d取何值时 , f(z ) 在复平面内处处解 ?
a=2 , b=-1 , c=-1 , d=2
§2.3 初等函数

1. 指数函数
2. 三角函数和双曲函数 3. 对数函数 4. 乘幂与幂函数 5. 反三角函数与反双曲函数
内 容 简 介
本节将实变函数的一些常用的初等函数 推广到复变函数情形，研究这些初等函数的 性质，并说明它的解析性。
1 u v v u i i y y y y
f ' ( z ) 存在 u v v u i i x x y y u v x y
定义 方程

u x v x
记忆
v u x y
u y v y
(2)∵ f (z)=ex(cosy +isiny) 则 u=excosy, v= exsiny
u u u v x x e cosy e siny x y x y v v v u x x e siny e cosy x y x y
u v x x f ' ( z ) i e cos y ie sin y f ( z ) x x
02-2.3解析函数的充要条件教学课件

02-2.3解析函数的充要条件教学课件


注：函数������ ������ = ������ ������, ������ + ������������ ������, ������ 在一点可导的一个充分条件：
(1) ������(������, ������), ������(������, ������)在一点具有一阶连续偏导数；
2
������
⇒
������(������
+
∆������) Δ������
−
������(������)
=
������������ ������������
+
������
������������ ������������
+
������1(
∆������
)
+ ������������2( ∆������
∆������
������������ ������������
������������
������������
Δ������ = ������������ Δ������ + ������������ Δ������ + ������1( ∆������ )； Δ������ = ������������ Δ������ + ������������ Δ������ + ������2( ∆������ )
������(������+Δ������)−������(������) − ������′(������) < ������
������
成立
其中 lim ������ (Δ������) = 0，������(������ + Δ������) − ������(������) = ������′(������)Δ������ + ������(Δ������)Δ������
【复变函数】第二章 解析函数(工科2版)

【复变函数】第二章 解析函数(工科2版)

(1) f ( z ) = | z |2
2 2 2 解: f ( z ) = | z | = x + y
∴ u( x , y ) = x 2 + y 2 , v ( x , y ) = 0
∂u ∂u ∂v ∂v = 2 x, = 2 y, = 0, =0 ∂x ∂y ∂x ∂y
条件, 由C-R条件 x=0, y=0 , 条件 所以在z=0处可导 处处不解析. 所以在 处可导, 处处不解析 处可导
目录
上页
下页
返回
结束
【例3】讨论下列函数的解析性 可导性 . 】讨论下列函数的解析性, (1). f ( z ) = x + 2 yi 在复平面上处处不可导, 解：f (z) 在复平面上处处不可导,处处不解析
( 2 ). f ( z ) = z 2
在复平面上处处可导, 解：f (z) 在复平面上处处可导,处处解析 1 ( 3 ). f ( z ) = z 1 解：f ′( z ) = − 2 除 z = 0 外处处可导,处处解析. 外处处可导,处处解析. z 1+ z ( 4 ). f ( z ) = 1− z 2 解：f ′( z ) = 外处处可导,处处解析. 2 除 z = 1 外处处可导,处处解析. (1 − z )
返回 结束
目录
上页
下页
内处处为0, 内为一个常数. 【例6】若f'(x)在D内处处为 则f(x)在D内为一个常数 】 在 内处处为 在 内为一个常数 Proof: 由导数的计算公式
∂u ∂v ∂u ∂v f ′( z ) = +i =0 ⇔ = 0, = 0, ∂x ∂x ∂x ∂x
∂u ∂v ∂v ∂u = 0, = 0, f ′( z ) = −i =0 ⇔ ∂y ∂y ∂y ∂y
第二章3解析函数的充要条件

第二章3解析函数的充要条件

Δ→0
设( + Δ) − () = Δ + Δ， ′ = + ,
(Δ) = 1 + 2
所以Δ + Δ = ( + )(Δ + Δ) + (1 + 2 )(Δ + Δ)
= Δ − Δ + 1 Δ − 2 Δ
+(Δ + Δ + 2 Δ + 1 Δ)

=

−

= −.
充分性
由于 + Δ −
= ( + Δ, + Δ) − (, ) + [( + Δ, + Δ) − (, )]
= Δ + Δ
由(, ), (, )在点(, )可微，可知




Δ =
Δ +


( + ∆) − ()
1 ( ∆ ) + 2 ( ∆ )
⇒
=
+
+
Δ


∆
′ ()

( + ∆) − ()
=
+
= lim
∆→0


Δ
即 在 = + 处可导.
注：函数 = , + , 在一点可导的一个充分条件：


=− .


证明：必要性
( + Δ) − ()
()在 = + 处可导， ⇒ () = lim
存在
Δ→0
Δ
∀ > 0, ∃ > 0, 当0 < Δ < 时，有
复变函数2-3初等函数

复变函数2-3初等函数


1 n
1 n Lnz 1 1 1 z n z e zn . n 1 b (3) 幂函数 w z ( 除去 b n 与 两种情况外) n 也是一个多值函数 , 当b 为无理数或复数时, 是无穷多值的.
Ln z 的主值
其余各值为 Lnz ln z 2ki ( k 1,2,),
对于每一个固定的 k , 上式确定一个单值函数 , 称为 Ln z 的一个分支.
特殊地,
当 z x 0 时, Ln z 的主值 ln z ln x ,
是实变数对数函数.
此时Lnx ln x 2ki ( x 0, k 1,2,),
3
一、指数函数
( e x )' e x 处处可导 实变：
1.指数函数的定义:
当函数 f ( z ) 在复平面内满足以下三 个条件:
(1) f ( z )在复平面内处处解析;
(2) f ( z ) f ( z );
(3)当Im( z ) 0时, f ( z ) e x , 其中x Re( z ).
有关正弦函数和余弦函数的几组重要公式
cos( z1 z2 ) cos z1 cos z2 sin z1 sin z2 , (1) sin( z1 z2 ) sin z1 cos z2 cos z1 sin z2 , 2 2 sin z cos z 1.
cos( x yi ) cos x cos yi sin x sin yi , ( 2) sin( x yi ) sin x cos yi cos x sin yi .
x x0 y 0
lim arg z
x x0 y 0
复变函数第二章(第三讲)

复变函数第二章(第三讲)


∂u ∂v 1 ∂u ∂v iii) 求导数： f '(z) = ∂x + i ∂x = i ∂y + ∂y 求导数：
前面我们常把复变函数看成是两个实函数拼成的, 前面我们常把复变函数看成是两个实函数拼成的, 但是求复变函数的导数时要注意, 但是求复变函数的导数时要注意, 并不是两个实函 数分别关于x, 求导简单拼凑成的 求导简单拼凑成的. 数分别关于 ,y求导简单拼凑成的.实可微与复可微 是完全不同的概念。 是完全不同的概念。
§2.2 解析函数的充要条件
Cauchy-Riemann定理 1. Cauchy-Riemann定理 2. 举例
Cauchy-Riemann定理 1. Cauchy-Riemann定理
定理 设f (z)= u + i v, z= x +i y, z0=x0+i y0, 则f (z)在 在
(1) u( x, y), v( x, y)在( x0 , y0 )可微, ∂u ∂v ∂u ∂v z0处可导⇔ . (2) = , = − 在( x0 , y0 )成立 ∂x ∂y ∂y ∂x 定义 方程
∂u ∂v = ∂x ∂y
∂v ∂u =− ∂x ∂y
称为Cauchy-Riemann方程(简称C-R方程).
֠
由此可以看出可导函数的实部与虚部有密切 的联系. 的联系.
֠ 利用该定理可以判断那些函数是不可导的. 利用该定理可以判断那些函数是不可导的.
基本步骤: 偏导数的连续性， 基本步骤 i) 判别 u(x, y)，v (x, y) 偏导数的连续性， ， ii) 验证 验证C-R条件 条件. 条件
由以上讨论得 函数； P ( z ) = a 0 + a1 z + L + a n z n 是整个复平面上的解析 函数； P(z) R( z ) = 是复平面上 ( 除分母为 0点外 )的解析函数 . Q( z)
复变三-初等函数

复变三-初等函数


sin( z 2 ) sin z , cos( z 2 ) cos z . 同样, shz , chz 都是以 2i 为周期的周期函数. (3) 正弦函数和余弦函数在复平面内都是解析函数. (sin z ) cos z , (cos z ) sin z . iz iz iz iz e e e e 事实上， (sin z ) ( ) cos z 2i 2 同理 ( shz ) chz, (chz ) shz
9
一些常用的重要公式：
cos(z1 z2 ) cos z1 cos z2 sin z1 sin z2 , (1) sin(z1 z2 ) sin z1 cos z2 cos z1 sin z2 , 2 2 sin z cos z 1.
cos( x yi ) cos x cos yi sin x sin yi , ( 2) sin( x yi ) sin x cos yi cos x sin yi .
sin xchy i cos xshy cos xchy i sin xshy sin x cos x ichyshy cos 2 xch2 y (1 cos 2 x ) sh2 y sin 2 x sh2 y 2 2 i 2 2 . 2 cos x 2 sh y 2 cos x 2 sh y Re(tan z ) Im(tan z )
19
例 6 求下列各式的值: (1) Ln( 2 3i ); (2) Ln(3 3i ).
解 (1) Ln( 2 3i )
ln 2 3i iArg( 2 3i )
1 3 ln 13 i arctan 2k . 2 2
(最新整理)(完整版)复变函数解析函数

(最新整理)(完整版)复变函数解析函数

f(z)Ae
成立, 则称当z趋于z0时, f(z)以A为极限，并记做 limf(z)A 或 f(z) A (z z0 ).
zz0
注意: 定义中zz0的方式是任意的.
几何意义
y
(z)
v
w f(z)
z0 d
o
xo
(w)
e
A
u
几何意义: 当变点z一旦进
入z0 的充分小去 心邻域时,它的象
点f(z)就落入A的
(最新整理)(完整版)复变函数解析函数
2021/7/26
1
第二章 解析函数
2.1 复变函数的概念 2.2 解析函数的概念 2.3 解析的充要条件 2.4 初等函数
2.1 复变函数的概念、极限与连续性
复变函数的概念
1. 复变函数的定义 2. 映射的概念 3. 反函数或逆映射
1. 复变函数的定义—与实变函数定义相类似
0)
A
zz0 g(z) l i mg(z) zz0
B
zz0
以上定理用极限定义证!
例1
证明 wx2yi(xy2)在平面上处处 . x2 y, x y2在平面上处处有极限
例2
求 f(z)zz
z 在 z0时的极 . 限 z
f(z)2(xx22yy22)在(0,0)处极限不 . 存在
例3
证 明 f(z)Rez z在z0时 的 极 限.不 存
y (z)
v (w)
w z2
2
o
x
o
u
y (z)
v (w)
w z2
w z2
o
6
x w z2 o
3
u
x2 y2 4
3. 反函数或逆映射

复变函数

1)u( x , y )，v ( x , y )在点( x , y )可微; 2)满足柯西- 黎曼方程：
u v u v ， 。 x y y x
证明:
必要性
f(z)在D内一点z可导，则：
f f ( z z ) f ( z ) f '( z )z ( z )z
比较两边实部与虚部得：
u ax by 1x 2 y v bx ay 2 x 1y
由于 lim ( z ) 0 ，所以
z 0
x 0 y 0
lim 1 0 lim 2 0
x 0 y 0
所以u，v可微，且
lim 其中，A与z无关， z0 ( z ) 0. 则称f(z)在z0处可微。
并称Az为f(z)在z0处的微分。记作 dw Az 可以证明， f(z)在z0处可微的充要条件是f(z)在z0处 可导。且 A f ( z0 )，即 dw f ( z0 )z 由于在dz z ，故dw f ( z0 )dz。

f ( z ) f ( z ) g ( z ) f ( z ) g ( z ) , ( g ( z ) 0) 2 g( z ) [ g( z )]
{ f [ g( z )]} f ( w ) g( z ), 其中w g( z ).
1 f ( z ) , 其中w f ( z )与z ( w )是两个互为反 ( w ) 函数的单值函数，且 ( w ) 0.
h( z0 z ) h( z0 ) z 的极限不存在。 因此，函数h(z)=|z|2仅在z0=0处可导，而在其它点 均不可导. 故它在整个复平面上不解析。
几个重要结论： 1、两个解析函数的和、差、积 、商（分母不为零） 是解析函数。

解析函数的充要条件

u v , u v , (x, y) D. x y y x
定理1,2的另一个版本
利用复数的三角表示形式 z r(cos i sin )
NUDT
§2 解析函数的充要条件
定理1 设函数 f (z) u(r, ) 定iv义(r在,区) 域D内,
则 f (z在) D内一点 z r(cos可导i s的in充)要条件:
举例:多项式, 有理分式函数 解析函数的特性
➢ 解析函数可无限可导 ➢ 非常值解析函数的零点孤立 ➢ 在局部上解析函数是幂级数的和函数
NUDT
§2 解析函数的充要条件
定理1 设函数 f (z) u(x, y)定义iv(在x, y区) 域 内，则 D f (z在) 内D 一点 z 可x导 i的y 充要条件是： 与u(x,在y) 点v(x,可y) 微，并(x,且y)满足柯西—黎曼方程
NUDT
§2 解析函数的充要条件
定理1 设函数 f (z) u(x, y)定义iv(在x, y区) 域 内，则 D f (z在) 内D 一点 z 可x导 i的y 充要条件是： 与u(x,在y) 点v(x,可y) 微，并(x,且y)满足柯西—黎曼方程
u v , u v . x y y x
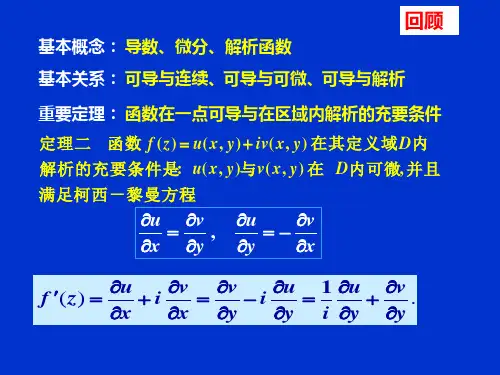
定理2 函数 f (z) u(x, y)在 i区v(域x, y)内解析的D充要条件是： 与 在 u内(x,可y)微，v(x并, y且) 满D足柯西—黎曼方程
即今天的" 和N" "说法,他" 与德国数学
家戴德金,康托一起创立了实数理论. 至此,人们才知道无穷小量只不过是在某 个变化过程中以零为极限的变量.
导数
NUDT
§1 解析函数的概念
可导与连续的关系
连续不一定意味着可导,而可导必然连续.

复变函数课件2-2函数解析的充要条件


(1) w z; ( 2) f ( z ) e x (cos y i sin y ); ( 3) w z Re( z ).
解 (1) w z ,
u x, v y,
u u v v 1, 0, 0, 1. x y x y 不满足柯西－黎曼方程,
5
由于 k 的任意性,
z 1 ki 不趋于一个确定的值 . z 1 ki
h( z0 z ) h( z0 ) lim 不存在. z 0 z
因此 h( z ) z 仅在 z 0 处可导, 而在其他点都 不可导, 根据定义, 它在复平面内处处不解 析.
2
6
例2 解
函数 f ( z ) xy 在点 z 0 不可导.
18
例5 设 f ( z ) u( x , y ) iv( x , y ) 在区域 D 内解
析, 并且 v u , 求 f ( z ).
2
解
u v u 2u , x y y u v u 2 u , y x x
2 2
2
4
z ( z0 z )( z0 z ) z0 z0 z0 z z0 , z z h( z0 z ) h( z0 ) lim 0. (1) z0 0, z 0 z
( 2) z0 0,
令 z0 z 沿直线 y y0 k ( x x0 ) 趋于 z0 , y 1 i 1 ik z x i y x z x iy 1 i y 1 ik x
所以 u 常数, v 常数,
因此 f ( z ) 在区域 D 内为一常数.
21
参照以上例题可进一步证明:
如果 f ( z ) 在区域 D 内解析, 则以下条件彼此等价 . (1) f ( z ) 恒取实值;

复变函数 _第3讲

z 0
lim f ( z 0 z ) f ( z 0 ) ,
即 f ( z ) 在 z 0 连续 .
[证毕]
11
3.求导法则: 由于复变函数中导数的定义与一元实变函 数中导数的定义在形式上完全一致, 并且复变函 数中的极限运算法则也和实变函数中一样, 因而 实变函数中的求导法则都可以不加更改地推广 到复变函数中来, 且证明方法也是相同的. 求导公式与法则:
x
9
2.可导与连续: 函数 f (z) 在 z0 处可导则在 z0 处一定连续, 但 函数 f(z) 在 z0 处连续不一定在 z0 处可导. 证
根据在 z 0 可导的定义
0, 0,
,
使得当 0 | z | 时 ,
有
f ( z0 z ) f ( z0 ) z
f ( z ) 在 z 0 解析 .
如果函数 f ( z )在 区域 D内每一点解析, 则称 f ( z )在 区域 D内解析. 或称 f ( z )是 区域 D 内的一 个解析函数(全纯函数或正则函数 ).
14
2. 奇点的定义
如果函数 f ( z ) 的奇点 . f ( z ) 在 z 0 不解析 , 那末称 z 0 为
4
例1 解
求 f ( z ) z 的导数 .
2
f ( z ) lim
f (z z) f (z) z
z 0
lim
(z z) z
2
2
z 0
z
lim ( 2 z z ) 2 z .
z 0
2 ( z ) 2z
5
例2 解

讨论 f ( z ) Im z 的可导性 .
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
u v 1 u v iii) 求导数： f' ( z ) i x x i y y

前面我们常把复变函数看成是两个实函数拼 成的, 但是求复变函数的导数时要注意, 并不是两个 实函数分别关于x,y求导简单拼凑成的.
二. 举例
例1 判定下列函数在何处可导，在何处解析：
若沿平行于实轴的方式 zቤተ መጻሕፍቲ ባይዱz z ( y0 )
f(z z)f(z) f(z)lim z 0 z [u (x x ,y )iv (x x ,y )] [u (x ,y )iv (x ,y )] lim x 0 x u (x x ,y )u (x ,y ) v (x x ,y )v (x ,y ) lim i lim x 0 x 0 x x
1 u v v u i i y y y y
f ' ( z ) 存在 u v v u i i x x y y u v x y
定义 方程

u x v x
记忆
v u x y
u y v y
Cauchy-Riemann方程
u v v u x y x y
上述条件满足时,有
f ' ( z ) u iv u iu v iu v iv x x x y y y y x
定理2 函数f (z)=u(x, y)+iv(x, y)在D内解析充要 条件是 u(x, y) 和 v(x, y)在D内可微，且 满足Cauchy-Riemann方程
第三讲 解析函数的充要条件 初等函数
§2.2 解析函数的充要条件

1. 解析函数的充要条件

2. 举例
如果复变函数 w = f (z) = u(x, y) + iv(x, y)在定 义域 D内处处可导，则函数 w = f (z) 在 D内解析。 问题 如何判断函数的解析性呢？
本节从函数 u (x , y) 及 v (x , y) 的可导性，探求 函数w = f (z) 的可导性，从而给出判别函数解析的 一个充分必要条件，并给出解析函数的求导方法。
(2)∵ f (z)=ex(cosy +isiny) 则 u=excosy, v= exsiny
u u u v x x e cosy e siny x y x y v v v u x x e siny e cosy x y x y
u v x x f ' ( z ) i e cos y ie sin y f ( z ) x x
故 f (z) ex (cosy i siny)在全平面可导，解析
(3) 设z=x+iy w=x2+y2 u= x2+y2 , v=0 则
u u v v 2 x 2 y 0 0 x y x y
仅在点z = 0处满足C-R条件，故
w z 仅在 z 0处可导，但处处不解析 。
x 2 ( 1 ) w z ; ( 2 ) f ( z ) e (co y i sin y ) ； s ( 3 ) w | z | .
解 (1) 设z=x+iy w=x-iy u=x, v= -y 则
u u 1 0 u v x y v v 0 1 x y x y 故 w z在 全 平 面 不 可 导 ，析 不。 解
u v v u x y x y
称为Cauchy-Riemann方程(简称C-R方程).
定理1 设 f (z) = u (x, y) + iv(x, y)在 D 内有定义， 则 f (z)在点 z = x+iy ∈D处可导的充要条件
是u(x, y) 和 v(x, y) 在点 (x, y ) 可微, 且满足
u v i x x
若沿平行于虚轴的方式 z z z ( x0 )
f (z z) f (z) f (z)lim z 0 z [u (x , y y)iv (x , y y)] [u (x , y)iv (x , y)] lim y 0 i y u (x , y y)u (x , y) v(x , y y)v(x , y) lim i lim y 0 y 0 i y i y
u v v u x y x y

由此可以看出可导函数的实部与虚部有密切 的联系.当一个函数可导时,仅由其实部或虚部就可 以求出导数来.
利用该定理可以判断那些函数是不可导的.
使用时: i) 判别 u(x, y)，v (x, y) 偏导数的连续性， ii) 验证C-R条件.
一. 解析函数的充要条件
设函 w 数 f ( z ) u ( x ,y ) iv ( x ,y ) 在点 z x iy 可 , 则 导
f(z z) f(z) z
[ u ( x x , y y ) iv ( x x , y y )] [ u ( x , y ) iv ( x , y )] x i y
2
x y w u ( x ,y ) iv ( x ,y ) 2 2 i 2 2 x y x y dw 在 z x iy 0 处解析， . 并求 dz
证明 由于在z≠0处，u(x,y)及v(x,y)都是可微函数， 且满足C-R条件：
2 2 u v y x u v 2 xy 2 , 2 22 2 2 x y (x y ) y x (x y )