下载文档原格式
专题二函数考点4 函数单调性的5种判断方法及3个应用方向【方法点拨】一、函数单调性的判断及解决应用问题的方法1.判断函数单调性的常用方法(1)定义法；（2）图象法；(3)利用函数的性质“增+增=增，减+减=减”判断；(4)复合函数的单调性根据“同增异减”判断；(5)导数法2.求函数的单调区间先定定义域，在定义域内求单调区间.单调区间不连续时，要用“和”或“，“连接，不能用“U”连接.3.单调性的应用的三个方向(1)比较大小：将自变量转化到同一个单调区间内，利用函数的单调性比较大小；(2)解函数型不等式：利用函数单调性，由条件脱去“f”；(3)求参数值或取值范围：利用函数的单调性构建参数满足的方程(组)、不等式(组).【高考模拟】1．函数()||1f x x =-与()()2g x x x =-的单调递增区间分别为（ ） A ．[1，+∞)，[1，+∞) B ．(﹣∞，1]，[1，+∞) C ．(1，+∞)，(﹣∞，1] D ．(﹣∞，+∞)，[1，+∞)【答案】A 【分析】先对()f x ，()g x 进行化简，再求单调区间即可. 【解析】 解：()1,111,1x x f x x x x -≥⎧=-=⎨-+<⎩，()f x ∴在[)1,+∞上单调递增，()()222()211g x x x x x x -=-==--， ()g x ∴在[)1,+∞上单调递增，故选：A.2．函数y =）A ．3,2⎛⎤-∞- ⎥⎝⎦B ．3,2⎡⎫-+∞⎪⎢⎣⎭C ．[)0,+∞D ．(],3-∞-【答案】D 【分析】求出函数y =y =.【解析】由题意，230x x +≥，可得3x ≤-或0x ≥，函数y =(][),30,-∞-⋃+∞，令23t x x =+，则外层函数y =[)0,+∞上单调递增，内层函数23t x x =+在上(],3-∞-单调递减，在[)0,+∞上单调递增，所以，函数y =(],3-∞-.故选：D. 【点睛】方法点睛：求解函数的单调区间一般有以下几种方法：一是图象法，主要适用与基本初等函数及其在基本初等函数的基础上进行简单变化后的函数以及分段函数，可以借助图像来得到函数的单调区间；二是复合函数法，主要适用于函数结构较为复杂的函数，采用换元的思想将函数解析式分解为多层，利用同增异减的原理来求解；三是导数法，对于可导函数，可以解相应的导数不等式来求解函数的单调区间.3．函数()f x 在区间()4,7-上是增函数，则使得()3=-y f x 为增函数的区间为（ ） A ．()2,3- B ．()1,7-C ．()1,10-D ．()10,4--【答案】C 【分析】先将函数()3=-y f x 看作函数()f x 向右平移3个单位所得到，再判断增区间即可. 【解析】函数()3=-y f x 可以看作函数()f x 向右平移3个单位所得到，故由函数()f x 在区间()4,7-上是增函数，得()3=-y f x 在区间()1,10-上是增函数. 故选：C.4．函数()2f x x x =-的单调减区间是（ ） A ．[]1,2 B ．[]1,0-C ．[]0,2D ．[2,)+∞【答案】A 【分析】将函数写成分段函数的形式，即()(2),2,(2),2,x x x f x x x x -⋅≥⎧=⎨-⋅<⎩再根据解析式得到函数的单调区间；【解析】()(2),2,(2),2,x x x f x x x x -⋅≥⎧=⎨-⋅<⎩∴直接通过解析式，结合二次函数图象得：(,1),(2,)-∞+∞递增，在[]1,2递减，故选：A.5．函数f (x )=x 2+2(a -1)x +2在区间(-∞，4)上递减，则a 的取值范围是（ ） A ．[3,)-+∞ B ．(,3]-∞- C ．(,5)-∞ D ．[3,)+∞【答案】B 【分析】利用二次函数的性质，比较对称轴和区间端点的大小，列不等式可得a 的取值范围． 【解析】函数f(x)的对称轴是1x a =-，开口向上，则14a -≥，解得3a ≤- 故选：B6．若函数2()()f x ax a -=∈R 在(0,)+∞上单调递增，则实数a 的取值范围为（ ）． A ．(1,)+∞ B ．(,1)-∞ C ．(0,)+∞ D ．(,0)-∞【答案】D 【分析】直接由单调性的定义求解即可 【解析】解：任取12,(0,)x x ∈+∞，且12x x <，因为函数2()()f x ax a -=∈R 在(0,)+∞上单调递增，所以12()()f x f x <，即22120ax ax ---<，所以221211()0a x x -<，21212212()()0x x x x a x x +-⋅<⋅， 因为120x x <<，所以210x x +>，210x x ->，22120x x ⋅>，所以0a <． 故选：D7．如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上单调递减，那么实数a 的取值范围是（ ） A ．3a ≤- B ．3a ≥-C ．5a ≤D ．5a ≥【答案】A【分析】求出二次函数的对称轴，根据单调区间与对称轴之间的关系建立条件，即可求出a 的取值范围． 【解析】 解：二次函数2()2(1)2f x x a x =+-+的对称轴为2(1)(1)12a x a a -=-=--=-，抛物线开口向上，∴函数在(-∞，1]a -上单调递减，要使()f x 在区间(-∞，4]上单调递减， 则对称轴14a -， 解得3a-．故选：A ． 【点睛】本题主要考查二次函数的图象和性质，根据二次函数单调性与对称轴之间的关系是解决本题的关键． 8．“1m ”是“函数1()2ln f x x mx x=-+单调递减”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】A 【分析】求出()y f x =的导函数，利用()y f x =单调递减，则()0f x '≤恒成立，求出m 的范围，比较所求范围和条件中给定范围的关系，得出结论. 【解析】 由221()f x m x x '=--，若函数()y f x =单调递减，必有当(0,)x ∈+∞时，2210m x x--≤恒成立，可化为2111m x ⎛⎫≥--+ ⎪⎝⎭，可得m 1≥．故“1m ”是“函数1()2ln f x x mx x =-+单调递减”的充分不必要条件. 故选：A. 9．若函数2()1f x x =-的定义域是(﹣∞，1)∪[2，5)，则其值域为（ ） A ．(﹣∞，0)B ．(﹣∞，2]C ．10,2⎛⎤ ⎥⎝⎦D ．1(,0),22⎛⎤-∞⋃ ⎥⎝⎦【答案】D 【分析】分x<1和x ∈[2，5)两种情况，利用反比例函数的性质得出函数的值域． 【解析】由题意可得：当x<1时，则x ﹣1<0所以y ∈(﹣∞，0) 当x ∈[2，5)时，则x ﹣1∈[1，4)，所以y ∈1,22⎛⎤⎥⎝⎦所以函数的值域为1(,0),22⎛⎤-∞⋃ ⎥⎝⎦.故选：D.10．若关于x 的不等式342xx a+-在[0x ∈，1]2上恒成立，则实数a 的取值范围是（ ）A ．(-∞，1]2-B ．(0，1]C ．1[2-，1]D ．[1，)+∞【答案】D 【分析】利用参数分离法进行转化，构造函数求函数的最大值即可得到结论. 【解析】解：由题意知，342xx a +-在(0x ∈，1]2上恒成立，设3()42x f x x =+-，则函数在102⎛⎤ ⎥⎝⎦，上为增函数，∴当12x =时，()12max 113()4211222f x f ==+-=-=， 则1a ， 故选：D . 【点睛】 关键点睛：本题的关键是将已知不等式恒成立问题，通过参变分离得到参数的恒成立问题，结合函数的单调性求出最值.11．若01m n <<<且1mn =，则2m n +的取值范围是（ ）A．)+∞ B ．[3,)+∞C．)+∞D ．(3,)+∞【答案】D 【分析】先利用已知条件构造函数()2(),01f m m m m+<<=，再求其值域即得结果. 【解析】由01m n <<<且1mn =知，22m n m m +=+，故设()2(),01f m m m m+<<=， 设1201m m <<<，则()1212121212222()()1f m f m m m m m m m m m ⎛⎫⎛⎫⎛⎫-=+-+=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 12120,01m m m m -<<<，即1222m m >，故()1212210m m m m ⎛⎫--> ⎪⎝⎭，即12()()f m f m >， 函数2()f m m m =+在()0,1上单调递减，2(1)131f =+=，故函数的值域为(3,)+∞. 故选：D. 【点睛】方法点睛：利用定义证明函数单调性的方法（1）取值：设12,x x 是该区间内的任意两个值，且12x x <； （2）作差变形：即作差，即作差12()()f x f x -，并通过因式分解、配方、有理化等方法，向有利于判断符号的方向变形； （3）定号：确定差12()()f x f x -的符号；（4）下结论：判断，根据定义作出结论. 即取值---作差----变形----定号----下结论. 12．函数()()2404xf x x x x x =++>+的最小值为（ ） A ．2 B ．103C ．174D ．265【答案】C 【分析】 令4t x x =+，利用基本不等式求得4t ≥，构造函数()1g t t t=+，证明出函数()g t 在[)4,+∞上为增函数，由此可求得函数()f x 的最小值. 【解析】令4t x x =+，则21144x x t x x==++，因为0x >，所以44t x x =+≥=，又2414x y x t x x t =++=++，令()1g t t t=+，其中4t ≥， 任取1t 、[)24,t ∈+∞且12t t >，即124t t >≥，则()()()()()121221121212121212111t t t t t t g t g t t t t t t t t t t t --⎛⎫⎛⎫--=+-+=-+= ⎪ ⎪⎝⎭⎝⎭， 124t t >≥，120t t ∴->，121t t >，()()120g t g t ∴->，即()()12g t g t >，所以，函数()g t 在[)4,+∞上为增函数，因此，()()min 1174444f xg ==+=. 故选：C. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件： （1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.13．若函数1y ax =+在区间[]1,3上的最大值是4，则实数a 的值为（ ） A ．-1 B ．1C ．3D ．1或3【答案】B 【分析】分0a >和0a <两种情况求解，0a >时，1y ax =+在区间[]1,3上为增函数，从而可求出其最大值，当0a <时，1y ax =+在区间[]1,3上为减函数，从而可求出其最大值，进而可得答案 【解析】解：当0a >时，1y ax =+在区间[]1,3上为增函数，则当3x =时，y 取得最大值，即314a +=，解得1a =；当0a <时，1y ax =+在区间[]1,3上为减函数，则当1x =时，y 取得最大值，即14a +=，解得3a =舍去， 所以1a =， 故选：B14．函数2y ax =+在[1，2]上的最大值与最小值的差为3，则实数a 为（ ） A ．3 B ．-3 C ．0 D ．3或-3【答案】D 【分析】讨论a 的取值，判断函数的单调性，求出函数的最值，作差即可求解. 【解析】解：①当0a =时，2=2y ax =+，不符合题意；②当0a >时，2y ax =+在[]1,2上递增，则()()2223a a +-+=，解得3a =； ③当0a <时，2y ax =+在[]1,2上递减，则()()2223a a +-+=，解得3a =-．综上，得3a =±， 故选：D ．15．已知函数24()2tx t f x x --+=+在区间[1,2]-上的最大值为2，则实数t 的值为（ ）A ．2或3B ．1或3C ．2D ．3【答案】A 【分析】 函数()24422tx t f x t x x --+==-+++，4[1,2],[1,4]2x t t t x ∈--+∈--+，根据绝对值的最大值为2进行分类讨论检验即可. 【解析】 由题函数()24422tx t f x t x x --+==-+++，4[1,2],[1,4]2x t t t x ∈--+∈--+ ()24422tx t f x t x x --+==-+++的最大值为4t -或1t -当41t t -≥-时，即52t ≤时，最大值42t -=解得：2t =；当41t t -<-时，即52t >时，最大值12t -=解得：3t = 综上所述：t 的值等于2或3. 故选：A 【点睛】解决本题的关键是利用单调性求出42t x -++的范围，再结合绝对值的性质进行求解. 16．若函数12,02()(21)3,2log x x f x a x a x <<⎧⎪=⎨⎪-+⎩的值域为R ，则实数a 的取值范围为（ ） A ．1[2，1)B ．1(0,)7C ．1[7，1)2D ．1[2，1]【答案】C 【分析】根据分段函数的值域为R ，具有连续性，由12log y x =是减函数，可得(21)3y a x a =-+也是减函数，故得210a -<，(21)231a a -⨯+-，可得答案. 【解析】解：函数12,02()(21)3,2log x x f x a x a x <<⎧⎪=⎨⎪-+⎩的值域为R ， 由12log y x =是减函数，(21)3y a x a ∴=-+也是减函数，故得210a -<， 解得：12a <， 函数()f x 的值域为R ，12(21)23log 21a a -⨯+=-，解得：17a. ∴实数a 的取值范围是1[7，1)2.故选：C .17．若函数()f x 是R 上的减函数，0a >，则下列不等式一定成立的是（ ） A ．2()()f a f a < B ．1()f a f a ⎛⎫<⎪⎝⎭C ．()(2)f a f a <D ．2()(1)f a f a <-【答案】D 【分析】根据函数单调性，以及题中条件，逐项判断，即可得出结果. 【解析】因为函数()f x 是R 上的减函数，0a >，A 选项，()21a a a a -=-，当1a >时，2a a >，所以2()()f a f a <；当01a <<时，2a a <，所以2()()f a f a >，即B 不一定成立； B 选项，当1a >时，1a a >，所以1()f a f a ⎛⎫< ⎪⎝⎭；当01a <<时，1a a <，所以1()f a f a ⎛⎫> ⎪⎝⎭，即B 不一定成立；C 选项，0a >时，2a a >，则()(2)f a f a >，所以C 不成立；D 选项，()2221311024a a a a a ⎛⎫--=-+=-+> ⎪⎝⎭，则21a a >-；所以2()(1)f a f a <-，即D一定成立. 故选：D.18．已知函数2()f x x bx c =++，且(2)()f x f x +=-，则下列不等式中成立的是（ ） A ．(4)(0)(4)f f f -<< B ．(0)(4)(4)f f f <-< C ．(0)(4)(4)f f f <<- D ．(4)(0)(4)f f f <<-【答案】C 【分析】由(2)()f x f x +=-，即可得到()f x 图象的对称轴为1x =，所以根据图象上的点离对称轴的距离即可比较出(0),(4),(4)f f f -的大小关系. 【解析】由(2)()f x f x +=-得()f x 图象的对称轴为1x =，所以()f x 在(,1]-∞上单调递减，在[1,)+∞上单调递增，且(4)(2)f f =-， 所以(0)(2)(4)(4)f f f f <-=<-， 故选：C. 【点睛】方法点睛：该题考查的是有关函数值的比较大小的问题，解题方法如下：（1）首先根据题中所给的函数解析式，判断函数类型，根据题中所给的条件，判断出函数图象的对称轴；（2）利用对称性，将自变量所对应的函数值进行转换； （3）根据函数的单调性求得结果.19．若定义在R 上的偶函数()f x 在[)0,+∞上是减函数，则下列各式一定成立的是（ ） A ．()()06f f < B ．()()32f f -> C ．()()13f f -> D ．()()58f f -<-【答案】C 【分析】由偶函数及在[)0,+∞上是减函数，知在(,0]-∞上是增函数，即可判断各项的正误. 【解析】A ：在[)0,+∞上是减函数，即()()06f f >，错误；B ：(3)(3)f f -=，()f x 在[)0,+∞上是减函数，有()()32f f <，即()()32f f -<，错误； C ：(1)(1)f f -=，()f x 在[)0,+∞上是减函数，有()()31f f <，即()()13f f ->，正确； D ：由题意，()f x 在(,0]-∞上是增函数，()()58f f ->-，错误； 故选：C20．设函数()f x 是(),-∞+∞上的减函数，又若a R ∈，则（ ） A ．()()2f a f a >B ．()()2f a f a < C ．()()2f a a f a +<D ．()()211f a f +≤【答案】D 【分析】利用特殊值法可判断ABC 选项的正误，利用函数的单调性可判断D 选项的正误. 【解析】对于A 选项，取0a =，则2a a =，()()2f a f a ∴=，A 选项错误； 对于B 选项，取0a =，则2a a =，所以，()()2f af a =，B 选项错误；对于C 选项，取0a =，则2a a a +=，所以，()()2f a a f a +=，C 选项错误；对于D 选项，对任意的a R ∈，211a +≥，所以，()()211f a f +≤，D 选项正确.故选：D.21．函数()f x 的定义域为,(1)0,()f f x '=R 为()f x 的导函数，且()0f x '>，则不等式()()20x f x ->的解集是（ ）A ．(,1)(2,)-∞⋃+∞B ．(,1)(1,)-∞⋃+∞C ．(0,1)(2,)+∞D ．(,0)(1,)-∞⋃+∞【答案】A 【分析】依题意可得()f x 再定义域上单调递增，又()10f =，即可得到1x <时，()0f x <；1 x >时，()0f x >；再分类讨论分别计算最后取并集即可；【解析】解：由题意可知()f x 在(),-∞+∞单调递增，又()10f =，1x <时，()0f x <；1 x >时，()0f x >； 对于()()2 0x f x ->，当2x >时，不等式成立， 当12x <<时，()20, 0x f x -<>，不等式不成立； 当1x <时，20x -<，且()0f x <， 不等式成立不等式的解集(,1)(2,)-∞⋃+∞ 故选：A .22．已知定义在R 上的函数()f x 的导函数为'()f x ，且满足'()()0f x f x ->，()20212021f e =，则不等式1ln 3f x ⎛⎫<⎪⎝⎭）A ．()6063,e +∞B ．()20210,eC ．()2021,e +∞D ．()60630,e【答案】D 【分析】由题意构造新函数()()xf x F x e =，得到函数的单调性，对问题进行变形，由单调性转化为求解不等式问题，即可得到结果 【解析】 由题可设()()x f x F x e=，'()()0f x f x ->，则2'()()'()()'()0x x x xf x e f x e f x f x F x e e--==>， 所以函数()F x 在R 上单调递增，2021(2021)(2021)1f F e==，将不等式1ln 3f x ⎛⎫< ⎪⎝⎭1ln 311ln ln 3311ln ln 33x x x f x f x e e e ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⋅=， 可得1ln 13F x ⎛⎫< ⎪⎝⎭，即1ln (2021)3F x F ⎛⎫< ⎪⎝⎭，有1ln 20213x <，故得60630x e <<，所以不等式1ln 3f x ⎛⎫< ⎪⎝⎭()60630,e ，故选：D. 【点睛】关键点睛：本题的解题关键是构造新函数，然后运用函数单调性求解不等式，通常情况构造新函数的形式如：()()xf x F x e =、()()F x xf x =或者()()f x F x x =等，需要结合条件或者问题出发进行构造.23．已知函数2()121xf x =-+，且()41(3)xf f ->，则实数x 的取值范围是（ ）． A ．(2,)+∞ B ．(,2)-∞C ．(1,)+∞D ．(,1)-∞【答案】D 【分析】用导数判断函数()f x 的单调性，再解不等式即可. 【解析】 因为()()22ln 2021x xf x -=<+'，所以函数2()121x f x =-+在R 上单调递减， 由于()41(3)xf f ->所以413x-<，得1x <故选：D 【点睛】关键点点晴：判断函数()f x 的单调性是解题的关键.24．已知定义在R 上的函数()f x 满足()13f =，对x ∀∈R 恒有()2f x '<，则()21f x x ≥+的解集为（ ） A ．[)1,+∞ B ．(],1-∞C ．()1,+∞D ．(),1-∞【答案】B 【分析】构造新函数()()21F x f x x =--，利用导数判断()F x 单减，又(1)0F =可解1x ≤. 【解析】令()()21F x f x x =--，则()()2F x f x ''=-， 又因为对x ∀∈R 恒有()2f x '< 所以()()20F x f x ''=-<恒成立， 所以()()21F x f x x =--在R 上单减. 又(1)(1)210F f =--=， 所以()0F x ≥的解集为(],1-∞ 故选：B 【点睛】利用单调性解不等式通常用于： (1)分段函数型不等式； (2)复合函数型不等式；(3)抽象函数型不等式； (4)解析式较复杂的不等式；25．已知函数f (x ) f (2a 2－5a ＋4)<f (a 2＋a ＋4) ，则实数a 的取值范围是（ ） A ．1,2⎛⎫-∞ ⎪⎝⎭∪(2,＋∞)B ．[2,6)C ．10,2⎛⎤ ⎥⎝⎦∪[2,6)D ．(0,6)【答案】C 【分析】由解析式知()f x 在定义域上递增，由已知函数不等式有2222544a a a a ≤-+<++，即可求解a 的取值范围. 【解析】由题意，()f x 在[2,)+∞上单调递增，∵22(254)(4)f a a f a a -+<++，即2222544a a a a ≤-+<++， ∴260a a -<或22520a a -+≥，可得26a ≤<或102a <≤. 故选：C 【点睛】关键点点睛：利用函数的单调性，列不等式求参数的范围.易错点是定义域容易被忽略.26．已知函数()f x 的图象关于y 轴对称，当0x ≥时，()f x 单调递增，则不等式(2)(1)f x f x >-的解集为__________． 【答案】1(,1)(,)3-∞-⋃+∞ 【分析】由题意可得()f x 为偶函数，再由偶函数的性质可将(2)(1)f x f x >-，转化为(2)(1)f x f x >-，再由当0x ≥时，()f x 单调递增，可得21x x >-，从而可求出x 的范围 【解析】解：依题意，()f x 为偶函数，当0x ≥时，()f x 单调递增，要满足(2)(1)f x f x >-，则要求21x x >-，两边平方得22412x x x >-+，即23210x x +->，即(1)(31)0x x +->，解得1(,1)(,)3x ∈-∞-⋃+∞． 故答案为：1(,1)(,)3-∞-⋃+∞．27．设()xf x a x =+，若()36f =，则不等式()()21f x f x ->的解集为____________.【答案】()1,+∞ 【分析】先由()36f =，解出a ，讨论()xf x a x =+的单调性，利用函数单调性解不等式即可.【解析】因为()xf x a x =+，且()36f =，，所以33a =，解得1a =>.()(),ln 1x x f x f a x a x a =+∴=+' ln 0,ln 111,x x a a a a a >∴>∴>+，()x f x a x ∴=+在R 上单增.()()21f x f x ->可化为：21x x ->解得：1x >.不等式()()21f x f x ->的解集为()1,+∞ 故答案为：()1,+∞ 【点睛】利用单调性解不等式通常用于： (1)分段函数型不等式；(2)复合函数型不等式；(3)抽象函数型不等式；(4)解析式较复杂的不等式；28．已知定义域为R 的奇函数()f x 在区间(0,)+∞上为严格减函数，且()20f =，则不等式(1)01f x x +≥-的解集为___________.【答案】[]3,1-- 【分析】先由定义域为R 的奇函数()f x 在区间(0,)+∞上为严格减函数，且()20f =，画出()f x 的草图，结合图像对(1)01f x x +≥-进行等价转化，解不等式即可.【解析】()f x 是定义域为R 的奇函数，且在区间(0,)+∞上为严格减函数，有()20f =，∴()f x 在区间(,0)-∞上为严格减函数且()20f =，可作出()f x 的草图：不等式(1)01f x x +≥-可化为：()1010x f x ->⎧⎨+≥⎩或()1010x f x -<⎧⎨+≤⎩对于()1010x f x ->⎧⎨+≥⎩，当1x >时()12,10x f x +>+<，无解；对于()1010x f x -<⎧⎨+≤⎩，当1x <时()12,10x f x +<+≤，由图像观察，210x -≤+≤解得：31x -≤≤- 所以不等式(1)01f x x +≥-的解集为[]3,1--.故答案为：[]3,1-- 【点睛】常见解不等式的类型：(1)解一元二次不等式用图像法或因式分解法； (2)分式不等式化为标准型后利用商的符号法则； (3)高次不等式用穿针引线法； (4)含参数的不等式需要分类讨论．29．已知函数()()23log 440f x ax x =-+>在x ∈R 上恒成立，则a 的取值范围是_________.【答案】4,3⎛⎫+∞ ⎪⎝⎭【分析】由题意，把函数()()23log 440f x ax x =-+>在x ∈R 上恒成立转化为2430ax x -+>对x ∈R上恒成立，列不等式解得a 的范围. 【解析】()()23log 440f x x x α=-+>恒成立，即()2233log 44log 1430ax x ax x -+>⇔-+>恒成立，所以0a =时显然不成立.当0a ≠时()0Δ16120a a >⎧⎨=-<⎩得43a <，所以4,3a ⎛⎫∈+∞ ⎪⎝⎭.故答案为：4,3⎛⎫+∞ ⎪⎝⎭【点睛】（1）求参数的范围是常见题型之一，处理的方法有两种：①不分离参数，直接求最大值或最小值，解不等式；②分离参数法.（2）解指、对数型的不等式，通常化为同底的结构，利用函数的单调性解不等式.30．设函数3,1()1+1,1x x f x x x x ≤⎧⎪=⎨->⎪⎩，则不等式()26()f x f x ->的解集为_________．【答案】()3,2- 【分析】先判断函数的单调性，再解抽象不等式. 【解析】当1x >时，31+1y x x=-是增函数，此时1y >； 当1x ≤时， y x =是增函数，此时1y ≤， 所以函数()f x 是单调递增函数，()()2266f x f x x x ->⇔->，解得：32x -<<，所以不等式的解集是()3,2-. 故答案为：()3,2-。
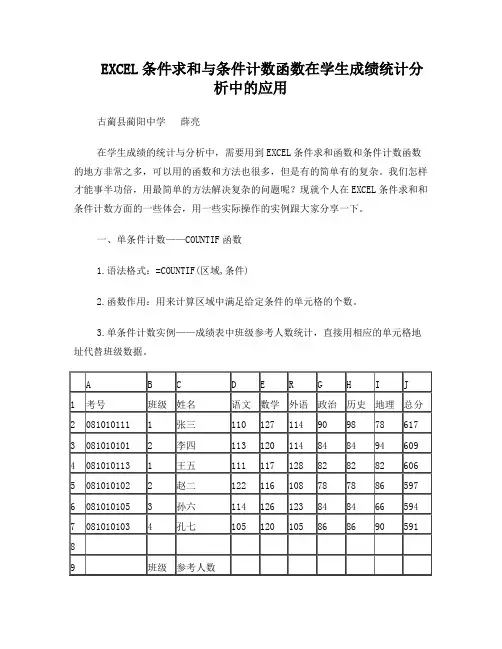
EXCEL条件求和与条件计数函数在学生成绩统计分析中的应用古蔺县蔺阳中学薛亮在学生成绩的统计与分析中，需要用到EXCEL条件求和函数和条件计数函数的地方非常之多，可以用的函数和方法也很多，但是有的简单有的复杂。
我们怎样才能事半功倍，用最简单的方法解决复杂的问题呢？现就个人在EXCEL条件求和和条件计数方面的一些体会，用一些实际操作的实例跟大家分享一下。
一、单条件计数——COUNTIF函数1.语法格式：=COUNTIF(区域,条件)2.函数作用：用来计算区域中满足给定条件的单元格的个数。
3.单条件计数实例——成绩表中班级参考人数统计，直接用相应的单元格地址代替班级数据。
例如：在上面的成绩表中要统计1、2、3、4班的参考人数。
也许有人会在C10、C11、C12、C13中分别输入公式“=COUNTIF(B2:B7,"=1")”、“=COUNTIF(B2:B7,"=2")”、“=COUNTIF(B2:B7,"=3")”、“=COUNTIF(B2:B7,"=4")”，这样做当然没有错，是常规方法，但是如果是30个班、40个班或者更多呢，那就有点麻烦了。
我们其实有更简单的方法——直接引用班级单元格地址。
首先，在C10中输入公式“=COUNTIF($B$2:$B$7,"="&B10)”，然后双击C10右下角填充句柄复制公式就可以了，C11、C12、C13中公式就直接变成了“=COUNTIF($B$2:$B$7,"="&B11)”、“=COUNTIF($B$2:$B$7,"="&B12”、“=COUNTIF($B$2:$B$7,"="&B13)”。
因为B2：B7这个区域是固定不变的，为了复制公式时不发生变化，我们就直接写成绝对引用形式$B$2:$B$7。
解析函数的主要性质综述作者：安辉燕来源：《科学导报》2017年第75期一、导引解析函数是一类具有某种特性的可微函数，它将我们所熟悉的数学分析中的一些内容推广到复数域上并研究其性质。
本文通过搜集材料，系统总结了解析函数的几个主要性质：解析函数的唯一性、零点的孤立性、零点的分布问题、解析函数在无穷远点的性质、解析变换的特征及解析函数、共轭解析函数和复调和函数之间的关系，并通过举例进行了深入、详细的分析。
二、预备知识1.定义如果函数在区域D内是可微的，则称为区域D内的解析函数。
复变函数中解析函数的充要条件有多种形式，最常见的有以下几种。
2.定理函数在区域D内解析的充要条件：A（1）二元函数在区域D内可微；（2）在D内满足方程。
B（3）在D内连续；（4）在D内满足方程。
C 在D内任意一点的邻域内可以展成的幂级数，也就是泰勒级数。
D C为D内任意一条周线，则。
三、解析函数的主要性质1.解析函数的唯一性定理（解析函数的唯一性）如果函数在区域D内解析，是D内彼此不同的点，并且点列的极限点，若有，则在D内必有。
根据定理我们可得到以下结论：推论1 如果函数在区域D内解析，且在区域内某点的邻域内有，则在D内必有。
推论2 如果函数在区域D内解析，且在区域D内某一曲线上有，则在内必有。
2.解析函数零点的孤立性定理如果在内的解析函数不恒为零，是的一个零点，则必存在的一个邻域使得在其中无其他零点。
（即：不恒为零的解析函数的零点具有孤立性）此性质是解析函数的特殊性质，实函数不具有此性质。
3. 解析函数零点的分布问题解析函数的零点的分布问题是复变函数论中的一个重要问题，一下就复多项式的零点可以全部分布在一个指定的区域内这个问题进行讨论。
定理1若复平面上多项式在虚轴上无零点，则它的零点全分布在右半平面上的充要条件为。
定理2若复平面上多项式在实轴上无零点，则它的零点全分布在上半平面的充要条件为。
四、解析变换的特性解析函数的特性是从几何的角度对解析函数的性质和应用进行讨论。
三角函数的性质及其应用 编稿：李霞 审稿：孙永钊【考纲要求】1、了解函数sin()y A x ωϕ=+的物理意义；能画出sin()y A x ωϕ=+的图象，了解参数A ，ω，ϕ对函数图象变化的影响.2、了解三角函数是描述周期变化现象的重要函数模型，会用三角函数解决一些简单实际问题. 【知识网络】【考点梳理】考点一、函数sin()y A x ωϕ=+(0A >,0ω>)的图象的作法1.五点作图法：作sin()y A x ωϕ=+的简图时，常常用五点法，五点的取法是设t x ωϕ=+，由t 取0、2π、π、32π、2π来求相应的x 值及对应的y 值，再描点作图。
2．图象变换法：（1）振幅变换:把sin y x =的图象上各点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A 倍（横坐标不变），得到sin y A x =的图象；（2）相位变换:把sin y A x =的图象上所有点向左(ϕ>0)或向右(ϕ<0)平行移动|ϕ|个单位，得到sin()y A x ϕ=+的图象；（3）周期变换:把sin()y A x ϕ=+的图象上各点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的ω1倍（纵坐标不变），可得到sin()y A x ωϕ=+的图象.（4）若要作sin()y A x b ϕ=++，可将sin()y A x ϕ=+的图象向上(0)b >或向下(0)b <平移b 个单位，可得到sin()y A x b ϕ=++的图象．记忆方法仍为“左加右减，上正下负，纵伸(A>1)横缩(ω>1)”。
要点诠释：由sin y x =的图象利用图象变换作函数sin()y A x ωϕ=+的图象时要特别注意：当周期变换和相位变换的先后顺序不同时，原图象沿x 轴的伸缩量有区别.图象的作法三角函数的性质及其应用图象的性质考点二、sin()y A x ωϕ=+的解析式 1. sin()y A x ωϕ=+的解析式sin()y A x ωϕ=+(0A >, 0ω>)，[0,)x ∈+∞表示一个振动量时，A 叫做振幅，2T πω=叫做周期，12f T ωπ==叫做频率，x ωϕ+叫做相位，0x =时的相位ϕ称为初相. 2. 根据图象求sin()y A x ωϕ=+的解析式求法为待定系数法，突破口是找准五点法中的第一零点(,0)ϕω-. 求解步骤是先由图象求出A 与T ，再由2Tπω=算出ω，然后将第一零点代入0x ωϕ+=求出ϕ. 要点诠释：若图象未标明第一零点，就只能找特殊点用待定系数法计算. 考点三、函数sin()y A x ωϕ=+(0A >,0ω>)的性质1. 定义域: x R ∈,值域:y ∈[-A,A]. 2．周期性: 2T πω=3. 奇偶性:2k πϕπ=+时为偶函数；k ϕπ=时为奇函数，k Z ∈.4．单调性:单调增区间:[ωϕππωϕππ-+--22,22k k ] , k Z ∈ 单调减区间:[ωϕππωϕππ-+-+232,22k k ] , k Z ∈ 5. 对称性:对称中心(ωϕπ-k ,0)， k Z ∈；对称轴x=ωϕππ-+2k ，k Z ∈6．最值: 当22x k πωϕπ+=+即22k x ππϕω+-=时，y 取最大值A当22x k πωϕπ+=-即22k x ππϕω--=时，y 取最小值-A ．(k Z ∈).要点诠释：①求周期、单调区间、最值时一般先将函数式化为sin()y A x ωϕ=+，要特别注意A 、ω的正负，再把x ωϕ+看作一个整体，并结合基本三角函数的图象和性质解出即可；利用单调性比较三角函数大小一般要化为同名函数,并且在同一单调区间；②整体代换和数形结合是三角函数学习中重要的思想方法，在学习中，很多三角函数的问题都是通过整体代换并观察基本三角函数的图象而得到的。
目录摘要 (1)关键词 (1)Abstract (1)Keywords (1)引言 (1)1.函数解析的定义 (1)1.1定义 (1)1.2初等函数的解析性 (2)2. 函数解析的理论 (3)2.1函数在区域D内解析的定理 (3)2.2函数在区域D内解析的第一个等价定理 (4)2.3函数在区域D内解析的第二个等价定理 (5)2.4函数在区域D内解析的第三个等价定理 (5)2.5函数在区域D内解析的第四个等价定理 (7)结语 (8)参考文献 (8)函数在区域内解析的条件及应用学生姓名：杨玉亲 学号：20095031161数学与信息科学学院 数学与应用数学专业指导教师:张萍 职称：讲师摘 要：本文总结了函数解析的5种等价定理，研讨了它们的应用关键词：初等函数；解析函数；函数在区域D 内解析Function in the region and application of analytical conditionsAbstract: This paper summarizes the analysis of five kinds of function equivalence theorem, and discusses their applications. Key Words ：Elementary Functions ；Analytic functions ；Analytic function within the regional D.引言在区域上处处可导的复变函数，我们称这类函数为解析函数，这类函数具有一系列非常重要的特征.虽然单变量复函数可导的概念与单变量实函数可导的概念在形式上完全一样，但在区域上处处可导的复函数与在区间上处处可导的实函数相比较，前者所具有的特征比后者更为深刻和丰富.本课题主要研究了函数在区域D 内解析的条件及应用问题，以下从六个方面给予了分析与概括.1. 函数解析的定义1.1定义 若()f z 在0z 点的某一个邻域0()u z 内处处可导，则称()f z 在0z 点解析，并称0z 是()f z 的解析点.由定义可以推出：若函数()f z 在0z 点解析，则一定存在一个邻域0()u z ，在0()u z 内任意一点1z 处()f z 解析，事实上1z 是0()u z 的内点，因而存在邻域1()u z 0()u z ，使()f z 在1()u z 内处处可导，于是按定义()f z 在1z 点解析.由以上结果进而可以推出：若函数()f z 在一区域D 内处处可导，则根据定义，()f z 在D 内每一点都解析，这样的函数我们称之为解析函数，而D 称为()f z 的解析性区域，按照这一称呼，()f z 若在一点0z 解析，则()f z 是0z 的某一邻域0()u z 上的解析函数.更一般的说，若()f z 是点集E 上的解析函数，按定义()f z 应在复盖点集E 的一个领域集上处处解析，例如E 是某一光滑曲线L ，则“()f z 在L 上解析”实际上表明()f z 在包含L 的一个区域上处处解析.再如E 是一闭区域D ，则“()f z 在闭区域D 上解析”实际上表明()f z 在包含D 的一个区域D '上处处解析.1.2 初等函数的解析性由解析定义及导数性质可知：区域D 上两个解析函数的和、差、积、商（分母不为零）仍是解析函数.另外解析函数的复合函数仍是解析函数；单叶解析函数的反函数一定是解析函数.（1）多项式，指数函数z e ，正弦和余弦函数sin z ，cos z 等函数在整个复平面上处处可导，因而按定义它们在整个复平面上处处解析，在整个复平面上解析的函数称之为整函数.（2）既约分式函数()()()P z R z Q z =显然在整个复平面上除去的全部零点处处解析。
即在其定义域上解析，其他单值初等函数也都在其定义域上解析，例如sin tan cos zz z =则在整个复平面除去使cos z 为零的点之处处处解析，以后称使函数()f z 不解析的点为的奇点.（3）对于初等多值函数，我们已知其每一个单值连续分支在其可单值分解区域上处处可导，因而由定义可知多值函数在其可单值分解区域中的每一个单值连续分支都是解析函数，我们称之为多值函数的单值解析分支，例如Lnz ω=在沿负半实轴 割开的平面区域D 上可划分为单值解析分支()ln ||arg 2(0,1,1,)k Lnz z i z k i k ωπ==++=-+⋅⋅⋅ 它们的导函数都相同，为1zω'=. 显然负半实轴上的点都是每一个单值解析分支的奇点，在0z =的任一领域内Lnz ω=不可能划分为单值连续分支，当然也不能划分为单值解析分支，我们称0z =为函数的多值性奇点.例1 函数()f z z =在平面上处处不可微.证 很显然()f z 在z 平面上处处连续.但 f z z z z z z z z z z z∆+∆-+∆-∆===∆∆∆∆, 当0z ∆→时,上式极限不存在.因为让z ∆取实数而趋于零时,其极限为1;z ∆取纯虚数而趋于零时,其极限为-1.例 2 试证:函数()nf z z = (n 为正整数)在z 平面上处处可微,且1nn dz nz dz -=. 证 设z 是随意固定的点,我们有12100()(1)lim lim[()]2n n n n n z z z z z n n nz z z z ---∆→∆→+∆--=+++∆∆ 1n nz -=.如函数()f z 在区域D 内处处可微,则称在区域D 内可微.2.函数解析的理论2.1 函数在区域D 内解析的定理定理2.4 函数()(,)(,)f z u x y iv x y =+在区域D 内解析的充要条件是:(1) 二元函数(,)u x y ,(,)v x y 在区域D 内可微;(2) (,)u x y ,(,)v x y 在D 内满足..C R -方程.例3 函数222()()(2)f z x y x i xy y =--+-在何处可导?何处解析?解 22()u x y x =--,2(2)v xy y =- 21u x x ∂=-∂, 2u y y∂=-∂,2v y x ∂=∂ ,22v x y y ∂=-∂. 上述偏导在平面上连续,令 u v x y∂∂=∂∂⇒21x -22x y =-,12y =. u v y x∂∂=-∂∂⇒2y -= 2y -故当且仅当12y =时, ..C R -条件成立,由定理知: ()f z 仅在直线12y =上可导.在直线12y =上,不存在某点的一个领域,使得()f z 在此领域上可导,故由解析的定义知: ()f z 在复平面内处处不解析.2.2函数在区域D 内解析的第一个等价定理定理3.15 函数()(,)(,)f z u x y iv x y =+在区域D 内解析的充要条件是:(1) x u , y u , x v y v 在D 内连续;(2) (,)u x y , (,)v x y 在D 内满足..C R -方程.证 充分性 即定理2.5,必要性 条件(2)的必要性已由定理2.1得出,现在由于解析函数()f z 的无穷可微性, ()f z '必在D 内连续,因而x u , y u , x v y v 必在D 内连续.例4 讨论函数2()||f z z =的解析性.解 因 22(,)u x y x y =+,(,)0v x y =,故 2x u x =,2y u y =,0x y v v ==.这四个偏导数在z 平面上处处连续,但只在0z =处满足..C R -方程,故函数只在0z =可微,从而,此函数在z 平面上处处不解析.例5 讨论函数2()f z x iy =-的可微性和解析性.解 因 2(,)u x y x =,(,)v x y y =-,故 2x u x =,0y u =,0x v =,1y v =-,所以 0y x u v ==-.要21x y u x v ===-,必须12x =-,故仅在直线12x =-上, ..C R -方程成立,且偏导数连续.从而仅在直线12x =-上可微,但在z 平面上, ()f z 却处处不解析. 注 上述两例,由于函数()f z 只在一个孤立点或只在一条直线上可微,各点都未形成由可微点构成的圆领域,故()f z 在其上都不解析,从而在z 平面上处处不解析.2.3 函数在区域D 内解析的第二个等价定理定理3.17 函数()f z 在区域G 内解析的充要条件是:(1)()f z 在G 内连续;(2) 对任一周线C ,只要C 及其内部全部含于G 内,就有()0cf z dz =⎰. 证 必要性可由柯西积分定理导出.至于充分性,我们可在G 内任一点0z 的一个领域k : 0||z ξρ-<来证明,只要ρ充分小,就知道()f z 在圆k 内解析,特别说来,在0z 解析,因为0z 可在G 内任意取,故()f z 在G 内解析.例6 如果函数()f z 为一整函数,且有使Re ()f z M <的实数M 存在,试证()f z 为常数.证 令()()f z F z e =,则()F z 为整函数.又在z 平面上Re ()|()|f z M F z e e =< ,故有界,由刘维尔定理可见()F z 是常数,因此()f z 也是常数.2.4函数在区域D 内解析的第三个等价定理()(,)(,f z u x y i v x y =+在区域D 内解析的充要条件是:在区域D 内(,)v x y 是(,)u x y 的共轭调和函数.例 7 验证32(,)3u x y x xy =-是z 平面上的调和函数,并求以(,)u x y 为实部的解析函数()f z ,使得(0)f i =.解 因在z 平面上任一点2233x u x y =-, 6y u xy =-, 6xx u x =, 6yy u x =-.故(,)u x y 在z 平面上为调和函数.解法一 由 x y y x dv v dx v dy u dx u dy =+=-+(,0)(,)2222(0,0)(,0)(,)6(33)6(33)x x y x v x y xydx x y dy xydx x y dy c ⇒=+-++-+⎰⎰220(33)y x y dy c =-+⎰ 233x y y c =-+,故 3223()3(3)f z u iv x xy i x y y c =+=-+-+33()x iy ic z ic =++++.要合 (0)f i =, 必1c =, 故3()f z z i =+.解法二 先由..C R -方程中的一个得 x y u v = 2233x y =-,由 x y y x dv v dx v dy u dx u dy =+=-+⇒ ()x v u dy x ϕ=+⎰故 233()v x y y x ϕ=-+,再由..C R -方程中的另一个得6()6x y v xy x u xy ϕ'=+=-=,故 ()0x ϕ'=,即 ()x ϕc =,因此 23(,)3v x y x y y c =-+. (下同解法一)例8 验证(,)arctan(0)y v x y x x=>在右半z 平面内是调和函数,并求以此为虚部的解析函数()f z . 解 222221x yy x v y x y x -==-++(0)x >, 2222211y x x v y x y x==++(0)x >,2222()xx xy v x y =+ , 2222()yy xy v x y =-+(0)x >, 于是 0xx yy v v +=(0)x >,故在右半z 平面内, (,)v x y 是调和函数.(,)()()x y u x y u dx y v dx y ϕϕ=+=+⎰⎰22221()ln()()2x dx y x y y x y ϕϕ=+=+++⎰,两端对求导得 222212()2y x y y y u v x y x y ϕ'⋅+==-=++,所以 ()0y ϕ'=,从而()y c ϕ= (任意常数),(,)u x y =221ln()2x y ++c , 故 ()f z =221ln()2x y c ++arctan (0)y i x x+> ln ||arg z i z c =++ln z c =+,它在右半z 平面内单值解析.2.5函数在区域D 内解析的第四个等价定理定理4.15 函数在区域内解析的充要条件为:在内任一点的领域内可展成的幂级数.例9 将1ze z-在0z =内展开成幂级数. 解 因1ze z-在||1z <内解析,故展开后的幂级数在||1z <内收敛. 已经知道 2312!3!zz z e z =++++ (||)z <+∞, 23111z z z z=++++- (||1)z <, 在||1z <时,将两式相乘得231111111(1)(1)(1)11!1!2!1!2!3!z e z z z z =++++++++++- . 例 10 试将函数()2z f z z =+按1z -的幂展开,并指明其收敛范围. 解 因()f z 是解析的,故2()1122(1)3z z f z z z z ==-=-++-+ 2111313z =-⋅-+ 0211(1)()33n n n z ∞=-=--∑ 1121()(1)333n nn z ∞==---∑ (|1|3)z -<. 结语 以上对在区域D 内解析的条件及应用做了简单归纳,由于复变函数主要讨论解析函数,因此判定一个函数是不是解析函数就十分重要.我们在学习的过程中,都要进行归纳总结,以便灵活运用.参考文献:[1] 复旦大学数学系.复变函数论[M ].上海:上海科学技术出版社,1987.[2] 陈方权 蒋绍惠.解析函数论基础[M ].北京:北京师范大学出版社,1987.[3] 钟玉泉.复变函数论(第三版)[M ].北京:高等教育出版社,2004.[4] 复变函数学习指导书. 北京: 高等教育出版社,1996.[5] 一个解析函数定理的推广.四川大学学报（自然科学版）,1990.。
