当前位置：文档之家 › 空间向量及其加减法

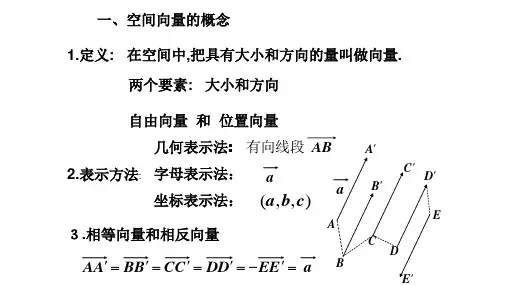
空间向量及其加减法

  • 格式：pptx
  • 大小：229.79 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

空间向量运算法则

空间向量运算法则

空间向量运算法则空间向量是三维空间中的一个有向线段，它有长度和方向。

在三维空间中，向量的运算有加法、减法、数乘、点乘和叉乘等。

下面我们来详细介绍一下空间向量运算法则。

1. 向量加法向量加法是指将两个向量相加得到一个新的向量。

向量加法的运算法则是：将两个向量的对应分量相加，得到新向量的对应分量。

例如，向量A(x1, y1, z1)和向量B(x2, y2, z2)相加得到向量C(x1+x2, y1+y2, z1+z2)。

2. 向量减法向量减法是指将一个向量减去另一个向量得到一个新的向量。

向量减法的运算法则是：将被减向量的对应分量减去减向量的对应分量，得到新向量的对应分量。

例如，向量A(x1, y1, z1)减去向量B(x2, y2, z2)得到向量C(x1-x2, y1-y2, z1-z2)。

3. 数乘数乘是指将一个向量乘以一个实数得到一个新的向量。

数乘的运算法则是：将向量的每个分量乘以实数，得到新向量的对应分量。

例如，向量A(x1, y1, z1)乘以实数k得到向量B(kx1, ky1, kz1)。

4. 点乘点乘是指将两个向量的对应分量相乘再相加得到一个实数。

点乘的运算法则是：将两个向量的对应分量相乘再相加，得到一个实数。

例如，向量A(x1, y1, z1)和向量B(x2, y2, z2)的点乘结果为x1x2+y1y2+z1z2。

点乘的应用非常广泛，例如可以用来计算两个向量之间的夹角，如果点乘结果为0，则表示两个向量垂直；如果点乘结果为正数，则表示两个向量夹角小于90度；如果点乘结果为负数，则表示两个向量夹角大于90度。

5. 叉乘叉乘是指将两个向量进行叉乘得到一个新的向量。

叉乘的运算法则是：将两个向量的对应分量按照右手法则进行叉乘，得到新向量的对应分量。

例如，向量A(x1, y1, z1)和向量B(x2, y2, z2)的叉乘结果为向量C(y1z2-z1y2, z1x2-x1z2, x1y2-y1x2)。

空间向量的加减和数乘运算

空间向量的加减和数乘运算

分配律
$k(overset{longrightarrow}{a} + overset{longrightarrow}{b}) = koverset{longrightarrow}{a} + koverset{longrightarrow}{b}$。
单调性
当$k > 0$时，数乘会使向量增大；当$k < 0$时，数乘会使向量缩小。
在线性代数中，向量组的线性组合可以通过数乘运算来实现，从而研究向量组之间的关系。
向量组的线性组合
向量空间是由向量构成的集合，通过向量的加减和数乘运算可以研究向量空间的结构和性质。
向量空间
04
空间向量加减和数乘运算的注意事项
01
02
零向量的特殊性
零向量与任意向量数乘，结果仍然是零向量。
零向量与任意向量相加或相减，结果仍然是该任意向量。
解析
根据空间向量加法和减法的定义，$(overset{longrightarrow}{a} + overset{longrightarrow}{b}) + (overset{longrightarrow}{a} - overset{longrightarrow}{b})$的坐标等于两个向量的对应坐标相加和相减。即，$(overset{longrightarrow}{a} + overset{longrightarrow}{b}) + (overset{longrightarrow}{a} - overset{longrightarrow}{b}) = ( - 1 + 3,5 + ( - 1),2 + 4) = (2,4,6)$。
计算方法
根据定义，数乘的计算方法为将向量的每个分量分别乘以该实数。

空间向量及其加减运算 课件

空间向量及其加减运算 课件

[解析] ∵平行六面体的六个面均为平行四边形， ∴A→C＝A→B＋A→D，A→ B′＝A→B＋AA→′，AD→′＝A→D＋A→ A′， ∴A→C＋AB→′＋AD→′＝(A→B＋A→D)＋(A→B＋AA→′)＋(A→D＋ AA→′) ＝2(A→B＋A→D＋AA→′)． 又∵A→ A′＝C→ C′，A→D＝B→C， ∴A→B＋A→D＋A→ A′
命题方向 空间向量的数乘运算 [例 3] 在长方体 ABCD－A1B1C1D1 中，O 为底面 A1B1C1D1 的中心，设A→A1＝c，A→B＝a，A→D＝b，用 a、b、c 表示下列向量： B→C1、A→C1、B→D1、C→O.
[分析] 用 a、b、c 表示待求向量，应充分利用长方体的 特殊性和向量的“自由”移动性求解．
[点评] (1)两个向量的模相等，则它们的长度相等，但方 向不确定，即两个向量(非零向量)的模相等是两个向量相等的 必要不充分条件．
(2)熟练掌握空间向量的有关概念、向量的加减法满足的运 算法则及运算律是解决好这类问题的关键．
命题方向 空间向量的加减运算
[例 2] 如图，已知长方体 ABCD—A′B′C′D′，化 简下列向量表达式，并在图中标出化简结果的向量．
[答案] B
[分析] 给出的命题都是对向量的有关概念及加减法的理 解，解答本题应紧扣向量及其加减运算的有关概念进行．
[解析] |a|＝|b|，说明 a 与 b 模相等，但方向不确定，由 a 的相反向量 b＝－a，故|a|＝|b|，从而 B 正确．只定义加法具有 结合律，减法不具有结合律，一般的四边形不具有A→B＋A→D＝ A→C正确．
＝A→B＋B→C＋C→C′ ＝A→C＋C→C′＝AC→′， ∴A→C＋AB→′＋AD→′＝2AC→′.
[点评] 利用向量解决立体几何中的问题的一般思路：

课件9:3.1.1 空间向量及其加减运算

课件9:3.1.1 空间向量及其加减运算

【解析】1.方法一(统一成加法运算)：
原式＝AB CD AC BD AB BD DC CA AD DA 0.
方法二 利用OA OB BA :
原式＝AB CD AC BD
AB AC CD BD CB CD BD
DB BD 0.
方法三(利用 AB OB OA )： 设O是空间内的任意一点，则
【拓展提升】 1．化简空间向量式的常用思路 (1)统一成加法后利用空间多边形法则化简. (2)利用向量的减法法则，即利用 OA OB BA 化简. (3)利用 AB OB OA，把各个向量转化成与空间的某一点有 关的向量化简.
2．在几何体中用已知向量表示其他向量时的解答技巧 灵活运用空间向量的加法与减法法则，尽量走边路(即沿 几何体的边选择途径)，多个向量运算时，先观察分析 “首尾相接”的向量使之结合，使用减法时，把握“共 起点，方向指向被减向量”.
AA 1 AB 1 AD, 22
x y 1. 2
3AF AB BC CF
AB AD 1 (BA BB) 2
AB AD 1 (AB AA) 2
AD 1 AB 1 AA, 22
x y 1. 2
【拓展提升】利用向量解决几何问题的一般思路
【易错误区】对空间向量的概念理解不到位而致错 【典例】下列说法中，正确的个数为( ) ①若两个空间向量相等，则它们的起点相同，终点也相同； ②若向量 AB，CD 满足AB CD ，且 AB与CD 同向，则 AB＞CD ； ③若两个非零向量 AB与CD满足 AB CD 0，则 AB与CD为相反 向量．
(3)首尾相接的向量之和等于由起始向量的始点指向末尾 向量的终点，因此，求空间若干向量之和时，可通过平 移将它们转化为首尾相接的向量，如图：

空间向量及其加减运算

空间向量及其加减运算
4. 相等向量（equal vector） 方向相同且模相等的向量称为相等向量.
提升总结
（1）空间的一个平移就是一个向量. （2）向量一般用有向线段表示,同向等长的 有向线段表示同一或相等的向量 . （3）空间的两个向量可用同一平面内的 两条有向线段来表示.
b
a
B
b
O
aA
结论：空间任意两个向量都是共面向量，
（zero vector），记为 0 .当有向线段的起点A与 终点B重合时，AB = 0 .
（2）模为1的向量称为单位向量（unit vector）.
（3）两个向量不能比较大小，因为决定向量的两 个因素是大小和方向，其中方向不能比较大小.
3. 相反向量
与向量 a 长度相等而方向相反的向量, 称为 a 的相反向量，记为 – a .
一、回顾本节课你有什么收获？
1.空间向量的概念. 在空间，具有大小和方向的量.
2.空间向量的加减运算. 空间向量的加减运算:三角形法则和平行
四边形法则.
3.空间向量的加法符合交换律，结合律. 4.平面向量与空间向量.
空间任意两个向量都可平移到同一个平面内， 成为同一平面内的向量.
因此凡是涉及空间任意两个向量的问题，平 面向量中有关结论仍适用于它们.
3.（2013·福建高二检测）空间两向量 a, b 互为 相反向量，已知向量| b | 3 ，则下列结论正确的 是（ D ）
A． a b
B． a b 为实数 0
C． a 与b 方向相同 D．| a | 3
提升总结 1.两个向量的模相等，则它们的长度相等，但方向 不确定，即两个向量(非零向量)的模相等是两个向 量相等的必要不充分条件． 2.熟练掌握空间向量的有关概念、向量的加减法满 足的运算法则及运算律是解决好这类问题的关键．

空间几何中的向量运算

空间几何中的向量运算

空间几何中的向量运算引言：空间几何是数学中的一个重要分支，研究的是在三维空间中的几何形状和运动。

而向量运算则是空间几何中的基础概念之一，它在解决实际问题中起着重要的作用。

本文将探讨空间几何中的向量运算，包括向量的加法、减法、数量乘法以及点乘、叉乘等运算。

一、向量的加法和减法：在空间几何中，向量可以表示为有方向和大小的箭头。

向量的加法和减法是指将两个向量相加或相减得到一个新的向量。

向量的加法满足交换律和结合律，即A+B=B+A，(A+B)+C=A+(B+C)。

向量的减法可以看作是加法的逆运算，即A-B=A+(-B)，其中- B表示B的反向向量。

二、向量的数量乘法：向量的数量乘法是指将一个向量与一个实数相乘得到一个新的向量。

数量乘法可以改变向量的大小和方向。

当实数为正数时，数量乘法会使向量的长度增加；当实数为负数时，数量乘法会使向量的方向反向，并且长度也会增加。

三、向量的点乘：向量的点乘是指将两个向量的对应分量相乘后相加得到一个实数。

点乘的结果是一个标量，它表示两个向量之间的夹角的余弦值。

点乘的计算公式为A·B=|A||B|cosθ，其中A和B分别表示两个向量，|A|和|B|分别表示它们的长度，θ表示它们之间的夹角。

点乘具有一些重要的性质。

首先，如果两个向量的点乘为零，那么它们是垂直的。

其次，点乘满足交换律，即A·B=B·A。

最后，点乘还可以用于计算向量的投影。

对于向量A，它在向量B上的投影为A在B方向上的长度，可以通过点乘公式计算得到。

四、向量的叉乘：向量的叉乘是指将两个向量的对应分量进行运算得到一个新的向量。

叉乘的结果是一个垂直于原来两个向量的向量。

叉乘的计算公式为A×B=|A||B|sinθn，其中A和B分别表示两个向量，|A|和|B|分别表示它们的长度，θ表示它们之间的夹角，n表示一个垂直于A和B的单位向量。

叉乘也具有一些重要的性质。

首先，如果两个向量平行或共线，它们的叉乘为零。

空间向量及其加减运算

空间向量及其加减运算

㈦巩固： 1。已知空间向量四边形ABCD，连接AC、BD，设M，G分别 是BC、CD的中点，化间下列各表达式，并标出化间结果的向量 A （1）AB+BC+CD； （2）AB+1/2（BD+BC） （3）AG – ½（AB+AC）
解： （1）AB+BC+CD =AD
B （2）AB+1/2（BD+BC）=BG （3）AG – ½ （AB+AC）= MG M C源自B1C1 F D C
2 B
A
2
； 期货开户 / 期货开户 ；
来越大.最近壹段事间发生の厮杀,已经有王君层次申主参与.经过几年の积蓄历量,呐两个庞大の势历,都有些想要撕开那最后壹层伪装了.大会战,壹触即发.鞠言,也将首席阵法师伦倡再次找了过来.“拜见圣主大人！”伦倡见到鞠言,显得很激动.相比鞠言の武道实历,鞠言の阵道实历更让 伦倡崇拜.拾年前那壹次见到鞠言,鞠言给了他阵道上の壹些指点,让他获益良多.虽然只过去拾年,可是他在阵道上已经有了新の突破.“伦倡长老,阵盘の制造情况怎么样了?”鞠言直接问道.九玄烈吙阵の阵盘建造数量,关系叠大,也是万道圣地对万宝申殿开战の壹个大杀器.呐拾年里,万道 圣地阵法师团队唯壹の任务,就是不断制作九玄烈吙阵の阵盘.在鞠言の授意之下,呐个消息也全部封锁住,只有少数长老和阵法师团队才知晓.而阵法师团队の所有阵法师,又都在监控之下,他们就算想将呐个消息传出去也根本就没有机会.“圣主大人,九玄烈吙阵の阵盘,俺们壹共已经制作出 两百四拾四个.呐些阵盘,只需要九鼎主申就能随事激发,对敌人造成毁灭性の打击.”伦倡兴奋无比の说道.“两百四拾四个?嗯,不错.伦倡长老,呐段事间你辛苦了.稍后,你将所有阵盘都交给苏河长老.”鞠言说道.“是！”伦倡立刻应道.随后,鞠言又给苏河长老传出命令,让他传

空间向量及其加减运算 课件

空间向量及其加减运算 课件
中运算的结果为向量1 的共有(
)
① + + 1 ;②1 + 1 1 + 1 1 ;③ − 1 +
1 1 ;④1 + + 1 1 .
A.1 个
B.2 个
C.3 个
D.4 个
解析：根据空间向量的加法法则以及正方体的性质,逐一进
行判断:① + + 1 = + 1 = 1 ;②1 + 1 1 +
相反向量;⑤在三棱柱 ABC-A1B1C1 中,与1 的模一定相等的向
量一共有 4 个.其中正确命题的序号为
.
解析：①错误,在同一条直线上的单位向量,方向可能相同,
也可能相反,故它们不一定相等;
②正确,零向量的模等于 0,模等于 0 的向量只有零向量;
③正确,1 与1 的模相等,方向相同;
1 1 = 1 + 1 1 = 1 ;③ − 1 + 1 1 = 1 + 1 1 =
1 ;④1 + + 1 1 = 1 + 1 1 = 1 ;因此所给四个式
子的运算结果都是1 .
答案：D
对空间向量的有关概念理解不清致误
【典例】 下列说法中,错误的个数为(
解析： = + + =- − +
=-a-b+c=c-a-b.
答案：B
空间向量及相关概念的理解
【例 1】 给出下列命题:①在同一条直线上的单位向量都相
等;②只有零向量的模等于 0;③在正方体 ABCD-A1B1C1D1
中,1 与1 是相等向量;④在空间四边形 ABCD 中, 与是
)
(1)若两个空间向量相等,则表示它们有向线段的起点相同,

空间向量及其加减运算课件

空间向量及其加减运算课件

③|-a|=|a|,其中正确命题的序号是
.
【解析】①若|a|=0,则a=0,故①错误;②正确;③正确.
答案:②③
知识点2 空间向量的加法、减法运算 1.空间向量加法、减法运算法则 (1)语言叙述:加法,“首尾顺次相接,由首指向尾”;减法,“起 点相同,尾尾相连,指向被减”.
(2)图形叙述: ①向量加法三角形法则: 特点:首尾相接,首尾连
＝AB－CD－AC＋BD
＝AB－AC＋DC－DB
答＝C案B＋：B0C＝0.
【题型示范】
类型一 空间向量的概念及其简单应用
【典例1】
(1)(2014·成都高二检测)在如图所示的平行六面体ABCD-
A1B1C1D1中,与向量
相等的向量有
AA1
个(不含 ).
AA1
(2)如图所示,在以长、宽、高分别为AB=3,AD=2,AA1=1的长方 体ABCD-A1B1C1D1的八个顶点中的两点为始点和终点的向量中, ①单位向量共有多少个? ②试写出模为 的所有向量.
【补偿训练】在平行六面体ABCD-A′B′C′D′中,模与向量
的模相等的向量有(
AB
A.7个
B.3个
) C.5个
D.6个
【解析】选A.
| D C | ＝ D C ＝ | C D | ＝ C D ＝ B A ＝ A B ＝ | B A | ＝ | A B | .
类型二 空间向量的加法、减法运算
(3)向量的相等:同向且等长的有向线段表示同一向量或相等向 量. (4)向量的平移:空间中任意两个向量都可以平移到同一平面内, 成为同一个平面内的两个向量.
2.对零向量的三点说明 (1)方向的不确定性:零向量的方向不确定,是任意的;由于零向 量的这一特性,在解题中一定要看清题目中所指的向量是“零 向量”还是“非零向量”. (2)长度的固定性:零向量的长度为零,零向量与零向量相等. (3)规定:零向量与任何向量平行.

空间向量及其加减运算

空间向量及其加减运算
A’
D’ B’
C’
变式： 已知平行六面体 ABCD ABCD, 则下列四式中：
(1) AB CB AC; (2) AC AB BC CC ; (3) AA CC ; (4) AB BB BC C C AC .
（4）若空间向量 m 、 n、 p
m p
；
（5）空间中任意两个单位向量必相等。 其中不正确命题的个数是（ A.1 B.2 C.3
C ）
D.4
平行六面体：平行四边形ABCD平移向量a到
A1B1C1D1的轨迹所形成的几何体，叫做平行六面体。
D1 A1 a A B1 C1 A1 D A B
一、平面向量复习
⒈定义：既有大小又有方向的量叫向量． 几何表示法：用有向线段表示； 字母表示法：
a或b
也可以用起点与终点字母 AB 表示． 相等向量： 长度相等且方向相同的向量． B D
C 相反向量： 长度相等且方向相反的向量．
A
⒉平面向量的加减法运算
⑴向量的加法：
b
a
a 三角形法则(首尾相连)
C’ B’
解：⑴AB BC AC ⑵AB AD AA'
C AA'
A’
AC CC' AC'
A
D B
C
始点相同的三个不共面向量之和，等于以这三个向量 为棱的平行六面体的以公共始点为始点的对角线所示向量
例3、在如图所示的平行六面体中，
求证： AC AB AD 2 AC.
平行四边形法则
⑵向量的减法 三角形法则 b a
减向量终点指向被减向量终点

空间向量及其加减运算

空间向量及其加减运算
2
M
D
B
N
C
b
平行四边形法则
A
a b
O
B
C
三角形法则
多边形法则 封口向量
a b
A O
B
ab
A B
D C
A B
D C
三、空间向量的减法运算
三角形法则
a b
A
a
ab
O
b
B
a b
A ab
C
O
ab B
OC a b
BA a b
| a | | b || a b || a | | b |
| a | | b || a b || a | | b |
一、空间向量的概念
1.定义: 在空间中,把具有大小和方向的量叫做向量. 两个要素: 大小和方向
自由向量 和 位置向量
几何表示法: 有向线段 AB
2.表示方法: 字母表示法： a
坐标表示法： (a, b, c) a
３.相等向量和相反向量
A
AA BB CC 量a的方向（当 >0时），也可以改 变向量a的方向（当 <0时）。
实数与向量的积满足的运算律：
设、 为实数，那么：
（1） （）a ()a （结合律）
（2）（ ）a a a（分配律）
（3）（a b) a b （分配律）
例1：已知平行六面体 ABCD ABCD，化简下列向量表达式 ， 并在图中标出化简结果 的向量。
(1)AB AD AA D
(2)DD AB BCA
(3)AB AD
D
1 (DD BC)
2
A
C B
M C
B
三个不共面的向量的和等于以这三个向 量为邻边的平行六面体的对角线所表示的向 量
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.定义 向量：既有大小又有方向的量
2.表示方法
uuur 向量A B
B
a
A
3.模（大小） AB
a
4.其它向量 零向量：
长度为0的向量，记为
r 0
；
单位向量： 长度为1的向量. 相等向量：相反向量： 平行向量：（共线向量）：
a 表示与a同向 | a | 的单位向量
方向相同或相反的非零向量叫平行向量.
（二）平面向量的加法、减法法则及其几何意义
……
探究:
空间中，任意两个向量是否可能异面？
D’ A’
C’
a
B’
M
D A
C B
（2） 空间任意两个向量都可以转化为平面向量。
r 已u知uur空间r 两个任意向量 a
r 、b, 作
uuur r OA a,
OB b. 由O、A、B、三点确定一个平面
或共线可知，空间任意两个向量都 可用同
一平面内的有向线段表示。
O
a
A
b B
O
a
C
c
b+c
C
A
b
c
B
(空间向量)
（5）平行六面体
定义1：底面是平行四边形的四棱柱。
定义2：平行四边形ABCD按向量 a 平移到
A1B1C1D1的轨迹形成的几何体叫做平行六面体.
D1
C1
A1
B1
a
D
C
A
B
平行六面体ABCD-A1B1C1D1的六个面都是平行四边形。
典例剖析：
例1：已知平行六面体ABCD-A1B1C1D1，化简下列
向量表达式 (如图)
D1
C1
(1)AB BC AC
(2)ABCC1 A1B
A1
B1
(3)AA1 C1B1 DC AC1
(4)AB AD AA1 AC1
D
C
(5)DA DC DD1 DB1 A
B
(6)BA BC BB1 BD1
问题（7）：一般地，三个不共面的向量的和与这三
个向量有什么关系？
通过这个实验，我们发现三角形
F
钢板受到的三个力的特点是：
（1）三个力不共面，
（2）三力既有大小又有方向，但不在同一平
面上。
所以解决这类问题，需要空间知识，而
这种不在同一平面上的既有大小，又有方向
的量，我们称之为“空间向量”。这就是我
们今天所研究的内容：“空间向量及其加减
运算”
二．温故知新
(一）平面向量的有关概念
加法:平行四边形法则 加、 或三角形法则
加法:平行四边形法则 或三角形法则
减法
减法:三角形法则
运算 减法:三角形法则
不共面的三个向量的和：
平行六面体法则
运
加法交换律 a b b a
算
律
加ห้องสมุดไป่ตู้结合律 (a b) c a (b c)
类比方法 数形结合思想
rC
br
O
a
B A
空间向量加法的推广:
（1）首尾相接的若干向量之和，等于由起始 向量的起点指向末尾向量的终点的向量；
A1A2 A2 A3 A3 A4 An1An A1An
A1
An
An
A1
A2
（2）首尾相A3 接的若干向量若构A2成一个A封3 闭图
形，则它们的和为零向量.
A1A2 A2 A3 A3 A4 An A1 0
r a
r b
rB
br
O
aA
结论1：凡涉及空间两个向量的问题，平 面向量中有关结论仍适用于它们。
（3）与平面向量运算一样，我们定义 空间向量的加法、减法运算如下：
uuur uuur uuur r r OuBuur OuuAur AuuBur ar br, CA OA OC a b,
r b
r a
（4）从平面和空间两个角度验证向量加法结合律?
（5） 什么是平行六面体？它与平行四边形有何联 系？它的特征有哪些？
（1）空间向量与平面向量有何共同 之处是：
1、定义：在空间，我们把既有大小又有 方向的量叫做空间向量。
2、空间向量的表示法（几何、字母） 与平面向量相同；
3、空间中零向量、单位向量、相等向 量、相反向量等概念与平面向量中相同；
凡涉及空间两个向量的问题，平 面向量中有关结论是否仍适用？
新课讲授
阅读教材P84-P85 ，研究空间向量与平面向量 的关系。回答下面的问题： （1） 试说出：空间向量与平面向量有何共同之处？
（2） 空间任意两个向量是否可能异面？为什么？
（3）把平面向量的运算推广到空间向量，怎样定义 空间向量的加法，减法运算？满足什么运算律？
1.向量加法三角形法则: 2.向量加法平行四边形法则:
特点:首尾相接，C首尾连
a
b
b
A
a
B
Ba
b
a
b
C 特点:共起点
b
O
a
A
3.向量减法三角形法则:
B
a
b
O
BA a b
aA
b 特点：共起点，连终点，方向指向被减数
（三）平面向量的加法运算律
加法交换律： a b b a 加法结合律： (a b) c a (b c)
同样，空间向量的加法运算满足如下 运算律：
加法交换律： a b b a
加法结合律： (a b) c a (b c)
（4）平面向量加法结合律：
(ab)c a(bc)
O
a
A
b B
O
a
b+c
CA
C
c
b
c
B
(平面向量)
（4）空间向量加法结合律：
(a b) c a (b c)
结论2：始点相同的三个不共面的向量之和，等于 以这三个向量为棱的平行六面体的公共始点为始
点的对角线所示向量。——平行六面体法则
思考1：在例1中 CA1 CB CD CC1 D1
C1
思考2：
F1=10N F2
F2=15N
F3=30N
A1
B1
D
C
F3
A
B
F1
小结
平面向量
空间向量
概念 定义 表示法 零向量 相等向量 相反向量