平面向量的实际背景及基本概念

姓名，年级：时间：2．1 平面向量的实际背景及基本概念[教材研读]预习课本P74～76，思考以下问题1．向量是如何定义的?向量与数量有什么区别？2．怎样表示向量？向量的相关概念有哪些?3．两个向量（向量的模）能否比较大小？4．零向量与单位向量有什么特殊性？0与0的含义有什么区别? 5．如何判断相等向量或共线向量?向量错误!与向量错误!是相等向量吗？［要点梳理］1．向量的概念和表示方法（1)概念：既有大小，又有方向的量称为向量．(2)向量的表示2.向量的长度（或称模）与特殊向量（1)向量的长度(或模)定义：向量的大小叫做向量的长度(或模）．（2)向量的长度表示：向量错误!,a的长度分别记作：|错误!|，|a｜。

(3）特殊向量：①长度为0的向量为零向量，记作0；②长度等于1个单位的向量，叫做单位向量．3．向量间的关系（1）相等向量：长度相等且方向相同的向量，叫做相等向量,记作:a ＝b。

（2)平行向量：方向相同或相反的非零向量，也叫共线向量；a平行于b，记作a∥b；规定零向量与任一向量平行．［自我诊断]判断(正确的打“√"，错误的打“×”)1．两个向量能比较大小．（)2．向量的模是一个正实数．（)3．单位向量的模都相等．( ）4．向量错误!与向量错误!是相等向量．( )［答案］1。

×2。

× 3.√ 4.×错误!思考：已知下列各量:①力；②功；③速度；④质量；⑤温度；⑥位移;⑦加速度；⑧重力;⑨路程;⑩密度．其中是数量的有__________，是向量的有__________．提示:②④⑤⑨⑩①③⑥⑦⑧下列说法正确的有__________．（填序号)①若｜a|＝｜b|，则a与b的长度相等且方向相同或相反；②若|a｜＝｜b|，且a与b的方向相同，则a＝b；③由于0方向不确定，故0不能与任意向量平行；④向量a与向量b平行,则向量a与b方向相同或相反；⑤起点不同,但方向相同且模相等的向量是相等向量．［思路导引] 利用向量的有关概念逐一判断．[解析] ①不正确．由|a|＝｜b|只能判断两向量长度相等,不能确定它们方向的关系．②正确．因为|a｜＝｜b｜，且a与b同向，由两向量相等的条件,可得a＝b.③不正确．依据规定：0与任一向量平行．④不正确．因为向量a与向量b若有一个是零向量，则其方向不定．⑤正确．对于一个向量只要不改变其大小与方向，是可以任意移动的．[答案] ②⑤解决与向量概念有关问题的方法解决与向量概念有关题目的关键是突出向量的核心——方向和长度,如:共线向量的核心是方向相同或相反,长度没有限制；相等向量的核心是方向相同且长度相等；单位向量的核心是方向没有限制，但长度都是一个单位长度；零向量的核心是方向没有限制，长度是0;规定零向量与任一向量共线．只有紧紧抓住概念的核心才能顺利解决与向量概念有关的问题．［跟踪训练]下列说法错误的有__________．（填上你认为所有符合的序号)①两个单位向量不可能平行；②两个非零向量平行，则它们所在直线平行;③当两个向量a，b共线且方向相同时，若｜a｜〉｜b｜，则a>b.[解析］①错误，单位向量也可以平行；②错误，两个非零向量平行，则它们所在直线还可能重合；③错误，两个向量是不能比较大小的，只有模可以比较大小．[答案] ①②③错误!思考：向量就是有向线段，这种说法对吗？提示:不对，向量与有向线段是两个不同的概念，可以用有向线段表示向量．在如图所示的坐标纸上（每个小方格边长为1）,用直尺和圆规画出下列向量:（1）错误!,使|错误!|＝4错误!，点A在点O北偏东45°；（2)错误!，使｜错误!|＝4，点B在点A正东；（3)错误!，使｜错误!|＝6，点C在点B北偏东30°。

考纲（理）：平面向量：（1）平面向量的实际背景及基本概念①了解向量的实际背景。

②理解平面向量的概念，理解两个向量相等的含义。

③理解向量的几何表示。

（2）向量的线性运算①掌握向量的加法、减法的运算，并理解其几何意义。

②掌握向量数乘的运算及其意义，理解两个向量共线的含义。

③了解向量线性运算的性质及其几何意义。

（3）平面向量的基本定理及坐标表示①了解平面向量的基本定理及其意义②掌握平面向量的正交分解及其坐标表示③会用坐标表示平面向量的加法、减法与数乘运算④理解用坐标表示的平面向量共线的条件。

（4）平面向量的数量积①理解平面向量数量积的含义及其物理意义②了解平面向量的数量积与向量投影的关系③掌握数量积的坐标表达式，会进行平面向量数量积的运算④能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系。

（5）向量的应用①会用向量方法解决某些简单的平面几何问题②会用向量方法解决简单的力学问题与其他一些实际问题空间向量与立体几何（1）空间向量及其运算①了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示。

②掌握空间向量的线性运算及其坐标表示。

③掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线与垂直。

（2）空间向量的应用①理解直线的方向向量与平面的法向量。

②能用向量语言表述直线与直线、直线与平面、平面与平面的垂直和平行关系③能用向量方法证明有关直线和平面位置关系的一些定理（包括三垂线定理）④能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题，了解向量方法在研究立体几何问题中的作用。

线性规划：二元一次不等式组与简单线性规划问题①会从实际情境中抽象出二元一次不等式组。

②了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组。

③会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决。

文科：平面向量（1）平面向量的实际背景及基本概念①了解向量的实际背景。

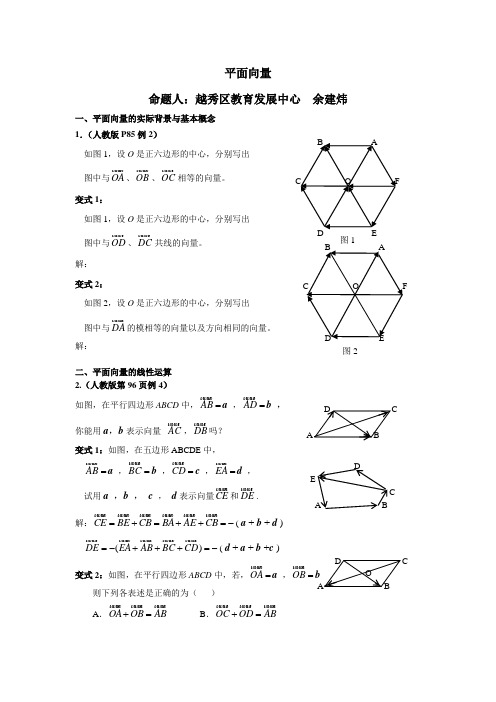
平面向量命题人：越秀区教育发展中心 余建炜一、平面向量的实际背景与基本概念 1．（人教版P85例2）如图1，设O 是正六边形的中心，分别写出 图中与OA 、OB 、OC 相等的向量。

变式1：如图1，设O 是正六边形的中心，分别写出 图中与OD 、DC 共线的向量。

解： 变式2：如图2，设O 是正六边形的中心，分别写出 图中与DA 的模相等的向量以及方向相同的向量。

解：二、平面向量的线性运算 2.（人教版第96页例4）如图，在平行四边形ABCD 中，AB =a ，AD =b ， 你能用a ，b 表示向量 AC ，DB 吗？ 变式1：如图，在五边形ABCDE 中，AB =a ，BC =b ，CD =c ，EA =d ，试用a ，b ， c ， d 表示向量CE 和DE . 解：CE BE CB BA AE CB =+=++=-( a + b + d )()DE EA AB BC CD =-+++=-( d + a + b +c )变式2：如图，在平行四边形ABCD 中，若，OA =a ，OB =b则下列各表述是正确的为（ ）A ．OA OB AB += B ．OC OD AB +=D EC A BC BAC O FD E图1图2C ．CD =-a + b D ．BC =-(a + b ) 正确答案：选D变式3：已知=a ，=b, =c ,=d , 且四边形ABCD 为平行四边形，则（ ）A. a +b +c +d =0B. a －b +c －d =0C. a +b －c －d =0D. a －b －c +d =0正确答案：选A变式4：在四边形ABCD 中，若12AB CD =-，则此四边形是( )A ．平行四边形B ．菱形C ．梯形D ．矩形 正确答案：选C变式5：已知a 、b 是非零向量，则|a |=|b |是(a +b )与(a －b )垂直的 （ ）A ．充分但不必要条件 BC ．充要条件D ．既不充分也不必要条件正确答案：选C变式6：在四边形ABCD 中，=a +2b ，=－4a －b ，=－5a －3b ，其中a 、b 不共线，则四边形ABCD 为（ ） A.平行四边形 B.矩形C.梯形D.菱形【解析】 ∵AD =CD BC AB ++=－8a －2b =2BC ，∴BC AD //.∴四边形ABCD 为梯形. 正确答案：选C变式7：已知菱形ABCD ，点P 在对角线AC 上（不包括端点A 、C ），则等于（ ） A.λ(+),λ∈(0,1)B.λ(+),λ∈(0,22) C.λ(－),λ∈(0,1)D.λ(-),λ∈(0,22)【解析】 由向量的运算法则AC =AB +AD ，而点P 在对角线AC 上，所以AP 与AC 同向，且||＜||,∴=λ(+),λ∈(0,1).正确答案：选 A变式8：已知D 、E 、F 分别是△ABC 的边BC 、CA 、AB 的中点，且=a ，=b ，=c ,则下列各式： ①EF =21c －21b ②BE =a +21b ③=－21a +21b ④++=0其中正确的等式的个数为（ ）A.1B.2C.3D.4正确答案：选B 3．（人教版第98页例6）如图，已知任意两个非零向量a 、b ，试作OA =a + b ，OB =a + 2b ， OC =a + 3b ，你能判断A 、B 、C 三点之间的位置关系吗？为什么？变式1：已知OA =a + 2b ，OB =2a + 4b ，OC =3a + 6b (其中a 、b 是两个任意非零向量) ，证明：A 、B 、C 三点共线．证明：∵AB OB OA =-=a + 2b ，AC OC OA =-=2a + 4b ，∴ 2AC AB = 所以，A 、B 、C 三点共线．变式2：已知点A 、B 、C 在同一直线上，并且OA =a + b ，(2)OB m =- a + 2b ，(1)OC n =+ a + 3b (其中a 、b 是两个任意非零向量) ，试求m 、n 之间的关系．解：(3)AB OB OA m =-=- a + b ，AC OC OA n =-= a + 2b 由A 、B 、C 三点在同一直线上可设AB k AC =，则 (3)21m kn k -=⎧⎨=⎩ 所以 1(3)2m n -= 即 260m n --=为所求．4．（人教版第102页第13题）已知四边形ABCD ，点E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，求证：EF HG = 变式1：已知任意四边形ABCD 的边AD 和BC 的中点分别为E 、F ，求证：2AB DC EF +=.证明：如图，连接EB 和EC ， 由EA AB EB +=和EF FB EB +=可得，EA AB EF FB +=+ （1） 由ED DC EC +=和EF FC EC +=可得，ED DC EF FC +=+ （2） （1）+（2）得， 2EA ED AB DC EF FB FC +++=++ （3） ∵E 、F 分别为AD 和BC 的中点，∴0EA ED +=，0FB FC +=， 代入（3）式得，2AB DC EF +=ba三、平面向量的基本定理及坐标表示 2.（人教版第109页例6）已知a = (4，2)，b = (6，y )，且a // b ，求 y ． 变式1：与向量a = (12，5) 平行的单位向量为（ ）A ．1251313⎛⎫⎪⎝⎭，- B ．1251313⎛⎫- ⎪⎝⎭，-C ．1251313⎛⎫⎪⎝⎭， 或1251313⎛⎫- ⎪⎝⎭，- D ．1251313⎛⎫- ⎪⎝⎭， 或1251313⎛⎫ ⎪⎝⎭，-正确答案：选C变式2：已知a (1,2)=，b (),1x =，当a +2b 与2a －b 共线时，x 值为 （ ）A ．1B ．2C ．13D ．12正确答案：选D变式3：已知A (0,3) 、B (2,0) 、C (－1,3) 与AC AB 2+方向相反的单位向量是( )A ．(0,1)B ．(0,－1)C ． (－1,1)D ．(1,－1) 正确答案：选A变式4：已知a = (1，0)，b = (2，1) ．试问：当k 为何实数时， k a －b 与a +3b 平行, 平行时它们是同向还是反向？ 解：因为 k a －b ()21k =--，，a +3b ()73=，．由已知得，()3270k -+= 解得 13k =-，此时，k a －b 713⎛⎫=-- ⎪⎝⎭，，a +3b ()73=，，二者方向相反． 2.（人教版第110页例8）设点P 是线段12PP 上的一点，1P 、2P 的坐标分别为()11y x ，，()22y x ，． (1) 当点P 是线段12PP 上的中点时，求点P 的坐标； (2) 当点P 是线段12PP 的一个三等分点时，求P 的坐标 变式1：已知两点()3,2M ，()5,5N --，12MP MN =，则P 点坐标是 （ ）A ．()8,1-B ．31,2⎛⎫-- ⎪⎝⎭ C ．31,2⎛⎫ ⎪⎝⎭D ．()8,1- 正确答案：选B变式2：如图，设点P 、Q 是线段AB 的三等分点， 若OA ＝a ，OB ＝b ，则OP ＝2133+a b ， OQ ＝1233+a b (用a 、b 表示)四、平面向量的数量积 5．（人教版第116页例3）已知|a |＝6，|b | ＝4且a 与b 的夹角为60︒，求 (a + 2b)·(a 3-b ) ． 变式1：已知()()3,4,223,a b a ba b ==++=那么a 与b 夹角为A 、60︒B 、90︒C 、120︒D 、150︒正确答案：选C变式2：已知向量a 和b 的夹角为60°，| a | ＝ 3，| b | ＝ 4，则（2a – b ）·a 等于 （A ）15 （B ）12 （C ）6 （D ）3 正确答案：选B变式3：在△ABC 中，已知||=4，||=1，S △ABC =3，则·等于（ ）A.－2B.2C.±2D.±4 正确答案：选C变式4：设向量2172e e t +与向量21e t e +的夹角为钝角，求实数t 的取值范围. 解：∵0))(72(2121<++e t e e e t ，故071522<++t t ，解之217-<<-t ． 另有λλt t ==7,2，解之14,214-=-=λt ， ∴)21,214()214,7(--⋃--∈t ．2.（人教版第116页例4）已知|a |＝3，|b | ＝4且a 与b 不共线，k 为何实数时，向量a + k b 与a k -b 互相垂直？ 变式1：已知a ⊥b ，|a |＝2，|b | ＝3，且向量3a + 2b 与k a -b 互相垂直，则k 的值为（ ）A ．32-B ．32C ．32± D ．1 正确答案：选B变式2：已知|a |＝1，|b | ＝2且（a －b ）⊥a ，则a 与b 夹角的大小为 45º ． 解：2.（人教版第119页 第11题）已知a = (4，2)，求与向量a 垂直的单位向量的坐标． 变式1：若i = (1,0), j =(0,1)，则与2i +3j 垂直的向量是 ( )A ．3i +2jB ．－2i +3jC ．－3i +2jD ．2i －3j正确答案：选C变式2：已知向量)1,1(=a ，)3,2(-=b ，若b a k 2-与a 垂直，则实数k =（ ）A ．1B ．－1C ．0D ．2正确答案：选B变式3：若非零向量,互相垂直，则下列各式中一定成立的是 （ ）A ．b a b a -=+B ．||||b a b a -=+C ．0))((=-+D ．0)(2=-b a正确答案：选B变式4：已知向量a ＝（3，－4），b ＝（2，x ）， c ＝（2，y ）且a ∥b ，a ⊥c ．求|b －c |的值． 解：∵ a ∥b ，∴ 3x ＋8＝0． ∴x ＝38-． ∴ b ＝（2， 38-） ． ∵ a ⊥c ， ∴ 6－4y ＝0． ∴ y ＝23． ∴ c ＝（2， 23）．而b －c ＝（2，38-）－（2，23）＝（0，－256），∴ |b －c |＝256．（人教版第118页例5）已知A (1，2)，B (2，3)，C (2-，5)，试判断ABC ∆的形状，并给出证明．变式1：O 是ABC ∆所在的平面内的一点，且满足()()0OB OC OC OA -⋅-=，则ABC ∆ 一定为（ ）A ．正三角形B ．等腰直角三角形C ．直角三角形D ．斜三角形 正确答案：选C变式2：已知A 、B 、C 三点不共线，O 是△ABC 内的一点，若＋＋＝0，则O 是△ABC 的（ ）A ． 重心B ． 垂心C ． 内心D ． 外心正确答案：选A变式3：已知02=+⋅，则△ABC 一定是 （ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰直角三角形正确答案：选B变式4：四边形ABCD 中，)3,2(),,(),1,6(--===y x （1）若//，试求x 与y 满足的关系式；（2）满足（1）的同时又有⊥，求y x ,的值及四边形ABCD 的面积。

2.1平面向量的实际背景及基本概念一、选择题1.【题文】下列各量中不是向量的是（ ） A ．浮力 B ．风速 C ．位移D ．密度2．【题文】在下列判断中，正确的是( )①长度为的向量都是零向量；②零向量的方向都是相同的；③单位向量的长度都相等； ④单位向量都是同方向；⑤任意向量与零向量都共线． A ．①②③ B ．②③④ C ．①②⑤ D ．①③⑤3．【题文】若AB AD =且BA CD =，则四边形ABCD 的形状为（ ） A ．平行四边形 B ．矩形 C ．菱形 D ．等腰梯形4．【题文】已知：如图，D ，E ，F 依次是等边三角形ABC 的边AB ，BC ，CA 的中点，在以A ，B ，C ，D ，E ，F 为起点或终点的向量中，与向量AD 共线的向量有（）A ．个B ．个C ．个D ．个5．【题文】下列说法正确的有( )①方向相同的向量叫相等向量；②零向量的长度为；③共线向量是在同一条直线上的向量；④零向量是没有方向的向量；⑤共线向量不一定相等；⑥平行向量方向相同． A ．个 B ．个 C ．个 D ．个6．【题文】给出下列说法：①AB 和BA 的模相等；②方向不同的两个向量一定不平行；③向量就是有向线段；④0=0；⑤AB CD >，其中正确说法的个数是( )A. B. C. D.7．【题文】若四边形ABCD 是矩形，则下列说法中不正确的是 （ ） A ．AB 与CD 共线B ．AC 与BD 共线C ．AD 与CB 是相反向量 D ．AB 与CD 的模相等8.【题文】下列说法正确的是( )A ．有向线段AB 与BA 表示同一向量 B ．两个有公共终点的向量是平行向量C ．零向量与单位向量是平行向量D ．对任一向量，aa是一个单位向量 二、填空题9．【题文】如图，正六边形ABCDEF 中，点O 为中心，以,,,,,,A B C D E F O 为起点与终点的向量中，与向量AB 平行的向量有个（含AB ）．10.【题文】给出下列四个条件：①=a b ；②=a b ；③与的方向相反；④0=a 或0=b ，其中能使a b 成立的条件有________．11．【题文】下列说法中，正确的是 ． ①向量AB 的长度与BA 的长度相等；②向量a与向量b平行，则a与b的方向相同或相反；③两个有共同起点的单位向量，其终点必相同；④向量AB与向量CD是相等向量，则A、B、C、D能构成平行四边形．三、解答题12．【题文】如图，D，E，F分别是△ABC的边AB，BC，CA的中点，在以A，B，C，D，E，F为起点和终点的向量中：（1）找出与向量EF相等的向量；（2）找出与向量DF相等的向量．13．【题文】如图，在△ABC中，D，E分别是边AB，AC的中点，F，G分别是DB，EC 的中点，求证：向量DE与FG共线．14．【题文】如图，EF是△ABC的中位线，AD是BC边上的中线，在以A，B，C，D，E，F为端点的有向线段表示的向量中请分别写出：（1）与向量CD共线的向量；（2）与向量DF的模相等的向量；（3）与向量DE相等的向量.2.1平面向量的实际背景及基本概念参考答案与解析一、选择题1.【答案】D【解析】根据向量的定义，从大小和方向两个方面考虑，可知密度不是向量．考点：平面向量的概念.【题型】选择题【难度】较易2．【答案】D【解析】由零向量与单位向量的概念知①③⑤正确．考点：零向量与单位向量.【题型】选择题【难度】较易3．【答案】C【解析】四边形ABCD中，∵BA CD=，∴BA CD，且BA CD=，∴四边形ABCD是平行四边形.又AB AD=，∴平行四边形ABCD是菱形.考点：相等向量.【题型】选择题【难度】较易4．【答案】C【解析】∵D，E，F分别为AB，BC，CA的中点，∴AD∥EF ，∴与向量AD共线的向量有AB，FE，EF，DA，BA，BD，DB，共7个．考点：共线向量.【题型】选择题【难度】较易5．【答案】A【解析】长度相等且方向相同的向量叫做相等向量，故①错误；长度为的向量叫零向量，故②正确；通过平移能够移到同一条直线上的向量叫共线向量，故③错误；零向量的方向是任意的，故④错误；共线向量方向相同或相反，⑤正确；平行向量方向相同或相反，故⑥错误，因此②与⑤正确，其余都是错误的，故选C.考点：相等向量，共线向量.【题型】选择题【难度】一般6．【答案】B【解析】①正确，AB与BA是方向相反、模相等的两个向量；②错误，方向不同包括共线反向的向量；③错误，向量用有向线段表示，但二者并不等同；④错误，是一个向量，而为一数量，应为0=0；⑤错误，向量不能比较大小.只有①正确，故选B.考点：向量的有关概念.【题型】选择题【难度】一般7．【答案】B【解析】∵四边形ABCD是矩形，∴AB CD且AB CD=，AD CB，∴AB 与CD共线，且模相等，AD与CB是相反向量，∵AC与BD相交，∴AC与BD不共线，故B错误.考点：共线向量，相等向量.【题型】选择题【难度】一般 8. 【答案】C【解析】向量AB 与BA 方向相反，不是同一向量；有公共终点的向量的方向不一定相同或相反；当=0a 时，aa无意义，故A 、B 、D 错误．零向量与任何向量都是平行向量，C 正确．考点：平行向量;单位向量. 【题型】选择题 【难度】较难二、填空题 9． 【答案】10【解析】正六边形ABCDEF 中，点O 为中心，以,,,,,,A B C D E F O 为起点与终点的向量中，与向量AB 平行的向量有,,,,,,,,,AB BA OC CO OF FO CF FC DE ED ，共10个． 考点：平行向量. 【题型】填空题 【难度】较易 10.【答案】①③④【解析】因为与为相等向量，所以a b ，即①能够使a b 成立；=a b 并没有确定与的方向，即②不能够使ab 成立；与方向相反时，a b ，即③能够使a b 成立；因为零向量与任意向量共线，所以0=a 或0=b 时，a b 能够成立．故使a b 成立的条件是①③④.考点：平行向量. 【题型】填空题 【难度】一般11． 【答案】①【解析】对于①，向量AB 与BA 互为相反向量，长度相等，正确；对于②，因为零向量与任何向量平行，但零向量的方向是任意的，不能说方向相同或相反，所以②错误；对于③，两个有共同起点的单位向量，其终点不一定相同，因为方向不一定相同，所以③错误； 对于④，向量AB 与向量CD 是相等向量，则A 、B 、C 、D 可能在同一直线上，则A 、B 、C 、D 四点不一定能构成平行四边形，所以④错误．综上，正确的是①． 考点：平面向量的概念. 【题型】填空题 【难度】一般三、解答题 12．【答案】（1）,BD DA （2）,BE EC【解析】（1）∵E ，F 分别为BC ，AC 的中点， ∴EFBA ，且12EF BA =，又D 是BA 的中点， ∴EF BD DA ==，∴与向量EF 相等的向量是,BD DA .（2）∵D ，F 分别为BA ，AC 的中点， ∴DFBC ，且12DF BC =， 又E 是BC 的中点，∴DF BE EC ==， ∴与向量DF 相等的向量是,BE EC ． 考点：共线向量.【题型】解答题【难度】较易13．【答案】详见解析【解析】证明：∵D，E分别是边AB，AC的中点，∴DE是△ABC的中位线，∴DE BC，∴四边形DBCE是梯形．又∵F，G分别是DB，EC的中点，∴FG是梯形DBCE的中位线，∴FG DE.∴向量DE与FG共线．考点：向量共线.【题型】解答题【难度】一般14．【答案】（1）,,,,,,BD BC EF DB CB FE DC（2）,,,,FD AE EA EB BE（3）,CF FA【解析】根据三角形中位线的性质及共线向量及相等向量的概念即可得到：（1）与向量CD共线的向量为,,,,,,BD BC EF DB CB FE DC．（2）与向量DF的模相等的向量为,,,,FD AE EA EB BE．（3）与向量DE相等的向量为,CF FA．考点：相等向量，平行向量. 【题型】解答题【难度】一般。

第二章第一节平面向量的实际背景及基本概念1．丰富多彩的背景，引人入胜的内容．教材首先从力、位移等量讲清向量的实际背景以及研究向量的必要性，接着介绍了平面向量的有关知识．学生将了解向量丰富的实际背景，理解平面向量及其运算的意义，能用向量语言与方法表述和解决数学、物理中的一些问题，发展运算能力和解决实际问题的能力．平面向量基本定理是平面向量正交分解及坐标表示的基础，从学生熟知的功的概念出发，引出了平面向量数量积的概念及其几何意义，接着介绍了向量数量积的性质、运算律及坐标表示．向量数量积把向量的长度和三角函数联系了起来，这样为解决有关的几何问题提供了方便，特别能有效地解决线段的垂直问题．最后介绍了平面向量的应用．2．教学的最佳契机，全新的思维视角．向量具有几何形式和代数形式的“双重身份”，这一概念是由物理学和工程技术抽象出来的．反过来，向量的理论和方法，又成为解决物理学和工程技术的重要工具，向量之所以有用，关键是它具有一套良好的运算性质，通过向量可把空间图形的性质转化为向量的运算，这样通过向量就能较容易地研究空间的直线和平面的各种有关问题．这一章的内容虽然概念多，但大都有其物理上的来源，虽然抽象，却与图形有着密切的联系，向量应用的优越性也是非常明显的．全新的思维视角，恰当的教与学，使得向量不仅生动有趣，而且是培养学生创新精神与能力的极佳契机．3．本章充分体现出新教材特点．以学生已有的物理知识和几何内容为背景，直观介绍向量的内容，注重向量运算与数的运算的对比，特别注意知识的发生过程．对概念、法则、公式、定理等的处理主要通过观察、比较、分析、综合、抽象、概括得出结论．这一章中的一些例题，教科书不是先给出解法，而是先进行分析，探索出解题思路，再给出解法．解题后有的还总结出解决该题时运用的数学思想和数学方法，有的还让学生进一步考虑相关的问题．对知识的处理，都尽量设计成让学生自己观察、比较、猜想、分析、归纳、类比、想象、抽象、概括的形式，从而培养学生的思维能力．向量的坐标实际上是把点与数联系起来，进而可把曲线与方程联系起来，这样就可用代数方程研究几何问题，同时也可以用几何的观点处理某些代数问题．4作者：赵勇，永安三中教师，本教学设计获福建省教学设计大赛三等奖整体设计教学理念新的课程标准要求我们创造性地使用教材，积极开发、利用各种教学资源，创设教学情境，让学生通过主动参与、积极思考、合作交流和创新等过程，获得知识、能力、情感的全面发展．本节课将充分体现以“学生为本”的教学观念，实现课程理念、教学方式和学生学习方式的转变．教学目标1．通过力的分析等实例，了解向量的实际背景；理解向量的概念．2．理解向量的几何表示；掌握零向量、单位向量、平行向量等概念；3．理解相等向量和共线向量等概念，并会辨认图形中的相等向量或作出与某一已知向量的相等向量．教学重点、难点1．通过学生自主探究，并在教师的引导下，使学生理解向量的概念、相等向量的概念、向量的几何表示等是本节课的重点．2．难点是学生对向量的概念和共线向量的概念的理解．学情和教材分析《向量》是高中数学新教材必修四第二章第1节．向量是近代数学中重要和基本的概念之一，有深刻的几何背景，是解决几何问题的有力工具．向量概念引入后，全等和平行(平移)、相似、垂直、勾股定理就可转化为向量的加(减)法、数乘向量、数量积运算，从而把图形的基本性质转化为向量的运算体系．向量是沟通代数、几何与三角函数的一种工具，有着极其丰富的实际背景，在数学和物理学科中具有广泛的应用．所以，向量是高考必考的重点内容，又因为其抽象性，它还是学生在学习中的一个难学内容．本节内容是向量一章的第一节课，因此，是十分关键、重要的一节课．教学准备多媒体课件教学过程导入新课位置是几何学研究的重要内容之一，几何中常用点表示位置，研究如何由一点的位置确定另外一点的位置．如图1，如何由点A确定点B的位置？图1一种常用的方法是，以A为参照点，用B点A点之间的方位和距离确定B点的位置．如，B点在A点东偏南45°，30千米处．这样，在A点与B点之间，我们可以用有向线段AB表示B点相对于A点的位置．有向线段AB就是A点与B点之间的位移．位移简明地表示了位置之间的相对关系．像位移这种既有大小又有方向的量，加以抽象，就是我们本章要研究的向量．推进新课新知探究本章引言中，我们知道，位移是既有大小，又有方向的量，你还能举出一些这样的量吗？图2请大家阅读课本2.1.1向量的物理背景与概念；2.1.2向量的几何表示．并回答下面问题： (1)什么是向量？向量和数量有何不同？ (2)向量如何表示？(3)什么是零向量和单位向量？ (4)什么是平行向量？待学生阅读完后，老师总结并展示课件： 1．什么是向量？向量和数量有何不同？(数量：只有大小，没有方向的量) 在质量、重力、速度、加速度、身高、面积、体积这些量中，哪些是数量？哪些是向量？ 数量有：质量、身高、面积、体积 向量有：重力、速度、加速度提问：角度，海拔，温度是向量吗？ 2．向量如何表示？(1)几何表示——向量常用有向线段表示：有向线段的长度表示向量的大小，箭头所指的方向表示向量的方向．图3 注：以A 为起点，B 为终点的有向线段记为AB →，线段AB 的长度记作|AB →|(读为模)； (2)也可以表示为a ，b ，c ，…，大小记作：|a|、|b|、|c |、…说明一：我们所说的向量，与起点无关，用有向线段表示向量时，起点可以取任意位置．所以数学中的向量也叫自由向量．如图4：它们都表示同一个向量．图4练习：向量AB →和BA →是同一个向量吗？为什么？ 不是，方向不同．探究：向量就是有向线段吗？有向线段就是向量吗？ 说明二：有向线段与向量的区别： 有向线段：有固定起点、大小、方向．向量：可选任意点作为向量的起点、有大小、有方向．图5有向线段AB →、CD →是不同的．图6向量AB →、CD →是同一个向量． 3．什么是零向量和单位向量？零向量：长度为0的向量，记为0； 单位向量：长度为1的向量．注：零向量，单位向量都是只限制大小，不确定方向的． 向量之间的关系： 4．什么是平行向量？方向相同或相反的非零向量叫平行向量． 注：1.若是两个平行向量，则记为a ∥b .2．我们规定，零向量与任一向量平行，即对任意向量a ，都有0∥a . 练习：判断下列各组向量是否平行？图7向量的平行与线段的平行有什么区别？ 练习：已知下列命题：(1)向量AB →和向量BA →长度相等；(2)方向不同的两个向量一定不平行；(3)向量就是有向线段；(4)向量0＝0；(5)向量AB →大于向量CD →.其中正确命题的个数是( )A ．0B ．1C ．2D ．3 答案：B例1试根据图8中的比例尺以及三地的位置，在图中分别用向量表示A 地至B 、C 两地的位移，并求出A 地至B 、C 两地的实际距离(精确到1 km)．图8请同学们阅读课本2.1.3相等向量与共线向量，并回答问题：什么是相等向量和共线向量？待学生回答后，老师总结并展示课件： 5．什么是相等向量和共线向量？长度相等且方向相同的向量叫相等向量．a ＝b ＝c A 1B 1→＝A 2B 2→＝A 3B 3→＝A 4B 4→图9注：1.若向量a ，b 相等，则记为a ＝b ；2．任意两个相等的非零向量，都可用同一条有向线段来表示，并且与有向线段的起点无关．平行向量也叫共线向量．注：任一组平行向量都可以平移到同一直线上． 练习：判断下列命题是否正确：(1)两个向量相等，则它们的起点相同，终点相同；(2)若|a|＝|b |，则a ＝b ；(3)若AB →＝DC →，则四边形ABCD 是平行四边形；(4)平行四边形ABCD 中，一定有AB →＝DC →；(5)若m ＝n ，n ＝k ，则m ＝k ；(6)若a ∥b ，b ∥c ，则a ∥c .其中不正确命题的个数是( )A ．2B ．3C ．4D ．5 答案：C练习：下列说法正确的是( ) A ．若|a|>|b|，则a>b B ．若|a |＝0，则a ＝0C ．若|a|＝|b|，则a ＝b 或a ＝－bD ．若a ∥b ，则a ＝bE ．若a ＝b ，则|a|＝|b |F ．若a ≠b ，则a 与b 不是共线向量G ．若a ＝0，则－a ＝0 答案：EG例2如图10，设O 是正六边形ABCDEF 的中心，分别写出图中与OA →、OB →、OC →相等的向量．图10解：OA →＝CB →＝DO →， OB →＝DC →＝EO →， OC →＝AB →＝ED →＝FO →.练习：如图11，EF 是△ABC 的中位线，AD 是BC 边上的中线，在以A 、B 、C 、D 、E 、F 为端点的有向线段表示的向量中请分别写出：图11(1)与向量CD →共线的向量有________个，分别是________________________________；(2)与向量DF →的模一定相等的向量有________个，分别是______________________；(3)与向量DE →相等的向量有________个，分别是__________．答案：(1)7 DC →、DB →、BD →、FE →、EF →、CB →、BC → (2)5 FD →、EB →、BE →、EA →、AE →(3)2 CF →、FA →课堂小结 通过本节课的学习，要求大家能够理解向量的概念；掌握向量的几何表示；理解零向量、单位向量、平行向量、相等向量等概念，并能进行简单的应用．作业习题2.1A 组2,5设计思路1．首先先对本节课教材内容进行分析2．教材内容的安排和处理根据我所教学生的特点，我对教材进行了如下处理，先由物理中的位置关系导入新课，然后提出问题，并要求学生带着问题去阅读课本，最后由老师总结，并对概念进行概念辨析，以加大学生的思维的深度，拓宽了学生的视野，实现本节课难点的突破，整堂课充分发挥学生的主导作用．3．教法“问题是数学的灵魂，也是学好数学的必然手段”，本节课总体上以问题串的形式，设计为七问五练．着重抓四个知识点，突出学生的“主导地位”．并通过多媒体课件的演示，直观展示向量的有关内容，激发学生的兴趣．4．学法指导以问题为载体，通过提问、阅读、归纳，练习的过程，掌握思考、讨论、交流的学习方法，并体验探究和发现的乐趣．。