简单的超静定问题

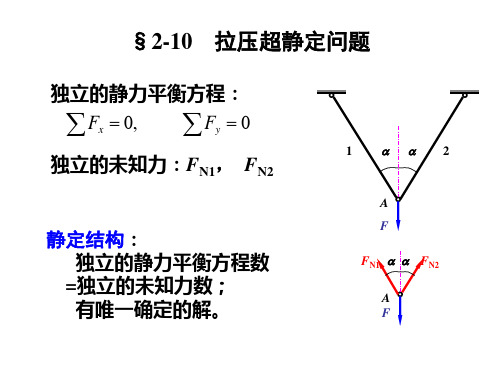
第六章简单的超静定问题知识要点1．超静定问题的概念（1）静定问题结构或结构的约束反力或内力均能通过静力学平衡方程求解的问题。

（2）超静定问题结构或构件的约束反力或内力不能仅凭静力学平衡方程全部求解的问题。

（3）超静定次数未知力(约束反力或内力)数超过独立的静力平衡方程书的数目。

（4）多余约束力超静定问题中，多余维持静力平衡所必需的约束（支座或杆件）。

（5）多余未知力与多余（支座或杆件）相应的支座反力或内力。

（6）基本静定系在求解静定结构时，解除多余约束，并代之以多余未知力，从而得到一个作用有荷载和多余未知力的静定结构，称之为原超静定结构的基本体静定系。

2．静不定问题的解题步骤（1） 静力平衡条件——利用静力学平衡条件，列出平衡方程。

（2） 变形相容条件——根据结构或杆间变形后应保持连续的变形相容条件，作出位移图，由位移图的几何关系列出变形间的关系方程。

（3） 物理关系——应用胡克定律列出力与变形间的关系方程。

（4） 将物理关系代入变形相容条件，得补充方程 。

补充方程和静力平衡方程，二者方程数之和正好等于未知数的个数，联立平衡方程和补充方程，求解全部未知数。

习题详解6-1 试作题6-1图（a ）所示等直杆的轴力图。

解 解除题6-1图（a ）所示等直杆的约束，代之以约束反力，作受力图，如题6-1图（b ）所示。

由静力学平衡条件,03,0=-+=∑F F F F B A Y和变形协调条件0=∆+∆+∆DB CD AC 并将()EAa F EA a F F EA a F B DB A CD A AC -=∆-=∆=∆,22,代入式②，可得 联立式①，③，解得45,47F F F F B A == 轴力如图6-1图（c ）所示6-2 题6-2图（a ）所示支架承受荷载F=10 kN,1,2,3各杆由同一材料制成，其横截面面积分别为232221200,150,100mm A mm A mm A ===。

试求各杆的轴力。

解 这是一个超静定问题，铰链A 的受力图，如题6-2图（c ）所示。

利用静力学平衡条件列平衡方程0301230cos 330cos ,0N N N x F F F F =+=∑ F F F FN N y =+=∑030130sin 30sin ,0 变形的几何关系如题6-2图（b ）所示,变形协调条件为03020130sin 30tan 230sin l l l ∆+∆=∆ 应用胡克定律，三杆的变形为1l ∆=33332222111,,EA l F l EA l F l EA l F N N N =∆=∆ 代入③，得补充方程 033302222011130sin 30tan 230sin EA l F EA l F l EA l F N N N +=∆= 联立式①，②，④，解得各杆的轴力分别为kN F kN F kN F N N N 55.11,68.2,45.8321===6-3 一刚性板有四根支柱支撑，四根支柱的长度和截面都相同，如 题6-3图（a ）所示。

如果荷载F 作用在A 点，试求这四根支柱各受力多少。

解 这是一个超静定问题，对题6-3图（b ）所示刚性板的受力图列静力学平衡方程F F F F F N N N N =+++432142342122322N N N N N N F F e a F e F F e a F =⎪⎪⎭⎫ ⎝⎛-=++⎪⎪⎭⎫ ⎝⎛+ 由6-3图（b ）所示变形几何关系，并注意到42l l ∆=∆，得1l ∆+232l l ∆=∆应用胡克定律，得四根柱的变形1l ∆=EA l F l EA lF l EA lF l EA lF N N N N 4433221,,,=∆=∆=∆代入④，得补充方程2312N N N F F F =+联立式①，②，③，⑤，解得各柱的内力分别为4,241,4,2414321F F F a e F F F F a e F N N N N =⎪⎭⎫ ⎝⎛+==⎪⎭⎫ ⎝⎛-= 6-4 刚性杆AB 的左端铰支，两根长度相等，横截面面积相同的钢杆CD 和EF 使该刚性杆处于水平位置，如题6-4图（a ）所示。

如已知F=50kN,两根钢杆的横截面面积A=10002mm ，试求两杆的轴力和应力。

解 这是一个超静定问题，解除题6-4图（a ）所示结构 D ，F 处的约束，代之以约束反力，作受力图，如题6-4图（b ）。

其静力学平衡方程为aF a F a F MN N A 32,021=+=∑ 变形协调条件为1l ∆=22l ∆应用胡克定律，可得两杆的变形1l ∆=EA l F lEA lF N N 221,=∆代入式②，得补充方程21N N F F =联立式①，③，解得两杆的内力分别为kN F kN F N N 60,3021==两杆的应力分别为Pa A F Pa A F N N 6322631110100010601010001030--⨯⨯==⨯⨯==σσ6-5题6-5图（a ）所示刚性梁受均布荷载作用，梁在A 端铰支，在B 点和C 点由两根钢杆B D 和CE 支承。

已知钢杆B D 和CE 的横截面面积2122400200mm A mm A ==和，钢的许用应力[]σ=170MPa ，试求该钢杆的强度。

解 这是一个超静定问题，解除梁AB 在C ，B 处的约束，代之以约束反力，作受力图，如题6-5图（b ）所示。

其静力学平衡条件为2213302131,0⨯⨯=⨯+⨯=∑N N A F F M变形协调条件为 3121=∆∆l l 应用胡克定律，得,111EA l F l N =∆ l EA F l N 8.1222⨯=∆ 代入式②，得补充方程212.1N N F F =联立式①，③，解得各杆的内力分别为N F N 5.381=，N F N 322=各杆的应力分别为[][]MPa MPa Pa A F MPa MPa Pa A F N N 1701601020010321709610400105.3863226311==⨯⨯====⨯⨯==--σσσσ故钢杆安全6-6 试求题6-6图（a ）所示结构的许可荷载[]F 。

已知杆AD,CE,BF 的横截面面积均为A ，杆材料的许用应力为[]σ，梁AB 可视为刚体。

解 这是一个超静定问题，受力图如题6-6图（b ）所示。

其静力学平衡条件为,0=∑y F F F F F N N N =++321变形协调条件为1l ∆=2l ∆=3l ∆应用胡克定律，可得各杆的伸长 ,111EA l F l N =∆ EAl F l EA l F l N N 333222,=∆=∆ 代入式③，得补充方程3212N N N F F F ==联立式①，②，④，解得各杆的内力分别为 5,52,52321F F F F F F N N N === 由杆1或杆2的强度条件 []σσσ≤==AF N 121 得[][]A F σ5.21≤由杆3的强度条件 []σσ≤=A F N 33 得[][]A F σ5.23≤比较[]1F 和[]3F ，所以结构的许可荷载为[][]A F σ5.2≤6-7 横截面为250mm ⨯250mm 的短木柱，用四根40 mm ⨯40mm ⨯5mm 的等边角钢加固，并承受压力F ，如题6-7图（a ）所示。

已知角钢的许用应力[]s σ=160MPa ，弹性模量GPa E W 10=。

试求短木柱的许可荷载[]F 。

解 查文献1中型钢表，可得40 mm ⨯40 mm ⨯5mm 的等边角钢的截面面积2791.3cm A S =。

受力图如题6-7图（b ）所示。

这是一次超静定问题。

其静力学平衡条件为,0=∑y F F F F Nw Ns =+木柱与角钢的变形协调条件为w s l l ∆=∆由胡克定律确定角钢和木柱的变形 ww w Nw w s s s Ns s A E l F l A E l F l =∆=∆,1 代入式②，得 294925.010*******.31020041⨯⨯=⨯⨯⨯⨯⨯-Nw Ns F F联立式①，③，解得角钢和木柱承受的轴力F F F F Nw Ns 673.0,372.0==由角钢的强度条件 MPa F A F s Ns s 16010791.34327.044≤⨯⨯==-σ 得[]kN F 742≤由木柱的强度条件 MPa F A F w Nw w 1225.0673.02≤==σ 得 []kN F 1114≤比较以上所得的两种许可荷载，选用[]kN F 742=6-8 水平刚性横梁AB 上部由杆1和杆2悬挂，下部由角支座C 支撑，如题6-8图（a ）所示。

由于制造误差，杆1的长度少量了mm 5.1=δ。

已知两杆的材料和横截面面积均相等，且A A A GPa E E E =====2121,200。

试求装配后两杆的应力。

解 这是个装配应力问题。

受力如题6-8图（b ）所示其静力学平衡条件为,0=∑c M 145sin 2021⨯=⨯N N F F装配后的变形几何关系如题6-8图（c ）所示，其变形协条件为245cos021=∆∆-llδ应用胡克定律确定杆1和杆2的变形,111EAlFl N=∆EAlFl N222=∆代入式②，得补充方程2114NNFFlEA=-δ联立式①，③，并注意到122ll=可得各杆的内力分别为()()12822,128121+=+=lEAFlEAFNNδδ所以各杆的应力分别为()()()()MPaPalEAFMPaPalEAFNN9.451285.1105.11020022128222.161285.1105.1102001283912239111=+⨯⨯⨯⨯⨯=+===+⨯⨯⨯⨯=+==--δσδσ6-9 题6-9图（a）所示阶梯状杆，其上端固定，下端与支座距离mm1=δ。

已知上，下两段杆的横截面面积分别为6002mm 和3002mm ，材料的弹性模量GPa E 210=。

试作题6-9图（a ）所示荷载作用下杆的轴力图。

解 这是一个超静定问题，受力图如题6-9图（b ）所示。

其静力学平衡条件为,0=∑y F 4060+=+B A F F变形协调条件为δ=∆+∆+∆CB DC AD l l l应用胡克定律，确定各杆段的变形(),,60,2111EA l F l EA l F l EA l F l CB B CB DC A DC AD A AD -=∆-=∆=∆ 并代入式②，得补充方程2704.26.3=-B A F F解得联立式①，③，kN F kN F B A 15,85==作轴力图，如题6-9图（c ）所示6-10 两端固定的阶梯状杆如题6-10图（a ）所示。

已知AC 段和BD 的横截面面积为A ，CD 段的横截面面积为2A ；杆材料的弹性模量为GPa E 210=，线膨胀系数106)(1012--⨯=C l α 。