下载文档原格式
晶面指数计算公式晶面指数是晶体学中用来描述晶面方向的重要概念，而晶面指数的计算公式则是我们理解和确定晶面的关键工具。
在晶体结构中，晶面是由一系列原子排列所构成的平面。
为了准确地描述这些晶面在空间中的取向，我们就需要用到晶面指数。
晶面指数的计算其实有一套相对固定的方法。
首先，我们要找出晶面在三个坐标轴上的截距。
这可不是随便找的哦，得是实实在在的数值。
比如说，一个晶面在 X、Y、Z 轴上的截距分别是 2a、3b、4c（这里的 a、b、c 是晶格常数）。
接下来，就要进行倒数计算啦。
把这些截距的数值取倒数，就得到1/2、1/3、1/4 。
但是还没完呢，我们还得把这些倒数化作互质的整数。
怎么化呢？就是将它们分别乘以它们分母的最小公倍数。
在这个例子里，最小公倍数是 12 ，所以经过计算后，得到 6、4、3 。
最后，把这组整数括在圆括号里，就得到了这个晶面的指数(643) 。
我还记得之前给学生们讲这个知识点的时候，有个小调皮鬼一直搞不明白为啥要这么算。
我就给他打了个比方，我说这就好比咱们分蛋糕。
晶面就像是蛋糕的切面，坐标轴就是切蛋糕的刀，截距就是每一刀下去切到的位置。
而计算晶面指数呢，就是把这些切的位置给规范化，方便咱们统一描述和交流。
那孩子听了之后，眼睛一下子亮了起来，好像突然就开窍了。
从那以后，每次遇到晶面指数的计算，他都特别积极，还能给其他同学讲明白呢。
在实际的研究和应用中，晶面指数的准确计算对于理解晶体的物理和化学性质都有着至关重要的作用。
比如说，不同的晶面可能具有不同的表面能，这会影响晶体的生长过程和形态。
总之，晶面指数计算公式虽然看起来有点复杂，但只要我们掌握了方法，多做几道练习题，就一定能轻松拿下它。
相信大家在今后的学习和研究中，都能熟练运用这个工具，去探索晶体世界的奥秘！。
晶向指数和晶面指数例题晶向指数和晶面指数是晶体学中非常基础的概念，它们用于描述晶体内部的结构和性质。
在本文中，我们将通过几个例题来介绍晶向指数和晶面指数的概念和应用。
一、晶向指数晶向指数是用来表示晶体中某个方向的指标，通常用方向余弦表示。
举个例子，假设有一个晶体，其晶格常数为a，b，c，那么其晶向指数(hkl)表示为：(hkl) = (h/a, k/b, l/c)其中h，k，l是整数，表示晶体中某个方向的坐标。
这个晶向指数(hkl)表示的是晶体中从原点出发，经过(h, k, l)个晶格常数所到达的点的位置。
下面是一个例题：例1：一个简单立方晶体，其晶格常数为a，求以下晶向的晶向指数：（1）[100]；（2）[110]；（3）[111]。
解：（1）[100]方向的晶向指数为(1, 0, 0)；（2）[110]方向的晶向指数为(1, 1, 0)；（3）[111]方向的晶向指数为(1, 1, 1)。
二、晶面指数晶面指数是用来表示晶体中某个晶面的指标，通常用晶面法向量的坐标表示。
举个例子，假设有一个晶体，其晶格常数为a，b，c，那么其晶面指数(hkl)表示为：(hkl) = [h, k, l]其中h，k，l是整数，表示晶面法向量的坐标。
这个晶面指数(hkl)表示的是晶体中法向量的坐标。
下面是一个例题：例2：一个简单立方晶体，其晶格常数为a，求以下晶面的晶面指数：（1）(100)；（2）(110)；（3）(111)。
解：（1）(100)晶面的晶面指数为[1, 0, 0]；（2）(110)晶面的晶面指数为[1, 1, 0]；（3）(111)晶面的晶面指数为[1, 1, 1]。
三、晶向指数和晶面指数的应用晶向指数和晶面指数在晶体学中有着重要的应用。
举个例子，它们可以用于描述晶体中的晶面间距、晶体的晶体学性质等。
下面是一个例题：例3：一个简单立方晶体，其晶格常数为a，试判断以下晶向是否相等：（1）[100]和[010]；（2）[110]和[1-10]；（3）[111]和[1-1-1]。
1.4 晶向指数和晶面指数一晶向和晶面1 晶向晶向：空间点阵中各阵点列的方向（连接点阵中任意结点列的直线方向）。
晶体中的某些方向，涉及到晶体中原子的位置，原子列方向，表示的是一组相互平行、方向一致的直线的指向。
2 晶面晶面：通过空间点阵中任意一组阵点的平面（在点阵中由结点构成的平面）。
晶体中原子所构成的平面。
不同的晶面和晶向具有不同的原子排列和不同的取向。
材料的许多性质和行为（如各种物理性质、力学行为、相变、X光和电子衍射特性等）都和晶面、晶向有密切的关系。
所以，为了研究和描述材料的性质和行为，首先就要设法表征晶面和晶向。
为了便于确定和区别晶体中不同方位的晶向和晶面，国际上通用密勒（Miller）指数来统一标定晶向指数与晶面指数。
二晶向指数和晶面指数的确定1 晶向指数的确定方法三指数表示晶向指数[uvw]的步骤如图1所示。
(1)建立以晶轴a，b，c为坐标轴的坐标系，各轴上的坐标长度单位分别是晶胞边长a，b，c，坐标原点在待标晶向上。
(2)选取该晶向上原点以外的任一点P(xa，yb，zc)。
(3)将xa，yb，zc化成最小的简单整数比u，v，w，且u∶v∶w = xa∶yb∶zc。
(4)将u，v，w三数置于方括号内就得到晶向指数[uvw]。
图1 晶向指数的确定方法图2 不同的晶向及其指数当然，在确定晶向指数时，坐标原点不一定非选取在晶向上不可。
若原点不在待标晶向上，那就需要选取该晶向上两点的坐标P(x1，y1，z1)和Q(x2，y2，z2)，然后将(x1-x2)，(y1-y2)，(z 1-z 2)三个数化成最小的简单整数u ，v ，w ，并使之满足u ∶v ∶w =(x 1-x 2)∶(y 1-y 2)∶(z 1-z 2)。
则[uvw ]为该晶向的指数。
显然，晶向指数表示了所有相互平行、方向一致的晶向。
若所指的方向相反，则晶向指数的数字相同，但符号相反，如图3中[001]与[010]。
说明： a 指数意义：代表相互平行、方向一致的所有晶向。
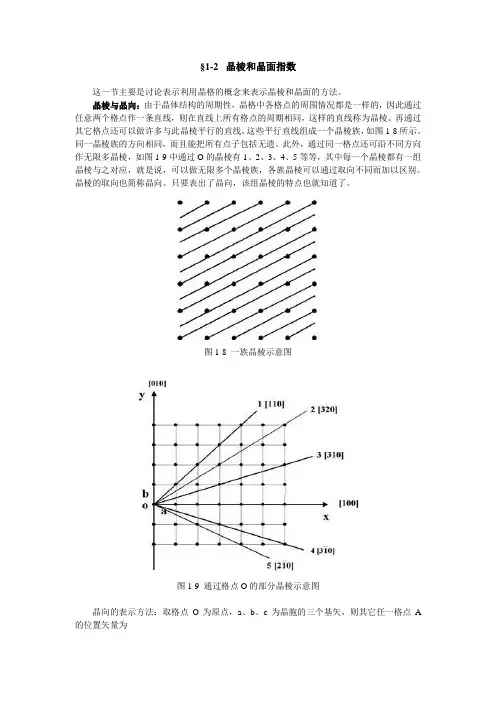
§1-2 晶棱和晶面指数这一节主要是讨论表示利用晶格的概念来表示晶棱和晶面的方法。
晶棱与晶向：由于晶体结构的周期性，晶格中各格点的周围情况都是一样的，因此通过任意两个格点作一条直线，则在直线上所有格点的周期相同，这样的直线称为晶棱。
再通过其它格点还可以做许多与此晶棱平行的直线，这些平行直线组成一个晶棱族，如图1-8所示。
同一晶棱族的方向相同，而且能把所有点子包括无遗。
此外，通过同一格点还可沿不同方向作无限多晶棱，如图1-9中通过O的晶棱有1、2、3、4、5等等，其中每一个晶棱都有一组晶棱与之对应，就是说，可以做无限多个晶棱族，各族晶棱可以通过取向不同而加以区别。
晶棱的取向也简称晶向。
只要表出了晶向，该组晶棱的特点也就知道了。
图1-8 一族晶棱示意图图1-9 通过格点O的部分晶棱示意图晶向的表示方法：取格点O为原点，a、b、c为晶胞的三个基矢，则其它任一格点A 的位置矢量为式中l1、l2、l3为整数（或有理数）。
取l1、l2、l3的互质比，即l1：l2：l3来表示晶棱OA 的方向，通常不直接用比例记号，该用方括号[l1l2l3]表示。
例如在图1-9中，晶棱1上A点为l1=1，l2=1，l3=0；B点为l1=2，l2=2，l3=0；比值为：l1:l2:l3=1:1:0=2:2:0，由此可得晶棱1的方向为[110]。
同理可得晶棱2的方向为[320]，晶棱4的方向为[30]，其中记号“”代表“-1”。
三个晶轴a、b、c的方向分别为[100]、[010]、[001]（c轴与图平面垂直，未画出）。
晶面与晶面指数：晶格中，还可以从各个方向上划分成无限多平面，即晶面族，如图1-10所示。
同一族晶面中，彼此距离相等，方向相同，格点在晶面上的分布也相同。
晶体的表面也是晶面，通常应该是原子面密度比较大的面。
现在问题是如何表示这些晶面族的方向。
图1-10 部分晶面族示意图从立体几何中知道，要描述一个平面的方向，就是表示出这个平面在三个坐标轴上的截距。
26.晶体学点群概念及种类？
晶体学点群的概念：
晶体的宏观对称操作的集合构成宏观对称操作群，即晶体学点群；晶体的宏观对称元素的集合构成宏观对称元素系（亦称对称型）。
宏观对称元素系并不是群，不过，二者具有一一对应的关系，所以，常用宏观对称元素系表示相应的晶体学点群。
晶体学点群有32种。
任何一种晶体必定属于32种晶体学点群之一。
32种晶体学点群代表互不相同的对称类型，但有些点群具有某种共同的对称元素，据此可以把32种晶体学点群归属于7种晶系。
方法是：规定出某些点群共有的、有代表性的对称元素作为一种晶系的特征对称元素，具备这种特征对称元素的几个点群就归属于这种晶系。
27.晶系的种类及名称？
举个例子：
28. 晶族的种类及名称？
6种晶族
六方晶系与三方晶系的正当晶胞的几何特征相同（a=b≠c，α=β= 90º，γ=120º），同属于六方晶族
详见27题中表
29. Bravais 格子的含义及种类？
7种晶系共有14种空间点阵型式，即14种Bravais格子。
平面点阵指标也称为晶面指标或米勒指数，是标志一族平面点阵在晶体中方向的一组3个互质整数(个别晶系有4个整数)，加圆括号记作(h*k*l*)。
晶面指标（h*k*l*）平面点阵指标需要经过三步才能写出：
（1）以a、b、c为度量单位，依次写出平面点阵在三条晶轴上的截数r、s、t；
（2）求倒易截数1/r、1/s、1/t；
（3）求出倒易截数的互质整数比h*：k*：l*，记作（h*k*l*），即为平面点阵指标。
（4）晶面与哪条坐标轴平行，相应的截数就是无穷大。
求倒易截数就是为了消除无穷大。
显然,相互平行的一族平面点阵，其（h*k*l* ）相同。
