1.1菱形的判定和性质小结

1.1菱形的性质及判定1．菱形的定义：有一组邻边相等的平行四边形叫做菱形． 2．菱形的性质菱形是特殊的平行四边形，它具有平行四边形的所有性质，•还具有自己独特的性质： ① 边的性质：对边平行且四边相等． ② 角的性质：邻角互补，对角相等．③ 对角线性质：对角线互相垂直平分且每条对角线平分一组对角． ④ 对称性：菱形是中心对称图形，也是轴对称图形．菱形的面积等于底乘以高，等于对角线乘积的一半．点评：其实只要四边形的对角线互相垂直，其面积就等于对角线乘积的一半． 3．菱形的判定判定①：一组邻边相等的平行四边形是菱形． 判定②：对角线互相垂直的平行四边形是菱形． 判定③：四边相等的四边形是菱形． 板块一、菱形的性质【例1】 ☆ ⑴菱形的两条对角线将菱形分成全等三角形的对数为⑵在平面上，一个菱形绕它的中心旋转，使它和原来的菱形重合，那么旋转的角度至少是【例2】 ⑴如图2，一活动菱形衣架中，菱形的边长均为16cm 若墙上钉子间的距离16cm AB BC ==，则1∠=度．⑵如图，在菱形ABCD 中，60A ∠=︒，E 、F 分别是AB 、AD 的中点，若2EF =，则菱形ABCD的边长是______．【例3】 如图，E 是菱形ABCD 的边AD 的中点，EF AC ⊥于H ，交CB 的延长线于F ，交AB 于P ，证明：AB 与EF 互相平分．【例4】 如图1所示，菱形ABCD 中，对角线AC 、BD 相交于点O ，H 为AD 边中点，菱形ABCD 的周长为24，则OH 的长等于．图21CBAP HFE DCBAE F D B C A【巩固】 如图，已知菱形ABCD 的对角线8cm 4cm AC BD DE BC ==⊥，，于点E ，则DE 的长为【例5】 菱形的周长为20cm ，两邻角度数之比为2:1，则菱形较短的对角线的长度为【巩固】 如图2，在菱形ABCD 中，6AC =，8BD =，则菱形的边长为（ ）A ．5B ．10C ．6D ．8【巩固】 如图3，在菱形ABCD 中，110A ∠=︒，E 、F 分别是边AB 和BC 的中点，EP CD ⊥于点P ，则FPC ∠=（ ）A ．35︒B ．45︒C ．50︒D ．55︒【例6】 ☆如图，把一个长方形的纸片对折两次，然后剪下一个角，为了得到一个锐角为60︒的菱形，剪口与折痕所成的角α的度数应为（ ）A ．15︒或30︒B ．30︒或45︒C ．45︒或60︒D ．30︒或60︒【巩固】 菱形ABCD 中，E 、F 分别是BC 、CD 的中点，且AE BC ⊥，AF CD ⊥，那么EAF ∠等于．【巩固】 如图，将一个长为10cm ，宽为8cm 的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（ ）A ．210cmB ．220cmC ．240cmD ．280cm图1HO DC BA图2DCBA图3E DP CF BA 图1DCBA【例7】 已知菱形ABCD 的两条对角线AC BD ，的乘积等于菱形的一条边长的平方，则菱形的一个钝角的大小是【例8】 如图，菱形花坛ABCD 的周长为20m ，60ABC ∠=︒，•沿着菱形的对角线修建了两条小路AC 和BD ，求两条小路的长和花坛的面积．【例9】 已知，菱形ABCD 中，E 、F 分别是BC 、CD 上的点，若AE AF EF AB ===，求C ∠的度数．板块二、菱形的判定 【例10】 如图，如果要使平行四边形ABCD 成为一个菱形，需要添加一个条件，那么你添加的条件是．【例11】 ☆如图，在ABC ∆中，BD 平分ABC ∠，BD 的中垂线交AB 于点E ，交BC 于点F ，求证：四边形BEDF 是菱形【巩固】 已知：如图，平行四边形ABCD 的对角线AC 的垂直平分线与边AD 、BC 分别相交于E 、F .求证：四边形AFCE 是菱形.【例12】 如图，在梯形纸片ABCD 中，//AD BC ，AD CD >，将纸片沿过点D 的直线折叠，使点C 落在AD 上的点C 处，折痕DE 交BC 于点E ，连结C E '.求证：四边形CDC E '是菱形．图2DFEDCBADCAB FEDCBAODEFCAB【例13】 ☆如图，E 是菱形ABCD 的边AD 的中点，EF AC ⊥于H ，交CB 的延长线于F ，交AB 于P ，证明：AB 与EF 互相平分【巩固】 ☆已知：如图，在平行四边形ABCD 中，AE 是BC 边上的高，将ABE ∆沿BC 方向平移，使点E与点C 重合，得GFC ∆．若60B ∠=︒，当AB 与BC 满足什么数量关系时，四边形ABFG 是菱形？证明你的结论．【例14】 如图，在ABC ∆中，AB AC =，M 是BC 的中点．分别作MD AB ⊥于D ，ME AC ⊥于E ，DF AC⊥于F ，EG AB ⊥于G ．DF EG 、相交于点P ．求证：四边形DM EP 是菱形．【例15】 如图，ABC ∆中，90ACB ∠=︒，AD 是BAC ∠的平分线，交BC 于D ，CH 是AB 边上的高，交AD于F ，DE AB ⊥于E ，求证：四边形CDEF 是菱形．【巩固】 ☆如图，M 是矩形ABCD 内的任意一点，将M AB ∆沿AD 方向平移，使AB 与DC 重合，点M 移动到点'M 的位置⑴画出平移后的三角形；⑵连结'MD MC MM ，，，试说明四边形'MDM C 的对角线互相垂直，且长度分别等于AB AD ，的长；⑶当M 在矩形内的什么位置时，在上述变换下，四边形'MDM C 是菱形？为什么？C'DC BA EAB CDEF P PF EDC B A GF E DCBAPMF E DG CBA HF DECBA三、与菱形相关的几何综合题 【例16】 已知等腰ABC △中，AB AC =，AD 平分BAC ∠交BC 于D 点，在线段AD 上任取一点P （A 点除外），过P 点作EF AB ∥，分别交AC 、BC 于E 、F 点，作PM AC ∥，交AB 于M 点，连结ME .⑴求证四边形AEPM 为菱形⑵当P 点在何处时，菱形AEPM 的面积为四边形EFBM 面积的一半？1. 菱形周长为52cm ，一条对角线长为10cm ，则其面积为．2.如图，在菱形ABCD 中，4AB a E =，在BC 上，2120BE a BAD P =∠=︒，，点在BD 上，则PE PC +的最小值为3. 已知菱形的一个内角为60︒，一条对角线的长为，则另一条对角线的长为________． 4.已知，菱形ABCD 中，E 、F 分别是BC 、CD 上的点，且60B EAF ∠=∠=︒，18BAE ∠=︒．求：CEF ∠的度数．5.如图，在ABC ∆中，AB AC =，D 是BC 的中点，连结AD ，在AD 的延长线上取一点E ，连结BE ，CE ．当AE 与AD 满足什么数量关系时，四边形ABEC 是菱形？并说明理由．6.如图，ACD ∆、ABE ∆、BCF ∆均为直线BC 同侧的等边三角形．已知AB AC =．⑴ 顺次连结A 、D 、F 、E 四点所构成的图形有哪几类？直接写出构成图形的类型和相应M'M DCBAMPFABCDE DBFEDCBAEDCB A的条件．⑵ 当BAC ∠为度时，四边形ADFE 为正方形．7.如图，已知BE 、CF 分别为ABC ∆中B ∠、C ∠的平分线，AM BE ⊥于M ，AN CF ⊥于N ，求证：MN BC ∥．FEDCBANMEFCBA。

1.1.1 菱形的性质与判定（第一课时）学习目标：掌握菱形的概念和性质在观察、操作、归纳等探索过程中，发展学生的合情推理能力，进一步培养学生数学说理的能力与习惯学习重点：菱形性质的探索过程学习难点：学生数学说理能力的培养学习过程：一、课前自主学习1、平行四边形的性质：。

2、平行四边形ABCD中，若∠A＝50 °，那么∠B＝∠C＝3、平行四边形ABCD中，AB+BC＝14 cm,则它的周长等于4、平行四边形ABCD中,对角线AC、BD交于点O,如果AC＝12，BD＝8,则AB的取值范围是.二、课内探索新知。

探索菱形的性质1、菱形的定义：2、菱形的性质：3、菱形的对称性：二、小组合作：1、已知菱形两条对角线长分别为12cm、8cm，则菱形的面积是,周长是2、已知菱形两邻角之比是5：1，若菱形的高是2cm，则菱形的周长是3、已知菱形ABCD中，若∠ABC＝120°，则BD：AC＝4、菱形两邻角之比为1：2，菱形周长为40cm,则较短对角线长为5、如图，四边形ABCD是菱形。

点O是两条对角线的交点，AB=5cm，AO=3cm，（1）求AC与BD的长。

（2）在（1）的情况下，则菱形的面积是多少三、展示反馈1、如图, 已知菱形ABCD的周长为20cm，∠A：∠ABC＝1：2，求∠ABD的度数与BD长。

2、已知菱形的两条对角线长分别为6和8，则它的边长为多少？3、菱形ABCD的周长为16厘米，∠ABC＝120°，求对角线BD与AC的长。

4、合作探究：如图，四边形ABCD是边长为13 cm的菱形，其中对角线BD长10 cm，求：(1)对角线AC的长度；(2)菱形ABCD的面积四、拓展延伸：1、已知菱形周长为80，一对角线长20，则相邻两角的度数为，。

2、如图，四边形ABCD是菱形。

对角线AC=6cm，DB=8cm，AH⊥BC于点H,求AH的长.3、将一个长为10cm，宽为8cm的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（）A．210cm B．220cm C．240cm D．280cm4．求证：菱形的对角线的交点到各边的距离相等。

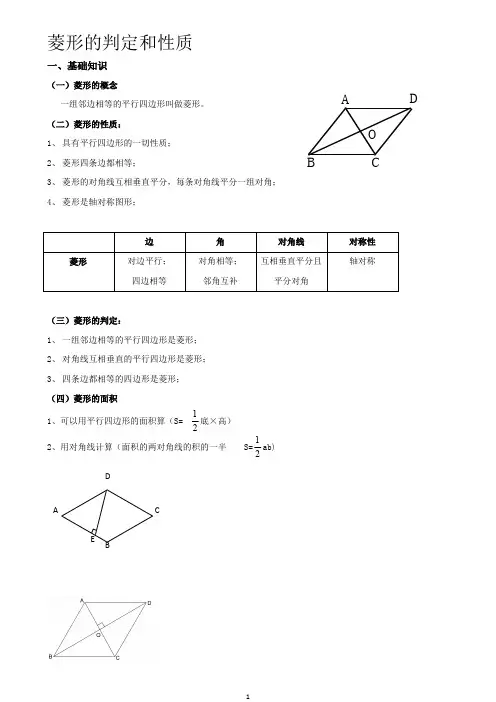
BCADO菱形的判定和性质一、基础知识（一）菱形的概念一组邻边相等的平行四边形叫做菱形。

（二）菱形的性质：1、 具有平行四边形的一切性质；2、 菱形四条边都相等；3、 菱形的对角线互相垂直平分，每条对角线平分一组对角；4、 菱形是轴对称图形；边 角 对角线 对称性 菱形对边平行； 四边相等对角相等； 邻角互补互相垂直平分且平分对角轴对称（三）菱形的判定：1、 一组邻边相等的平行四边形是菱形；2、 对角线互相垂直的平行四边形是菱形；3、 四条边都相等的四边形是菱形； （四）菱形的面积1、可以用平行四边形的面积算（S=21底×高） 2、用对角线计算（面积的两对角线的积的一半 S=21ab)ABCDE二、例题讲解考点一 ：菱形的判定例1：下列命题正确的是（ ）（A ） 一组对边相等，另一组对边平行的四边形一定是平行四边形 （B ） 对角线相等的四边形一定是矩形 （C ） 两条对角线互相垂直的四边形一定是菱形（D ） 两条对角线相等且互相垂直平分的四边形一定是正方形 练习1：菱形的对角线具有( ) A ．互相平分且不垂直 B ．互相平分且相等 C ．互相平分且垂直 D ．互相平分、垂直且相等练习2：如图，菱形ABCD 中，对角线AC 、BD 相交于点O ，M 、N 分别是边AB 、AD 的中点，连接OM 、ON 、MN ，则下列叙述正确的是（ ） A ．△AOM 和△AON 都是等边三角形B ．四边形AMON 与四边形ABCD 是位似图形C ．四边形MBON 和四边形MODN 都是菱形D ．四边形MBCO 和四边形NDCO 都是等腰梯形练习3：如图，在三角形ABC 中，AB ＞AC ，D 、E 分别是AB 、AC 上的点，△ADE 沿线段DE 翻折，使点A 落在边BC 上，记为A '．若四边形ADA E '是菱形，则下列说法正确的是( )A ．DE 是△ABC 的中位线B ．AA '是BC 边上的中线 C ．AA '是BC 边上的高D ．AA '是△ABC 的角平分线ABCDEA 'DBCA NM O练习4：如图，下列条件之一能使平行四边形ABCD 是菱形的为（ ） ①AC BD ⊥ ②90BAD ∠= ③AB BC = ④AC BD = A ．①③B ．②③C ．③④D ．①②③例2 ：已知AD 是△ABC 的平分线，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ，则四边形AEDF 是什么四边形？请说明理由．变化：若D 是等腰三角形底边BC 的中点，DE ∥AC 交AB 于E ，DF ∥AB 交AC 于F ，则四边形AEDF 是什么四边形？请说明理由．练习1：如图，AD 是Rt △ABC 斜边上的高，BE 平分∠B 交AD 于G ，交AC 于E ，过E 作EF ⊥BC 于F ，试说明四边形AEFG 是菱形．练习2：如图，E 是菱形ABCD 边AD 的中点，EF ⊥AC 于点H ，交CB 延长线于点F ，交AB 于点G ，求证：AB 与EF 互相平分。

《菱形》知识清单一、菱形的定义在同一平面内，有一组邻边相等的平行四边形是菱形。

需要注意的是，菱形首先是平行四边形，然后还需要满足邻边相等这一条件。

二、菱形的性质1、边的性质菱形的四条边都相等。

这是菱形区别于一般平行四边形的重要特征之一。

因为平行四边形对边相等，而菱形在此基础上，邻边也相等，所以四条边长度均相等。

2、角的性质菱形的对角相等，邻角互补。

这与平行四边形的角的性质是一致的。

3、对角线的性质菱形的对角线互相垂直且平分，并且每条对角线平分一组对角。

对角线互相垂直这一性质使得菱形具有很多独特的特点和应用。

比如，在计算菱形的面积时，就可以利用对角线的长度来计算。

4、对称性菱形是中心对称图形，对称中心是两条对角线的交点。

同时，菱形也是轴对称图形，两条对角线所在的直线就是它的对称轴。

5、面积计算菱形的面积可以用两种方法计算：（1）底乘以高，这与计算平行四边形面积的方法相同。

（2）对角线乘积的一半。

即 S ＝ 1/2 ×对角线 1 ×对角线 2 。

三、菱形的判定1、一组邻边相等的平行四边形是菱形。

这是根据菱形的定义得出的判定方法。

2、对角线互相垂直的平行四边形是菱形。

如果一个平行四边形的对角线互相垂直，那么它一定是菱形。

3、四条边都相等的四边形是菱形。

这一判定方法直接从边的长度来判断。

四、菱形性质与判定的应用1、在几何证明中的应用在证明几何问题时，如果已知图形是菱形，可以利用菱形的性质来得出相关的结论。

例如，如果知道一个四边形是菱形，就可以得出它的对角线互相垂直等结论。

2、在实际生活中的应用菱形在实际生活中有很多应用。

比如，菱形的图案经常出现在建筑装饰、纺织品设计等方面，因为其美观且具有一定的稳定性。

3、在数学计算中的应用在计算菱形的周长、面积等问题时，需要熟练运用菱形的性质和相关公式。

五、与其他图形的关系1、菱形与平行四边形菱形是特殊的平行四边形，具有平行四边形的一切性质。

2、菱形与矩形矩形的四个角都是直角，而菱形的角不一定是直角。

菱形知识点总结1. 菱形与其特性菱形是几何学中的一个基本形状，具有许多独特的特性。

菱形是一个四边形，其四边相等且对角线相等。

以下是一些关于菱形的重要特性：•四个边相等：菱形的四条边长度相等，这意味着它具有对称性。

•对角线相等：菱形的两条对角线相等，即对角线的长度相等。

•对角线互相垂直：菱形的两条对角线互相垂直，即形成90度的角。

•对角线平分角：菱形的两条对角线可以平分角，也就是说，每条对角线划分出的角度相等。

2. 菱形的公式菱形是一个多边形，有一些与其相关的重要公式和性质。

以下是几个与菱形相关的公式：•菱形的面积公式：菱形的面积可以使用以下公式计算：面积 = 对角线1长度 × 对角线2长度 × 0.5•菱形的周长公式：菱形的周长可以使用以下公式计算：周长 = 4 × 边长•菱形的对角线长度公式：已知菱形的边长时，可以使用以下公式计算对角线的长度：对角线长度 = 边长× √23. 菱形的应用场景菱形在日常生活和工程领域中有各种应用。

以下是几个常见的应用场景：•计算建筑物屋顶的面积：当屋顶形状是一个平面菱形时，可以使用菱形的面积公式来计算屋顶的面积。

这对建筑师和工程师来说是一个非常有用的计算方法。

•制作钻石和宝石：菱形被广泛用于制作钻石和宝石的形状。

这是因为菱形有一种独特而美丽的外观，非常适合制作珠宝。

•几何学教育：菱形是几何学中的基本形状之一，它常常被用于教育和学习几何学。

通过学习菱形的特性和公式，学生可以更好地理解和应用几何学的概念。

4. 菱形的实例以下是一些常见的菱形实例：*************************这个图案是一个典型的菱形，由星号组成。

可以通过在编程语言中使用循环来创建这样的图案。

5. 总结菱形是一个常见的几何形状，具有许多独特的特性和应用。

了解菱形的特性和相关公式对于解决几何学问题和应用菱形的实际场景非常重要。

通过学习菱形，我们可以更好地理解和应用几何学的概念，同时也能欣赏到菱形的美丽和独特之处。