自然数的整除

数的整除性质、特征【知识要点】：整除性质：（1）如果数a、b都能被c整除，那么它们的和（a+b）或差（a－b）也能被c整除。

（2）如果数a能被自然数b整除，自然数b能被自然数c整除，则数a必能被数c整除。

（3）若干个数相乘，如其中有一个因数能被某一个数整除，那么，它们的积也能被这个数整除。

（4）如果一个数能被两个互质数中的每一个数整除，那么，这个数能被这两个互质数的积整除。

反之，若一个数能被两个互质数的积整除，那么这个数能分别被这两个互质数整除。

整除特征：1、能被2整除的数：个位数能被2整除，则这个数就能被2整除。

如个位上是2、4、6、8、0的数都能被2整除。

2、每一位上数字之和能被3整除，那么这个数就能被3整除。

3、最后两位能被4整除的数，这个数就能被4整除。

4、个位上是0或5的数都能被5整除。

5、一个数只要能同时被2和3整除，那么这个数就能被6整除。

6、把个位数字截去，再从余下的数中，减去个位数的2倍，如果差是7的倍数，则原数能被7整除。

另外，把末三位数字截去，再从余下的数中减去截去的末三位数，如果差是7的倍数，则原数能被7整除。

7、最后三位能被8整除的数，这个数就能被8整除。

8、每一位上数字之和能被9整除，那么这个数就能被9整除。

9、若一个整数的末位是0，则这个数能被10整除。

10、若一个整数的奇位数字之和与偶位数字之和的差值能被11整除，则这个数能被11整除。

另外1，把个位数字截去，再从余下的数中，减去个位数，如果差是11的倍数，则原数能被11整除。

另外2，把末三位数字截去，再从余下的数中减去截去的末三位数，如果差是11的倍数，则原数能被11整除.12、若一个整数能被3和4整除，则这个数能被12整除。

13、若一个整数的个位数字截去，再从余下的数中，加上个位数的4倍，如果差是13的倍数，则原数能被13整除。

另外，把末三位数字截去，再从余下的数中减去截去的末三位数，如果差是13的倍数，则原数能被13整除.14、若一个整数能被2和7整除，则这个数能被14整除。

小升初总复习数与代数第一单元数的认识第2节数的整除知识梳理典例精讲【例1】把自然数A和B分解质因数后分别是A=2×3×11×m，B=2×3×7×m。

A、B两数的最大公因数是78，这两个数的最小公倍数是多少？【分析】这里要明白最大公因数和最小公倍数的意义，A、B两数的最大公因数就是这两个数的全部公有的质因数的积，也就是2×3×m；A、B两数的最小公倍数就是这两个数的全部公有质因数及各自独有质因数的积，也就是2×3×m×11×7.根据两个数的最大公因数是78，求出m的值，本题便迎刃而解。

【解】因为2×3×m=78，所以m=78÷2×3=13，因此2×3×m×11×7=78×11×7=155。

答：这两个数的最小公倍数是155.即时演练1.25和30的最大公因数是（），最小公倍数是（）。

2. 把自然数A和B分解质因数后分别是A=2×3×m，B=2×7×m。

A、B两数的最大公因数是22，这两个数的最小公倍数是多少？3.两个数的最小公倍数是150，最大公因数是15.这两个数分别是（）和（）。

【例2】有一些糖果，如果把6个装一包少1个；如果8个装一包也少一个；如果把5个装一包还是少一个。

这些糖果至少有多少个？【分析】这些糖果，把6个装一包少1个说明糖果的总个数比6的倍数少1个；8个装一包也少一个说明糖果总个数比8的倍数少1个；把5个装一包还是少一个说明糖果的总个数比5的倍数少1个。

所以这些糖果的总个数比5、6、8的公倍数少1，这里求至少有糖果多少个，就是求比5、6、8的最小公倍数少1的数。

【解】5、6、8的最小公倍数是120.120-1=119（个）答：这些糖果至少有119个。

数的整除性质1：如果数a、b都能被c整除，那么它们的和（a+b）或差(a－b)也能被c整除。

性质2：几个数相乘，如果其中有一个因数能被某一个数整除，那么它们的积也能被这个数整除。

能被2整除的数，个位上的数能被2整除（偶数都能被2整除），那么这个数能被2整除能被3整除的数，各个数位上的数字和能被3整除，那么这个数能被3整除能被5整除的数，个位上的数都能被5整除（即个位为0或5）那么这个数能被5整除能被7整除的数，若一个整数的个位数字截去，再从余下的数中，减去个位数的2倍，如果差是7的倍数，则原数能被7整除。

能被11整除的数，奇数位（从左往右数）上的数字和与偶数位上的数字和之差（大数减小数）能被11整除，则该数就能被11整除。

例1在下面的数中，哪些能被4整除？哪些能被8整除？哪些能被9整除？234，789，7756，8865，3728，8064。

例2从0，2，5，7四个数字中任选三个，组成能同时被2，5，3整除的数，并将这些数从小到大进行排列。

例3六位数是6的倍数，这样的六位数有多少个？例4要使六位数能被36整除，而且所得的商最小，问A，B，C各代表什么数字？1、能被3整除的最小三位数是（），能被5整除的最大三位数是（）2，又能被3整除，而且还是5的倍数的最小三位数是（）3、在自然数中，（）既不是质也不是合。

既是奇数又是质数的最小的数是（），（）既是质数又是合数。

4、用三个一位质数组成能同时被3和5整除的三位数，最大的是（），最小的数是（）。

4、自然数a除以自然数b，商是15，那么a和b的最大公约数是（）。

5、三个质数的最小公倍数是42，这三个质数是（）。

6、100以内同时能被3和7整除的最大奇数是（），最大偶数是（）。

1．6539724能被4，8，9，24，36，72中的哪几个数整除？2．个位数是5，且能被9整除的三位数共有多少个？3．一些四位数，百位上的数字都是3，十位上的数字都是6，并且它们既能被2整除又能被3整除。

数的整除性质主要有：（1）若甲数能被乙数整除,乙数能被丙数整除，那么甲数能被丙数整除。

（2）若两个数能被一个自然数整除,那么这两个数的和与差都能被这个自然数整除。

（3）几个数相乘，若其中有一个因数能被某一个数整除，那么它们的积也能被这个数整除.（4）若一个数能被两个互质数中的每一个数整除，那么这个数也能被这两个互质数的积整除。

（5）若一个数能被两个互质数的积整除，那么这个数也能分别被这两个互质数整除。

（6）若一个质数能整除两个自然数的乘积，那么这个质数至少能整除这两个自然数中的一个。

（7）个位上是0、2、4、6、8的数都能被2整除.（8）个位上是0或者5的数都能被5整除.（9）若一个整数各位数字之和能被3（或9)整除，则这个整数能被3（或9）整除。

（10）若一个整数末尾两位数能被4整除，则这个数能被4整除.（11）若一个整数末尾三位数能被8整除，则这个数能被8整除。

（12）若一个整数各位数字之和能被9整除,则这个整数能被9整除.（13）一个三位以上的整数能否被7（11或13)整除，只须看这个数的末三位数字表示的三位数与末三位数字以前的数字所组成的数的差（以大减小)能否被7（11或13）整除（14）末位数字为零的整数必能被10整除（15）另外,一个整数的奇数位数字和与偶数位数字和的差如果是11的倍数，那么这个整数也是11的倍数。

（一个整数的个位、百位、万位、…称为奇数位，十位、千位、百万位……称为偶数位.）（16）至于6和12的整除特性，通过以上的原则判断即可:各位数之和能被3整除的偶数能被6整除;各位数之和能被3整除且末两位数字组成的两位数能被4整除的整数能被12整除。

（17）能被7整除的数的特征：若一个整数的个位数字去掉，再从余下的数中,减去个位数的2倍，如果差是7的倍数,则原数能被7整除.如果数字仍然太大不能直接观察出来，就重复此过程。

方法1、（适用于数字位数少时）一个数割去末位数字，再从留下来的数中减去所割去数字的2倍，这样，一次次减下去，如果最后的结果是7的倍数（包括0）,那么，原来的这个数就一定能被7整除．例如:判断133是否7的倍数的过程如下：13－3×2＝7，所以133是7的倍数；又例如判断6139是否7的倍数的过程如下：613－9×2＝595 ，59－5×2＝49，所以6139是7的倍数,余类推.方法2、（适用于数字位数在三位以上）一个多位数的末三位数与末三位以前的数字所组成的数之差，如果能被7整除，那么，这个多位数就一定能被7整除．如判断数280679末三位数字是679,末三位以前数字所组成的数是280，679－280=399，399能被7整除,因此280679也能被7整除。

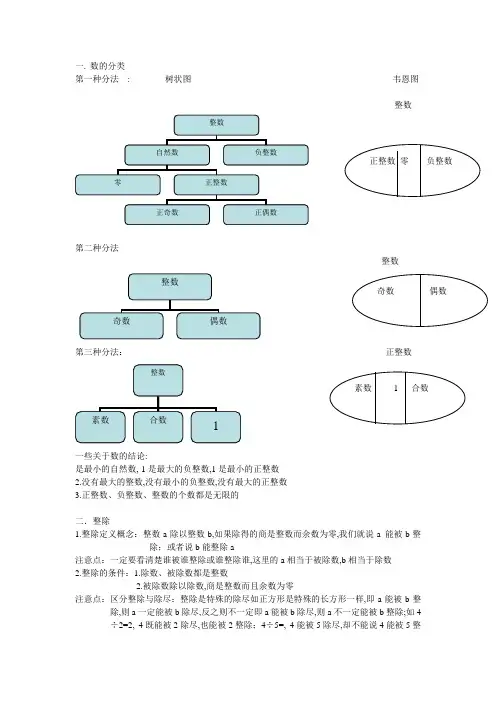
一. 数的分类第一种分法 : 树状图 韦恩图整数第二种分法 整数第三种分法： 正整数一些关于数的结论:是最小的自然数,-1是最大的负整数,1是最小的正整数2.没有最大的整数,没有最小的负整数,没有最大的正整数3.正整数、负整数、整数的个数都是无限的二．整除1.整除定义概念：整数a 除以整数b,如果除得的商是整数而余数为零,我们就说a 能被b 整除；或者说b 能整除a注意点：一定要看清楚谁被谁整除或谁整除谁,这里的a相当于被除数,b 相当于除数2.整除的条件：1.除数、被除数都是整数2.被除数除以除数,商是整数而且余数为零注意点：区分整除与除尽：整除是特殊的除尽如正方形是特殊的长方形一样,即a 能被b 整除,则a 一定能被b 除尽,反之则不一定即a 能被b 除尽,则a 不一定能被b 整除;如4÷2=2, 4既能被2除尽,也能被2整除；4÷5=, 4能被5除尽,却不能说4能被5整除三．因数与倍数1.因数与倍数的定义：整数a能被整数b整除,a 就叫做b的倍数,b就叫做a的因数约数;注意点：1.因数和倍数是相互依存的,不能简单的说某个数是因数,某个数是倍数;如：6÷3=2,不能说6是倍数,3是因数；要说6是3的倍数,3是6的因数;2.因数与倍数是建立在整除的基础上的,所以如4÷=20,一般是不说4是的倍数,是4的因数;2.因数与倍数的特点：一个整数的因数中最小的因数是1,最大的因数是它本身;一个数的倍数中最小的倍数是这个数本身,没有最大的倍数;因数的个数是有限的,都能一一列举出来,倍数的个数是无限的;3.求一个数因数的方法：利用积与因数的关系一对一对找,找出哪两个数的乘积等于这个数,那么这两个数就是这个数的因数;如16=1×16=2×8=4×4,那么16的因数就有1、2、4、8、16,计算时一定不要忘了1和这个数本身都是它的因数,注意按照一定的顺序以防遗漏;4.求一个数倍数的方法：这个数本身分别乘以1、2、3、4、5……即正整数得到的积就是这个数的倍数;若用n表示所有的正整数,则2的倍数可表示为2n, 5的倍数可表示为5n四．能被2、5、3整除的数的特点1.能被2整除的数即2的倍数个位上的数字是0、2、4、6、8,反之,个位上的数字是0、2、4、6、8的数也能被2整除2.能被5整除的数即5的倍数个位上的数字是0、5,反之,个位上的数字是0、5的数都能被5整除3.能被3整除的数即3的倍数各个位数上的数字之和是3的倍数,反之,各个位数上的数字之和是3的倍数的数都能被3整除4.能被2、5同时整除的数的个位数字都是0,个位数字为0的数也能被10整除,能被10整除的数一定能被2或5其中的一个或两个同时整除;五．奇数、偶数1.奇数与偶数的定义：能被2整除的整数叫做偶数,不能被2整除的整数叫做奇数;按照能否被2整除来划分奇数与偶数2.奇数个位数上的数的特点：1、3、5、7、9偶数个位数上的数的特点：0、2、4、6、83.在连续的正整数中除1外,与奇数相邻的两个数是偶数,与偶数相邻的两个数是奇数4.相邻的奇数或偶数数字相差2,奇数可用2n-1或2n+1表示,偶数可用2n表示;5.奇数与偶数加法和乘法的运算特点奇数+奇数=偶数偶数+偶数=偶数奇数+偶数=奇数奇数×奇数=奇数偶数×偶数=偶数奇数×偶数=偶数利用此结论可检验一些运算是否正确,同时也要注意结论的逆向运用,如偶数奇数可拆成哪些奇数或偶数的和、积六.素数、合数1.素数与合数定义：一个正整数如果只有1和它本身两个因数,这样的数叫做素数质数,如果除了1和它本身以外还有别的因数,这样的数叫做合数;注意点：1.素数与合数的分类方法是根据它们因数的个数来分的,素数只有2个因数1和本身,合数至少有三个因数；任何一个数除1外都有1和它本身两个因数;2. 1既不是素数也不是合数;3．最小的素数是2,最小的合数是42.素数与奇数的联系和区别奇数不一定都是素数;√1既不是素数也不是合数,9、15等是奇数但是合数所有素数都是奇数; ×2是素数,但2是偶数3.合数与偶数的联系与区别合数不一定都是偶数;√9、15等都是合数,但它们是奇数偶数都是合数; ×2是偶数但2是素数注意:判断题对的要说明原因,错的要举出反例;七．素因数与分解素因数1.素因数与分解素因数的定义：每个合数都可以写成几个素数相乘的形式,其中每个素数都是这个合数的因数,叫做这个合数的素因数;把一个合数用素因数相乘的形式表示出来,叫做分解素因数;注意：1.求一个数的素因数时,先把这个数分解素因数,有几个素因数就写几个;如24=2×2×2×3,则素因数是2、2、2、3,而不是2、32.因数与素因数的区别：因数可以是素数或合数,素因数一定是素数;一个数的素因数一定是这个数的因数,因数的个数一定比素因数的个数多;2.分解素因数的方法树枝分解法：过程中注意不要漏写乘号,分解要彻底,直到没有合数出现,也不能出现1.要分解的合数写在等号左边,把它的素因数用相乘的形式写在等号右边,再把这几个素因数按从小到大的顺序排列;短除法：1.先用一个能整除这个合数的素数去除通常从最小的开始,偶数肯定先用2除,奇数一般从3开始一个个带入验算2.得出的商如果是合数,再按照上面的方法继续除下去,直到得出的商是素数为止;3.然后把各个除数和最后的商按从小到大的顺序写成连乘的形式;3.由一个数分解素因数求这个数的因数12=2×2×3,素因数是2、2、3,除1外由单个的素因数组成因数有2、3,由两个素因数组成的因数有2×2=4,2×3=6,由三个素因数组成的因数有2×2×3=12,所以12的因数有1、2、3、4、6、12.4. 由一个数分解素因数求这个数因数的个数1所有素因数都相同时,因数的个数是它素因数的个数+1,如8=2×2×2,素因数是2、2、2,则8的因数的个数是它素因数的个数+1,即4个2素因数不完全相同时,因数的个数是每个素因数个数+1后相乘的积,如12=2×2×3,素因数2的个数是2,素因数3的个数是1,则12的因数的个数是2+1×1+1=6八.公因数与最大公因数1.公因数与最大公因数定义:几个数公有的因数,叫做这几个数的公因数,其中最大的一个叫做这几个数的最大公因数.2.互素定义：如果两个整数只有公因数1,那么称这两个数互素;如8和9注意：互素是两个数之间,素数是指一个数,互素的两个数的最大公因数就是1.两个互素的数未必都是素数; √8和9互素,但8和9都是合数两个不同的素数一定互素. √若缺少“不同的”,则错,因为3和3都是素数但不互素3. 求两个数最大公因数的方法：1 一般方法：写出两个数所有的因数,再找出它们共同的最大的因数2 分解素因数的方法：把这两个数分解素因数,再找出相同的素因数,把它们所有的公有的素因数相乘,所得的积就是它们的最大公因数;3 短除法：先用这两个数公有的素因数去除一般从最小的素因数开始,得出的商如果是合数,再按照上面的方法继续除下去,直到两个数互素为止,这两个数的最大公因数就是左侧的除数的乘积. 类比用短除法分解素因数的方法4. 两个整数中,如果某个数是另一个数的因数,那么这个数就是这两个数的最大公因数;如果这两个数互素,那么它们的最大公因数就是1.九.公倍数和最小公倍数1.公倍数与最小公倍数定义:几个整数公有的倍数叫做它们的公倍数,其中最小的一个叫做它们的最小公倍数.2.求两个数最小公倍数的方法:1一般方法:从小到大分别依次写出几个这两个数的倍数,再找出它们共同的最小的倍数2分解素因数的方法: 把这两个数分解素因数,再找出相同的素因数,再取各自剩余的素因数,将这些数连乘所得的积,就是这两个数的最小公倍数.3短除法: 先用这两个数公有的素因数去除一般从最小的素因数开始,得出的商如果是合数,再按照上面的方法继续除下去,直到两个数互素为止,这两个数的最小公倍数就是左侧的除数与底部商的乘积.注意点:1.用短除法求两个数的最大公因数和最小公倍数时,过程都相同,只是最后写结论时注意需要乘哪些数.2.求两个数的最大公因数和最小公倍数,先判断这两个数是否存在因数倍数关系或互素关系,存在因数倍数关系时,最大公因数就是较小的那个数,最小公倍数就是较大的那个数;两数互素时,最大公因数就是1,最小公倍数就是它们的乘积.3.两个整数的公倍数一定能被这两个数整除.十.求三个整数的最大公因数和最小公倍数拓展1求三个整数的最大公因数:同样也是三种方法,只需找出三个数共同的因数,最大的因数就是最大公因数.注意与三个数的最小公倍数区分2求三个整数的最小公倍数:一般方法:写出三个数的倍数,再找出最小公倍数.分解素因数法:分别分解素因数,先找出三个数共同的素因数,再找出每两个数公有的素因数,再取各自剩余的素因数,把这些素因数连乘所得的积就是这三个数的最小公倍数.短除法:先用三个数公有的素因数去除直到三个数没有公有的素因数,再用其中两个数公有的素因数去除,直到除得的三个商两两互素为止即三对互素数。

第一章数的整除第一节整数和整除‎教学目标：1、理解整除的‎定义和自然‎数的意义。

知道整除的‎要素，掌握整除的‎两种表述方‎法。

2、理解因数与‎倍数的意义‎，会求一个整‎数的因数和‎倍数。

3、概括出能被‎2，5整除的数‎的特征。

知识要点：1.1：整数和整除‎的意义1、零和正整数‎统称为自然‎数。

2、正整数、零、负整数，统称为整数‎。

3、整数a除以‎整数b，如果除得的‎商是整数而‎余数为零，我们就说a‎能被b整除‎；或者说b能‎整除a.注意整除的‎条件：1、除数、被除数都是‎整数；2、被除数除以‎除数，商是整数而‎且余数为零‎。

1.2：因数和倍数‎1、整数a能被‎整数b整除‎，a就叫做b‎的倍数，b就叫做a‎的因数（也称约数）。

2、一个整数的‎因数中最小‎的因数是1‎，最大的因数‎是它本身。

1.3：能被2、5整除的数‎1、个位上是0‎，2，4，6，8的整数都‎能被2整除‎。

2、能被2整除‎的整数叫做‎偶数，不能被2整‎除的整数叫‎做奇数。

3、各位上是0‎或者5的整‎数都能被5‎整除。

第二节分解素因数‎教学目标：1、理解素数、合数的意义‎。

2、能用求因素‎的方法或查‎素数表的方‎法判断一个‎正整数是否‎为素数。

3、熟记20以‎内的全部素‎数。

4、理解素因数‎和分解素因‎数的意义，掌握分解素‎因数的方法‎。

5、掌握最大公‎因数和最小‎公倍数的算‎理和方法。

知识要点：1.4：素数、合数与分解‎素因数1、一个正整数‎，如果只有1‎和它本身两‎个因素，这样的数叫‎做素数，也叫做质数‎；如果除了1‎和它的本身‎以外还有别‎的因素，这样的数叫‎做合数。

2、1既不是素‎数，也不是合数‎。

这样，正整数又可‎以分为1、素数和合数‎三类。

34、每个合数都‎可以写成几‎个素数相乘‎的形式，其中每个素‎数都是这个‎合数的因数‎，叫做这个合‎数的素因数‎。

把一个合数‎用素因素相‎乘的形式表‎示出来，叫做分解素‎因数。

5、一般我们用‎短除法分解‎素因数，步骤如下：①先用一个能‎整除这个合‎数的素数（通常从最小‎的开始）去除。

第二讲数的整除特性讲义（一）整除的定义：所谓“一个自然数a能被另一个自然数b整数”就是说“商a/b是一个整数”；或者换句话说：存在这第三个自然数c，使得a=b×c，这时候我们就说“b整除a”或者“a能被b整除”，其中b叫a的约数，a是b的倍数，记做“b︱a”（二）整除的性质：（传递性）若c︱b，b︱a，则c︱a（可加性）若c︱a，c︱b，则c︱（a+b）（可乘性）若c︱a，d︱b，则cd︱ab（三）常见的整除特征：尾数系：一个数的末位能被2或5整除，这个数就能被2或5整除；一个数的末两位能被4或25整除，这个数就能被4或25整除；一个数的末三位能被8或125整除，这个数就能被8或125整除；数字和系：一个位数数字和能被3整除，这个数就能被3整除；一个数各位数数字和能被9整除，这个数就能被9整除；分段做差系：如果一个整数的奇数位上的数字之和与偶数位上的数字之和的差能被11整除，那么这个数能被11整除.如果一个整数的末三位与末三位以前的数字组成的数之差能被7、11或13整除，那么这个数能被7、11或13整除.课后习题基础篇：【闯关1】493至少增加（）才是3的倍数，至少减少（）才有因数5，至少增加（）才是2的倍数，至少增加（）才是7的倍数。

【闯关2】如果六位数1992□□能被105整除，那么它的最后两位数是多少？提高篇：【闯关3】如果四位数x=6□□8能被236整除，那x除以236所得的商为________。

【闯关4】从50到100的这51个自然数的乘积的末尾有多少个连续的0？巅峰篇：【闯关5】试说明一个4位数，原序数与反序数的和一定是11的倍数(如：1236为原序数，那么它对应的反序数为6321，它们的和7557是11的倍数．)第二讲数的整除特性课后习题：基础篇：【闯关1】493至少增加（）才是3的倍数，至少减少（）才有因数5，至少增加（）才是2的倍数，至少增加（）才是7的倍数。

解析：一个位数数字和能被3整除，这个数就能被3整除；4+9+3=16，所以至少增加2就是3的倍数。

能被4、6、9整除数的特征我们在三年级已经学习了能被2，3，5整除的数的特征，这一讲我们将讨论整除的性质，并讲解能被4，8，9整除的数的特征。

数的整除具有如下性质：性质1 如果甲数能被乙数整除，乙数能被丙数整除，那么甲数一定能被丙数整除。

例如，48能被16整除，16能被8整除，那么48一定能被8整除。

性质2 如果两个数都能被一个自然数整除，那么这两个数的和与差也一定能被这个自然数整除。

例如，21与15都能被3整除，那么21＋15及21-15都能被3整除。

性质3 如果一个数能分别被两个互质的自然数整除，那么这个数一定能被这两个互质的自然数的乘积整除。

例如，126能被9整除，又能被7整除，且9与7互质，那么126能被9×7＝63整除。

利用上面关于整除的性质，我们可以解决许多与整除有关的问题。

为了进一步学习数的整除性，我们把学过的和将要学习的一些整除的数字特征列出来：（1）一个数的个位数字如果是0，2，4，6，8中的一个，那么这个数就能被2整除。

（2）一个数的个位数字如果是0或5，那么这个数就能被5整除。

（3）一个数各个数位上的数字之和如果能被3整除，那么这个数就能被3整除。

（4）一个数的末两位数如果能被4（或25）整除，那么这个数就能被4（或25）整除。

（5）一个数的末三位数如果能被8（或125）整除，那么这个数就能被8（或125）整除。

（6）一个数各个数位上的数字之和如果能被9整除，那么这个数就能被9整除。

其中（1）（2）（3）是三年级学过的内容，（4）（5）（6）是本讲要学习的内容。

因为100能被4（或25）整除，所以由整除的性质1知，整百的数都能被4（或25）整除。

因为任何自然数都能分成一个整百的数与这个数的后两位数之和，所以由整除的性质2知，只要这个数的后两位数能被4（或25）整除，这个数就能被4（或25）整除。

这就证明了（4）。

类似地可以证明（5）。

（6）的正确性，我们用一个具体的数来说明一般性的证明方法。

数的整除特征★知识要点1、如果一个数的个位数字能被2或5整除，则这个数能被2或5整除。

2、如果一个数的末两位数字能被4或25整除，则这个数就能被4或25整除。

3、如果一个数的末三位数字能被8或125整除，则这个数就能被8或125整除。

4、如果一个数的各位数字之和能被3或9整除，则这个数就能被3或9整除。

5、如果一个自然数的奇数位上数字和与偶数位上数字和的差（大数减小数）能被11整除，那么这个数就能被11整除。

6、被7、11、13整除数的特征：如果一个自然数的末三位数字所表示的数与末三位前的数字所表示的数之差（大数减小数）能被7、11或13整除，那么这个数就能被7，11或13整除。

★典型例题例1、在□内填上适当的数，使五位数5874□能被2整除，这样的五位数有多少个？例2、在□内填上适当的数，使六位数69547□能被4或25整除。

例3、在□内填上适当的数，使五位数31□26能被3或9整除。

例4、在865后面补上3个数字，组成一个六位数，使它能被3，4，5整除，且使这个数值尽可能地大。

例5、在五位数15□8□的□内填什么数字，才能使它既能被3整除，又含有因数5？例6、根据被11整除的数的特征，判别下列数中哪几个能被11整除：3434 3443 52019 68868例7、判断2146455311能否被7，11或13整除？课堂练习1、在□内填上适当的数，使四位数139□能被5整除，这样的四位数有哪几个？2、在□内填上适当的数，使七位数7132□20能被8整除。

3、判断下列哪些数能被25整除，哪些能被125整除？能被125整除的数一定能被25整除吗？反之能被25整除的数一定能被125整除吗？750 765 2775 6325 1500 10004、根据被3和9整除的数的特征，用“去三法”或“或九法”判别下列数中哪些数能被3整除，哪些能被9整除。

请仔细观察能被9整除的数一定能被3整除吗？反之能被3整除的数一定能被9整除吗？请牢记这个规律！5646 49257 25341 87203 56142365、在358后面补上3个数字，组成一个六位数，使它能分别被3、4、5整除，且使这个数值尽可能地小。