预初作业-数的整除综合

预初数学阶段测试复习一班级___________姓名___________学号__________一、填空题：1. 正整数按因数的个数可分为____________，____________和____________.2. _____________，_____________和_____________统称为整数.3. 在1到20的整数中，_ __ ___是素数，____ __是合数，____ 既是素数又是偶数，____ 既是合数又是奇数，______既不是素数也不是合数.4. ①12÷5、②91÷7、③3.2÷0.4、④15÷7、⑤3÷12、⑥78÷6在以上的除法算式里，其中属于整除的式子有______________,属于除尽的式子有________________________.5. 若8=÷n m （n m ,是正整数），则__________能整除__________；__________是__________的倍数；n m ,的最大公因数是_______,最小公倍数是_______.6. 能被24整除的数的因数至少有______________________________7. 18的所有因数中，互素的数有____________对.8. 在4，5，7，0，这四个数中不重复地挑三个数组成的三位数中能同时被2，3整除的最小三位数是__________,最大三位数是__________.9. 用10以内的素数组成一个被3整除的最大三位数是 .10. 一个三位数15□，能被3和2整除，□内可以填________________.11. 一个数的最小倍数和它的最小因数之和为43，则这个数的因数有______________.12. 将182分解素因数___________________________________.13. 60和48的公因数有_______________,公有的素因数有__________________.14. 已知A=753⨯⨯，则A 的因数是合数的有_____________________________.15. 42和66分别除以一个正整数a 所得的余数都是6，则这个正整数a 为________.16. 已知A=a 732⨯⨯⨯,B=b 52⨯⨯,A 、B 的最大公因数是70，则a=_______，b=________.17. 数a 与数b 是互素数，它们的最小公倍数是最大公因数的__________倍.18. 只含有素因数3的最小三位数是_________.19. 两个互素数的最小公倍数是108，则这样的数有_________________.20. 两个数的最大公因数是12，最小公倍数是180，这两个数是 .二、判断题：21. 因为a ÷b ＝3，所以a 是b 的倍数 （ ）22. 能同时被4、6整除的数，一定能被24整除 （ ）23. 任何正整数都至少有两个因数 （ ）24. 一个合数至少有三个因数 （ ）25. 三个连续的正整数的和可能是素数 （ ）26. 一个数能被2除尽，那么它一定是偶数 （ ）27. 两个数互素，那么它们没有相同的素因数 （ ）28. 两个偶数可能互素 （ ）29. 因为12÷6=2，所以说12是倍数，6是因数 （ ）30. 一个整数既没有最大的倍数，也没有最大因数 （ ）三、选择题：31. 在数0，1，2.5，43，2014，3.1415，-4中，非负整数的个数是（ ）。

1.已知10□8971能被13整除，求□中的数。

解：10□8-971=1008-971+□0=37+□0。

上式的个位数是7，若是13的倍数，则必是13的9倍，由13×9-37=80，推知□中的数是8。

2.判断18937能否被29整除；3.判断296416与37289能否被59整除。

解：（1）上述变换可以表示为：由此可知，296416能被59整除，37289不能被59整除4.九位数8765□4321能被21整除，求中间□中的数。

5.在下列各数中，哪些能被27整除？哪些能被37整除？1861026， 1884924， 2175683， 2560437，11159126，131313555，266117778。

6.在下列各数中，哪些能被19整除？哪些能被79整除？55119， 55537， 62899， 71258，186637，872231，5381717。

7.在下面的数中，哪些能被4整除？哪些能被8整除？哪些能被9整除？234，789，7756，8865，3728，8064。

解：能被4整除的数有7756，3728，8064；能被8整除的数有3728，8064；能被9整除的数有234，8865，8064。

8.在四位数56□2中，被盖住的十位数分别等于几时，这个四位数分别能被9，8，4整除？解：如果56□2能被9整除，那么5＋6＋□＋2＝13＋□应能被9整除，所以当十位数是5，即四位数是5652时能被9整除；如果56□2能被8整除，那么6□2应能被8整除，所以当十位数是3或7，即四位数是5 632或5672时能被8整除；如果56□2能被4整除，那么□2应能被4整除，所以当十位数是1，3，5，7，9，即四位数是5612，5632，5652，5672，5692时能被4整除。

9.五位数能被72整除，问：A与B各代表什么数字？分析与解：已知能被72整除。

因为72＝8×9，8和9是互质数，所以既能被8整除，又能被9整除。

第一讲数的整除一、整除1. 概念：对整数a、b、c，若a÷b=c 余0，则称a被b整除，或b整除a。

2. 特殊数的整除特征：被2、5整除；被4、25整除；被8、125整除；被3、9整除；被7、11、13整除二、因数和倍数1. 求一个数的因数，如12的因数有哪些？2. 一个数最小的因数是1，最大的因数是其本身。

3. 求因数个数，因数和4. 素数、合数、1（判断较大的数是素数还是合数，如667）5. 100以内的素数6. 分解素因数：短除法（分到出现素数，不可出现1）三、最大公因数、最小公倍数1. 方法：分解素因数法、短除法（分到互素，可出现1）2. 特殊性质：[M, N]×（M, N）=M×N3. 分数的最大公因数、最小公倍数四、余数定理和同余1. 余数定理：和/ 差/ 积的余数等于余数的和/ 差/ 积的余数2. 同余：几个数除以同一个数（M），若它们的余数相同，则这几个数关于该数（M)同余3. 同余特性：几个数关于某数同余，那么它们的差能被该数整除第二讲分数一分数1. 概念a/b→ a÷b → a:b(b≠0）2. 分类：真分数、假分数、带分数3. 假分数与带分数互化4. 性质：分数的分子、分母同时乘以（通分）或除以（约分）同一个不为0 的数，分数值不变5. 最简分数：分子分母互素二小数、分数互化1. 小数→分数（仅指小数部分）有限小数：看零位，一位小数十分之几，两位小数百分之几。

纯循环小数：一个循环节/ 循环节几个数几个"9"混循环小数：(所有数-不循环的数)/循环节几个数几个9，不循环的部分用0代注意：最后结果一定要化为最简分数2.分数→小数：分子÷分母分母只含因数2、5，化为有限小数分母只含因数非2、5，化为纯循环小数分母既含因数2、5，又含因数非2、5，化为混循环小数三分数的计算1. 加减：同分母，分母不变，分子相加减；异分母，先通分，再计算2. 乘除：乘法，分子×分子/分母×分母除法，除以一个数等于乘以它的倒数注意：带分数，加减法中一般拆成正整数+真分数乘除法中一般化为假分数乘除法中能约分先约分，再计算3. 运算定律：交换律，结合律，分配率4. 运算技巧：拆分：拆成相加：拆成几个数相加→约数法拆成两个数相加→裂项法拆成相减：裂项相消法换元法通项法5. 繁分数法一，将主分数线看成÷，分子÷分母法二，分子、分母同时乘以各小分母的最小公倍数。

预备年级数学第一章数的整除测试题07.9班级姓名学号得分一、填空：1、统称为自然数。

2、在正整数中，（有，没有）最大的数；（有，没有）最小的数；是。

3、把40分解素因数是。

4、6和8的公倍数（50以内）有。

5、6，10的最大公因数是，最小公倍数是。

6、10以内所有的素数的和是。

7、正整数a是正整数b的因数，a、b的最大公因数是，最小公倍数是。

8、试写出两个合数，使得它们互素。

（只需写出一组）9、一个数，千位是最小的奇数，百位是最小的合数，十位是最小的素数，个位是最小的自然数，这个数是。

10、A和B都是正整数，将它们分别分解素因数，得A=3×5×a，B=3×7×a，如果A和B的最小公倍数是315，那么a= 。

二、判断：11、两个奇数的和一定能被2 整除。

（）12、互素的两个数没有公因数。

（）13、把24分解素因数是 24=1×2×2×2×3 （）14、相邻两个正整数只有公因数1。

（）15、12 的因数有2、3、4、6 共4 个。

（）16、在正整数中，除了2以外，其余的素数都是奇数。

（）17、若两个数都是合数，则这两个数就不可能互素。

（）18、18的最大因数和最小倍数相等。

（）19、边长是正整数的正方形的周长一定是合数。

（）20、若甲数和乙数的最大公因数是b，则甲、乙两书都是b的倍数（）三、选择：21、在下面的式子里，表示整除的是 ( )（A）42÷0.7 = 60 （B）2.5÷5 = 0.5（C）48÷12 = 4 （D）12÷48 = 0.2522、在下列各组数中，互素的是（）（A）24和9 （B）8和9 （C）18和81 （D）17和5123、在算式15 = 3×5中，3和5是15的 ( )（A）素数（B）合数（C）公因数（D）素因数24、从323里至少减去（），才能被5整除。

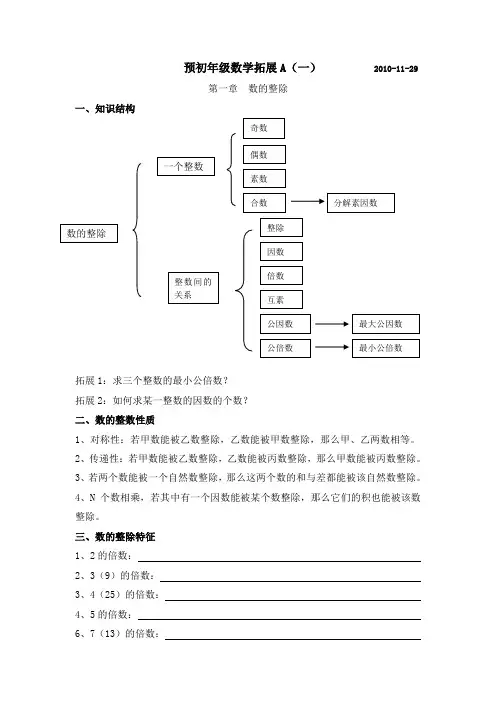
预初年级数学拓展A（一）2010-11-29第一章数的整除一、知识结构拓展1：求三个整数的最小公倍数？拓展2：如何求某一整数的因数的个数？二、数的整数性质1、对称性：若甲数能被乙数整除，乙数能被甲数整除，那么甲、乙两数相等。

2、传递性：若甲数能被乙数整除，乙数能被丙数整除，那么甲数能被丙数整除。

3、若两个数能被一个自然数整除，那么这两个数的和与差都能被该自然数整除。

4、N个数相乘，若其中有一个因数能被某个数整除，那么它们的积也能被该数整除。

三、数的整除特征1、2的倍数：2、3（9）的倍数：3、4（25）的倍数：4、5的倍数：6、7（13）的倍数：7、8（125）的倍数： 8、11的倍数：四、例题1、四位数57A1能被9整除，则A=2、六位数A8919B ，能被66整除，这个六位数是3、360的因数共有 个4、一个正整数被3除余1，被5除余3，被7除余5，这样的数中最小一个是5、学校组织学生跳绳比赛，进行分组，按每组6人、每组8人或每组10人分组，都余3人，问：共有多少学生参加参加比赛？6、任意一个三位数连着写两次得到一个六位数，这个六位数一定能同时被7、11、13整除，为什么？五、练习1、“校艺术节”上，预初年级同学要排练舞蹈，舞蹈老师要求除领舞1人外，其余的人要做队形变换，既能平均分成2组，又能平均分成3组，还能平均分成4组，那么至少需要多少名同学参加跳舞？2、某中学预初年级学生140人去上海科技馆参观，怎样租车合算？3、问：1260有多少个约数？4、一位青年司机（小于30岁）的年龄与他的出生月份和日期相乘正好是他的车牌号3325，问：这位司机生于何月何日？今年几岁？。

（4）非负整数是自然数。

（）（5）如果a能被b整除，那么a是b的倍数，b是a的因数。

（）7.乐乐家要装修新房子，地面是长3.2米、宽2.8米的长方形，准备用正方形的地砖铺满。

现有地砖尺寸是30×30、40×40（单位：厘米）的两种尺寸，你觉得用那一种比较合适，为什么？8.从下列数中选择适当的数填入相应的圈内：-25、13、 2.47、-8.75、0、29.自然数正整数负整数整数9.从下列算式中选择适当的算式填入相应的圈内：25÷5=5，2.5÷0.5=5，25÷3=8……1，25÷4=6.25整除除尽10.指出第一行的各数能被第二行的哪些数整除。

48 30 91 1202 3 5 78.三个素数的和为140，求这三个素数的乘积的最大值。

9.在1，2，3，…，2000这2000个自然数中，有 个自然数能同时被2和3整除，而且不能被5整除．10.五位数 是9的倍数，其中是4的倍数，那么的最小值是 ．11，有三个连续的自然数，它们的平均数能分别被三个不同的质数整除。

要使它们的和最小，这三个自然数分别是多少？,自我测试1，；两个数的最大公因数是1，最小公倍数是91，那么这两个数是 和 或 和 。

2，甲=A ⨯⨯52，乙=A ⨯⨯72，甲、乙两个数的最小公倍数是210，A 是 。

3，一个数减去2能被5整除，加上4能被6整除，这个数最小是几？4，由0，3，5写成的没有重复数字的三位数中，有哪些能被5整除？5，下面的连乘积中，末尾有多少个0？1×2×3×…×29×306，将1至9九个数字写在一条纸带上，如下图：将它剪成三段，每段上数字联在一起算一个数，把这三个数相加，使和能被77整除，那么中间一段的数是____。

（1998年全国小学数学奥林匹克决赛试题）。

整章综合测试第一组1-171、找出下列各句话中哪些是错的，并将其改正：（1）24的素因数有2，3；（2）10，22，25，30，48中能同时被2、5整除的数有10，30；（3）a与a+1一定互素；（4）0是整数但不是自然数。

2、用短除法求下列各组数的最大公因数：（1）24，36；（2）12，15，183、用短除法求下列各组数的最小公倍数：（1）30，45；（2）10，12，154、有一个四位数，它的四个数字中有两个是奇数，两个是偶数，两个是合数，两个是素数，而且两个合数不互素，两个奇数也不互素，四个数字从大到小排列，请问：这个四位数是多少？5、两个数的最大公因数是4，最小公倍数是24，已知其中一个数是12，求另一个数。

6、一个数去除16，24，32正好都能整除，则这个数最大是多少？7、有两个合数，而且互素，已知它们的最小公倍数是90，求这两个数。

8、三个素数，它们的乘积是1001，请你计算这三个素数各是多少？9、用3，4，0，5四个数字，按下列要求排成一个没有重复数字的四位数：（1）既能被2整除，又能被3整除；（2）能同时被2、3、5整除。

10、阅读课上，老师借来了24本科技类和18本人文类书籍，老师把这些书籍分成本数相等的科技、人文均有的若干组，每组中科技类和人文类书籍本数相等，请问：这些书籍最多分成几组？每组中各类书籍有几本？11、小明和小华两家是邻居，小明家每5天去超市购物一次，小华家每6天去同一家超市购物一次，中秋这天两家都去这家超市购物，那么再经过多少天他们又会在同一天都去超市购物？12、某校大约有80人至100人参加“3.12植树造林活动”，如果4人一组，6人一组，8人一组都恰好分完，那么全校参加植树造林活动的学生有多少人？13、阅读理解：例题：求1×2×3×4×5×…×29×30的积的末尾有几个连续的0.分析：因为2×5=10，所以只要含有一个素因数2和一个素因数5，乘积的末尾就有1个0，而这30个数中，素因数2的个数多于素因数5的个数，因此只要找素因数5的个数即可。

张江集团学校2014学年第一学期预初数学作业（5） 班级 学号 姓名 成绩 一、填空题： 1．如果m 是n 的倍数，那么m 、n 两数的最大公因数是 . 2．如果m 是n 的因数，那么m 、n 两数的最大公因数是 . 3．如果m 与n 互素，那么m 、n 两数的最大公因数是 . 4．如果m 、n 两数都是素数，那么m 、n 两数的最大公因数是 . 5．用一个数去除18和24，正好都整除，这个数最大是 . 6．如果两个数的积是12，最大公因数是2，那么这两个数是 . 7．如果两个数的最大公因数是10，那么为两个数的公因数有 . 8．已知a M ⨯⨯=32，a N ⨯⨯=72，如果N M ,两数的最大公因数是10， 那么=a . 二、解答题： 9．根据短除法计算并填空 A 和B 分别是 ； 这两个数的最大公因数是 . A 和B 的最大公因数是 .10．用短除法求下列各组数的最大公因数： （1）18和19 （2）29和58 （3） 18、12和 30 （4） 12、16和20 11．如果两个数的和是60，它们的最大公因数是15，那么这两个数分别是多少？ 12．一条街道如图所示，AB 长840米，BC 长720米，要在这条街道的一侧等距离地装上路灯，且要求两端和转弯处都必须装灯，那么这条街道最少要装多少盏灯？13．三种级别的茶叶，已知一级茶叶144克、二级茶叶180克、三级茶叶 240克的价格都是60元，现需要把三种茶叶分别按整数克装袋，要求每袋价格都相等，那么每袋价格最低是多少元？一、填空题：1．最小的素数与最小的合数的最小公倍数是．2．两个连续偶数的和是22，这两个偶数的最大公因数是，最小公倍数是．3．a、b都是正整数，如果a=3b，那么a、b的最小公倍数是.4．A=2×2×2×3×5，B=2×3×5×7，则A和B的最大公因数是，最小公倍数是.二、解答题：5．如图所示，根据短除法计算并填空Array①M是_______ ，②N是_______ ，③M、N最大公因数是_______ ，④M、N最小公倍数是_______ .6．求下列各组数的最大公因数和最小公倍数（1）60和126 （2）8、12和307．两个数的最大公因数是30，它们的最小公倍数是180，已知其中的一个数为90，求另一个数是多少？8．小明用一堆同样大小的长方形卡片摆出一个最小的正方形，已知卡片长12厘米，宽8厘米，则这个正方形的面积是多少平方厘米？9．桌上有一堆苹果，如果按8只、12只、16只一份来分都没有剩余，这堆苹果至少有多少只？10．甲、乙两人绕着圆形跑道同向跑步，甲跑一圈需要1分钟，乙跑一圈需要1分20秒.两人同时自起点出发，几分钟后两人在起点相遇？相遇时他们各跑了几圈？11．有一筐橘子，7个一数还多4个，5个一数又少3个，3个一数恰好数完，这筐橘子至少有多少个？。

张江集团学校2014学年第一学期预初数学作业（3）班级 学号 姓名 成绩一、判断题1．24和36相同的素因数是2，3。

（ ）2．如果c b a c b a , ,( =⨯都是正整数），那么c 一定是a 和b 的最小公倍数（ ） 3．两个数的最大公因数一定能被这两个数整除……（ ） 4．如果两个数互素，那么这两个数不可能都是合数（ ） 5．互素的两个数没有最大公因数….（ ） 二、填空题6．在数5，9，11，21，51，31，67，91中，素数有 . 7．84分解素因数是 。

8．两个数的最大公因数是1，最小公倍数是34，则这两个数是 . 9．一个数被2除余1，被3除余2，被5除余4，则这个数最小是_____________.10. 100以内， 和 既是素数，又是互素的两个相邻的自然数．11．n m ,和p 都是自然数，且12 ,2=÷=÷n m p n ，那么 ,n m 和p 的最大公因数是 ． 12．一个数的最小倍数是49，则这个数的所有因数有 ； 所有素因数有：13．能同时整除 2，3，5的最小正整数是 .14. a,b 都是自然数，5a b =⨯,那么a,b 的最大公因数是 ；最小公倍数是 . 15．m 是n 的倍数，且360m n ⨯=,m 和n 的最大公因数是6，则m= , n= . 16. 如果一个两位数不能被 整除，那么这个两位数一定是素数.17.已知2335A =⨯⨯⨯,223B =⨯⨯,那么A 和B 的最大公因数是 ，最小公倍数是 . 18．已知n A ⨯⨯=53，n B ⨯⨯=73的最小公倍数是210，则_______=n ，A 和B 的最大公因数是 ． 19．数a 和b 是两个相邻的自然数，且都是合数，那么它们的最大公因数是 ，最小公倍数是 ．20．任何一个两位数顺次写三遍，所得的六位数一定能被_____________这些不同的素因数整除. 21.规定一种新运算，对于一个合数n,（n ）表示不是n 的素因数的最小素数，如（4）=3，（12）=5，那么（60）+（84）= . 22.一筐苹果，一次拿2个，一次拿3个，一次拿4个，一次拿5个，都正好剩余1个，这筐苹果最少应有 个． 三、选择题：23．下列说法正确的是……………………………………………( ) (A) 最小的素数是1； (B) 自然数和负整数统称为整数；(C) 因为2.6 1.32÷=,所以2.6能被1.3整除； (D) 16的因数有2，4，8，16。

初一数学上册整除综合算式练习题整除是数学中一个重要的概念，它在解决问题时经常用到。

在初一的数学课上，我们学习了整除的相关知识，并进行了一些综合算式的练习。

本文将通过一些练习题来巩固和应用我们所学的整除知识。

1. 小明有一堆苹果，他想将这些苹果分成若干组，每组有6个苹果，正好分完。

如果小明有30个苹果，那么他可以分成几组？解析：我们可以将问题中的条件抽象为一个数学算式：30 ÷ 6 = 5。

即苹果的总数30除以每组苹果的个数6，得到的商5即为答案。

所以，小明可以分成5组。

2. 小华去超市买水果，他想买的苹果每盒有8个，香蕉每盒有6个，小华总共想买42个水果。

请问他至少要买几盒水果？解析：我们可以将问题中的条件抽象为一个数学算式：8x + 6y = 42。

其中，x代表苹果的盒数，y代表香蕉的盒数。

我们需要找到x和y的取值，使得方程成立。

通过尝试不同的取值，我们可以找到一个解：x = 3，y = 3。

所以，小华至少要买3盒水果。

3. 小红用苹果和香蕉制作了两种果汁，每种果汁需要的数量是相等的。

她有24个苹果和36个香蕉，请问她最多可以做几瓶果汁？解析：我们可以将问题中的条件抽象为一个数学算式：24x = 36x。

其中，x代表每种果汁所需的水果数量。

为了找到x的取值，我们可以将方程进行化简：24x - 36x = 0。

得到 -12x = 0，解方程得到x = 0。

这意味着小红无法制作果汁，因为每种果汁所需的水果数量为0。

所以，她最多可以制作0瓶果汁。

4. 平均而言，一个班级中有45个学生，这个班级共有苹果300个，香蕉240个，请问平均每个学生可以分到多少个苹果和香蕉？解析：我们可以将问题中的条件抽象为两个数学算式：300 ÷ 45 = 6.67，240 ÷ 45 = 5.33。

即苹果的总数300除以学生的个数45，得到平均每个学生分到的苹果数量约为6.67；香蕉的总数240除以学生的个数45，得到平均每个学生分到的香蕉数量约为5.33。

第一章 单元综合练习一．填空：1．在11÷5，2.1÷7，42÷14中，___能被___整除；___叫 ___的因数； ___叫 ___ 的倍数。

2．按要求填入相应圈内：20÷4 3 ÷0.5 7÷21 15÷60 90÷16 0.24÷0.08 56÷73．任何一个正整数都能被_____和______整除。

4．能同时被2、5整除的最大三位数是___________。

5．写出一个能被5除余3的三位数_______。

6．用5，7，8，0写出一个四位数，使它是2的倍数，最大是___________。

7．把下面各数填入适当的圈内：2，5，10，15，25，30，50．50的因数 5的倍数8．有一个数，它既是31的倍数，又是31的因数，这个数是__________。

9．102最多能被___个数整除，它们分别是___________________________。

10．用10以内三个不同的素数组成一个同时能被2、5整除的最大三位数是______。

11．两个素数的和是_________________________数。

12．___和___这两个数都是合数，又是互素数。

13．___和___这两个数都是素数，又是互素数。

14．___和___这两个数一个是合数，一个是素数，又是互素数。

15．所有是3的倍数，而不是2和5的倍数且小于50的两位数有_____________。

16．一个正方体的体积是1728立方厘米，则它的表面积是__________平方厘米。

二．判断题：1．36是倍数，4是因数。

（ ）2．10以内的偶数的平均数是4。

（ ）3．在57，5，97，1.5中，既是奇数又不是合数的数是57。

（ ）4．一个素数只有两个因数。

（ ）5．自然数中凡是3的倍数有偶数也有奇数。

（）6．偶数不一定是合数，奇数一定是素数。

预初（上）数学练习卷---数的整除与分数裂项一、填空题1、能整除6的数有________个；100的素因数是_________________。

2、互素的两个数的最小公倍数是216，并且这两个数都是合数，那么它们是__________。

2、秋游时要将全班24名女生和32名男生分成人数相等的若干组，每个小组的男生人数都相等，则全班最多能分成___________组。

3、既能被3整除，又能被5整除的三位数共有_ __个4、已知[]b a ,表示两个正整数b a 、的最小公倍数，如[]7035,14=，则满足[][]15,,6,==z y y x 的正整数有________组。

5、小明做作业的时候不小心在作业本上滴上了墨水，现在知道A 点表示的数是21，记B 点表示的数为x,那么x 的倒数是 ． 6、观察：;7151752,5131532,311312-=⨯-=⨯-=⨯那么直接写出下面的 计算结果：=⨯++⨯+⨯+⨯2013200911191951511 。

7、若水结成冰的题集增加了101，则冰化成水体积减少___________（填几分之几） 8、在31741 （）里，括号里应填什么自然数_________. 9、我们把分子为1的分数叫做单位分数. 如21，31，41…，任何一个单位分数都可以拆分成两个不同的单位分数的和，如21＝6131+，31＝12141+，41＝20151+，… （1）根据对上述式子的观察，你会发现51＝)(1)(1+.( 请在括号内填入合适的数)； （2）进一步思考，单位分数n 1（n 是不小于2的正整数）＝)(1)(1+，( 请在括号内填入合适的数) 10、与2614的乘积及与65172的乘积都是正整数的最小分数是___________. 11、如果x 是自然数，x 7是假分数，5x 是真分数，那么x 的取值有_________个。

12、如图，已知E 、F 、G 、H 分别是长方形ABCD 边上的4个点，且有=AF AB 73，AD AE 52=，BC CG 83=，DC CH 32=，那么三角形AEF 的面积占三角形CHG 面积的__________________（填几分之几）二、选择题1．下列说法中错误的是…………………………………………………（ ）（A ）如果整数a 是整数b 的倍数，那么b 是a 的因数；（B ）一个合数至少有3个因数；（C ）在正整数中，除2外所有的偶数都是合数；（D ）在正整数中，除了素数都是合数．2、在正整数中,关于2有如下四种描述(1)最小的奇数. (2) 最小的偶数. (3)最小的素数. (4)最小的合数. 其中说法正确的有…………………………………………………………( )A 、1个B 、2个C 、3个D 、4个3、．如果15a 是真分数，12a是假分数，那么满足条件的正整数a 有（ ）（A ）1个 （B ）2个 （C ）3个 （D ）4个4、．已知A 和B 二个数的因数情况如图所示,现有下列四种说法:（1）A 和B 都是偶数；（2）A 和B 的最大公因数是8；（3）A 和B 公有的素因数是1；（4）A 和B 的最小公倍数是96．请问其中说法正确的有（ ）种。

数学综合算式练习题数的整除性质数学是一门抽象而又实用的学科，其中算式练习题是培养学生数学思维和解决问题能力的重要方法之一。

在解答算式练习题时，学生不仅需要熟练掌握数的性质，更需要理解数的整除性质。

本文将通过一些具体的练习题，探讨数的整除性质在算式中的应用。

一、整除性质的概念在开始解答练习题之前，我们先来回顾一下整除性质的概念。

对于任意两个正整数a和b，如果存在一个整数k使得a=k*b，我们就说b整除a，记作b|a。

其中，a被称为被除数，b被称为除数，k被称为商。

整除性质是数的基本性质之一，它描述了两个数之间的一种特殊关系。

二、整除性质在算式中的应用2.1 乘法的整除性质我们先来看一个例子：如果10整除25，那么下面哪个算式成立？A. 10*(2+3) = 2*(2+5)B. 10*(2+3) = 2*(2+6)C. 10*(2+3) = 2*(2+7)通过观察可知，10整除25，即10是25的因数。

根据乘法的整除性质，如果一个数整除另一个数，那么这两个数的乘积也一定能被这个数整除。

根据这个性质，我们可知A选项成立，即10*(2+3)能整除2*(2+5)。

2.2 除法的整除性质接下来我们看一个关于除法的例子：已知36能被整除的数是1、2、3、4、6、9、12、18、36，只需用4个不同的数字填空：①__ ×②__ ÷③__ = 36 ÷④__。

我们可以根据36的因数和除法的整除性质来进行推理。

由于36能被2整除，那么①的值就是2。

同理，由于36能被9整除，那么③的值就是9。

根据36÷④__的结果是整数，我们可知④的值只能是1。

于是，将2×36÷9=36÷1得到的等式是成立的。

2.3 加法的整除性质最后我们来看一个加法的例子：小明将两个数相加后得到28，其中较小的数能被5整除，较大的数能被7整除。

这两个数分别是多少？根据加法的整除性质，如果一个数能被两个数整除，那么这个数的倍数也能被这两个数整除。