4等差等比数列综合(JT)
- 格式:docx
- 大小:13.40 KB
- 文档页数:4

等比等差混合数列求和
摘要:
一、等比等差混合数列求和的概念
二、等比等差混合数列求和的公式
三、等比等差混合数列求和的实例与解析
四、总结与拓展
正文:
一、等比等差混合数列求和的概念
等比等差混合数列求和,是指在等比数列与等差数列相混合的情况下,求出该数列和的一种方法。
等比数列具有公比性质,等差数列具有公差性质,当这两种数列混合在一起时,我们需要分别考虑它们的性质,进而求出总和。
二、等比等差混合数列求和的公式
在等比等差混合数列求和中,我们需要先分别找出等比数列和等差数列的通项公式,然后将它们相加。
设等比数列的首项为a,公比为r,等差数列的首项为b,公差为d,项数为n,则等比等差混合数列的通项公式为:an = a * r^(n-1) + b + (n-1) * d。
求和公式为:S_n = (a * (1 - r^n)) / (1 - r) + n *
(b + b + (n-1) * d) / 2。
三、等比等差混合数列求和的实例与解析
例如,我们有一个等比等差混合数列:3, 6, 9, 12, 15。
我们可以先观察到这是一个等差数列,公差为3,然后再观察到它是一个等比数列,公比为2。
我们可以根据求和公式计算出这个数列的和为:S_5 = (3 * (1 - 2^5)) / (1 - 2)
+ 5 * (6 + 6 + (5-1) * 3) / 2 = 45。
四、总结与拓展
等比等差混合数列求和是一种基本的数学计算方法,它在实际生活中也有很多应用,比如在金融、统计等领域。
对于这类问题,我们需要掌握相关的公式,并能熟练地运用它们来解决问题。


等差数列与等比数列综合应用知识点一. 等差、等比数列综合问题:只要把条件转化基本量d a ,1或q a ,1的关系,再通过解方程找出关系求解。
1..数列{}n a 的通项n a 与前n 项和n S 的关系:⑴n n a a a S +++= 21; ⑵ ()⎩⎨⎧≥-==-2)1(11n S S n S a n nn .2..两个重要变形:()2≥n⑴ ()()()123121--++-+-+=n n n a a a a a a a a ; ⑵123121-⨯⨯⨯⨯=n n n a a a a a a a a . 3数列求和问题:⑴ 分组求和:问题分为等差数列和等比数列两组,(或两组等差数列) ,(或两组等比数列) 利用公式求和。
⑵ 裂项相消求和:求和式是分式的一般先把通项裂项分开,再把求和式的每一项都裂项,于是中间的项都互相抵消,剩下头尾的“对称”的项,即前面剩几项,后面也剩几项。
如:()11111+-=+=n n n n a n ,()11321211+++⨯+⨯=n n S n 1111113121211+-=⎪⎭⎫ ⎝⎛+-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=n n n ⑶ 错位相减求和:求和式是等差数列与等比数列的乘积的,求和方法是求和式两边乘公比后再两式相减,转化为等比数列求和化简可得。
如:12-⋅=n n n a ,12102232221-⋅++⋅+⋅+⋅=n n n S ,…① 两边同乘公比2=q 得: ()n n n n n S 22123222121321⋅+⋅-++⋅+⋅+⋅=- …② 于是①-②得:n nnn n n n S 221212222112⋅---=⋅-++++=-- ,∴()121122+-=+-⋅=n n n n n n S4.数列的应用问题:对于数列的应用题,一是要分清是等差数列还是等比数列,即它们的首项,公差或公比是什么;二是求某一项还是求和。
例1: (1)数列{}n a 的通项是()()12121+-=n n a n ,则其前n 项和为nS ___=析:∵()()12121+-=n n a n ⎪⎭⎫ ⎝⎛+--=12112121n n ,裂项求和:∴12121121121121513131121+=⎥⎦⎤⎢⎣⎡+-⨯=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⨯=n n n n n S n(2)求和:nn n S 21813412211++++= . .析:(3)()()211211212121412121-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯++=⎪⎭⎫ ⎝⎛+++++++=n n nn n n S nn n ⎪⎭⎫ ⎝⎛-++=21122(4) nn n S 21813412211⨯++⨯+⨯+⨯=析:n n n S 2121321221132⨯++⨯+⨯+⨯= ,132212122112+⨯++⨯+⨯=n n n S 两式相减得:111322211221121121221212121+++-⎪⎭⎫⎝⎛-=--⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯=-++++=-n nn nn n n n n nS∴12211+++-=n n n n S (5)错误!未找到引用源。

等差等比数列的综合及数列求和知识要点:1、等差数列、等比数列的综合 (1)等差数列通项公式有如下求法:a a d a a d a a d n n N n n n 213211212-=-=-=-∈≥-…()…()………,且()()()()()dn a a n n 11211-=--+++有,…∴()a a n d n =+-11当()()n a n d a n N a a n d n =+-=∈=+-111111时,知,,成立。
由此,这种“累加法”适用于如下数列{}a n :()a a f n n n +-=1的数列求通项公式。
(2)等比数列通项公式有如下求法:a a q a a q a a q n n N n nn 213211212===-∈≥-…()…()………,且()()()()12111⨯⨯⨯-=-……,得n a a q nn∴·a a q n n =-11 当n a q a n N a a q n n n ==∈=--111111时,·,知,·成立。
由此,这种“累乘法”知用于如下数列{}a n ,()a a g n n n+=1的数列求通项公式。
(3)“错位相减法”求“差比数列”的前n 项和 等比数列前n 项和公式采用的是“错位相减法”求得,用此方法还可以求符合条件的“差比数列”求前n 项和:a b C n n n =·,其中{}b n 是等差数列,{}C n 是等比数列,公差为d ,公比为q ()q ≠1。
设S a a a n n =+++12… =+++b C b C b C n n 1122··…·……(1) 两边同乘以q ,得qS b C q b C q b C q n n n =+++1122··…·=+++b C b C b C n n 12231 (2)(1)-(2),得:()()()()()()1112212231112121111231-=+++-+++=+-++--=++++-+-++q S b C b C b C b C b C b C b C b C C b b C b C b C d C C C b C n n n n n n n n n n n n n …………∴()[]S b C q dq C q C q qb n d C q n n n =-+----+-1111111111··· 2、数列求和求()S a a a f n n n =+++=12…的方法有如下几种 (1)公式法:等差数列中()()S na n n dn a a n n =+-=+11122等比数列中()()()S na q a a q qa q q q n nn ==--=--≠⎧⎨⎪⎩⎪11111111()()121216222+++=++…n n n n(2)错位相减法:如果一个数列的通项是由一个等比数列相应项乘积构成其前n 项和公式可以采用“错位相减法”求得。

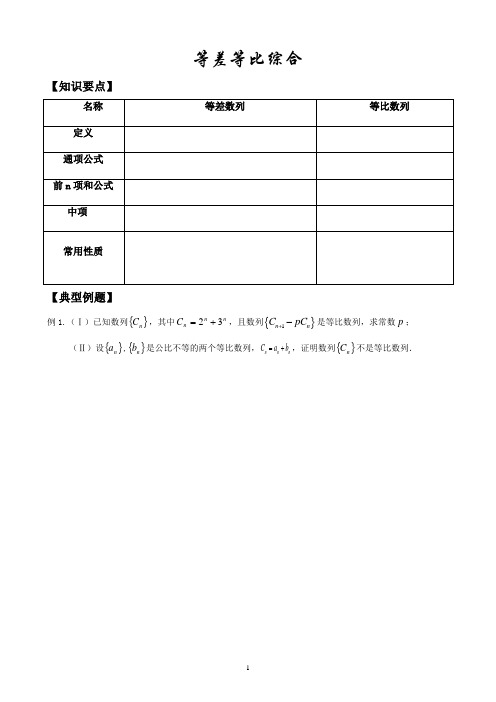
等差等比综合【知识要点】名称 等差数列等比数列定义 通项公式 前n 项和公式 中项常用性质【典型例题】例1.(Ⅰ)已知数列{}n C ,其中nn n C 32+=,且数列{}1n n C pC +-是等比数列,求常数p ;(Ⅱ)设{}n a ,{}n b 是公比不等的两个等比数列,n n n b a C +=,证明数列{}n C 不是等比数列.例2. 在等比数列{n a }中,111000,,10a q ==又设121(lg lg ...lg )n nb a a a n=++.求数列{n b }的前n 项和的最大值.例3.已知数列{n a }中,n S 是它的前n 项和,并且*1142(),1n n S a n N a +=+∈= (1) 设12(*)n n n b a a n N +=-∈求证:数列{}n b 是等比数列; (2) 设*()2n n na C n N =∈,求证:数列{}n c 是等差数列;例4.已知{}n a 是各项为不同的正数的等差数列,421lg ,lg ,lg a a a 成等差数列,又,...3,2,1,12==n a b nn(1)证明{}n b 为等比数列; (2)如果数列{}n b 前3项的和等于724,求数列{}n a 的首项1a 和公差d例5.已知数列{}n a 满足,12211,3,32()n n n a a a a a n N *++===-∈(1)证明数列{}1n n a a +-是等比数列;(2)求数列{}n a 的通项公式 (3)若数列{}n b 满足1211144...4(1)()n n b bb b n a n N ---*=+∈,证明{}n b是等差数列【课堂训练及作业】1.如果821a ,...a ,a 为各项都大于零的等差数列,公差0d ≠,则( )A .5481a a a a >B .5481a a a a <C .5481a a a a +>+D .5481a a a a =2.(2006年北京卷)设4710310()22222()n f n n N +=+++++∈ ,则()f n 等于( )A .2(81)7n-B .12(81)7n +- C .32(81)7n +- D .42(81)7n +-3.在各项都为正数的等比数列{}n a 中,首项,3a 1=前三项和为21,则=++543a a a ( )A .33B .72C .84D .1894.已知数列的通项公式为49n 2a n -=,则n S 达到最小值时,n=( )A .26B .25C .24D .235.设数列{}n a 和数列{}n b 是等差数列,其中100,75,2510010011=+==b a b a 且则数列{}n n b a +的前100项之和是 ( )A.0B.100C.10000D.15050006.在11+n n与之间插入n个数,使这2+n 个数依次成等比数列,则插入的这n 个数的积等于 .7.在数列{}n a 中,,2a ,1a 21==且)N n ()1(1a a n n 2n *+∈-+=-,则=100S 8.数列{}n a 前n 项和为n S ,且,...2,1n ,S 31a ,1a n 1n 1===+,求(1)的432a ,a ,a 值及数列{}n a 的通项公式 (2)24a a +62n +a +...+a 的值。
数列、极限、数学归纳法——等差、等比数列综合问题教案一、教学目标1. 知识与技能:(1)理解等差数列和等比数列的定义及其性质;(2)掌握数列的极限概念,并能应用于等差、等比数列;(3)学会使用数学归纳法证明与数列相关的问题。
2. 过程与方法:(1)通过实例分析,培养学生的观察、思考和解决问题的能力;(2)运用数列极限的概念,解决实际问题,提高学生的数学应用能力;(3)引导学生运用数学归纳法证明数列相关问题,培养学生的逻辑推理能力。
3. 情感态度与价值观:(1)培养学生对数学的兴趣,提高学习数学的积极性;(2)培养学生勇于探索、严谨治学的科学精神;(3)通过小组合作、讨论,培养学生的团队协作能力。
二、教学重点与难点1. 教学重点:(1)等差数列和等比数列的定义及其性质;(2)数列极限的概念及应用;(3)数学归纳法的步骤及应用。
2. 教学难点:(1)数列极限的求解方法;(2)数学归纳法的证明过程及逻辑推理。
1. 导入新课:通过生活中的实例,如等差数列“1, 3, 5, 7, ”和等比数列“1, 2, 4, 8, ”,引发学生对数列的兴趣,引入本节课的主题。
2. 知识讲解:(1)等差数列和等比数列的定义及其性质;(2)数列极限的概念及其在等差、等比数列中的应用;(3)数学归纳法的步骤及其在数列相关问题中的应用。
3. 例题解析:选取具有代表性的例题,引导学生运用所学知识解决问题,巩固课堂内容。
4. 课堂练习:布置一些有关等差、等比数列及数列极限的练习题,让学生课后巩固所学知识。
四、课后作业1. 复习课堂内容,整理学习笔记;2. 完成课后练习题;3. 预习下一节课内容。
五、教学评价1. 课堂表现:观察学生在课堂上的参与程度、提问回答等情况,了解学生的学习状态;2. 课后作业:检查学生作业完成情况,评估学生对课堂内容的掌握程度;3. 单元测试:进行阶段测试,了解学生对等差、等比数列及数列极限知识的综合运用能力。
等差等比综合【知识要点】【典型例题】例1.已知数列{}n a 的前n 项和()2*202n S n n n N =-∈,求数列{}n a 的前n 项的和n T 的表达式.例2.设首项为正数的等比数列,它的前n 项之和为80,前n 2项之和为6560,且前n 项中数值最大的项为54,求此数列例3.已知等比数列的前10项中,所有奇数项之和为4185,所有偶数项之和为21170,求12963a a a a S +++=的值.例4. 在等比数列{n a }中,111000,,10a q ==又设121(lg lg ...lg )n n b a a a n=++.求数列{n b }的前n 项和的最大值.例5.已知数列{n a }中,n S 是它的前n 项和,并且*1142(),1n n S a n N a +=+∈=(1) 设12(*)n n n b a a n N +=-∈求证:数列{}n b 是等比数列; (2) 设*()2n n n a C n N =∈,求证:数列{}n c 是等差数列;例6.已知{}n a 是各项为不同的正数的等差数列,421lg ,lg ,lg a a a 成等差数列,又,...3,2,1,12==n a b nn (1)证明{}n b 为等比数列; (2)如果数列{}n b 前3项的和等于724,求数列{}n a 的首项1a 和公差d【课堂训练及作业】1.如果821a ,...a ,a 为各项都大于零的等差数列,公差0d ≠,则( ) A .5481a a a a > B .5481a a a a < C .5481a a a a +>+D .5481a a a a =2.已知等差数列{}n a 的公差为2,若431a ,a ,a 成等比数列,则2a = ( ) A .-4B .-6C .-8D .-103.在各项都为正数的等比数列{}n a 中,首项,3a 1=前三项和为21,则=++543a a a ( ) A .33B .72C .84D .1894.已知数列的通项公式为49n 2a n -=,则n S 达到最小值时,n=( ) A .26 B .25C .24D .235.首项为0的等差数列{}n a 的前n 项和为n S ,则n n a S 与的关系为( ) A .n n a 2nS =B .n n na S =C .n n a S =D .n 2n a n S =6. 已知数列{}n a 中,⎩⎨⎧-=-)n (1n 2)n (2a 1n n 为正偶数为正奇数,则9a = ,设数列{}n a 前n 项和为n S ,则=9S7.在数列{}n a 中,,2a ,1a 21==且)N n ()1(1a a nn 2n *+∈-+=-,则=100S8.已知数列{}n b 为等差数列,它的首项11b =,前10项的和为55,令*2log ()n n b a n N =∈.求满足12100n a a a +++≥的最小正整数n .。
菁差菁比探合
【知识要点】
【典型例题】
例1.已知数列@}的前〃项和S”=20〃-灯(心M),求数列仏|}的前“项的和7;的表达式.
例2•设首项为正数的等比数列,它的前"项之和为80,前2“项之和为6560,且前九项中数值最大的项为54,求此数列.
例3.已知等比数列的前10项中,所有奇数项之和为851,所有偶数项之和为170?,
求 S = “3 + “6 + 5 + a\2的值・
例4.在等比数列{5 }中,4 =1000.9 =丄,又设乞=-(lg«i +lg«2 +・・・lg©)・求数列{" }的
前n项和的
10 n
最大值.
(1)设b n=a n^-2a n(neN*)求证:数列{$}是等比数列:
⑵ 设C“= *(“€”),求证:数列{c”}是等差数列;
2
例6.已知{〜}是各项为不同的正数的等差数列,lgglgglg^成等差数列,又仇=丄/ = 1,2,3,...
(1)证明{$}为等比数列;
7
(2)如果数列{b fI}前3项的和等于—,求数列{© }的首项⑷和公差d
【课堂训练及作业】
1. 如果a p a 2,...a s 为各项都大于零的等差数列,公差dHO,则()
2. 已知等差数列{〜}的公差为2,若a p a 3,a 4成等比数列,则a 2 = ()
A ・ 一4 B. 一 6 C. 一 8 D ・ 一 10
3. 在各项都为正数的等比数列&}中,首项a, =3,前三项和为21,则as +a 4+a 5 = ()
A. 33 B ・ 72 C. 84 D ・ 189
4. 已知数列的通项公式为a. =2n-49,则S.达到最小值时,n=()
A ・26
B ・25
C ・24
D ・23
5. 首项为0的等差数列{“”}的前n 项和为Sn ,则Sn 与a“的关系为( )
A ・ S n =—a n B. S n = na n C. S n =a n D ・ S n = ira n
7. 在数列{-}中,3|=1宀=2,且a n +2—a rl =l + (—l)n (nwN ・),则S I00 = ______________
8. 已知数列{$}为等差数列,它的首项勺=1,前]0项的和为55,令化=log 2 a n (n e N 、•求满足 a } +a 2 +・•• + % > 100的最小正整数n.
已知数列仏}中,a n =<
2n -'(n 为正奇数) 2n-l(n 为正偶数)。