立体图形的表面积和体积

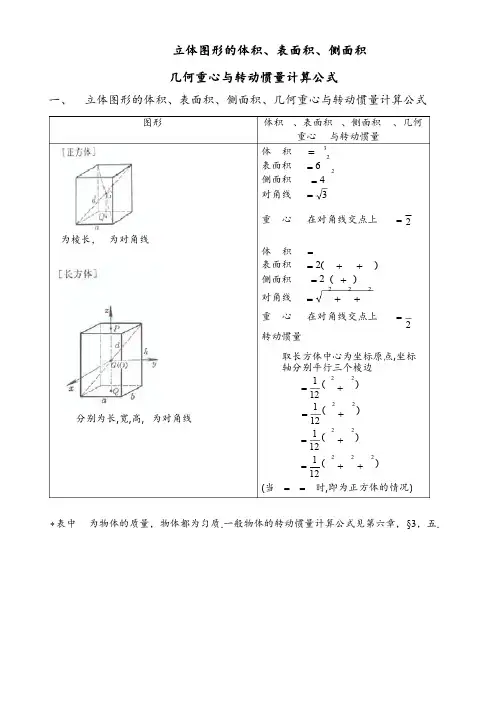
立体图形的体积、表面积、侧面积几何重心与转动惯量计算公式一、 立体图形的体积、表面积、侧面积、几何重心与转动惯量计算公式图形 体积、表面积、侧面积、几何重心与转动惯量为棱长，为对角线分别为长,宽,高,为对角线体 积 3=表面积26=侧面积24=对角线 3=重 心 在对角线交点上2=体 积 =表面积 )(2++=侧面积 )(2+=对角线222++=重 心 在对角线交点上2= 转动惯量取长方体中心为坐标原点,坐标轴分别平行三个棱边)(12122+=)(12122+=)(12122+=)(121222++= (当==时,即为正方体的情况)*表中为物体的质量，物体都为匀质.一般物体的转动惯量计算公式见第六章，§3，五.图形 体积、表面积、侧面积、几何重心与转动惯量为边长,为高为底边长,为高,为对角线为棱数,为底边长,为高,为斜高 体 积 =表面积 +=2侧面积 )(++=式中为底面积重 心2=(、分别为上下底重心)转动惯量对于正三棱柱()取为坐标原点,轴与棱平行1248324==体 积 225981.2233»=表面积61962.563322+»+= 侧面积 6=对角线224+=重 心2=(、分别为上下底重心)转动惯量取为坐标原点,轴与棱平行12583524==体 积 31=表面积 +=侧面积2'==式中为底面积,'为一侧三角形面重 心4h GQ = (Q 为底面的重心)图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量Ja,b,c,p,q,r 为棱长h 为高体积 011111010101028812222222222222c b ac p qb p r a q r V = 重心PQ GQ 41= (P 为顶点,Q 为底面的重心)体积)''(3FF F F h V ++=式中F F ,'分别为上下底面积重心 '''3'24FF F F F FF F PQ GQ ++++=(P ,Q 分别为上下底重心)分别为上下底边长,为棱数,为高,为斜高体 积÷÷øöççèæ÷øöçèæ++=2''13表面积 ++='侧面积 )'(2+=式中,'分别为上下底面积重 心2222'''3'24++++= (、分别为上下底重心)图形 体积、表面积、侧面积、几何重心与转动惯量两底为矩形,分别为上下底边长,为高,1为截头棱长体积]'')')('([6++++= '''1--=重心''2''2''3''2++++++= (分别为上下底重心)底为矩形,a,b为其边长,h为高,a’为上棱长r为半径 重心'2'2aaaaPQGQ++=(P为上棱中点,Q为下底面重心)体 积33352360.0634ddrV»==pp 表面积24rS p=重 心 G与球心O重合转动惯量取球心O为坐标原点mrJJJzyx252===mrJo253=图形 体积V、表面积S、侧面积M、几何重心G与转动惯量J[半球体]r为半径,O为球心r为球半径,a为弓形底圆半径,h为拱高,a为锥角(弧度)r为球半径,a为拱底圆半径,h为拱高 体 积 331232drVpp==表面积23rS p=侧面积22rM p=重 心 rGO83=转动惯量取球心O为坐标原点,z轴与GO重合 mrJJJzyx252===mrJo253=体 积 hrhrV220944.232»=p表面积 )2(ahrS+=p侧面积 (锥面部分) rM pa=重 心 )2(83hrGO-=转动惯量z轴与GO重合úûùêëé-÷øöçèæ-=2sin2cos2cos1215225aaap rJz÷øöçèæ+-=2cos2cos32533aahmr体 积)3(3)3(6222hrhhahV-=+=pp表面积 )2()2(222aharhS+=+=pp 侧面积(球面部分))(222harhM+==pp重 心)3()2(432hrhrGO--=图形 体积V、表面积S、侧面积M、几何重心G与转动惯量J[球台]r为球半径,a¢,a分别为上下底圆的半径,h为高R为中心半径,D为中心直径,r为圆截面半径,d为圆截面直径体 积 )'33(6222haahV++=p表面积 )'2(22aarhS++=p侧面积 rhM p2=2222222'÷÷øöççèæ--+=hhaaar重 心22244'33'23haaaahGO++-=222222'33'422haahaahGQ++++=(Q为下底圆心)体 积 222242DdRrVpp==表面积 DdRrS224pp==重 心 G在圆环的中心上转动惯量取圆环的中心为坐标原点,z轴垂直于圆环所在平面mRrJJyx÷÷øöççèæ+==28522mRrJz÷øöçèæ+=2243图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量J [圆柱体]r 为底面半径,h 为高R 为外半径,r 为内半径,h 为高r 为底圆半径,h,H 分别为最小,最大高度,a 为截角,D 为截头椭圆轴体 积h r V 2p = 表面积)(2h r r S +=p 侧面积rh M p 2= 重 心 2hGQ =(P ,Q 分别为上下底圆心) 转动惯量 取重心G 为坐标原点,z 轴垂直底面m h r J J y x ÷øöçèæ+==34122m r J z 22=体 积th R r R h V p p 2)(22=-= 表面积 )(222r R M S -+=p侧面积 R h r R h M p p 4)(2=+= 式中t 为管壁厚,R 为平均半径重 心2h GQ = 转动惯量 取z 轴与GQ 重合 m r R J z 2)(22+=体 积 )(22h H r V +=p 表面积 ÷øöçèæ++=a p cos 112r M S ÷øöçèæ+++=2D h H r r p 侧面积 )(h H r M +=p 截头椭圆轴22)(4h H r D -+= 重 心tan 22r h H +a)(2tan 2h H r GK +=a (GQ 为重心到底面距离,GK 为重心到轴线O O ¢的距离)图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量Jh 为截段最大高度,b 为底面拱高,2a 为底面弦长,r 为底面半径,a 2为弧所对圆心角(弧度)体 积])(3)3([3222a r b r a r a bh V -+-=÷øöçèæ--=a a a cos sin 31sin 33a b hr侧面积(柱面部分)])[(2a r b b rhM +-=a体 积abc abc V 1888.434»=p 重 心G 在椭球中心O 上 转动惯量 取椭球中心为坐标原点,z 轴与c 轴重合m c b J x )(5122+=m a c J y)(5122+= m b a J z)(122+=a,b,c 为半轴图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量J体 积h r V 23p= 表面积 )(l r r S +=p 侧面积 rl M p = 母 线 22h r l +=重 心4h GQ = (Q 为底圆中心,O 为圆锥顶r为底圆半径,h为高,l为母线r,R分别为上,下底圆半径,h为高,l为母线上下底平行,F¢,F分别为上,下底面积,F为中截面面积,h为高取圆锥顶点为坐标原点,z轴与GQ 重合mhrJJyx÷÷øöççèæ+==22453mrJz2103=体 积 )(322RrrRhV++=p表面积 )(22rRMS++=p侧面积 )(rRlM+=p母 线22)(hrRl+-=圆锥高(母线交点到底圆的距离)rRhrhH-+=重 心2222324rRrRrRrRhGQ++++=(P,Q分别为上下底圆心)体 积 )4'(60FFFhV++»[注] 棱台、圆台、球台、圆锥、棱柱、圆柱等都是拟棱台的特例图形 体积V、表面积S、侧面积M、几何重心G与转动惯量Jd 为上,下底圆直径,D 为中截面直径,h 为高母线为圆弧时: 体积)2(26180.0)2(122222d D h d D hhV +»+=p2)2(08727.0d D h +»母线为抛物线时: 体积 ÷øöçèæ++=2243215d Dd D h V p )348(05236.022d Dd D h ++» 重心2h GQ = (P ,Q 分别为上下底圆心)二、 多面体[正四面体] [正八面体] [正十二面体] [正二十面体]图形面数f4 8 12 20 棱数k 6 12 30 30 顶点数e 462012体积V 31179.0a34714.0a36631.7a31817.2a表面积S27321.1a24641.3a26457.20a26603.8a表中a 为棱长.[欧拉公式] 一个多面体的面数为f ，棱数为k ，顶点数为e ,它们之间满足 2=+-f k e。

教育学科教师辅导讲义学员编号： 年 级： 课 时 数： 学员姓名： 辅导科目： 学科教师： 授课 类型T (立体图形相关知识点) C （典型例题试题讲解） T （拓展提高）授课日期时段教学内容知识点一：表面积1、长方体表面积=长x 宽× 2+ 宽× 高× 2+ 长×高× 2 字母公式：S=ax b× 2+ a× c× 2+ b×c× 2 或者：长方体的表面积 =( 长×宽 + 长×高 + 宽×高 ) × 2 。

字母公式：S=(ax b+ a× c+ b×c)× 22、正方体的表面积 =棱长×棱长×6。

字母公式：S=a ×a× 63、圆柱体的表面积：圆柱表面积=上底+下底+侧面（侧面面积=底面圆的周长×圆柱的高） 用字母表示：22s r ch π=+注：侧面积的求法：已知底面半径和高，rh π侧2s = 已知底面直径和高，dh π侧=s知识点二：体积1、长方体体积：长方体体积= ① 长×宽×高 （Ｖ＝ａｂｈ）② 底面积×高=横截面积×长 （V =sh ） 2、正方体的体积：正方体体积＝棱长×棱长×棱长检测题1：把一个圆柱的侧面展开，得到一个正方形．已知这个圆柱的高是10厘米，它的侧面积是（ ）平方厘米．A ．50B ．100C ．50πD ．100π答案：B检测题2．把一个棱长4厘米的正方体分割成两个长方体，表面积增加了______平方厘米．答案：64检测题3 一个正方体的棱长之和是48厘米，它的棱长是______厘米，表面积是______平方厘米，体积是______立方厘米． 答案：2 24 8检测题4 把两个棱长5厘米的正方体拼成一个长方体，这个长方体的表面积是______平方厘米．答案：250检测题5．一个练功房铺设了1600块长50厘米，宽10厘米，厚3厘米的木地板，这个练功房的面积有______平方米．答案：这个练功房的面积有80平方米．检测题6．圆柱的底面半径扩大2倍，高缩小到原来的21，它的体积就（ ）答案：扩大2倍检测题7．做一个圆柱体，侧面积是9.42平方厘米，高是3厘米，它的底面半径是______．答案：1.57cm一、专题精讲例1.如图是高为10厘米的圆柱，如果它的高增加4 厘米，那么它表面积就增加125.6平方厘米。

立体图形的表面积与体积立体图形是我们常见的一种几何图形，它具有三个维度：长度、宽度和高度。

对于一个立体图形来说，其表面积和体积是两个重要的参数。

本文将详细介绍立体图形的表面积与体积的计算方法及其应用。

一、立体图形的表面积计算方法立体图形的表面积是指该图形所有面积之和。

不同类型的立体图形，其表面积计算公式也不同。

下面我们将逐一介绍几种常见立体图形的表面积计算方法。

1. 立方体的表面积计算公式立方体是最简单的一种立体图形，其所有面都是正方形。

设立方体的边长为a，则立方体的表面积S为S = 6a^2。

2. 正方体的表面积计算公式正方体的所有面同样是正方形。

设正方体的边长为a，则正方体的表面积S等于立方体的表面积，即S = 6a^2。

3. 圆柱体的表面积计算公式圆柱体包括一个底面和一个侧面。

设底面的半径为r，圆柱体的高度为h，则圆柱体的表面积S = 2πrh + πr^2。

4. 圆锥体的表面积计算公式圆锥体包括一个底面和一个侧面。

设底面的半径为r，圆锥体的高度为h，则圆锥体的表面积S = πrl + πr^2，其中l为圆锥体的斜高。

5. 球体的表面积计算公式球体是一种特殊的立体图形，其表面由无数个点组成。

设球体的半径为r，则球体的表面积S = 4πr^2。

二、立体图形的体积计算方法立体图形的体积是指该图形所包围的三维空间的大小。

与表面积一样，不同类型的立体图形的体积计算公式也各不相同。

下面我们将介绍几种常见立体图形的体积计算方法。

1. 立方体的体积计算公式立方体的体积计算最简单，其体积V等于边长的立方，即V = a^3。

2. 正方体的体积计算公式正方体的体积与立方体相同，即V = a^3。

3. 圆柱体的体积计算公式圆柱体的体积V等于底面积乘以高度，即V = πr^2h。

4. 圆锥体的体积计算公式圆锥体的体积V等于底面积乘以高度再除以3，即V = (1/3)πr^2h。

5. 球体的体积计算公式球体的体积V等于4/3乘以π乘以半径的立方，即V = (4/3)πr^3。

立体图形的表面积和体积芝川小学：鱼继华一、教材依据：人民教育出版社义务教育课程标准实验教科书第十二册第六单元第二小节空间与图形中图形的认识与测量中例4.教科书第98页。

二、设计思路：1、指导思想：为了体现本课的设计理念我构建了学生自主学习的基本教学模式：设疑激趣——引导回顾——应用提高——交流评价通过认真分析教材，贯彻新课标精神，并结合六年级学生的特点，我设计了以下教学方法：1、启发式教学法，六年级学生已经有了一定的独立思考和学习的能力，应用启发式教学，可以充分调动学生的自主能力，给学生一定的思维空间，提高他们的学习兴趣。

在教学中多采用启发式提问，给学生指明方向、，让他们自己去寻找答案。

比如在教学什么是体积时给出提示问题，让他们思考，自己去解决。

2、实验演示法，这是一种最直观、形象的教学方法，对学生的学习最有帮助。

让学生说出书的不同包装方法，我随机展示，让学生观察、比较，从而得出最科学的包装方法。

3、巩固练习法，通过练习熟练知识，形成技能。

在练习作业中我设计了不同的题型，帮助学生巩固各种图形的计算方法。

从而突出重点，突破难点。

同时广泛的练习也培养了学生的主动参与意识。

达尔文说过：最有价值的知识是方法的知识。

现代教育要注重数学学习的情感化，活动化，自主化。

给学生一些权利，让他们自己去选择：给学生一些机会，让他们自己去探索；给学生一些空间，让他们自己去发现。

因此在教学中我把主动权交给学生，放手让他们通过小组活动，操作实践，认真观察，自主探索，合作交流等有效的学习方法主动的进行学习。

这样学生学的积极，老师也教的轻松。

2、设计理念：“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。

教学应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。

学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者。

立体图形的性质与判定引言立体图形是我们日常生活中常见的物体，它们具有不同的形状和性质。

通过研究立体图形的性质和判定方法，我们可以更好地理解和应用这些图形。

一、立体图形的定义立体图形是具有三个维度的物体，包括长度、宽度和高度。

与平面图形相比，立体图形具有更多的信息和特征。

常见的立体图形包括立方体、圆柱体、圆锥体、球体等。

二、立体图形的性质1. 立体图形的表面积立体图形的表面积是指该图形所有表面的总面积。

不同的立体图形计算表面积的方法各不相同。

例如，立方体的表面积等于六个面的面积之和，而圆柱体的表面积等于两个底面的面积加上侧面的面积。

2. 立体图形的体积立体图形的体积是指该图形所占据的空间大小。

体积可以用来衡量物体的容量或大小。

计算立体图形的体积也有不同的方法。

例如，立方体的体积等于边长的立方，圆柱体的体积等于底面积乘以高度。

3. 立体图形的对称性立体图形可以具有不同的对称性，包括平面对称、旋转对称和反射对称。

平面对称是指图形可以通过某个平面进行对称，两边完全相同。

旋转对称是指图形可以通过某个中心点进行旋转，旋转后与原来的图形完全相同。

反射对称是指图形可以通过某个轴线进行对称，两边完全相同。

对称性可以帮助我们更好地理解和描述立体图形的形状。

4. 立体图形的角度立体图形中的角度也具有一定的性质。

例如，立方体的每个顶点都是四个面的交点，每个顶点的角度都是90度。

圆柱体的顶点角度为180度，而球体的每个点的角度为360度。

三、立体图形的判定方法1. 判定立体图形的种类通过观察立体图形的形状和特征，我们可以判定它属于哪一种立体图形。

例如，如果一个图形有六个面，每个面都是正方形，那么它就是一个立方体。

如果一个图形有一个平面底面和一个尖顶，那么它就是一个圆锥体。

2. 判定立体图形的性质除了判定立体图形的种类，我们还可以通过一些方法判定它的性质。

例如，通过测量立体图形的边长、面积和体积，我们可以了解它的大小和容量。