立体图形的表面积和体积

《立体图形的表面积和体积》评课稿
本节课的主要教学目标是让学生通过系统的整理、复习，进一步分清表面积和体积两个概念的不同含义，进一步理解、掌握立体图形的表面积和体积的意义及计算方法，加深对所学形体之间内在联系的认识。

我觉得田老师的这堂课设计的比较的好，主要体现在一下方面：
1、复习的层次分明，条理清晰。

在教学中，让学生在互相交流中复习了立体图形的表面积和体积，整理出来四种立体图形的表面积和体积的计算公式及其联系，回忆其推导过程，让学生进一步体会了转化、类比的思想，并能灵活的利用知识解决生活中的具体问题。

2、注重创设生活情境，体现数学与生活的密切联系。

本课的导入创设了“端午节包装礼物”的情景，多份礼物携带不方便，想自己制作长方体大纸箱，那么要知道什么为切入点，引导学生回忆起长方体的表面积和体积的知识，从而引出课题。

练习中最后一道习题与之呼应，让学生体会到数学来源于生活，学了数学知识又应该应用于生活。

3、注重学生自主整理，把知识进行整合、联系。

田老师让学生先独立完成表格四个立体图形的表面积和体积的填写，然后让他们选择其中的几个说说公式的推导过程，最后用一个练习来巩固。

这个练习是计算立体图形的表面积和体积，而这个立体图形是由长方体变成正方体，再变成圆柱，最后变成圆锥。

这样的一个练习，让学生更加深刻地理解他们之间的联系。

4、练习的形式和展示多种多样，有独立完成的，有只列式不计算的，有口头反馈的，有学生板演的，有投影展示的。

增加了练习时候的效果。

我觉得在复习课的趣味性上可以做一些功课，另外课堂上对学生的表扬可以更加的丰富。

总之，我觉得能听这样的一节复习课，受益匪浅！。

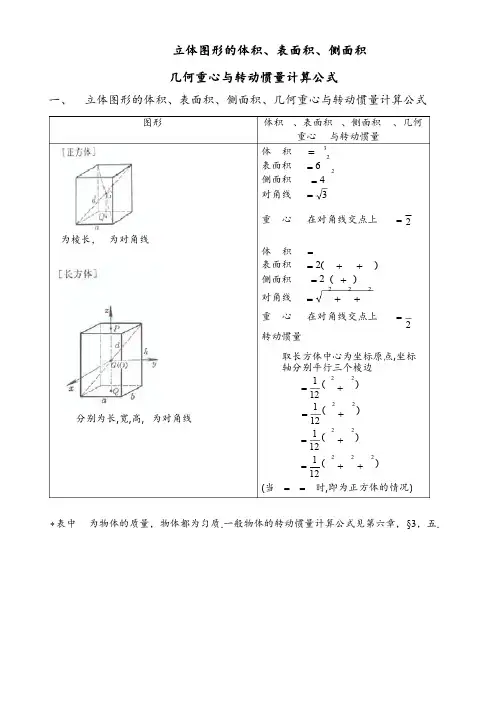
立体图形的体积、表面积、侧面积几何重心与转动惯量计算公式一、 立体图形的体积、表面积、侧面积、几何重心与转动惯量计算公式图形 体积、表面积、侧面积、几何重心与转动惯量为棱长，为对角线分别为长,宽,高,为对角线体 积 3=表面积26=侧面积24=对角线 3=重 心 在对角线交点上2=体 积 =表面积 )(2++=侧面积 )(2+=对角线222++=重 心 在对角线交点上2= 转动惯量取长方体中心为坐标原点,坐标轴分别平行三个棱边)(12122+=)(12122+=)(12122+=)(121222++= (当==时,即为正方体的情况)*表中为物体的质量，物体都为匀质.一般物体的转动惯量计算公式见第六章，§3，五.图形 体积、表面积、侧面积、几何重心与转动惯量为边长,为高为底边长,为高,为对角线为棱数,为底边长,为高,为斜高 体 积 =表面积 +=2侧面积 )(++=式中为底面积重 心2=(、分别为上下底重心)转动惯量对于正三棱柱()取为坐标原点,轴与棱平行1248324==体 积 225981.2233»=表面积61962.563322+»+= 侧面积 6=对角线224+=重 心2=(、分别为上下底重心)转动惯量取为坐标原点,轴与棱平行12583524==体 积 31=表面积 +=侧面积2'==式中为底面积,'为一侧三角形面重 心4h GQ = (Q 为底面的重心)图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量Ja,b,c,p,q,r 为棱长h 为高体积 011111010101028812222222222222c b ac p qb p r a q r V = 重心PQ GQ 41= (P 为顶点,Q 为底面的重心)体积)''(3FF F F h V ++=式中F F ,'分别为上下底面积重心 '''3'24FF F F F FF F PQ GQ ++++=(P ,Q 分别为上下底重心)分别为上下底边长,为棱数,为高,为斜高体 积÷÷øöççèæ÷øöçèæ++=2''13表面积 ++='侧面积 )'(2+=式中,'分别为上下底面积重 心2222'''3'24++++= (、分别为上下底重心)图形 体积、表面积、侧面积、几何重心与转动惯量两底为矩形,分别为上下底边长,为高,1为截头棱长体积]'')')('([6++++= '''1--=重心''2''2''3''2++++++= (分别为上下底重心)底为矩形,a,b为其边长,h为高,a’为上棱长r为半径 重心'2'2aaaaPQGQ++=(P为上棱中点,Q为下底面重心)体 积33352360.0634ddrV»==pp 表面积24rS p=重 心 G与球心O重合转动惯量取球心O为坐标原点mrJJJzyx252===mrJo253=图形 体积V、表面积S、侧面积M、几何重心G与转动惯量J[半球体]r为半径,O为球心r为球半径,a为弓形底圆半径,h为拱高,a为锥角(弧度)r为球半径,a为拱底圆半径,h为拱高 体 积 331232drVpp==表面积23rS p=侧面积22rM p=重 心 rGO83=转动惯量取球心O为坐标原点,z轴与GO重合 mrJJJzyx252===mrJo253=体 积 hrhrV220944.232»=p表面积 )2(ahrS+=p侧面积 (锥面部分) rM pa=重 心 )2(83hrGO-=转动惯量z轴与GO重合úûùêëé-÷øöçèæ-=2sin2cos2cos1215225aaap rJz÷øöçèæ+-=2cos2cos32533aahmr体 积)3(3)3(6222hrhhahV-=+=pp表面积 )2()2(222aharhS+=+=pp 侧面积(球面部分))(222harhM+==pp重 心)3()2(432hrhrGO--=图形 体积V、表面积S、侧面积M、几何重心G与转动惯量J[球台]r为球半径,a¢,a分别为上下底圆的半径,h为高R为中心半径,D为中心直径,r为圆截面半径,d为圆截面直径体 积 )'33(6222haahV++=p表面积 )'2(22aarhS++=p侧面积 rhM p2=2222222'÷÷øöççèæ--+=hhaaar重 心22244'33'23haaaahGO++-=222222'33'422haahaahGQ++++=(Q为下底圆心)体 积 222242DdRrVpp==表面积 DdRrS224pp==重 心 G在圆环的中心上转动惯量取圆环的中心为坐标原点,z轴垂直于圆环所在平面mRrJJyx÷÷øöççèæ+==28522mRrJz÷øöçèæ+=2243图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量J [圆柱体]r 为底面半径,h 为高R 为外半径,r 为内半径,h 为高r 为底圆半径,h,H 分别为最小,最大高度,a 为截角,D 为截头椭圆轴体 积h r V 2p = 表面积)(2h r r S +=p 侧面积rh M p 2= 重 心 2hGQ =(P ,Q 分别为上下底圆心) 转动惯量 取重心G 为坐标原点,z 轴垂直底面m h r J J y x ÷øöçèæ+==34122m r J z 22=体 积th R r R h V p p 2)(22=-= 表面积 )(222r R M S -+=p侧面积 R h r R h M p p 4)(2=+= 式中t 为管壁厚,R 为平均半径重 心2h GQ = 转动惯量 取z 轴与GQ 重合 m r R J z 2)(22+=体 积 )(22h H r V +=p 表面积 ÷øöçèæ++=a p cos 112r M S ÷øöçèæ+++=2D h H r r p 侧面积 )(h H r M +=p 截头椭圆轴22)(4h H r D -+= 重 心tan 22r h H +a)(2tan 2h H r GK +=a (GQ 为重心到底面距离,GK 为重心到轴线O O ¢的距离)图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量Jh 为截段最大高度,b 为底面拱高,2a 为底面弦长,r 为底面半径,a 2为弧所对圆心角(弧度)体 积])(3)3([3222a r b r a r a bh V -+-=÷øöçèæ--=a a a cos sin 31sin 33a b hr侧面积(柱面部分)])[(2a r b b rhM +-=a体 积abc abc V 1888.434»=p 重 心G 在椭球中心O 上 转动惯量 取椭球中心为坐标原点,z 轴与c 轴重合m c b J x )(5122+=m a c J y)(5122+= m b a J z)(122+=a,b,c 为半轴图形体积V 、表面积S 、侧面积M 、几何重心G 与转动惯量J体 积h r V 23p= 表面积 )(l r r S +=p 侧面积 rl M p = 母 线 22h r l +=重 心4h GQ = (Q 为底圆中心,O 为圆锥顶r为底圆半径,h为高,l为母线r,R分别为上,下底圆半径,h为高,l为母线上下底平行,F¢,F分别为上,下底面积,F为中截面面积,h为高取圆锥顶点为坐标原点,z轴与GQ 重合mhrJJyx÷÷øöççèæ+==22453mrJz2103=体 积 )(322RrrRhV++=p表面积 )(22rRMS++=p侧面积 )(rRlM+=p母 线22)(hrRl+-=圆锥高(母线交点到底圆的距离)rRhrhH-+=重 心2222324rRrRrRrRhGQ++++=(P,Q分别为上下底圆心)体 积 )4'(60FFFhV++»[注] 棱台、圆台、球台、圆锥、棱柱、圆柱等都是拟棱台的特例图形 体积V、表面积S、侧面积M、几何重心G与转动惯量Jd 为上,下底圆直径,D 为中截面直径,h 为高母线为圆弧时: 体积)2(26180.0)2(122222d D h d D hhV +»+=p2)2(08727.0d D h +»母线为抛物线时: 体积 ÷øöçèæ++=2243215d Dd D h V p )348(05236.022d Dd D h ++» 重心2h GQ = (P ,Q 分别为上下底圆心)二、 多面体[正四面体] [正八面体] [正十二面体] [正二十面体]图形面数f4 8 12 20 棱数k 6 12 30 30 顶点数e 462012体积V 31179.0a34714.0a36631.7a31817.2a表面积S27321.1a24641.3a26457.20a26603.8a表中a 为棱长.[欧拉公式] 一个多面体的面数为f ，棱数为k ，顶点数为e ,它们之间满足 2=+-f k e。

教育学科教师辅导讲义学员编号： 年 级： 课 时 数： 学员姓名： 辅导科目： 学科教师： 授课 类型T (立体图形相关知识点) C （典型例题试题讲解） T （拓展提高）授课日期时段教学内容知识点一：表面积1、长方体表面积=长x 宽× 2+ 宽× 高× 2+ 长×高× 2 字母公式：S=ax b× 2+ a× c× 2+ b×c× 2 或者：长方体的表面积 =( 长×宽 + 长×高 + 宽×高 ) × 2 。

字母公式：S=(ax b+ a× c+ b×c)× 22、正方体的表面积 =棱长×棱长×6。

字母公式：S=a ×a× 63、圆柱体的表面积：圆柱表面积=上底+下底+侧面（侧面面积=底面圆的周长×圆柱的高） 用字母表示：22s r ch π=+注：侧面积的求法：已知底面半径和高，rh π侧2s = 已知底面直径和高，dh π侧=s知识点二：体积1、长方体体积：长方体体积= ① 长×宽×高 （Ｖ＝ａｂｈ）② 底面积×高=横截面积×长 （V =sh ） 2、正方体的体积：正方体体积＝棱长×棱长×棱长检测题1：把一个圆柱的侧面展开，得到一个正方形．已知这个圆柱的高是10厘米，它的侧面积是（ ）平方厘米．A ．50B ．100C ．50πD ．100π答案：B检测题2．把一个棱长4厘米的正方体分割成两个长方体，表面积增加了______平方厘米．答案：64检测题3 一个正方体的棱长之和是48厘米，它的棱长是______厘米，表面积是______平方厘米，体积是______立方厘米． 答案：2 24 8检测题4 把两个棱长5厘米的正方体拼成一个长方体，这个长方体的表面积是______平方厘米．答案：250检测题5．一个练功房铺设了1600块长50厘米，宽10厘米，厚3厘米的木地板，这个练功房的面积有______平方米．答案：这个练功房的面积有80平方米．检测题6．圆柱的底面半径扩大2倍，高缩小到原来的21，它的体积就（ ）答案：扩大2倍检测题7．做一个圆柱体，侧面积是9.42平方厘米，高是3厘米，它的底面半径是______．答案：1.57cm一、专题精讲例1.如图是高为10厘米的圆柱，如果它的高增加4 厘米，那么它表面积就增加125.6平方厘米。

《立体图形的表面积与体积总复习》听课评课今天听了我校李老师的一节《立体图形的表面积与体积》总复习课。

通过本课的学习进一步巩固立体图形的相关知识，让学生的知识形成系统，训练学生的思维能力。

要紧的体会有以下几个方面：优点：1、条理清晰。

本节课围绕那个思想和环节设计，在教学中让学生在互相交流中复习了立体图形的表面积和体积，整理出来四种立体图形的表面积和体积的运算公式及其联系，回忆其推导过程，让学生进一步体会了转化、类比的思想，并能灵活的利用知识解决生活中的具体问题。

2、提高能力。

本节课，加强了指导，使学生在梳理里不至于无从着手。

课前让他们整理立体图形的知识，让学生自主选择整理的标准和方法，显现按立体图形的种类和按体积公式推导过程等不同方法来整理立体图形的知识。

凸现整理建构时学生的自主性，还学生一个自主整理的空间，让学生亲自去理一理知识，让学生在“做”中形成良好的认知结构，在“做”中学会整理建构的方法，获得整理建构的能力。

3、表达主体。

课堂上注重要学生多想多说，主动参与到学习活动中去。

如复习推导过程，让学生先闭上眼睛在头脑里回忆，再选择自己喜爱的图形说说，最后请学生观看老师的课件演示再次加快。

如此花时不多，却加深了学生对公式推导的印象，把握得较牢固。

不足：要练说，得练看。

看与说是统一的，看不准就难以说得好。

练看，确实是训练幼儿的观看能力，扩大幼儿的认知范畴，让幼儿在观看事物、观看生活、观看自然的活动中，积存词汇、明白得词义、进展语言。

在运用观看法组织活动时，我着眼观看于观看对象的选择，着力于观看过程的指导，着重于幼儿观看能力和语言表达能力的提高。

1、要加强分析和明白得。

差不多的运算公式和运算学生差不多把握，然而在解决实际问题的时候容易将表面积公式与体积公式混淆。

课本、报刊杂志中的成语、名言警句等俯首皆是,但学生写作文运用到文章中的甚少,即使运用也专门难做到恰如其分。

什么缘故?依旧没有完全“记死”的缘故。

立体图形的表面积与体积立体图形是我们常见的一种几何图形，它具有三个维度：长度、宽度和高度。

对于一个立体图形来说，其表面积和体积是两个重要的参数。

本文将详细介绍立体图形的表面积与体积的计算方法及其应用。

一、立体图形的表面积计算方法立体图形的表面积是指该图形所有面积之和。

不同类型的立体图形，其表面积计算公式也不同。

下面我们将逐一介绍几种常见立体图形的表面积计算方法。

1. 立方体的表面积计算公式立方体是最简单的一种立体图形，其所有面都是正方形。

设立方体的边长为a，则立方体的表面积S为S = 6a^2。

2. 正方体的表面积计算公式正方体的所有面同样是正方形。

设正方体的边长为a，则正方体的表面积S等于立方体的表面积，即S = 6a^2。

3. 圆柱体的表面积计算公式圆柱体包括一个底面和一个侧面。

设底面的半径为r，圆柱体的高度为h，则圆柱体的表面积S = 2πrh + πr^2。

4. 圆锥体的表面积计算公式圆锥体包括一个底面和一个侧面。

设底面的半径为r，圆锥体的高度为h，则圆锥体的表面积S = πrl + πr^2，其中l为圆锥体的斜高。

5. 球体的表面积计算公式球体是一种特殊的立体图形，其表面由无数个点组成。

设球体的半径为r，则球体的表面积S = 4πr^2。

二、立体图形的体积计算方法立体图形的体积是指该图形所包围的三维空间的大小。

与表面积一样，不同类型的立体图形的体积计算公式也各不相同。

下面我们将介绍几种常见立体图形的体积计算方法。

1. 立方体的体积计算公式立方体的体积计算最简单，其体积V等于边长的立方，即V = a^3。

2. 正方体的体积计算公式正方体的体积与立方体相同，即V = a^3。

3. 圆柱体的体积计算公式圆柱体的体积V等于底面积乘以高度，即V = πr^2h。

4. 圆锥体的体积计算公式圆锥体的体积V等于底面积乘以高度再除以3，即V = (1/3)πr^2h。

5. 球体的体积计算公式球体的体积V等于4/3乘以π乘以半径的立方，即V = (4/3)πr^3。

面积体积表面积公式大全一、平面图形面积公式。

1. 长方形。

- 面积公式：S = ab（其中a为长，b为宽）。

2. 正方形。

- 面积公式：S=a^2（其中a为边长）。

3. 三角形。

- 面积公式：S=(1)/(2)ah（其中a为底边长，h为这条底边对应的高）。

- 已知三角形三边a、b、c，还可以用海伦公式S = √(p(p - a)(p - b)(p - c))，其中p=(a + b+ c)/(2)。

4. 平行四边形。

- 面积公式：S = ah（其中a为底边长，h为这条底边对应的高）。

5. 梯形。

- 面积公式：S=((a + b)h)/(2)（其中a、b为梯形的上底和下底，h为梯形的高）。

6. 圆。

- 面积公式：S=π r^2（其中r为圆的半径）。

- 扇形面积公式：S=frac{nπ r^2}{360}（其中n为扇形圆心角的度数，r为扇形所在圆的半径）。

二、立体图形体积公式。

1. 长方体。

- 体积公式：V=abc（其中a、b、c分别为长方体的长、宽、高）。

2. 正方体。

- 体积公式：V = a^3（其中a为正方体的边长）。

3. 圆柱。

- 体积公式：V=π r^2h（其中r为圆柱底面半径，h为圆柱的高）。

4. 圆锥。

- 体积公式：V=(1)/(3)π r^2h（其中r为圆锥底面半径，h为圆锥的高）。

5. 球。

- 体积公式：V=(4)/(3)π r^3（其中r为球的半径）。

三、立体图形表面积公式。

1. 长方体。

- 表面积公式：S = 2(ab+bc + ac)（其中a、b、c分别为长方体的长、宽、高）。

2. 正方体。

- 表面积公式：S = 6a^2（其中a为正方体的边长）。

3. 圆柱。

- 表面积公式：S = 2π r^2+2π rh（其中r为圆柱底面半径，h为圆柱的高）。

4. 圆锥。

- 侧面积公式：S_侧=π rl（其中r为圆锥底面半径，l为圆锥的母线长）。

- 表面积公式：S=π r^2+π rl。

5. 球。

优秀课例评析设计理念：本课是冀教版六年级下册“回顾整理”版块内容，教师通过让学生自己整理公式、回忆推导过程、课堂交流疑难点、运用公式练习等教学环节，系统复习小学数学中学过的立体图形的表面积和体积公式，梳理沟通各种图形之间内在的关系。

通过复习，使学生进一步认识表面积和体积的概念，理解和掌握表面积和体积的计算方法，培养学生应用有关知识解决实际问题的能力。

六年级学生有了一定的知识基础和生活经验，抽象逻辑思维能力也获得了一定的发展，初步具备了主动学习和自学的能力，能根据具体要求有序地展开思考、讨论，合作交流，获得丰富的知识再现，在老师的引导下，相信他们有能力去将尚不清晰的相关知识加以整理，内化整合，形成体系。

教学目标：1.经历总结、整理立体图形的表面积和体积公式的过程。

2.进一步理解和掌握表面积和体积的计算公式，培养对知识进行归纳、整理的学习能力，进一步体会转化的数学思想。

3.在学生利用公式计算的过程中，解决学生易错的问题。

教学重点：学习归纳、整理的学习方法，灵活运用立体图形的表面积和体积的计算方法解决实际问题。

教学难点：体会转化的数学思想，沟通体积计算方法之间的联系。

课前准备：课前布置整理要求，学生自己整理表面积和体积公式及推导过程。

整理提示：对我们学过的立体图形的相关知识进行整理，注意以下几点：1.写出学过的立体图形的表面积和体积公式。

2.整理过程中认真回忆它们的体积公式是怎样推导出来的（可以说一说，也可写一写或画一画），并想想它们之间的联系。

3.整理结果要简洁明了，条理清晰，层次“立体图形的表面积和体积”教学实录王春红（石家庄市北新街小学，河北石家庄050003）关键词：小学数学；立体图形的表面积和体积；教学实录中图分类号：G623.5文献标识码：B文章编号：1009-010X（2016）20-0075-06. All Rights Reserved.分明。

教学实录一、开门见山，直接导入师谈话揭题：（课件出示整理提示）昨天我们布置了一项作业，按这份整理要求对立体图形的表面积和体积公式进行了整理，这节课我们就在大家整理的基础上对这部分知识进行再次的梳理（板书课题：表面积和体积）。

五年级几何体的表面积与体积的计算(可以直接使用，可编辑实用优秀文档，欢迎下载）空间与图形教师辅导讲义——立体图形的知识与应用知识要点长方体、正方体、圆柱体、圆锥体的表面积及体积1．表面积：物体表面面积的总和，叫做物体的表面积。

表面积通常用S 表示。

常用面积单位是平方千米、平方米、平方分米、平方厘米。

2．体积：物体所占空间的大小，叫做物体的体积。

体积通常用V 表示。

常用体积单位是立方米、立方分米、立方厘米。

3．容积：箱子、油桶、仓库等所能容纳物体的体积，叫做它们的容积或容量。

常用容积单位是升、毫升。

4．体积与容积单位之间的换算：1立方分米=l 升，1立方厘米=l 毫升。

5．体积和容积的异同点 容积的计算方法跟体积的计算方法相同，但要从容器的里面量长、宽、高，而计算体积要从物体的外面量长、宽、高。

计量体积用体积单位，计量容积除了用体积单位外，还可以用容积单位升和毫升。

6. 立体图形的表面积、侧面积和体积计算公式相同点不同点 面棱顶点面的特点 面的大小 棱长 长方体6个12条8个6个面一般都是长方形，也可能有两个相对的面是正方形相对的面的面积相等每一组互相平行的四条棱的长度相等正方体6个12条8个6个面都是相等的正方形6个面的面积都相等12条棱长的长度都相等精典题型分析1、一个零件形状大小如下图：算一算，它的体积是多少立方厘米，表面积是多少平方厘米。

（单位：厘米）练习：学校生物小组做了一个昆虫箱（如图）。

昆虫箱的上、下、左、右面是木板，前、后面装纱网。

①制作这样一个昆虫箱，至少需要多少平方厘米的木板？②制作这样一个昆虫箱，至少需要多少平方厘米的纱网？2、在一个长15分米，宽12分米的长方体水箱中，有10分米深的水。

如果在水中沉入一个棱长为30厘米的正方体铁块，那么，水箱中水深多少分米？练习1：一个长方体的玻璃缸内有一些水，水面距离上沿0.6分米（如图）。

准备在缸内放入一块体积是60立方分米的假山石（假山石能全部浸在水中），水会溢出吗？如果会溢出，溢出多少立方分米？练习2：一个正方体玻璃容器，从里面量棱长是2dm。

小学立体图形知识点在小学阶段，数学的学习中会涉及到各种各样的立体图形，这是培养孩子们空间想象力和逻辑思维能力的重要部分。

接下来，让我们一起走进小学立体图形的世界，来了解一下相关的重要知识点。

首先，我们来认识一下常见的立体图形有哪些。

最基础的莫过于长方体、正方体、圆柱体和圆锥体了。

长方体是由六个长方形（特殊情况下有两个相对的面是正方形）围成的立体图形。

它有 8 个顶点，12 条棱，相对的棱长度相等。

长方体还有 6 个面，相对的面完全相同。

计算长方体的表面积时，我们可以用公式：长方体表面积＝（长×宽＋长×高＋宽×高）× 2 。

而长方体的体积＝长×宽×高。

正方体则是特殊的长方体，它的六个面都是完全相同的正方形，12 条棱长度都相等。

正方体的表面积＝棱长×棱长× 6 ，体积＝棱长×棱长×棱长。

圆柱体是由两个底面和一个侧面组成的。

两个底面是完全相同的圆，侧面展开是一个长方形。

圆柱体的表面积包括两个底面的面积和侧面的面积，即圆柱体表面积＝底面积× 2 ＋侧面积，侧面积＝底面周长×高，底面积＝圆周率×半径×半径。

圆柱体的体积＝底面积×高。

圆锥体是由一个底面和一个侧面组成的，底面是一个圆，侧面展开是一个扇形。

圆锥体的体积＝ 1/3×底面积×高。

在学习立体图形的过程中，孩子们需要掌握如何观察和描述这些图形的特征。

比如，看到一个长方体，能够说出它的面、棱、顶点的数量和特点；看到一个圆柱体，能够指出它的底面、侧面以及高的位置。

同时，还需要学会测量和计算立体图形的相关数据。

比如，要知道如何测量长方体的长、宽、高，如何通过测量数据计算出它的表面积和体积。

立体图形之间也存在着一些关系。

比如，当把一个圆柱体沿着直径切成两个半圆柱体时，增加的表面积就是两个长方形的面积，长方形的长就是圆柱的高，宽就是圆柱的底面直径。