第三章振动与冲击理论基础37页PPT
- 格式:ppt
- 大小:3.15 MB
- 文档页数:37

振动与冲击振动与冲击是物理学中的两个重要概念,它们在我们的日常生活中无处不在,影响着我们周围的一切。
从最简单的机械振动到地震的冲击波,振动与冲击的研究既有理论性的探索,也有实践性的应用。
振动是物体围绕平衡位置做周期性的来回运动。
这种运动可以是机械振动,也可以是电磁振动。
机械振动包括弹簧振子、摆动、杆振动等,而电磁振动则包括光波的传播和电子在电路中的运动等。
无论是什么形式的振动,都遵循着特定的物理规律,如简谐振动和受迫振动等。
简谐振动是最简单的一种振动形式,它的运动规律可以用正弦函数来描述。
简谐振动具有固有频率和周期,当外力作用于振动体时,振动的频率和振幅都会发生改变。
而受迫振动则是在外力作用下,振动体受到迫使而做非简谐振动。
受迫振动有着复杂的动态行为,其中包括共振现象。
冲击是一种短暂的、非周期性的作用力。
它具有较大的力量和较短的作用时间,从而使被作用物体发生瞬时的突变。
常见的冲击包括物体撞击、爆炸和地震等。
发生冲击时,物体会受到巨大的变形和力量的作用,有时会导致破坏性的后果。
振动与冲击不仅仅是物理学的领域,它们也在许多其他学科中有着广泛的应用。
在工程领域中,我们可以利用振动和冲击现象来设计和改进机械结构,提高其性能和稳定性。
在建筑工程中,地震波的冲击力对建筑物的稳定性有着重大影响,需要进行合理的结构设计和抗震措施。
在交通运输领域,汽车和飞机的振动和冲击对乘坐舒适度和安全性都有着显著影响,需要通过设计和改进减震系统来达到良好的效果。
此外,振动与冲击的研究还可以应用于医疗领域。
例如,医学中的超声波成像技术就是利用声波的振动特性来观察人体内部的结构和疾病情况。
此外,推拿按摩等疗法也是利用振动和冲击来促进血液循环和缓解肌肉疼痛。
总之,振动与冲击是自然界中普遍存在的现象,对我们的生活和工作都具有重要意义。
通过对振动与冲击的深入研究和应用,我们可以更好地理解和掌握自然界的规律,并将其用于改善人类的生活条件和推动科技进步。


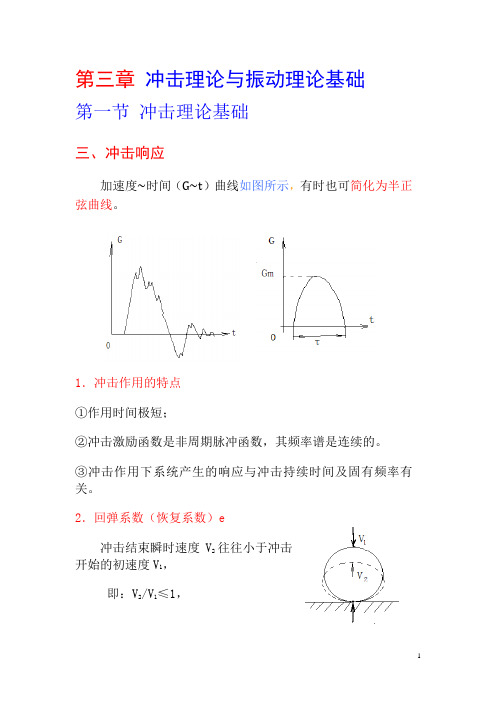
第三章冲击理论与振动理论基础第一节冲击理论基础三、冲击响应加速度~时间(G~t)曲线如图所示,有时也可简化为半正弦曲线。
1.冲击作用的特点①作用时间极短;②冲击激励函数是非周期脉冲函数,其频率谱是连续的。
③冲击作用下系统产生的响应与冲击持续时间及固有频率有关。
2.回弹系数(恢复系数)e冲击结束瞬时速度V2往往小于冲击开始的初速度V1,即:V2/V1≤1,令e=|12V V | 则有:O ≤e ≤1 e 表明了物体变形或回弹的程度,可通过实验测定。
H 1——跌落高度,H 2——回弹高度于是:1212H H V V e ==根据e 值的大小,冲击可分为弹性冲击(o <e <1)、完全弹性冲击(e=1)、非弹性(塑性)冲击(e=0)。
3.速度增量△V()gHe V e V V V 2)11121+=+=+=(△ 因为 0<e<1, 所以gH V gH 222≤≤△ 机械冲击时速度增量可写成:adt dv v v V o ⎰⎰==τ21△即速度增量在数值上等于冲击脉冲下的面积。
4.冲击放大系数A m设G c 为易损部件所经受的最大冲击加速度,G m 为产品因受冲击而产生的最大加速度,τ为冲击持续时间。
放大系数:产品的易损部件的冲击加速度(响应)与产品m 2产生的冲击加速度(激励)的比值,即:A m =m c G G∴G c =A m ·G m 由21f f =λ值查找对应的Am 值。
⑤举例例1.有一脆弱元件的固有频率为38Hz 的包装件受到一次半正弦脉冲冲击(激励)。
已知该脉冲的峰值加速度G m 为100(g ′s),冲击持续时间τ=25ms ,试问该冲击对脆弱元件产生什么样的作用?若脆弱元件的脆值(安全加速度值)G s =160(g 's ),试估计产品是否安全。
解:1°由已知条件知,f 1=38Hz ,τ=25ms 。
等效冲击振动频率f 2=τ2112=T Hz 20025.021=*= 2°由21f f 90.12038==, 查表可知:A m =1.7473°G c =A m ·G m =1.747×100=174.14°∵G s =160<G c =174.7∴不能保护产品。


振动与冲击1. 引言振动与冲击是物理学中一个重要的研究领域,涉及到许多物理现象和工程应用。
振动指的是物体或系统在一定时间范围内往复运动的现象,而冲击则是突然产生的、短暂而强烈的外力作用于物体的现象。
振动和冲击都是自然界和生活中经常遇到的现象,深入研究和理解振动与冲击对于工程设计、结构优化和故障分析等方面有重要的意义。
2. 振动的基本概念和特性振动是物体或系统在时间上的往复运动。
振动的基本特性包括频率、振幅和周期。
频率是指在单位时间内振动的次数,单位为赫兹(Hz)。
振幅是指振动过程中物体或系统离开平衡位置的最大位移,通常用米(m)来表示。
周期是指物体或系统完成一个完整振动循环所需要的时间,单位为秒(s)。
振动的类型可以分为自由振动和强迫振动。
自由振动是指物体或系统在无外力作用下的振动,其频率由物体的固有特性决定。
而强迫振动是指物体或系统在受到外力作用下的振动,其频率和外力的特性有关。
3. 振动的应用振动在各个领域和行业都有着广泛的应用。
以下是一些典型的振动应用案例:3.1 振动传感器振动传感器是一种能够测量和监测物体振动的设备。
它广泛应用于机械设备、航空航天、汽车工业等领域。
振动传感器可以帮助监测机械设备的运行状况,及时发现故障和异常振动,以保证设备的正常运行和安全性。
3.2 振动控制振动控制是通过采用各种技术手段来减小或消除振动对系统和结构的影响。
例如,通过安装阻尼器或减振器来减小机械设备产生的振动;通过调整车辆的悬挂系统来降低行驶时的振动。
3.3 振动测试与分析振动测试与分析是通过测量物体或系统的振动响应,来了解其结构、性能和健康状况的一种方法。
通过振动测试和分析,可以识别出结构的固有频率、模态分布和故障状态,从而为工程优化和故障诊断提供依据。
4. 冲击的基本概念和特性冲击是指突然产生的、短暂而强烈的外力作用于物体的现象。
冲击的特性包括幅度、持续时间和冲击力。
幅度是指冲击产生的位移或形变,通常用米(m)来表示。