2011年高考数学模拟试题_理科_

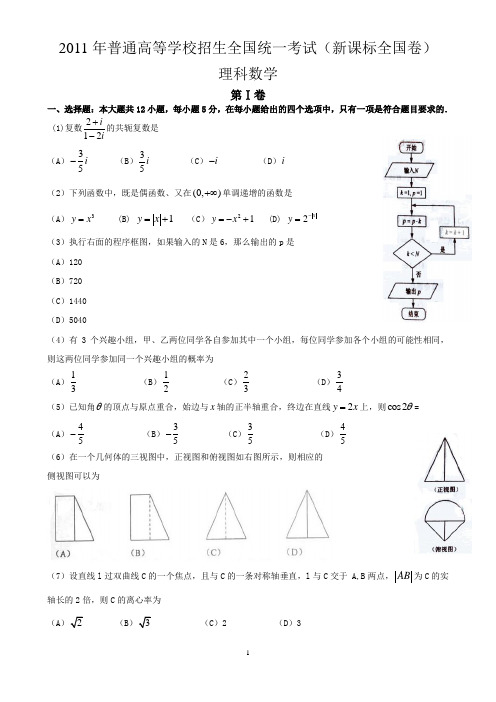
2011年普通高等学校招生全国统一考试（新课标全国卷）理科数学第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． (1)复数212ii+-的共轭复数是（A ）35i - （B ）35i （C ）i - （D ）i （2）下列函数中，既是偶函数、又在(0,)+∞单调递增的函数是 （A ）3y x = (B) 1y x =+ （C ）21y x =-+ (D) 2xy -=（3）执行右面的程序框图，如果输入的N 是6，那么输出的p 是 （A ）120 （B ）720 （C ）1440 （D ）5040（4）有3个兴趣小组，甲、乙两位同学各自参加其中一个小组，每位同学参加各个小组的可能性相同，则这两位同学参加同一个兴趣小组的概率为 （A ）13 （B ）12 （C ）23 （D ）34（5）已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ= （A ）45-（B ）35- （C ）35 （D ）45（6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的 侧视图可以为（7）设直线l 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，l 与C 交于 A,B 两点，AB 为C 的实轴长的2倍，则C 的离心率为（A ）2 （B ）3 （C ）2 （D ）3（8）512a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为2，则该展开式中常数项为（A ）-40 （B ）-20 （C ）20 （D ）40 （9）由曲线y x =，直线2y x =-及y 轴所围成的图形的面积为（A ）103 （B ）4 （C ）163（D ）6 （10）已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈⎥⎝⎦3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P （11）设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则（A ）()f x 在0,2π⎛⎫⎪⎝⎭单调递减 （B ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 （C ）()f x 在0,2π⎛⎫⎪⎝⎭单调递增（D ）()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 (12)函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有焦点的横坐标之和等于 （A ）2 (B) 4 (C) 6 (D)8第Ⅱ卷本卷包括必考题和选考题两部分．第(13)题～第(21)题为必考题，每个试题考生都必须做答．第(22)题～第(24)题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．（13）若变量,x y 满足约束条件329,69,x y x y ≤+≤⎧⎨≤-≤⎩则2z x y =+的最小值为 。

卢湾区2011年高考模拟考试数学试卷（理科） 2011.4（本卷完成时间为120分钟，满分为150分）一．填空题（本大题满分56分）本大题共有14小题，考生应在答题纸相应编号的空格内直接写结果，每个空格填对得4分，否则一律得零分．1.不等式|2|x -≤1的解集是 ．2.函数21x y =-的反函数为 ．3.方程2sin 2sin 0x x -=的解集为 ．4.若实数对(,)x y 满足224x y +=，则xy 的最大值为 ．5.若关于x , y 的线性方程组的增广矩阵为0603m n ⎛⎫ ⎪⎝⎭，该方程组的解为3,4.x y =-⎧⎨=⎩则mn 的值为 ．6.在极坐标系中，点A 的极坐标为(2,0) ，直线l 的 极坐标方程为(cos sin )20ρθθ++=，则点A 到直 线l 的距离为 ．7.某算法的流程图如图所示，则该算法输出的n 值 是 ． 8.已知251(2)nx x+(n ∈N *)的展开式中含有常数项，则n 的最小值是 ． 9．已知02πα<<,02πβ-<<,3cos()5αβ-=，且3tan 4α=，则sin β= ．10. 一长方形的四个顶点在直角坐标平面内的射影的坐标分别为(1,2),- (3,3), (3,5),-(1,6)，则此长方形的中心在此坐标平面内的射影的坐标是 ．11．某船在A 处看灯塔S 在北偏东30︒方向，它以每小时30海里的速度向正北方向航行，经过40分钟航行到B 处，看灯塔S 在北偏东75︒方向，则此时该船到灯塔S 的距离约为 海里（精确到0.01海里）．12.已知抛物线22(0)y px p =>，过定点(,0)p 作两条互相垂直的直线12, l l ，1l 与抛物线交于, P Q 两点，2l 与抛物线交于, M N 两点，设1l 的斜率为k ．若某同学已正确求得弦PQ 的中垂线在y 轴上的截距为32p p kk+，则弦MN 的中垂线在y 轴上的截距为．输出n 开始否n ←n +1 2n ＞n 2是结束n ←1 （第7题图）13．已知向量OA，OB的夹角为π3，||4OA = ，||1OB = ，若点M 在直线OB 上，则||OA OM -的最小值为 ． 14.已知集合2(21)cos ,n A x x n m-π⎧⎫==∈⎨⎬⎩⎭Z ，当m 为4022时，集合A 的元素个数为 ．二．选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分． 15．“πϕ=”是“函数()sin()f x x ϕ=+是奇函数”的 （ ）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分又非必要条件 16．已知数列{}n a 是无穷等比数列，其前n 项和是n S ，若232a a +=，341a a +=，则l i m n n S →∞的值为 （ ） A ．23B ．43C ．83D ．16317.已知复数z 满足z 12i z 2i 32---++=（i 是虚数单位），若在复平面内复数z 对应的点为Z ，则点Z 的轨迹为 （ ）A ．双曲线的一支B ．双曲线C ．一条射线D ．两条射线 18.已知234101()1234101xxxxf x x =+-+-+⋅⋅⋅+，234101()1234101xxxxg x x =-+-+-⋅⋅⋅-，若函数()f x 有唯一零点1x ，函数()g x 有唯一零点2x ，则有 （ ） A ．12(0,1),(1,2)x x ∈∈ B ．12(1,0),(1,2)x x ∈-∈ C ．12(0,1),(0,1)x x ∈∈ D ．12(1,0),(0,1)x x ∈-∈三．解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应的编号规定区域内写出必要的步骤． 19．（本题满分12分）已知矩形ABC D 内接于圆柱下底面的圆O ，PA 是圆柱的母线，若6AB =，8AD =，此圆柱的体积为300π，求异面直线A C 与PB 所成角的余弦值．APBCDO20．（本题满分13分）本题共有2个小题，第1小题满分5分，第2小题满分8分．某校10名学生组成该校“科技创新周”志愿服务队（简称“科服队”），他们参加活动的有关数据统计如下：（1）从“科服队”中任选3人，求这3人参加活动次数各不相同的概率；（2）从“科服队”中任选2人，用ξ表示这2人参加活动次数之差的绝对值，求随机变量ξ的分布列及数学期望E ξ．21．（本题满分13分）本题共有2个小题，第1小题满分6分，第2小题满分7分．已知椭圆E ：22221x y ab+=(0a b >>)过点(3, 1)P ，其左、右焦点分别为12, F F ，且126F P F P ⋅=-．（1）求椭圆E 的方程；（2）若,M N 是直线5x =上的两个动点，且12F M F N ⊥，则以M N 为直径的圆C 是否过定点？请说明理由．参加活动次数 1 2 3 人 数23522．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分9分．已知数列c b a ,,是各项均为正数的等差数列，公差为d （d >0）．在b a ,之间和b,c 之间共插入n 个实数，使得这3n +个数构成等比数列，其公比为q ． （1）求证：||1q >；（2）若1,1 a n ==，求d 的值；（3）若插入的n 个数中，有s 个位于a,b 之间，t 个位于b,c 之间，且,s t 都为奇数，试比较s 与t 的大小，并求插入的n 个数的乘积（用,,a c n 表示）.23．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分．对于定义域为D 的函数()y f x =，若有常数M ，使得对任意的1x D ∈，存在唯一的2x D ∈满足等式12()()2f x f x M +=，则称M 为函数y =f (x )的“均值”． （1）判断1是否为函数()21(1f x x =+-≤x ≤1)的“均值”，请说明理由；（2）若函数2()2(12,f x ax x x =-<<a 为常数）存在“均值”，求实数a 的取值范围； （3）若函数()f x 是单调函数，且其值域为区间I ．试探究函数()f x 的“均值”情况（是否存在、个数、大小等）与区间I 之间的关系，写出你的结论（不必证明）． 说明：对于（3），将根据结论的完整性与一般性程度给予不同的评分．卢湾区2011年高考模拟考试数学试题（理科）参考答案与评分标准一、选择题：（每小题4分）1. [1,3]2.2log (1)y x =+3. {|,}Ζx x k k =π∈4. 25. 24-6. 227. 5 8． 7 9．725-10．(0,4)11．14.14 12. 32pk pk -- 13．23 14.1006 二．选择题（每小题5分）15．A 16．D 17．C 18．B19．解：设圆柱下底面圆O 的半径为r ，连A C ， 由矩形ABC D 内接于圆O ，可知A C 是圆O 的直径， 于是2226810r A C ==+=，得5r =， ……………3分又圆柱的体积25300V PA =π⋅=π，可得12PA =．……6分 分别以直线,,A B A D A P 为,,x y z 轴，建立空间直角坐标系A xyz -，可得(6,8,0),(6,0,12)AC PB ==-，………8分 设异面直线A C 与PB 所成角所成的角θ，向量AC 与PB的夹角为ϕ，则||3635cos |cos |25||||1065AC PB AC PB θϕ⋅====⋅⨯ ， 故异面直线A C 与PB 所成角的余弦值为3525． ………………………………12分20．解：（1）3人参加活动次数各不相同的概率为111235310C C C 1C 4P ==故这3名同学中参加活动次数各不相同的概率为14． ……………………………5分（2）由题意知：ξ=0, 1, 2，222235210C C C 14(0)C 45P ξ++===； ……………7分11112335210C C C C 217(1)C 4515P ξ+====； ……………9分1125210C C 102(2)C 459P ξ====． ……………10分ξ的分布列为 ：x0 12APB CDOxyz……………11分所以ξ的数学期望:1472410124515945E ξ=⨯+⨯+⨯=． ………………………13分21．解：（1）设点12,F F 的坐标分别为(,0),(,0)(0)c c c ->，则12(3,1),(3,1),F P c F P c =+=-故212(3)(3)1106F P F P c c c ⋅=+-+=-=-，可得4c =， …………………2分所以2222122||||(34)1(34)162a PF PF =+=+++-+=，…………………4分 故22232,18162a b a c ==-=-=， 所以椭圆E 的方程为221182xy+=． ……………………………6分（2）设,M N 的坐标分别为(5,),(5,)m n ，则12(9,),(1,)F M m F N n ==，又12F M F N ⊥ ，可得1290F M F N m n ⋅=+=，即9m n =-， …………………8分又圆C 的圆心为(5,),2m n +半径为||2m n -，故圆C 的方程为222||(5)()()22m n m n x y +--+-=，即22(5)()0x y m n y mn -+-++=，也就是22(5)()90x y m n y -+-+-=， ……………………11分 令0y =，可得8x =或2，故圆C 必过定点(8,0)和(2,0)． ……………………13分 （另法：（1）中也可以直接将点P 坐标代入椭圆方程来进行求解；（2）中可利用圆C 直径的两端点直接写出圆C 的方程） 22．解：（1）由题意知2n c q a+=，2c a d =+，又0,0a d >>，可得2211n c d q a a+==+>， ………………………………2分即2||1n q +>，故2||1n q +>，又2n +是正数，故||1q >．………………………………4分 （2）由,,a b c 是首项为1、公差为d 的等差数列，故d c d b 21,1+=+=， 若插入的这一个数位于,a b 之间，则21q d =+，321q d =+， 消去q 可得32)1()21(d d +=+，即320d d d --=，其正根为251+=d ．………7分若插入的这一个数位于,b c 之间，则q d =+1，321q d =+，()P x ξ=144571529消去q 可得3)1(21d d +=+，即3230d d d ++=，此方程无正根． 故所求公差251+=d ． ………………………………………9分（3）由题意得1s b a d q aa++==，12t c a d q ba d ++==+，又0,0a d >>，故220()a d a d daa da a d ++-=>++，可得2a d a d aa d++>+，又20a d a d+>+，故110s t q q ++>>，即11||||s t q q ++>．又||1q >，故有11s t +>+，即s t >． ………………………………………12分 设3n +个数所构成的等比数列为}{n a ，则123,,2s n a c a a a b a c +++====，由413(2,3,4,k n k n a a a a ac k +-+===…，2)n +，可得32(a a (2)22231)()()n n n a a a a a +++= (1)1322()()()n n n a a a a ac +++=， ……………………14分又10s b q a+=>，01>=+bc qt ，由,s t 都为奇数，则q 既可为正数，也可为负数，①若q 为正数，则23a a …2n a +12()n ac +=，插入n 个数的乘积为122()n ac a c++；②若q 为负数，,,32a a …2,n a +中共有12n +个负数，故32a a (1)(1)222(1)()n n n a ac +++=-，所插入的数的乘积为2a c +1(1)22(1)()n n ac ++-．所以当42(n k k =-∈N*)时，所插入n 个数的积为122()n ac a c++；当4(n k k =∈N*）时，所插入n 个数的积为122()n ac a c+±+． …………………18分（另法：由又10s b q a+=>，01>=+bc qt ，20n c qa+=>由,s t 都为奇数，可知n 是偶数，q 既可为正数也可为负数．23a a …2n a +23()()()aq aq aq =…(1)(2)112()n n n n aqaq++++=①若q 为正数，则23a a …2n a +111121222()()()n n n n n n ca q aac a ++++++===，故插入n 个数的乘积为122()n ac a c++； …………………15分②若q 为负数，由n 是偶数，可知(1)(2)2n n ++的奇偶性与22n +的奇偶性相同，可得23a a …2n a +2122(1)()n n ac ++=-．所以当42(n k k =-∈N*)时，所插入n 个数的积为122()n ac a c++；当4(n k k =∈N*）时，所插入n 个数的积为122()n ac a c+±+． …………………18分）23．解：（1）对任意的1[1,1]x ∈-，有1[1,1]x -∈-， 当且仅当21x x =-时，有1212()()112f x f x x x +=++=，故存在唯一2[1,1]x ∈-，满足12()()12f x f x +=， ……………………2分所以1是函数()21(11)f x x x =+-≤≤的“均值”． ……………………4分 (另法：对任意的1[1,1]x ∈-，有1[1,1]x -∈-，令21x x =-， 则2[1,1]x ∈-，且1212()()112f x f x x x +=++=，若2[1,1]x '∈-，且12()()12f x f x '+=，则有22()()f x f x '=，可得22x x '=，故存在唯一2[1,1]x ∈-，满足12()()12f x f x +=， ……………………2分所以1是函数()21(11)f x x x =+-≤≤的“均值”． ……………………4分） （2）当0a =时，()2(12)f x x x =-<<存在“均值”，且“均值”为3-；…………5分 当0a ≠时，由2()2(12)f x ax x x =-<<存在均值，可知对任意的1x ， 都有唯一的2x 与之对应，从而有2()2(12)f x ax x x =-<<单调， 故有11a ≤或12a≥，解得1a ≥或0a <或102a <≤， ……………………9分综上，a 的取值范围是12a ≤或1a ≥． ……………………10分（另法：分0,a =1111,12,2a aa≤<<≥四种情形进行讨论）（3）①当I (,)a b =或[,]a b 时，函数()f x 存在唯一的“均值”． 这时函数()f x 的“均值”为2a b +； …………………12分②当I 为(,)-∞+∞时，函数()f x 存在无数多个“均值”．这时任意实数均为函数()f x 的“均值”； ……………………14分③当I (,)a =+∞或(,)a -∞或[,)a +∞或(,]a -∞或[,)a b 或(,]a b 时，函数()f x 不存在“均值”． ……………………16分 [评分说明：若三种情况讨论完整且正确，但未用等价形式进行叙述，至多得6分；若三种情况讨论不完整，且未用等价形式叙述，至多得5分]①当且仅当I 形如(,)a b 、[,]a b 其中之一时，函数()f x 存在唯一的“均值”． 这时函数()f x 的“均值”为2a b +； ……………………13分②当且仅当I 为(,)-∞+∞时，函数()f x 存在无数多个“均值”．这时任意实数均为函数()f x 的“均值”； ……………………16分③当且仅当I 形如(,)a +∞、(,)a -∞、[,)a +∞、(,]a -∞、[,)a b 、(,]a b 其中之一时，函数()f x 不存在“均值”． ……………………18分 （另法：①当且仅当I 为开区间或闭区间时，函数()f x 存在唯一的“均值”．这时函数()f x 的均值为区间I 两端点的算术平均数； ……………………13分②当且仅当I 为(,)-∞+∞时，函数()f x 存在无数多个“均值”．这时任意实数均为函数()f x 的“均值”； ……………………16分③当且仅当I 为除去开区间、闭区间与(,)-∞+∞之外的其它区间时，函数()f x 不存在“均值”． ……………………18分）[评分说明：在情形①与②中，等价关系叙述正确但未正确求出函数“均值”，各扣1分]。

(免费)2011年高考数学模拟试卷(1)附答案-打印版2011年高考数学模拟试卷（1）附答案（打印版）一． 填空题1．(1)(12)i i -+= ____________. . 2．全集{1,2,3,4}U =，若{1,2},{1,4}A B ==，则()UA B =______________． 3．抛物线214x y =的焦点坐标是 ____________. .4．一个几何体的三视图如图所示，则该几何体的体积等于____________. 5.已知函数)2009(.4)20091(,2log log )(32f f b a x f x x 则若=+-=的值为 . 6.若1(,),sin 2,4216ππθθ∈=则cos sin θθ-的值是 .7. 已知等比数列{}na 的各项均为正数，若31=a ，前三项的和为21 ，则=++654a a a8．阅读如图所示的程序框，若输入的n2 2 2 2 主左2 俯第42n < 否 是开输入S←那么，其中正确命题的个数是二，解答题15. 已知c b a,,分别是ABC∆中角C B A,,的对边，且222+-=A CB A Csin sin sin sin sin（1）求角B的大小；（2）若3c a=，求tan A的值．16.在四棱锥P－ABCD中，四边形ABCD是梯形，AD∥BC，∠ABC=90°，平面PAB⊥平面ABCD，平面PAD⊥平面ABCD.（1）求证：PA⊥平面ABCD；（2）若平面PAB平面PCD l=，问：直线l能否与平面ABCD平行？请说明理由.17. 某企业为打入国际市场，决定从A 、B 两种产品中只选择一种进行投资生产．已知投资生产这两种产品的有关数据如下表：（单位：万美元）项 目 类 别 年固定 成本 每件产品 成本 每件产品 销售价 每年最多可 生产的件数A 产品 20m 10 200 B 产40818120DCA PB品其中年固定成本与年生产的件数无关，m为待定常数，其值由生产A产品的原材料价格决定，预计]8,6[ m．另外，年销售x件B产品时需上交20.05x万美元的特别关税．假设生产出来的产品都能在当年销售出去．（Ⅰ）写出该厂分别投资生产A、B两种产品的年利润,y y与生产相应产品的件数x之间的函12数关系并指明其定义域；（Ⅱ）如何投资才可获得最大年利润？请你做出规划．18. 中心在原点，焦点在x 轴上的椭圆C 的焦距为2，两准线问的距离为10．设A(5,0)， B(1，0)(1)求椭圆C 的方程；(2)过点A 作直线与椭圆C 只有一个公共点D ，求过B ，D 两点，且以AD 为切线的圆 的方程；(3)过点A 作直线l 交椭圆C 于P ，Q 两点，过点P 作x 轴的垂线交椭圆C 于另一点S ． 若→AP=t →AQ （t ＞1），求证：→SB=t →BQ19. 已知函数11()3x p f x -=，22()23x p f x -=⋅（12,,x R p p ∈为常数）．函数()f x 定义为：对每个给定的实数x ，112212(),()()()(),()()f x f x f x f x f x f x f x ≤⎧=⎨>⎩若若（1）求1()()f x f x =对所有实数x 成立的充分必要条件（用12,p p 表示）；（2）设,a b 是两个实数，满足a b <，且12,(,)p p a b ∈．若()()f a f b =，求证：函数()f x 在区间[,]a b 上的单调增区间的长度之和为2b a -（闭区间[,]m n 的长度定义为n m-）20. 已知数列{}na 中，,11=a且点()()*+∈N n a a P n n1,在直线1=+-y x 上。

西安中学、高新一中、交大附中、师大附中、长安一中高2010届第一次模拟考试数学（理）试题命题人：陕西师大附中 李 涛 审题人：西安高新一中 杨天旭一、选择题：本题共10小题，每小题5分，共50分.1．复数2(1)i i+=（ ） A ．2i - B ．2i + C ．2- D ．2 2．命题p ：“对任意一个实数x ，均有20x ≥”，则p ⌝为（ ） A ．存在R x ∈，使得20x ≤ B ．对任意R x ∈，均有20x ≤C ．存在R x ∈，使得20x <D ．对任意R x ∈，均有20x <3．已知向量(cos ,sin )p A A = ,(cos ,sin )q B B =-，若A ，B ，C 是锐角ABC ∆的三个内角，则p 与q的夹角为（ ）A ．锐角B ．直角C ．钝角D ．以上都不对4.若函数321()(1)243f x x a x x =+-+-的导函数/()f x 在区间（－∞，4] 上是减函数，则实数a 的取值范围是（ ）A ．(,3)-∞-B ．(,3]-∞-C ．(3,)-+∞D ．[3,)-+∞5. 双曲线2222143x y -=的右焦点到直线y =的距离是（ ）A ．B ．CD ．6．函数)10(1||log )(<<+=a x x f a 的图象大致为（ ）俯视图侧视图正视图7．某单位有六个科室，现从人才市场招聘来4名新毕业的大学生，要安排到其中的两个科室且每科室2名，则不同的安排方案种数为（ ）A ．2426C AB ．2426A AC ．262A D ．242621C A 8．已知不等式组0,0210x y x y ≥≥⎧⎨+-≤⎩表示平面区域D ．现在往抛物线22y x x =-++与x 轴围成的封闭区域内随机地抛掷一粒小颗粒，则该颗粒落到区域D 中的概率为（ ）A ．19B ．118C ．13D ．169.对任意R x ∈，恒有1110(21)(1)(1)(1)n n n n n x a x a x a x a --+=+++++++ 成立，则数列{}n a 的前n 项和为（ ）A ．1B ．1(1)n +-C ．1(1)n --D ．(1)n -10. 设()f x 是连续的偶函数，且当0x >时()f x 是单调函数，则满足3()4x f x f x +⎛⎫= ⎪+⎝⎭的所有x 之和为（ ）A ．3-B ．3C ．8-D ．8二．填空题：本大题共5小题，每小题5分，共25分. 11.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示，则这个棱柱的体积为 .12．有一个容量为56的样本数据，分组后，组距与频数如下：[0，5）3个，[5，10）5个，[10,15)7个，[15,20)11个，[20,25)12个，[25,30)9个，[30,35)5个，[35,40)4个，则样本在区间[15，35）上的频率为 .（分数表示）13．如果执行下面的程序框图,那么输出的S 等于 .14．给出定义：若2121+≤<-m x m (其中m 为整数)，则m 叫做离实数x 最近的整数，记作}{x ，即m x =}{. 在此基础上给出下列关于函数|}{|)(x x x f -=的四个命题：①函数)(x f y =的定义域是R ，值域是[0，21]；②函数)(x f y =的图像关于直线)(2Z k kx ∈=对称；③函数)(x f y =是周期函数，最小正周期是1；④ 函数)(x f y =在⎥⎦⎤⎢⎣⎡-21,21上是增函数.则其中真命题是__ ．（请填写序号） 15．（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分．）A ．（坐标系与参数方程选做题）在极坐标系中，两点(3,)3A π，2(4,)3B π间的距离是 .B ．（不等式选讲选做题）若不等式125x x ++->的解集为 .C ．（几何证明选讲选做题）如图，点,,A B C 是圆O 上的点， 且6,120BC BAC =∠= ，则圆O 的面积等于 ．三．解答题：本大题共6小题，满分75分.16. （本小题满分12分）已知函数())cos()f x x x ωϕωϕ=+-+（0πϕ<<，0ω>）为偶函数，且函数()y f x =图象的两相邻对称轴间的距离为π2． （Ⅰ）求ω和ϕ的值；（Ⅱ）将函数()y f x =的图象向右平移π6个单位后，得到函数()y g x =的图象，求()g x 的单调递减区间．17．（本小题满分12分）从四名男生和三名女生中任选3人参加演讲比赛． （Ⅰ）求所选3人中至少有一名女生的概率；（Ⅱ）ξ表示所选参加演讲比赛的人员中男生的人数，求ξ的分布列和数学期望.18．（本小题满分12分）如图所示，四棱锥P ABCD -中，底面ABCD 为正方形， PD ⊥ 平面ABCD ，2PD AB ==，E ，F ，G 分别为PC 、PD 、BC 的中点．（Ⅰ）求证：PA EF ⊥；（Ⅱ）求二面角D FG E --的余弦值. 19．（本小题满分12分）在等比数列｛a n ｝中，首项为1a ，公比为q ，n S 表示其前n 项和．（Ⅰ）记n S =A ，2n n S S -= B ，32n n S S -= C ，证明A ，B ，C 成等比数列； （Ⅱ）若111[,]20101949a a =∈，639SS =，记数列2{log }n a 的前n 项和为n T ，当n 取何值时，n T 有最小值．20. (本小题满分13分)已知椭圆 C 的焦点在 x 轴上，一个顶点的坐标是(0,1)，离心率等于552． （Ⅰ）求椭圆 C 的方程；（Ⅱ）过椭圆 C 的右焦点F 作直线 l 交椭圆 C 于,A B 两点，交 y 轴于M 点，若1λ=，2λ=，求证： 21λλ+ 为定值．21．(本小题满分14分)设函数()ln()f x x x m =-+，其中m 为实常数. （Ⅰ）当m 为何值时,()0f x ≥；（Ⅱ）证明:当1m >时,函数()f x 在2[,]m m e m e m ---内有两个零点.GFEPD CBA。