九年级数学上册第4章锐角三角函数4.1-4.3同步练习新版湘教版

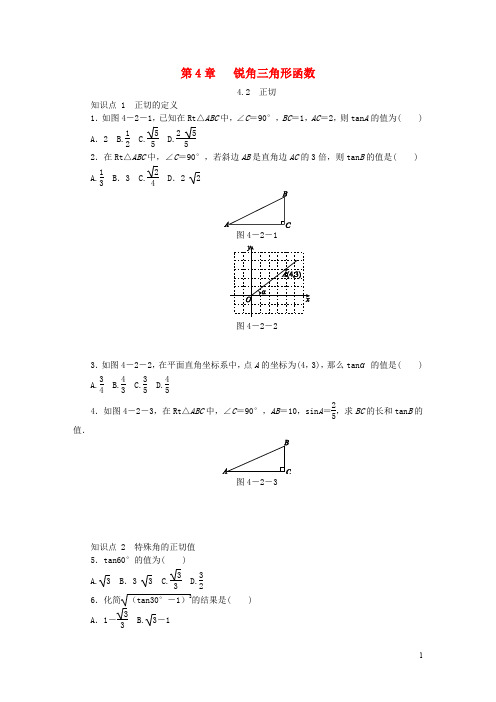
第4章 锐角三角形函数4.2 正切知识点 1 正切的定义 1．如图4－2－1，已知在Rt△ABC 中，∠C ＝90°，BC ＝1，AC ＝2，则tan A 的值为( ) A ．2 B.12 C.55 D.2 552．在Rt△ABC 中，∠C ＝90°，若斜边AB 是直角边AC 的3倍，则tan B 的值是( ) A.13 B ．3 C.24D ．2 2图4－2－1图4－2－23．如图4－2－2，在平面直角坐标系中，点A 的坐标为(4，3)，那么tan α的值是( ) A.34 B.43 C.35 D.454．如图4－2－3，在Rt△ABC 中，∠C ＝90°，AB ＝10，sin A ＝25，求BC 的长和tan B 的值．图4－2－3知识点 2 特殊角的正切值 5．tan60°的值为( ) A. 3 B ．3 3 C.33 D.326．化简（tan30°－1）2的结果是( ) A ．1－33B.3－1C.33－1 D.3＋1 7．计算：(1)tan 230°－2tan60°sin60°＋3tan45°；(2)3sin60°－2cos30°－tan60°·tan45°.知识点 3 用计算器求正切值或角度8．用计算器计算tan44°的结果是(精确到0.01)( ) A ．0.95 B ．0.96 C ．0.97 D ．0.989．已知tan A ＝5.2137，那么锐角A ≈________．(精确到1°) 知识点 4 锐角三角函数10．如图4－2－4，在Rt△ABC 中，∠C ＝90°，AB ＝13，BC ＝12，则下列三角函数表示正确的是( )图4－2－4A ．sin A ＝1312B ．cos A ＝1213C ．tan A ＝512D ．tan B ＝51211．已知α为锐角，且cos α＝35，求sin α，tan α的值．12．李红同学遇到了这样一道题：3tan(α＋20°)＝1，则锐角α的度数应是( ) A ．40° B．30° C．20° D．10° 13．在△ABC 中，若锐角∠A ，∠B 满足|cos A －32|＋(1－tan B )2＝0，则∠C 的度数为( ) A ．45° B．60° C．75° D．105°14．2017·怀化模拟已知在Rt△ABC 中，∠C ＝90°，tan B ＝43，则cos A ＝________．15．如图4－2－5，在△ABC 中，AB ＝AC ＝5，BC ＝8.若∠BPC ＝12∠BAC ，则tan∠BPC ＝________．图4－2－5图4－2－616．如图4－2－6，在菱形ABCD 中，DE ⊥AB 于点E ，cos A ＝35，则tan∠DBE 的值是________．17．计算：(1)sin 245°＋tan60°·cos30°2cos45°＋tan45°；(2)sin60°－1tan60°－2tan45°－3cos30°＋2sin45°.18．如图4－2－7，△ABC的顶点都是正方形网格中的格点，求tan∠BAC的值．图4－2－719．在Rt△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，∠C＝90°.若定义cot A＝∠A的邻边∠A的对边＝ba，则称它为锐角A的余切．根据这个定义解答下列问题：(1)求cot30°的值；(2)已知∠A为锐角，tan A＝34，试求cot A的值；(3)求证：tan A＝cot(90°－∠A)．1．B 2.C3．A [解析] 过点A 作AB 垂直x 轴于点B ，则AB ＝3，OB ＝4，所以tan α＝AB OB ＝34.故选A.4．解：∵sin A ＝BC AB ＝25，AB ＝10，∴BC ＝4.又∵AC ＝AB 2－BC 2＝221， ∴tan B ＝ACBC ＝212. 5．A 6.A 7．解：(1)原式＝(33)2－2 3×32＋3＝13－3＋3＝13. (2)原式＝3×32－2×32－3×1＝3 32－3－3＝－32. 8．C [解析] tan44°≈0.97. 9．79°10． D [解析] ∵∠C ＝90°，AB ＝13，BC ＝12， ∴AC ＝AB 2－BC 2＝5.选项A 中，sin A ＝BC AB ＝1213，错误；选项B 中，cos A ＝AC AB ＝513，错误；选项C 中，tan A ＝BCAC＝125，错误；选项D 中，tan B ＝AC BC ＝512，正确．故选D. 11．解：如图所示，∵cos α＝AC AB ＝35，∴设AC ＝3a ，AB ＝5a (a ＞0)，则BC ＝AB 2－AC 2＝（5a ）2－（3a ）2＝4a ，∴sin α＝BC AB ＝4a 5a ＝45，tan α＝BC AC ＝4a 3a ＝43.12．D [解析] ∵3tan(α＋20°)＝1，∴tan(α＋20°)＝33.∵α为锐角，∴α＋20°＝30°，α＝10°.故选D.13．D [解析] ∵锐角∠A ，∠B 满足|cos A －32|＋(1－tan B )2＝0，∴∠A ＝30°，∠B ＝45°，∴∠C ＝105°.故选D.14.45 [解析] 如图，由tan B ＝43，可设AC ＝4k ，BC ＝3k (k ＞0)，由勾股定理，得AB ＝5k ，∴cos A ＝AC AB ＝4k 5k ＝45.故答案为45.15.4316.2 17．解：(1)原式＝（22）2＋3×322×22＋1＝1.(2)原式＝32－13－2×1－3×32＋2×22＝12－32＋1＝0. 18．解：设小正方形的边长为1，延长AC 与网格交于点E ，连接BE ， 由勾股定理，得BE ＝2，AE ＝3 2，AB ＝2 5，则BE 2＋AE 2＝AB 2，所以△ABE 为直角三角形，且∠AEB ＝90°，所以tan∠BAC ＝BE AE ＝23 2＝13.19． (1)在Rt△ABC 中，∠C ＝90°，设∠A ＝30°，则AB ＝2BC ，AC ＝3BC ， ∴cot30°＝AC BC＝3BCBC＝ 3.(2)在Rt△ABC 中，∠C ＝90°，∵tan A ＝BC AC ＝34，∴可设BC ＝3k (k ＞0)，则AC ＝4k ，∴cot A ＝AC BC ＝4k 3k ＝43.(3)证明：在Rt△ABC 中，∠C ＝90°，则∠A ＋∠B ＝90°，即∠B ＝90°－∠A . ∵tan A ＝BC AC ，cot B ＝BC AC，∴tan A ＝cot B ，即tan A ＝cot(90°－∠A )．。

第4章锐角三角函数一、选择题1.tan60°的值等于（）A. B. C. D.2.在Rt△ABC中，∠C=90o，AC=4，AB=5，则sinB的值是 ( )A. B. C. D.3.如果∠α是等腰直角三角形的一个锐角，则cosα的值是（）A. B. C. 1 D.4.如图，某水渠的横断面是等腰梯形，已知其斜坡AD的坡度为1：1.2，斜坡BC的坡度为1：0.8，现测得放水前的水面宽EF为3.8米，当水闸放水后，水渠内水面宽GH为6米．则放水后水面上升的高度是（）米．A. 1.2B. 1.1C. 0.8D. 2.25.在△ABC中，∠C=90°，AB=15，sinA=，则BC等于（）A. 45B. 5C.D.6.王芳同学从A地沿北偏西60°方向走100m到B地，再从B地向正南方向走200m到C地，此时王芳同学离A地（）A. 50mB. 100mC. 150mD. 100m7.计算sin45°的结果是( )A. B. 1 C. D.8.某地下车库出口处安装了“两段式栏杆”，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图所示的位置，其中AB⊥BC，EF∥BC，∠AEF=135°，AB=AE=1.3米，那么适合该地下车库的车辆限高标志牌为（栏杆宽度忽略不计．参考数据：≈1.4）（）A. B. C. D.9.如图，延长RT△ABC斜边AB到点D，使BD=AB，连接CD，若tan∠BCD=，则tanA=（）A. B. 1 C. D.10.如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽6米，坝高20米，斜坡AB的坡度i=1：2.5，斜坡CD的坡角为30度，则坝底AD的长度为（）A. 56米B. 66米C. （56+20）米D. （50+20）米二、填空题11.若，则锐角α=________．12.一条斜坡长4米，高度为2米，那么这条斜坡坡比i=________ ．13.如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，CD=4，cosA=，那么BC=________14.如图,河堤横断面如图所示,迎水坡AB的坡比为1：,则坡角∠A的度数为________15.在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=________.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)16.如图，从热气球C处测得地面A、B两点的俯角分别为30°、45°，如果此时热气球C处的高度为200米，点A、B、C在同一直线上，则AB两点间的距离是________米（结果保留根号）．17.在Rt 中，，，则的值为________．18.在正方形网格中，△ABC的位置如图所示，则tanB的值为________．19.如图是某品牌太阳能热水器的实物图和横断面示意图，已知真空集热管AB与支架CD所在直线相交于水箱横截面⊙O的圆心，支架CD与水平面AE垂直，AB=150厘米，∠BAC=30°，另一根辅助支架DE=76厘米，∠CED=60°．则垂直支架CD的长度为________厘米（结果保留根号）．三、解答题20.如图，已知∠B=90°，AB=2cm，BC=2cm，CD=3cm，AD=5cm，求四边形ABCD的面积．21.马航MH370 客机“失联”，我国“海巡01号”前往搜寻。

第四章锐角三角函数4.1 正弦和余弦第1课时正弦1（北京市平谷区期末）1．在Rt△ABC中，∠C=90°，∠A=30°，则sin30︒的值是A．1 2B．2C．2D．2（北京市平谷区期末）3．在Rt△ABC中，∠C=90°，AC=4，BC=3，则sin A是A．3 5B．4 5C．3 4D．4 33（北京市房山区期末）3．在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，则sin B的值等于A.3 4B．4 3C．3 5D．4 54（北京市密云县期末）5.如图，在Rt ABC∆，90C∠=︒，8AC=，6BC=，则sin B 的值等于A ．34B ． 34 C ．45D ． 35 5（北京市延庆县期末）6．在Rt △ABC 中，∠C ＝90°，若ABBC ＝2，则sin B 的值为ABC ．12D ．24.2 正弦和余弦第2课时 特殊角的正弦、用计算器求锐角的正弦1.用计算器求sin15°，正确的按键顺序是（ ）A ．sin15=B ．sin15C.Shift15D ．15sin☆2.下面四个数中，最大的是（ ）A ．B ． s in88°C ． s in46°D ．★3.四位学生用计算器求sin62°20′的值正确的是（ ）AA．0.8857 B．0.8856 C．0.8852 D．0.8851★4.（齐齐哈尔）在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，CD=4，AC=6，则sinB的值是____．★5.因为sin30°=，sin210°=﹣，所以sin210°=sin（180°+30°）=﹣sin30°，因为sin45°=，sin225°=﹣，所以sin225°=sin（180°+45°）=﹣sin45°；由此猜想、推理知：一般地，当α为锐角时有sin（180°+α）=﹣sinα，由此可知：sin240°=．4.1 正弦和余弦第3课时余弦1.如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，若AC=2，AB=3，那么cos ∠BCD的值为．2.如图，在Rt△ABC中，∠C=90°，AB=6，cosB=，则BC的长为．3如图，△ABC中，∠C=90°，AC=3，AB=5，则sinA=______，cosA=．4.在△ABC中，∠C=90°，BC=24cm，cosA=513，求这个三角形的周长．4.2 正切1.如图，△ABC中，∠C=90°，AC=5，BC=12，则tanA=______．2.在△ABC中，∠C=90°，AC=4，BC=3，则tanA的值是（）A．B．C．D．3.如图，在3×3的正方形的网格中标出了∠1，则tan∠1的值为（）A ．B．C．D．4.如图，在直角坐标系中，点A的坐标是（2，3），则tanα的值是（）A．B ．C．D．4.在Rt△ABC中，∠C=90°，若AC=5，tanA=2，则BC=．6.如图，已知梯形ABCD中，AB∥CD，AB⊥BC，且AD⊥BD，若CD=1，BC=3，那么∠A的正切值为．7.在△ABC中，∠C=90°，BC=8cm，tanA=，求AC的长．4.3 解直角三角形1（北京市顺义区期末）如图，在△ABC中，D为AB边上一点，B ACD∠=∠，若4AD=，3BD=，求AC的长．AB C D2（北京市顺义区期末） 如图，△ABC 中，∠B =60°，∠C =75°，AC =AB 的长．AB C3（辽宁省鞍山市期末）如图，在四边形ABCD 中，AD ∥BC ，CA 是∠BCD 的平分线，且AB ⊥AC ，AB=4，AD=6，（1）求证：三角形ADC 为等腰三角形；（2）求AC 的长．4（北京市房山区期末）如图，在ABC ∆中，90C ︒∠=，52sin =A ，D 为AC 上一点，45BDC ︒∠=，6=DC ，求AD 的长.5（北京市密云县期末）如图，在DEF ∆中，2,4,120EF DE DEF ==∠=︒， 求DF 的第20题图 C BA4.4 解直角三角形的应用第1课时仰角、俯角问题1.如图，小方在五月一日假期中到郊外放风筝，风筝飞到C 处时的线长为20米，此时小方正好站在A处，并测得∠CBD=60°，牵引底端B离地面1.5米，求此时风筝离地面的高度（结果精确到个位）2.如图，在活动课上，小明和小红合作用一副三角板来测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，他调整自己的位置，设法使得三角板的一条直角边保持水平，且斜边与旗杆顶端M在同一条直线上，测得旗杆顶端M仰角为45°；小红眼睛与地面的距离（CD）是1.5m，用同样的方法测得旗杆顶端M的仰角为30°．两人相距28米且位于旗杆两侧（点B、N、D在同一条直线上）．求出旗杆MN的高度．（参考数据：，，结果保留整数．）3.如图，小明为了测量小山顶的塔高，他在A处测得塔尖D的仰角为45°，再沿AC方向前进73.2米到达山脚B处，测得塔尖D的仰角为60°，塔底E的仰角为30°，求塔高．（精确到0.1米，≈1.732）4.我市某中学在创建“特色校园”的活动中，将本校的办学理念做成宣传牌（AB），放置在教学楼的顶部（如图所示）．小明在操场上的点D处，用1米高的测角仪CD，从点C测得宣传牌的底部B的仰角为37°，然后向教学楼正方向走了4米到达点F处，又从点E测得宣传牌的顶部A的仰角为45°．已知教学楼高BM=17米，且点A，B，M在同一直线上，求宣传牌AB的高度（结果精确到0.1米，参考数据：≈1.73，sin37°≈0.60，cos37°≈0.81，tan37°≈0.75）．4.4 解直角三角形的应用第2课时 坡度、坡比问题 1.如图，已知一商场自动扶梯的长l 为13米，高度h 为5米，自动扶梯与地面所成的夹角为θ，则tanθ的值等于（ ）A ．512B ． 125C ．513D ．12132.（深圳中考）小明去爬山，在山脚看山顶角度为30°，小明在坡比为5:12，的山坡上走1300米，此时小明看山顶的角度为60°，求山高（ ）A ．600-B ．250C ．350+D ．3. （上海中考）已知传送带与水平面所成斜坡的坡度i=1：2.4，如果它把物体送到离地面10米高的地方，那么物体所经过的路程为_____米.☆4. 如图，某公园入口处原有三级台阶，每级台阶高为20cm ，深为30cm ，为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A ，斜坡的起始点为C ，现设计斜坡的坡度i=1：5，则AC的长度是_________.5．（莱芜中考）如图，一堤坝的坡角∠ABC=62°，坡面长度AB=25米（图为横截面），为了使堤坝更加牢固，一施工队欲改变堤坝的坡面，使得坡面的坡角∠ADB=50°，则此时应将坝底向外拓宽多少米？（结果保留到0.01米）（参考数据：sin62°≈0.88，cos62°≈0.47，tan50°≈1.20）☆6.（常德中考）如图，A，B，C表示修建在一座山上的三个缆车站的位置，AB，BC表示连接缆车站的钢缆．已知A，B，C所处位置的海拔AA1，BB1，CC1分别为160米，400米，1000米，钢缆AB，BC分别与水平线AA2，BB2所成的夹角为30°，45°，求钢缆AB和BC的总长度．（结果精确到1米）☆7. （山西中考）如图，点A、B、C表示某旅游景区三个缆车站的位置，线段AB、BC表示连接缆车站的钢缆，已知A、B、C三点在同一铅直平面内，它们的海拔高度AA′，BB′，CC′分别为110米、310米、710米，钢缆AB的坡度i1=1：2，钢缆BC的坡度i2=1：1，景区因改造缆车线路，需要从A到C直线架设一条钢缆，那么钢缆AC的长度是多少米？（注：坡度i是指坡面的铅直高度与水平宽度的比）8.（广安中考）为邓小平诞辰110周年献礼，广安市政府对城市建设进行了整改，如图，已知斜坡AB长米，坡角（即∠BAC）为45°，BC⊥AC，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE 和一条新的斜坡BE（下面两个小题结果都保留根号）．（1）若修建的斜坡BE1，求休闲平台DE的长是多少米？（2）一座建筑物GH距离A点33米远（即AG=33米），小亮在D点测得建筑物顶部H的仰角（即∠HDM）为30°．点B、C、A、G，H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？第4章锐角三角函数一填空题（每小题6分，共18分）：1．在Rt△ABC中，∠C＝90°，a＝2，b＝3，则cos A＝，sin B＝，tan B ＝，cot B＝；2．直角三角形ABC的面积为24cm2，直角边AB为6cm，∠A是锐角，则sin A＝；3．等腰三角形底边长10cm，周长为36cm，则一底角的余切值为.二 选择题：（每题5分，共10分）：1．sin 2θ＋sin 2(90°－θ) (0°＜θ＜90°）等于……………………………………（ ）（A ）0 （B ）1 （C ）2 （D ）2sin 2θ2．ββββcot sin tan cos ⋅⋅ (0°＜β＜90°）等于………………………………………………（ ） （A ）sin β （B ）cos β （C ）tan β （D ）cot β三 计算题（每小题6分，共18分）：1．tan 30°cot 60°＋cos 230°－sin 245°tan 45°2．sin 266°－tan 54°tan 36°＋sin 224°；3．50cos 40sin 0cos 45cot 30cos 330sin 145tan 41222-+-+．四 解直角三角形（△ABC 中，∠C ＝90°，每小题6分，共24分）：1．已知：c ＝ 83，∠A ＝60°，求∠B 、a 、b ．2．已知：a ＝36， ∠A ＝30°，求∠B 、b 、c .6 ，a＝3－1 ，求∠A、∠B、b.3．已知：c＝24．已知：a＝6，b＝23，求∠A、∠B、c.五在直角三角形ABC中，锐角A为30°，锐角B的平分线BD的长为8cm，求这个三角形的三条边的长．六某型号飞机的翼形状如图所示，根据图中数据计算AC、BD和CD的长度（精确到0.1米）．。

湘教版九年级上册数学第4章锐角三角函数含答案一、单选题(共15题，共计45分)1、西周时期，丞相周公旦设置过一种通过测定日影长度来确定时间的仪器，称为圭表。

如图是一个根据北京的地理位置设计的圭表，其中，立柱的高为。

已知，冬至时北京的正午日光入射角约为，则立柱根部与圭表的冬至线的距离（即的长）作为（）A. B. C. D.2、在正方形网格中，△ABC的位置如图所示，则cosB的值为（）A. B. C. D.3、如图，在2×2正方形网格中，以格点为顶点的△ABC的面积等于，则sin∠CAB=（）A. B. C. D.4、如图，某建筑物上挂着“巴山渝水，魅力重庆”的宣传条幅，王同学利用测倾器在斜坡的底部处测得条幅底部的仰角为60°，沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡的坡度米，米（点在同平面内，，测倾器的高度忽略不计），则条幅的长度约为（）（参考数据：）A.12.5米B.12.8米C.13.1米D.13.4米5、在正方形网格中，如图放置，则等于（）A. B. C. D.6、如图所示,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos∠BCD的值是( )A. B. C. D.7、如图，击打台球时小球反弹前后的运动路线遵循对称原理，即小球反弹前后的运动路线与台球案边缘的夹角相等（α=β），在一次击打台球时，把位于点P处的小球沿所示方向击出，小球经过5次反弹后正好回到点P，若台球案的边AD的长度为4，则小球从P点被击出到回到点P，运动的总路程为（）A.16B.16C.20D.208、如图，直线y＝x＋3与x、y轴分别交于A、B两点，则cos∠BAO的值是( )A. B. C. D.9、若∠A为锐角，且cosA<0.5，则∠A（）A.小于30°B.大于30°C.大于60°D.大于60°10、在正方形网格中，∠α的位置如图所示，则tanα的值是（）A. B. C. D.211、如图，的三个项点均在格点上，则的值为（）A. B. C.2 D.12、勾股定理有着悠久的历史，它曾引起很多人的兴趣.英国佩里加（H.Perigal，1801﹣1898）用“水车翼轮法”（图1）证明了勾股定理.该证法是用线段QX，ST，将正方形BIJC分割成四个全等的四边形，再将这四个四边形和正方形ACYZ拼成大正方形AEFB（图2）.若AD＝，tan∠AON＝，则正方形MNUV的周长为（）A. B.18 C.16 D.13、下列选项错误的是（）A. B. C. D.14、如图，轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行，在B处观测灯塔A位于南偏东50°方向上，轮船航行40分钟到达C处，在C 处观测灯塔A位于北偏东10°方向上，则C处与灯塔A的距离是（）A.20海里B.40海里C. 海里D. 海里15、在直角三角形中，各边的长度都扩大到原来的3倍，则锐角A的三角函数值（）A.都扩大到原来的3倍B.都缩小为原来的3倍C.都保持原来的数值都不变D.有的变大，有的缩小二、填空题(共10题，共计30分)16、如图，在一笔直的海岸线l上有A、B两个观测站，AB=2km，从A测得船C 在北偏东45°的方向，从B测得船C在北偏东22.5°的方向，则船C离海岸线l的距离（即CD的长）为________．17、△ABC中，∠C=90°，AB=8，cosA=，则BC的长________18、如图，把两张宽度都是3cm的纸条交错的叠在一起，相交成角α．则重叠部分的面积为________．19、小颖家住在甲楼，她所居住的楼房前面有一座乙楼。

湘教版2020年九年级上册第4章《锐角三角函数》检测卷满分120分姓名：___________班级：___________学号：___________题号一二三总分得分一．选择题（共12小题，满分36分，每小题3分）1．在Rt△ABC中，∠C＝90°，BC＝5，AC＝12，则sin B的值是（）A．B．C．D．2．已知sin A＝0.9816，运用科学计算器求锐角A时（在开机状态下），按下的第一个键是（）A．B．C．D．3．如图，在△ABC中，∠ACB＝90°，D是AB的中点，若CD＝5，AC＝8，则tan A＝（）A．B．C．D．4．如图，有一斜坡AB的长AB＝10米，坡角∠B＝36°，则斜坡AB的铅垂高度AC为（）A．10tan36°B．10cos36°C．10sin36°D．5．已知cosα＝，则锐角α的取值范围是（）A．0°＜α＜30°B．30°＜α＜45°C．45°＜α＜60°D．60°＜α＜90°6．在Rt△ABC中，∠C＝90°，BC：AB＝5：13，则下列等式正确的是（）A．tan A＝B．sin A＝C．cos A＝D．tan A＝7．sin58°、cos58°、cos28°的大小关系是（）A．cos28°＜cos58°＜sin58°B．sin58°＜cos28°＜cos58°C．cos58°＜sin58°＜cos28°D．sin58°＜cos58°＜cos28°8．如图，△ABC的三个顶点均在格点上，则tan A的值为（）A．B．C．2 D．9．在Rt△ABC中，∠C＝90°，则下列式子定成立的是（）A．sin A＝sin B B．cos A＝cos B C．tan A＝tan B D．sin A＝cos B 10．如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内），已知AB＝a，AD＝b，∠BCO＝x，则点D到OB的距离等于（）A．a sin x+b sin x B．a cos x+b cos xC．a sin x+b cos x D．a cos x+b sin x11．若角α，β都是锐角，以下结论：①若α＜β，则sinα＜sinβ；②若α＜β，则cosα＜cosβ；③若α＜β，则tanα＜tanβ；④若α+β＝90°，则sinα＝cosβ．其中正确的是（）A．①②B．①②③C．①③④D．①②③④12．我国北斗导航装备的不断更新，极大方便人们的出行．某中学组织学生利用导航到C 地进行社会实践活动，到达A地时，发现C地恰好在A地正北方向，导航显示路线应沿北偏东60°方向走到B地，再沿北偏西37°方向走才能到达C地．如图所示，已知A，B两地相距6千米，则A，C两地的距离为（）（参考数据sin53°≈0.80，cos53°≈0.60，tan53°≈1.32）A．12千米B．（3+4）千米C．（3+5）千米D．（12﹣4）千米二．填空题（共6小题，满分24分，每小题4分）13．已知tan（α+15°）＝，则锐角α的度数为°．14．比较大小：sin81°tan47°（填“＜”、“＝”或“＞”）．15．如图，在△ABC中，∠C＝90°，AC＝6，若cos A＝，则BC的长为．16．如图所示，∠AOB是放置在正方形网格中的一个角，则sin∠AOB的值是．17．小致为了测量楼房AB的高度，他从楼底的B处沿着斜坡行走20m，达到坡顶D处．已知斜坡的坡角为15°，小致的身高ED是1.6m，他站在坡顶看楼顶A处的仰角为45°，则楼房AB的高度为m．（计算结果精确到1m，参考数据：sin15°＝，cos15°＝，tan15°＝．）18．如图，BE是△ABC的角平分线，F是AB上一点，∠ACF＝∠EBC，BE、CF相交于点G．若sin∠AEB＝，BG＝4，EG＝5，则S△ABE＝．三．解答题（共7小题，满分60分）19．（12分）计算：（1）2sin30°+3cos60°﹣4tan45°（2）+tan260°20．（6分）如图，锐角△ABC中，AB＝10cm，BC＝9cm，△ABC的面积为27cm2．求tan B 的值．21．（6分）在Rt△ABC中，∠C＝90°，∠A、∠B、∠C的对边分别为a、b、c．若a＝2，sin，求b和c．22．（8分）2019年4月18日，台湾省花莲县发生里氏6.7级地震，救援队救援时，利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象，已知废墟一侧地面上两探测点A、B相距6米，探测线与地面的夹角分别为30°和60°，如图所示，试确定生命所在点C的深度．（结果精确到0.1米，参考数据≈1.41，≈1.73）23．（9分）嘉琪在某次作业中得到如下结果：sin27°+sin283°≈0.122+0.992＝0.9945，sin222°+sin268°≈0.372+0.932＝1.0018，sin229°+sin261°≈0.482+0.872＝0.9873，sin237°+sin253°≈0.602+0.802＝1.0000，sin245°+sin245°＝（）2+（）2＝1．据此，嘉琪猜想：在Rt△ABC中，∠C＝90°，设∠A＝α，有sin2α+sin2（90°﹣α）＝1．（1）当α＝30°时，验证sin2α+sin2（90°﹣α）＝1是否成立．（2）请你对嘉琪的猜想进行证明．24．（9分）如图，小明利用学到的数学知识测量大桥主架在水面以上的高度AB，在观测点C处测得大桥主架顶端A的仰角为30°，测得大桥主架与水面交汇点B的俯角为14°，观测点与大桥主架的水平距离CM为60米，且AB垂直于桥面．（点A，B，C，M在同一平面内）（1）求大桥主架在桥面以上的高度AM；（结果保留根号）（2）求大桥主架在水面以上的高度AB．（结果精确到1米）（参考数据sin14°≈0.24，cos14°≈0.97，tan14°≈0.25，≈1.73）25．（10分）已知△ABC，AB＝AC，∠BAC＝90°，D是AB边上一点，连接CD，E是CD 上一点，且∠AED＝45°．（1）如图1，若AE＝DE，①求证：CD平分∠ACB；②求的值；（2）如图2，连接BE，若AE⊥BE，求tan∠ABE的值．参考答案一．选择题（共12小题，满分36分，每小题3分）1．解：如图所示：∵∠C＝90°，BC＝5，AC＝12，∴AB＝＝13，∴sin B＝＝．故选：D．2．解：∵已知sin A＝0.9816，运用科学计算器求锐角A时（在开机状态下）的按键顺序是：2ndF，sin，0，∴按下的第一个键是2ndF．故选：D．3．解：∵∠ACB＝90°，D是AB的中点，CD＝5，∴AB＝2CD＝10，∵AC＝8，AB＝10，∴BC＝＝6，∴tan A＝＝＝．故选：C．4．解：在Rt△ABC中，sin B＝，∴AC＝AB•sin B＝10sin36°，故选：C．5．解：∵cos30°＝，cos45°＝，∵＜＜，∴30°＜α＜45°，6．解：设BC＝5x，则AB＝13x，由勾股定理得，AC＝＝12x，则tan A＝＝，A、D错误；sin A＝＝，B错误；cos A＝＝，C正确；故选：C．7．解：sin58°＝cos32°．∵58°＞32°＞28°，∴cos58°＜cos32°＜cos28°，∴cos58°＜sin58°＜cos28°．故选：C．8．解：如图所示：连接BD，BD＝＝，AD＝＝2，AB＝＝，∵BD2+AD2＝2+8＝10＝AB2，∴△ADB为直角三角形，∴∠ADB＝90°，则tan A＝＝＝．故选：A．9．解：∵∠C＝90°，∴∠A+∠B＝90°，∴sin A＝cos B．10．解：如图，过点D作DE⊥OC于点E，则点D到OB的距离等于OE的长．∵四边形ABCD是矩形，∴∠BCD＝90°，CD＝AB＝a，AD＝BC＝b，∴∠CDE＝∠BCO＝x，∴OC＝BC•cos x＝b cos x，CE＝CD•sin x＝a sin x，∴OE＝OC+CE＝b cos x+a sin x．则点D到OB的距离等于b cos x+a sin x．故选：C．11．解：①∵sinα随α的增大而增大，∴若α＜β，则sinα＜sinβ，此结论正确；②∵cosα随α的增大而减小，∴若α＜β，则cosα＞cosβ，此结论错误；③∵tanα随α的增大而增大，∴若α＜β，则tanα＜tanβ，此结论正确；④若α+β＝90°，则sinα＝cosβ，此结论正确；综上，正确的结论为①③④，故选：C．12．解：如图，作BD⊥AC于点D，根据题意可知：在Rt△ADB中，∠A＝60°，AB＝6，∴AD＝3，BD＝3，在Rt△CDB中，∠CBD＝53°，∴CD＝BD•tan53°≈3×1.32≈3×≈4，∴AC＝AD+CD＝3+4．则A，C两地的距离为（3+4）千米．故选：B．二．填空题（共6小题，满分24分，每小题4分）13．解：∵tan30°＝，∴α+15°＝30°，∴α＝15°，故答案为：15．14．解：∵sin81°＜sin90°＝1，tan47°＞tan45°＝1，∴sin81°＜1＜tan47°，∴sin81°＜tan47°．故答案为＜．15．解：∵在△ABC中，∠C＝90°，AC＝6，cos A＝，∴cos A＝＝＝，∴AB＝10，∴BC＝＝＝＝8．故答案为：8．16．解：如图，连接AB．∵OA＝AB＝，OB＝2，∴OB2＝OA2+AB2，∴∠OAB＝90°，∴△AOB是等腰直角三角形，∴∠AOB＝45°，∴sin∠AOB＝，故答案为：．17．解：作DH⊥AB于H，∵∠DBC＝15°，BD＝20m，∴BC＝BD•cos∠DBC＝20×＝19.2（m），CD＝BD•sin∠DBC＝20×＝5（m），由题意得，四边形ECBF和四边形CDHB是矩形，∴EF＝BC＝19.2m，BH＝CD＝5m，∵∠AEF＝45°，∴AF＝EF＝19.2m，∴AB＝AF+FH+HB＝19.2+1.6+5＝25.8≈26（m），答：楼房AB的高度约为26m．故答案是：26．18．解：如图，过点B作BT⊥AC于T，连接EF．∵BE平分∠ABC，∴∠ABE＝∠CBE，∵∠ECG＝∠ABE，∴∠ECG＝∠CBE，∵∠CEG＝∠CEB，∴△ECG∽△EBC，∴＝＝，∴EC2＝EG•EB＝5×（5+4）＝45，∵EC＞0，∴EC＝3，在Rt△BET中，∵sin∠AEB＝＝，BE＝9，∴BT＝，∴ET＝＝＝，∴CT＝ET+CE＝，∴BC＝＝＝6，∴CG＝＝10，∵∠ECG＝∠FBG，∴E，F，B，C四点共圆，∴∠EFG＝∠CBG，∵∠FGE＝∠BGC，∴△EGF∽△CGB，∴＝，∴＝，∴EF＝3，∵∠AFE＝∠ACB，∠EAF＝∠BAC，∴△EAF∽△BAC，∴＝＝＝，设AE＝x，则AB＝2x，∵∠FBG＝∠ECG，∠BGF＝∠CGE，∴△BGF∽△CGE，∴＝，∴＝，∴BF＝，∵AE•AC＝AF•AB，∴x（x+3）＝（2x﹣）•2x，解得x＝，∴AE＝ET＝，∴点A与点T重合，∴AB＝2AE＝，∴S△ABE＝×AB×AE＝××＝．故答案为．三．解答题（共7小题，满分60分）19．解：（1）原式＝＝＝；（2）原式＝＝+3＝．20．解：过点A作AH⊥BC于H，∵S△ABC＝27，∴，∴AH＝6，∵AB＝10，∴BH＝＝＝8，∴tan B＝＝＝．21．解：如图，∵a＝2，sin，∴c＝＝＝6，则b＝＝＝4．22．解：过点C作CD⊥AB，交AB的延长线于D，在Rt△ACD中，∠CAD＝30°，tan∠CAD＝，∴AD＝＝CD，在Rt△ACD中，∠CBD＝60°，tan∠CBD＝，∴BD＝＝CD，由题意得，AD﹣BD＝AB＝6，∴CD﹣CD＝6，解得，CD＝3≈5.2（米），答：生命所在点C的深度约为5.2米．23．解：（1）当α＝30°时，sin2α+sin2（90°﹣α）＝sin230°+sin260°＝（）2+（）2＝+＝1；（2）嘉琪的猜想成立，证明如下：如图，在△ABC中，∠C＝90°，设∠A＝α，则∠B＝90°﹣α，∴sin2α+sin2（90°﹣α）＝（）2+（）2＝＝＝1．24．解：（1）∵AB垂直于桥面，∴∠AMC＝∠BMC＝90°，在Rt△AMC中，CM＝60，∠ACM＝30°，tan∠ACM＝，∴AM＝CM•tan∠ACM＝60×＝20（米），答：大桥主架在桥面以上的高度AM为20米；（2）在Rt△BMC中，CM＝60，∠BCM＝14°，tan∠BCM＝，∴MB＝CM•tan∠BCM≈60×0.25＝15，∴AB＝AM+MB＝15+20≈50（米）答：大桥主架在水面以上的高度AB约为50米．25．（1）①证明：∵AE＝DE，∴∠ADE＝∠DAE，∵∠CAD＝90°，∴∠ADC+∠ACD＝90°，∠DAE+∠CAE＝90°，∴∠CAE＝∠ACD，∴EA＝EC，∵∠AED＝45°＝∠CAE+∠ACD，∴∠ACD＝22.5°，∵AB＝AC，∠BAC＝90°，∴∠ACB＝45°，∴∠BCD＝∠ACD＝22.5°，∴CD平分∠ACB．②解：如图1中，过点D作DT⊥BC于T．∵CD平分∠ACB，DT⊥CB，DA⊥CA，∴DA＝DT，∵AB＝AC，∠BAC＝90°，∴∠B＝45°，∴BD＝DT＝AD，∴＝．（2）解：如图2中，连接BE，过点C作CT⊥AT交AE的延长线于T．∵AE⊥BE，CT⊥AT，∴∠AEB＝∠T＝∠BAC＝90°，∴∠BAE+∠ABE＝90°，∠BAE+∠CAE＝90°，∴∠ABE＝∠CAT，∵AB＝AC，∴△ABE≌△CAT（AAS），∴AE＝CT，BE＝AT，∵∠AED＝∠CET＝45°，∠T＝90°，∴ET＝CT＝AE，∴BE＝2AE，∴tan∠ABE＝＝。

湘教版数学九年级上册 第4章 锐角三角形 4.3 解直角三角形 同步练习题1．如图，已知Rt △ABC 中，∠C ＝90°，AC ＝4，tanA ＝12，则BC 的长是( )A ．2B ．8C ．2 5D ．4 52．如图是教学用直角三角板，边AC ＝30 cm ，∠C ＝90°，tan ∠BAC ＝33，则边BC 的长为( )A ．30 3 cmB ．20 3 cmC ．10 3 cmD ．5 3 cm3．在直角三角形ABC 中，已知∠C＝90°，∠A ＝40°，BC ＝3，则AC ＝( ) A ．3sin40° B ．3sin50° C ．3tan40° D ．3tan50° 4．在Rt △ABC 中，∠C ＝90°，若a ＝6，∠B ＝30°，则c 和tanA 的值分别为( ) A ．12，33 B ．12， 3 C ．43，33D ．22， 3 5．如图，某游乐场一山顶滑梯的高为h, 滑梯的倾斜面与水平面的夹角为α，那么滑梯长l 为( )A.h sin αB.h tan αC.h cos α D ．h ·sin α 6．如图，在Rt △ABC 中，∠C ＝90°.(1)已知∠A 和c ，则a ＝_____________，b ＝_____________. (2)已知∠B 和b ，则a ＝_________，c ＝____________．7．在Rt △ABC 中，∠C ＝90°，且∠A，∠B ，∠C 的对边分别为a ，b ，c. (1)已知c ＝6，∠A＝60°，则a ＝_______，b ＝____； (2)已知a ＝4，∠B ＝45°，则b ＝____，c ＝________； (3)已知a ＝10，b ＝103，则c ＝_______，∠A ＝______； (4)已知b ＝63，c ＝12，则a ＝____，∠B ＝________. 8．在Rt △ABC 中，∠C ＝90°，根据下列条件解直角三角形： (1)∠A ＝30°，b ＝12；(2)a ＝26，c ＝4 3.9．直角三角形ABC 中，∠B ＝90°，∠C ＝30°，AB ＝3.求AC 和BC 的长．10．如图，小明为了测量其所在位置A 点到河对岸B 点之间的距离，沿着与AB 垂直的方向走了m 米，到达点C ，测得∠ACB ＝α，那么AB 等于( )A ．m ·sin α米B ．m ·tan α米C ．m ·cos α米 D.m tan α米11．在Rt △ABC 中，∠C ＝90°，sinA ＝513，则tanB 的值为( )A.1213B.512C.1312D.12512．在Rt △ABC 中，∠C ＝90°，若AB ＝4，sinA ＝35，则斜边上的高等于( )A.6425B.4825C.165D.12513．在Rt △ABC 中，∠C ＝90°，sinB ＝32，a ＝5，则∠B＝______，c ＝______．14．如图，△ABC 中，AD ⊥BC ，垂足为点D ，若BC ＝14，AD ＝12，tan ∠BAD ＝34，求sinC 的值．15．如图，在Rt △ABC 中，∠C ＝90°，AC ＝8，∠BAC 的平分线AD ＝1633，求∠B 的度数及边BC ，AB 的长．16．如图，在Rt △ABC 中，∠C ＝90°，AC ＝ 3.点D 为BC 边上一点，且BD ＝2AD ，∠ADC ＝60°，求△ABC 的周长．(结果保留根号)17．如图，在△ABC中，∠ABC＝90°，∠A＝30°，D是边AB上一点，∠BDC ＝45°，AD＝4，求BC的长．(结果保留根号)18．如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝23，求AB的长．答案:1—5 ACDDA6. (1) c·sinA c·cosAbsinB7. (1) 3 3 3 (2) 4 4 2 (3) 20 30° (4) 6 60°8. (1) 解：∠B＝60°，AB ＝83，BC ＝4 3(2) 解：b ＝26，∠A＝45°，∠B＝45°9. 解：sin30°＝AB AC ＝3AC ，∴AC＝6，∴BC＝AC 2－AB 2＝3 310. B 11. D 12. B13. 60° 1014. 解：∵tan ∠BAD ＝BD AD ，∴34＝BD12，∴BD ＝9，CD ＝5，AC ＝AD 2＋CD 2＝13，sinC ＝AD AC ＝121315. 解：cos ∠CAD ＝CA AD ＝81633＝32，∴∠CAD ＝30°，∴∠BAC ＝60°，∴∠B ＝30°，tan ∠B ＝AC BC ，∴33＝8BC ，∴BC ＝83，sin ∠B ＝AC AB ，∴12＝8AB，∴AB ＝16 16. 解：在Rt△ACD 中，AC ＝3，∠ADC＝60°，∴AD＝AC sin60°＝3sin60°＝2，∴BD＝2AD ＝4，CD ＝1，∴AB＝（3）2＋52＝28＝27.∴c △ABC ＝27＋5＋ 317. 解：tanA ＝BC AB ，∴AB＝BC tan30°＝3BC ，tan∠BDC＝BCBD ，∴BD＝BC tan45°＝BC ，AB －BD ＝AD ，即(3－1)BC ＝4，∴BC＝43－1＝2(3＋1)18. 解：过点C 作CD⊥AB 于点D.在Rt△ACD 中，∵∠A＝30°，∴CD＝12AC ＝3，由勾股定理得AD ＝（23）2－（3）2＝9＝3，在Rt△BCD 中，∵tan45°＝CDBD ，∴BD＝CD ＝3.∴AB＝AD ＋BD ＝3＋ 3。