下载文档原格式
课堂探究探究一与杨辉三角有关的问题解决与杨辉三角有关的问题一般方法是观察法，观察时可以横看、竖看、斜看等多角度观察，找出数据之间的关系．由特殊到一般推出对应规律，用数学式子表达出来，并进行简单说明所得规律的正确性．【典型例题1】如图所示,在杨辉三角中，第n条和第(n＋1）条细斜线上各数之和与第（n＋2）条细斜线上各数之和的关系如何?证明结论．思路分析:此题可先从特殊行得出结论，然后再证明其一般性，如令n＝2,去探究第2条和第3条细斜线上各数之和与第4条细斜线上各数之和的关系．解：第n条和第(n＋1）条细斜线上各数之和等于第(n＋2）条细斜线上各数之和．证明如下：第n条细斜线上各数之和为C错误!＋C错误!＋C错误!＋C错误!＋C错误!＋…，第(n＋1）条细斜线上各数之和为C0n＋C错误!＋C错误!＋C错误!＋C错误!＋C错误!＋…，故这两条细斜线上各数之和为(C错误!＋C错误!＋C错误!＋C错误!＋C错误!＋…)＋(C错误!＋C错误!＋C错误!＋C错误!＋C错误!＋C错误!＋…）＝C错误!＋（C错误!＋C错误!)＋（C错误!＋C错误!）＋(C错误!＋C错误!）＋(C错误!＋C错误!）＋…＝C错误!＋C错误!＋C错误!＋C错误!＋C错误!＋….等式右边正好是第（n＋2)条细斜线上各数之和,所以第n条和第（n＋1)条细斜线上各数之和与第（n＋2）条细斜线上各数之和相等．探究二求展开式的各项系数之和赋值法是求二项展开式系数及有关问题的常用方法，取值要有利于问题的解决，可以取一个值或几个值，也可以取几组值,解决问题时要避免漏项．一般地，对于多项式f(x）＝a0＋a1x＋a2x2＋…＋a n x n，各项系数和为f(1)．奇次项系数和为错误
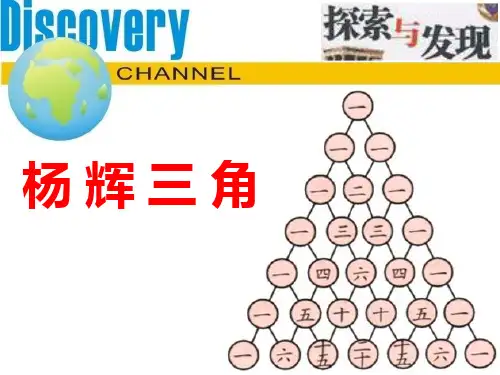
《杨辉三角》之初探在学习生活中，我们常常会遇到这个三角形，它的名字叫做杨辉三角。
它和赵爽弦图、割圆术一样，是我国古代数学的骄傲。
那么，杨辉三角有什么奥秘呢？让我们来一探究竟吧！图1一、探究规律探究1如图1：看横排杨辉三角中各行数字有怎样的数字规律？发现1：每一横行的首尾两项都是1，且两头对称分布；发现2：每一行的数字个数为与行数相同；发现3：杨辉三角中第n行数字的和为2n-1;探究2看竖排上下两行数字有什么关系？发现1：除1外的每一个数都等于它肩上两个数的和；发现2：我们发现，从第二行开始，每一行的第二个数分别为1，2，3，……，是一个公差为1的等差数列，思考：每一行的第三个数组成的数列1,3,6，10，15又有什么规律呢？=1a1=1+2a2a3=1+2+3……由此我们不难发现，an =1+2+3+……+n，所以an=，也就是说，第三项其实是一个二阶等差数列；第四项有什么性质呢？……二、拓展延伸延伸1：仔细观察，杨辉三角其实是也呈现二项式系数规律。
如：思考：按照前面的规律，则（a+b）5展开后结果如何？．（由图3可知，二项式展开后的项数比指数多1，当a的次数在增加时，b的次数反而减小，但每一项的次数都为5）延伸2：如图4：斜线上各行数字的和，有什么规律？（从第三个数起，任一数都等于前两个数的和，这就是著名的斐波那契数列，也称为兔子数列）延伸3：如图5：（a+b）8的展开式中从左起第四项的系数为多少？（不难得出第四项的系数可以转化为前一行之前所有的第三个数之和）延伸4：以此类推（a+b）n的展开式中中间第系数又为多少？……杨辉三角中远远不只这些规律，需要我们不断的探索。
通过对杨辉三角的探究，我更进一步认识到杨辉三角的美妙，也发现了杨辉三角中隐藏的一些数字规律，同时也深刻理解了中国古代数学的智慧。
更重要的是，我学会了探索数学的奥秘。
这将对我的教学能力会有很大的帮助和提升，我将在今后的教学中，用我的好奇心和勇于探索的品质对待每一个数学问题。
探究数学秘密，发现数学之美——“杨辉三角〞中的一些秘密一、教材背景分析1．教材的地位和作用“杨辉三角〞是我国古代数学重要成就之一，显示了我国古代人民的卓越智慧和才能，应抓住这一题材，对学生进行爱国主义教育，鼓励学生的民族自豪感。
2．学情分析本节课面对的是高二年级的学生,这个年龄段的学生思维活泼,求知欲强,但在思维习惯上还有待教师引导。
通过之前的学习学生已经掌握了分类加法计数原理和分步乘法计数原理,理解了排列、组合的概念,掌握了二项式定理和二项展开式的性质。
同时对于数形结合、类比、转化的数学思想方法也有了初步的认识。
对于本节探究与发现的研究性学习,可以激发学生学习热情,提高课堂效率,使知识得到螺旋式的稳固与提高。
而对于加强学生自身对于数学的应用意识及实际问题的分析能力方面,还有待于教师的指导帮助。
学生根据教师提供的情境,采用观察、分析、抽象、概括等方式探索知识,归纳知识。
通过创设情境疑问,引导学生开展独立思考、主动探究、合作交流,探求解决问题的方法。
鼓励学生创新思考,加强数学实践,培养学生的理性思维,同时注重培养学生良好的数学学习习惯。
3．教学重点与难点重点:掌握二项式展开式的性质,理解二项展开式的系数与杨辉三角之间的联系。
难点:通过探究杨辉三角的规律,初步体验数学中“合情推理〞、“归纳假设〞等研究问题的数学方法。
二、教学目标新课标指出教学目标应表达学生学会知识与技能的过程,也要同时表达学生学会学习形成正确价值观的过程。
结合本节课的教学内容,制定如下教学目标:1．通过课前组织学生开展“了解杨辉三角、探究与发现杨辉三角包含的规律〞的学习活动，让学生感受我国古代数学成就及其数学美，激发学生的民族自豪感。
2．掌握二项式展开式的性质,理解二项展开式的系数与杨辉三角之间的联系。
3．通过探究杨辉三角的规律,初步体验数学中“合情推理〞、“归纳假设〞等研究问题的数学方法。
4．采用学生课前自主探究、课上合作探究、课下延伸探究的学习方式，培养学生问题意识，提高学生思维能力，孕育学生创新精神，激发学生探索、研究我国古代数学的热情。
杨辉三角原理
嘿，朋友们！今天咱来聊聊超有意思的杨辉三角原理！你知道不，这杨辉三角就像是一个神奇的魔法阵。
咱就说，你看那杨辉三角，一层一层的，多像我们小时候叠的纸金字塔呀！每一行的数字都有它独特的规律，就好像它们在悄悄告诉我们什么秘密一样。
比如说，从最上面开始，每层的数字两边都是 1，这就好像一个守护宝物的卫士，坚定地站在那里！然后呢，中间的数字可就有趣啦，它们是上一行相邻两个数字之和。
哎呀呀，这可不是一般的厉害呀！
有一次，我和小伙伴一起研究杨辉三角，我们就像是探险的小伙伴，试图解开这个神秘三角的谜团。
我们一个数一个数地看，一个规律一个规律地找，那种投入的感觉，简直太棒啦！我当时就在想，这杨辉三角背后到底隐藏着多少奇妙的东西呢？
它可不只是一堆数字的排列哦！它在数学、科学甚至艺术领域都有广泛的应用呢！这不就和我们生活中的很多小事物一样吗？看似普通，实则蕴含着巨大的能量。
杨辉三角就像是一个智慧的宝库，等待我们去不断挖掘。
你难道不想去探索一下吗？你不想知道它还能给我们带来哪些惊喜和启示吗？我觉得呀，我们应该好好去研究它，去发现它更多的美妙之处。
相信我，一旦你深入了解了杨辉三角原理，你一定会被它深深地吸引，就像我一样，对它充满着好奇和喜爱！
总之，杨辉三角原理真的太神奇、太有趣啦！大家可别错过这个探索的好机会哦！。
《探究与发现“杨辉三角”中的一些秘密》教学设计教学设计：探究与发现“杨辉三角”中的一些秘密一、教学目标：1.知识目标：了解杨辉三角的特点和生成规律。
2.能力目标：能够用递推关系式生成杨辉三角的任意一行。
3.情感目标：培养学生对于数学问题的探究和发现兴趣，培养学生的合作意识和动手实践能力。
二、教学重点和难点：1.教学重点：掌握生成杨辉三角的关系式。
2.教学难点：理解关系式的推导过程，发现杨辉三角中的一些秘密。
三、教学过程：1.导入（5分钟）通过提问带入话题，引发学生对于杨辉三角的思考：你们知道杨辉三角是什么吗？它有什么特点？它能怎么用呢？2.探究与发现（25分钟）1)指导学生用列表的方式生成杨辉三角的前6行，让他们观察并总结规律。
2)让学生猜测生成杨辉三角的规律，并与同桌合作讨论并得出结论。
3)引导学生找出每一行与下一行之间的关系，并推导出生成杨辉三角的递推关系式。
3.团体合作（20分钟）学生分成小组，在老师的指导下进行团体合作，探索杨辉三角中的一些秘密。
1)让学生探索杨辉三角中的规律并总结，如每一行的和、每一行的最大值等。
2)让学生进一步探索杨辉三角中的数的特性，如每一行数字的2次方和3次方之和、每一行数字的素数和等。
4.总结与拓展（10分钟）1)让学生回顾讨论的内容，总结出杨辉三角中一些特点和秘密。
2)带领学生拓展思考，进一步研究杨辉三角中的数学问题，如杨辉三角在组合数学中的应用。
5.归纳与反思（5分钟）学生归纳总结本节课学到的知识和技能，通过合作学习探究的方式对杨辉三角的生成规律和特点有了更深入的了解。
四、教学资源准备：1.杨辉三角的生成表格或展示材料。
2.小组合作讨论的工具或材料。
五、教学评价：1.观察学生在探究过程中的参与程度和合作情况。
2.检查学生对于杨辉三角的递推关系式的掌握情况。
3.回顾学生的总结和拓展，评价学生对学习内容的理解和掌握程度。
六、教学反思：本节课通过探究与发现的方式，让学生参与到探索杨辉三角的过程中，培养了他们的探究能力和合作意识。
杨辉三角的规律以及推导公式杨辉三角规律下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!杨辉三角的规律及推导公式引言杨辉三角是中国古代数学宝库中的一颗璀璨明珠，它展现了一种神奇的数学规律，被广泛应用于代数、组合数学、概率论等领域。
浅谈杨辉三角奥秘及应用杨辉三角是由中国古代数学家杨辉在13世纪前提出的一种数学模型，它以三角形的形式展示了关于二项式系数的一些重要性质和规律。
这个三角形被称为杨辉三角，因为这个数学模型最早由杨辉所研究。
杨辉三角被广泛应用于数学、概率、组合数学等领域，其奥秘和应用价值都是十分重要的。
首先，让我们来看一下杨辉三角的构造规则。
杨辉三角的第一行是数字1，每一行的两端也是数字1。
从第二行开始，每个数是上一行两个数的和。
用数学语言描述，杨辉三角的第n行第i个数（从第0项开始数）等于第n-1行第i-1个数和第i个数的和。
用公式表示为：C(n,i) = C(n-1,i-1) + C(n-1,i)这个规则使得杨辉三角的每一行都符合二项式展开式中各项的系数。
例如，第4行的数字依次为1, 3, 3, 1，对应的二项式展开式为(a+b)^3 = 1a^3 + 3a^2b + 3ab^2 + 1b^3。
当然，这只是杨辉三角的一个应用之一。
杨辉三角的奥秘在于它有许多隐藏的规律和特性，这些规律和特性不仅仅在数学中有用，也在其他领域中有广泛的应用。
以下是杨辉三角的几个重要的规律和特性：1. 对称性规律：杨辉三角是关于中心对称的，即三角形的左半边与右半边是完全相同的。
这个对称性特性使得杨辉三角在概率和组合数学中有重要的应用。
例如，计算二项式系数时，如果我们知道了C(n,i)，则C(n,n-i) = C(n,i)，这个特性在组合计数中非常有用。
2. 斜线规律：从三角形的顶点到底边的任何一条斜线上的数字之和，都是由2的幂次方所组成的序列。
例如，斜线上的数字之和依次为1, 2, 4, 8, 16...，这个规律在计算组合数学中有着重要的应用。
3. 杨辉三角与二项式展开：正如我们之前提到的，杨辉三角中的每一行都符合二项式展开式中各项的系数。
这个特性使得在不知道n的具体值的情况下，可以直接根据杨辉三角的对应行来展开一个二项式。
杨辉三角的应用十分广泛。
浅谈杨辉三角的奥秘及应用摘要文中阐述了杨辉三角中蕴涵的一些优美的规律及利用杨辉三角在以其为背景的一些现实生活问题中的应用来培养解决问题的思维能力。
关键词杨辉三角，最短路径，错位，幂0 引言杨辉是我国南宋末年的一位杰出的数学家。
在他著的《详解九章算法》一书中，画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现在简称为“杨辉三角"，它是杨辉的一大重要研究成果。
随着素质教育的提倡，新课程标准的颁布，生活中很多问题都与杨辉三角有着或多或少的联系，那如何解决这些以“杨辉三角”为背景的问题呢？这就需要我们对杨辉三角本身蕴涵着许多优美的规律进行探讨和研究。
1 杨辉三角与数字11的幂的关系我们知道初中时老师要求我们背11的幂，11的1次幂、2次幂、3次幂还好背，后面就难起来了。
后来我受到一位老师的启发,并且查看了这方面有关资料，发现杨辉三角与11的n次幂的关系非常密切.假设y=11n当n=0时: y=1；当n=1时： y=11；当n=2时：y=121；当n=3时：y=1331；当n=4时: y=14641；以上是当n≤4时与扬辉三角的前5行多一致，接下来我们再来看一下当n≥5时的情况，如下：当n=5时: 1 4 6 4 1⨯ 1 11 4 6 4 11 4 6 4 11 5 10 10 5 1当n=6时： 1 5 10 10 5 1⨯ 1 11 5 10 10 5 11 5 10 10 5 11 6 15 20 15 6 1……由上可知:11的n 次幂的各位数字（不含进位）与杨辉三角中的各数字完全相等(证明还有待证明)即杨辉三角是11的幂按错位相加不进位的方法依次从小到大排列而成的图形。
如下图：1 (110) 1 1 (111）1 2 1 (112）1 3 3 1 (113)1 4 6 4 1 （114)1 5 10 10 5 1 （115）1 6 15 20 15 6 1 （116) ……其实这个关系我们早就学习过了,只是用另一种方式表达而已。
