参考椭球面

参考椭圆体名词解释
参考椭球体，也被称为“参考扁球体”或“参考椭圆体”，是由椭圆绕其短轴旋转形成的形体。

它具有确定的形状和大小，并且经过定位和定向。

在大地测量学中，参考椭球体是一个数学上定义的地球表面，它近似于大地水准面。

与某个区域如一个国家的大地水准面最为密合的椭球面，称为该区域的参考椭球体。

在测量和制图上，人们采用一个非常接近大地体的旋转椭球体作为地球的参考形状和大小。

通常所说地球的形状和大小，实际上就是以参考椭球体的半长径、半短径和扁率来表示。

以上内容仅供参考，可以查阅关于椭球体的专业书籍或者咨询天文学家以获取更多更准确的信息。

题目：解密参考椭球面、大地水准面和海平面一、引言在地理测量和地球科学领域，参考椭球面、大地水准面和海平面是极其重要的概念和工具。

它们不仅对于地图绘制、航海、建筑工程等有着重要的应用，更深层次地影响着人们对于地球形状、重力场和海洋水文等方面的认识。

本文将深入探讨这些概念的内涵、相互关系以及其实际应用，帮助读者更加全面地了解地球和地理测量学的奥秘。

二、参考椭球面1. 参考椭球面的定义和作用参考椭球面是一种以椭圆形状来近似地球的三维曲面，用于描述地球的精确形状。

它是地球表面地理坐标系的基础，如经纬度系统就是以参考椭球面为基准来确定点的位置。

参考椭球面的选择对于地图绘制和导航有着重要的影响，不同的参考椭球面会导致地图上的形状和面积产生不同程度的变形。

2. 世界上常用的参考椭球面目前，世界上常用的参考椭球面包括国际椭球体、WGS84椭球和克拉索夫斯基椭球等。

它们在地图制图、GPS定位和地球物理测量等领域均有着广泛的应用。

三、大地水准面1. 大地水准面的概念和特点大地水准面是地球重力场潮汐作用下的平均形态所确定的水准面。

它是一个复杂的曲面，通常被定义为重力位势等值面。

大地水准面是地球形状研究和大地测量的基础，对于确定地球的形状、重力场和大地测量学参数具有重要意义。

2. 大地水准面与参考椭球面的关系大地水准面和参考椭球面是地球表面形状的两个重要描述。

它们之间的关系虽然复杂，但可以简单理解为参考椭球面是地图的基础，而大地水准面则是地球形状的基础。

地图上标注的海拔高度实际上是相对于大地水准面的高度，而经纬度是相对于参考椭球面坐标系的位置。

四、海平面1. 海平面的定义和测量方式海平面是海洋潮汐作用下确定的平均水平面，是地球表面的一个特殊曲面。

海平面的测量通常采用卫星高度计、测潮仪和GPS等技术手段，以实现对海平面的精确测量和监测。

2. 海平面的应用和意义海平面的稳定变化对于气候变化、海洋科学和海岸防护等都有着重要的影响。

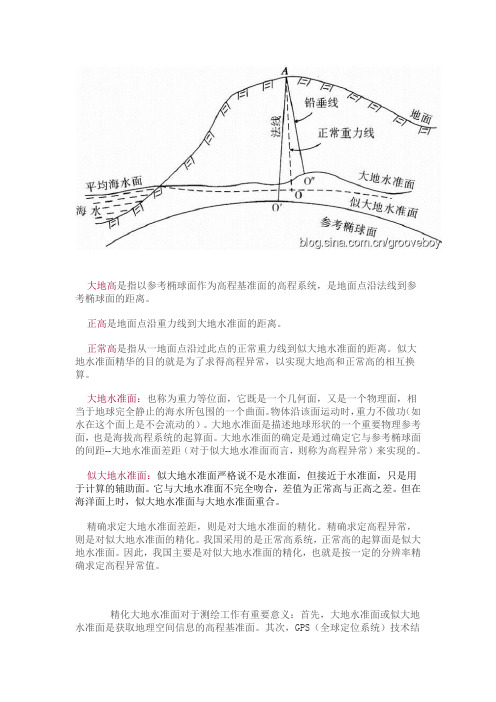
大地高是指以参考椭球面作为高程基准面的高程系统，是地面点沿法线到参考椭球面的距离。

正高是地面点沿重力线到大地水准面的距离。

正常高是指从一地面点沿过此点的正常重力线到似大地水准面的距离。

似大地水准面精华的目的就是为了求得高程异常，以实现大地高和正常高的相互换算。

大地水准面：也称为重力等位面，它既是一个几何面，又是一个物理面，相当于地球完全静止的海水所包围的一个曲面。

物体沿该面运动时，重力不做功（如水在这个面上是不会流动的）。

大地水准面是描述地球形状的一个重要物理参考面，也是海拔高程系统的起算面。

大地水准面的确定是通过确定它与参考椭球面的间距--大地水准面差距（对于似大地水准面而言，则称为高程异常）来实现的。

似大地水准面：似大地水准面严格说不是水准面，但接近于水准面，只是用于计算的辅助面。

它与大地水准面不完全吻合，差值为正常高与正高之差。

但在海洋面上时，似大地水准面与大地水准面重合。

精确求定大地水准面差距，则是对大地水准面的精化。

精确求定高程异常，则是对似大地水准面的精化。

我国采用的是正常高系统，正常高的起算面是似大地水准面。

因此，我国主要是对似大地水准面的精化，也就是按一定的分辨率精确求定高程异常值。

精化大地水准面对于测绘工作有重要意义：首先，大地水准面或似大地水准面是获取地理空间信息的高程基准面。

其次，GPS（全球定位系统）技术结合高精度高分辨率大地水准面模型，可以取代传统的水淮测量方法测定正高或正常高，真正实现GPS技术对几何和物理意义上的三维定位功能。

再次，在现今GPS 定位时代，精化区域性大地水准面和建立新一代传统的国家或区域性高程控制网同等重要，也是一个国家或地区建立现代高程基准的主要任务，以此满足国家经济建设和测绘科学技术的发展以及相关地学研究的需要。

近年来，我国经济发达地区及中、小城市，在地形图测绘方面，对厘米级似大地水准面的需求十分迫切。

高精度的似大地水准面结合GPS定位技术所获得的三维坐标中的大地高分离求解正常高，可以改变传统高程测量作业模式，满足1：1万、1：5000甚至更大比例尺测图的迫切需要，加快数字中国、数字区域、数字城市等的建设，不但节约大量人力物力，产生巨大的经济效益，而且具有特别重要的科学意义和社会效益。

参考椭球面和大地水准面英文回答：Ellipsoid and Geoid are two important concepts in geodesy and geodetic surveying. The ellipsoid is a mathematical model that approximates the shape of the Earth, while the geoid represents the true shape of the Earth's surface, taking into account the irregularities caused by variations in gravity and the distribution of mass.The ellipsoid is often referred to as a reference surface because it provides a convenient and consistent framework for measuring and representing the Earth's surface. It is defined by its semi-major axis (equatorial radius) and semi-minor axis (polar radius). The most commonly used ellipsoid model is the World Geodetic System 1984 (WGS84), which is widely adopted for globalpositioning systems (GPS) and mapping applications.In contrast, the geoid is a surface of equalgravitational potential that closely approximates mean sea level. It represents the equipotential surface to which the oceans would conform under the influence of gravity alone, assuming no other forces such as tides and currents. The geoid is irregular and undulates due to variations in gravity caused by differences in the Earth's mass distribution. It is used as a reference surface for measuring elevations and determining orthometric heights.To understand the relationship between the ellipsoid and the geoid, imagine the ellipsoid as a smooth surface that fits the Earth's shape without considering the irregularities. The geoid, on the other hand, takes into account these irregularities and represents the true shape of the Earth's surface. The difference between theellipsoid and the geoid, known as the geoid undulation or geoidal separation, varies from place to place and can be positive or negative.The ellipsoid and the geoid are connected through a mathematical transformation known as the geodetic datum. A geodetic datum defines the position and orientation of theellipsoid relative to the Earth's surface, allowing for accurate geodetic measurements and coordinate systems. Different countries and regions may use different datums, which can result in variations in coordinates and elevations.In practical terms, the ellipsoid is used for navigation, mapping, and satellite positioning systems. For example, when using a GPS device to determine your location, the coordinates provided are based on the ellipsoid model. On the other hand, the geoid is used for determining orthometric heights, which are heights above mean sea level. This is important for applications such as flood modeling, construction, and aviation.In conclusion, the ellipsoid and the geoid are two fundamental concepts in geodesy. The ellipsoid provides a convenient mathematical model for representing the Earth's shape, while the geoid represents the true shape, takinginto account irregularities caused by gravity and mass distribution. The relationship between the two is established through a geodetic datum. Understanding thedifference between the ellipsoid and the geoid is crucialfor accurate geodetic measurements and applications.中文回答：椭球面和大地水准面是大地测量和测量工程中的两个重要概念。

高程系统在测量中常用的高程系统有大地高系统、正高系统和正常高系统。

一、大地高系统大地高系统是以参考椭球面为基准面的高程系统。

某点的大地高是该点到通过该点的参考椭球的法线与参考椭球面的交点间的距离。

大地高也称为椭球高，大地高一般用符号H表示。

大地高是一个纯几何量，不具有物理意义，同一个点，在不同的基准下，具有不同的大地高。

二、正高系统正高系统是以大地水准面为基准面的高程系统。

某点的正高是该点到通过该点的铅垂线与H表示。

大地水准面的交点之间的距离，正高用符号g三、正常高正常高系统是以似大地水准面为基准的高程系统。

某点的正常高是该点到通过该点的铅垂H表示。

线与似大地水准面的交点之间的距离，正常高用γ四、高程系统之间的转换关系图1 高程系统间的相互关系h。

大地高与正高之间的大地水准面到参考椭球面的距离，称为大地水准面差距，记为g关系可以表示为：g g h H H +=似大地水准面到参考椭球面的距离，称为高程异常，记为ζ。

大地高与正常高之间的关系可以表示为：ζγ+=H HGPS 高程的方法由于采用GPS 观测所得到的是大地高，为了确定出正高或正常高，需要有大地水准面差距或高程异常数据。

五、 等值线图法从高程异常图或大地水准面差距图分别查出各点的高程异常ζ或大地水准面差距g h ，然后分别采用下面两式可计算出正常高γH 和正高g H 。

正常高： ζγ-=H H正高： g g h H H -=在采用等值线图法确定点的正常高和正高时要注意以下几个问题：⏹ 注意等值线图所适用的坐标系统，在求解正常高或正高时，要采用相应坐标系统的大地高数据。

⏹ 采用等值线图法确定正常高或正高，其结果的精度在很大程度上取决于等值线图的精度。

六、 地球模型法地球模型法本质上是一种数字化的等值线图，目前国际上较常采用的地球模型有OSU91A 等。

不过可惜的是这些模型均不适合于我国。

七、 高程拟合法1. 基本原理所谓高程拟合法就是利用在范围不大的区域中，高程异常具有一定的几何相关性这一原理，采用数学方法，求解正高、正常高或高程异常。

参考椭球面和大地水准面
参考椭球面和大地水准面是两个重要的测地学概念，它们都是用来描述地球形状的数学模型。

参考椭球面是一个规则的椭球体，其形状和大小由长半轴、短半轴和扁率三个参数决定。

参考椭球面是大地测量中常用的基准面，用来表示地球的形状和大小。

大地水准面是一个与地球重力等位面相重合的曲面，也就是说，在大地水准面上，重力的大小和方向都是相同的。

大地水准面是描述地球形状和大小的另一种重要基准面。

一、两者的区别
参考椭球面和大地水准面之间存在着以下区别：
1．形状：参考椭球面是一个规则的椭球体，而大地水准面是一个不规则的曲面。

2．大小：参考椭球面的形状和大小由长半轴、短半轴和扁率三个参数决定，而大地水准面的形状和大小是由地球的实际形状和大小决定的。

3．用途：参考椭球面主要用于大地测量中，用来表示地球的形状和大小，而大地水准面主要用于水准测量中，用来表示高程。

二、两者之间的关系
参考椭球面和大地水准面之间存在着密切的关系，它们之间可以通过大地水准面差距来联系起来。

大地水准面差距是指大地水准面与参考椭球面之间的距离，其值在不同地区有所不同。

三、以下是一些有关参考椭球面和大地水准面的知识：
1．地球的形状并不是完美的球形，而是一个略扁的球体。

2．参考椭球面是用来近似地球形状的数学模型。

3．大地水准面是地球重力的等位面。

4．大地水准面在不同地区的高度有所不同。

5．大地水准面差距是大地水准面与参考椭球面之间的距离。

测量中常用的坐标系一、坐标系类型1、大地坐标系定义：大地测量中以参考椭球面（不准确）为基准面建立起来的坐标系。

一定的参考椭球和一定的大地原点上的大地起算数据，确定了一定的坐标系。

通常用参考椭球参数和大地原点上的起算数据作为一个参心大地坐标系建成的标志。

大地坐标（地理坐标）：将某点投影到椭球面上的位置用大地经度L和大地纬度B表示，（ B ， L）统称为大地坐标。

大地高H：某点沿投影方向到基准面（参考椭球面）的距离。

在大地坐标系中，某点的位置用（B ， L，H）来表示。

2、空间直角坐标系定义：以椭球体中心为原点，起始子午面与赤道面交线为X 轴，在赤道面上与X轴正交的方向为Y轴，椭球体的旋转轴为Z轴。

在空间直角坐标系中，某点的位置用（X，Y，Z）来表示。

3、平面直角坐标系在小区域进行测量工作若采用大地坐标来表示地面点位置是不方便的，通常采用平面直角坐标系。

测量工作以x轴为纵轴，以y轴为横轴投影坐标：为了建立各种比例尺地形图的控制及工程测量控制，一般应将椭球面上各点的大地坐标按照一定的规律投影到平面上，并以相应的平面直角坐标表示。

4、地方独立坐标系基于限制变形、方便、实用和科学的目的，在许多城市和工程测量中，常常会建立适合本地区的地方独立坐标系，建立地方独立坐标系，实际上就是通过一些参数来确定地方参考椭球与投影面。

二、国家大地坐标系1.1954年北京坐标系（BJ54旧）坐标原点：前苏联的普尔科沃。

参考椭球：克拉索夫斯基椭球。

平差方法：分区分期局部平差。

存在问题：（1）椭球参数有较大误差。

（2）参考椭球面与我国大地水准面存在着自西向东明显的系统性倾斜。

（3）几何大地测量和物理大地测量应用的参考面不统一。

（4）定向不明确。

2.1980年国家大地坐标系（GDZ80）坐标原点：陕西省泾阳县永乐镇。

参考椭球：1975年国际椭球。

平差方法：天文大地网整体平差。

特点：（1）采用1975年国际椭球。

（2）参心大地坐标系是在1954年北京坐标系基础上建立起来的。