95.青岛版数学七年级下同步作业(六三制)
- 格式:pdf
- 大小:12.18 MB
- 文档页数:83

【本文档由书林工作坊整理发布,谢谢你的下载和关注!】单元测试卷一、选择题1下列时刻中,时针与分针之间的夹角为300的是()A早晨6点 B.下午13点 C.中午12点 D.上午9点2.如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落 E在D'、C'的位置.若∠AE D'=50°,则∠DEF等于()A.50°B.65°C.75°D.60°3将31.62°化成度分秒表示,结果是()A.3106'2''B.31037'12"C.31037'2" D.31°37'4. 如图∠AOC和∠BOD都是直角,如果∠AOB=140°,则∠DOC的度数A.300B.400C.500D.6005. 如果∠α=260,那么∠α余角的补角等于()A.20° B .700 C.110° D.11606. 下列说法中正确的有()(1) 钝角的补角一定是锐角(2) 过己知直线外一点作这条直线的垂线有且只有一条(3) —个角的两个邻补角是对顶角(4) 等角的补角相等(5) 直线l外一点A与直线l上各点连接而成的所有线段中,最短线段的长是3cm,则点A到直线l的距离是3cm .A 2个 B. 3个 C. 4 个 D. 5 个7. 如图,直线a、b、c两两相交,若∠1+∠7=180。
,则图中与∠1互补的角有()A. 1个B. 2个C. 3个D. 4个8. 如图,P0丄OR, 0Q丄PR,能表示点到直线(或线段)的距离的线段有()A. 1条B.2条C.3条D.5条9. 如图,已知ON丄a,OM丄a,所以OM与ON重合的理由是().A. 两点确定一条直线B. 经过一点有且只有一条线段垂直于己知直线C. 过一点只能作一条垂线D. 垂线段最短10. 如果∠1与∠2互为补角,且∠1>∠2,那么∠2的余角是()A.12∠1 B12∠2 C.12∠1-∠2) D.12(∠l+∠2)11. 如果∠A和∠B互为余角,∠B和∠C互为补角,∠A与∠C的和等于1200,那么这三个角分别是()A. 15°, 75°, 105°B. 20°, 70°, 90°C. 300,600,900D. 700,200,100012. 如图, ∠AOB=∠COD,则()A.∠1>∠2B.∠1=∠2C.∠1<∠2D.∠1与∠2的大小无法比较二、填空题13. 如果∠α+∠β=900,而∠β与∠γ互余,那么∠α与∠γ的关系为。

数学练习册七年级下册参考答案8.11.(1)∠A,∠C;(2)∠ABC,∠ABD,∠DBC,∠ADB,∠BDC;(3)3个,∠ABD,∠ABC,∠DBC.2.B.3.(1)∠AEB,∠DAE,∠BEC,∠ADB;(2)∠C,∠D.4.3个角;6个角;10个角.5.9时12分或21时12分.8.21.(1)42°;(2)不变.2.C.3.D.5.46°.提示:设∠COE=x°,则x-8=130-2x,x=46.6.(1)45°;(2)不变;提示:90+2x2-x=45;(3)不变.提示:90-2y2+y=45.8.3第1课时1.(1)42°20′24″;(2)56.35.2.(1)61°38′10″;(2)32.6.3.C.4.C.5.(1)93°12′;(2)47°31′48″;(3)12°9′36″;(4)33°7′12″.6.(1)112°27′;(2)51°55′;(3)125°37′30″.7.0.5°,6°.8.(1)15°;(2)172.5°.9.40分钟.第2课时1.153°.2.53°17′45″.3.C.4.C.5.63°.6.(1)相等;(2)180°.7.60°.8.41.∠3,∠AOD.2.121°.3.C.4.B.5.∠3=25°30′,∠2=45°.6.∠2=63°30′,∠3=53°.7.(1)2对;(2)6对;(3)12对.8.51.70°.2.45°.3.D.4.C.5.132°.6.135°.7.60°,30°.第八章综合练习1.130°.2.36°16′30″.3.50°.4.(1)54°34′,125°26′;(2)α-90°.5.47.6.D.7.A.8.C.9.D.10.138°.11.125°.12.∠AOC+∠BOC=2(∠DOC+∠COE)=2×90°=180°,A,O,B共线.13.设∠BOE=x°,∠EOC=2x°,∠AOB=180-3x,∠DOB=72-x.得方程(72-x)×2=180-3x,解得x=36.即∠EOC=72°.14.∠BOC+∠COD+∠AOD=270°,∠EOF=170°,∠AOE+∠BOF=190°-90°=100°.∠COF+∠DOE=100°.又∠EOF=170°,∠COD=170°-100°=70°.检测站1.45°.2.98.505°.3.∠AOB,∠BOC.∠AOB,∠BOD.4.C.5.D.6.∠BOD,∠FOE,∠BOC;∠BOF.7.45°.8.97.5°.9.11.∠END.2.DE,AB,BC;AB,BC,DE.3.B.4.C.5.∠CAD,∠BAC,∠B.6.同位角:∠EAD与∠B;∠EAC与∠B;内错角:∠DAC与∠C;∠EAC与∠C.同旁内角:∠DAB与∠B;∠BAC与∠B.7.略.9.21.相交,平行.2.不相交.3.一.4.C.5.略.6.略.7.正方形.8.略.9.31.65°,两直线平行,同位角相等,65°,对顶角相等.2.65°.3.B.4.C.5.130°.6.∠B,∠EFC,∠ADE.7.40°.9.4第1课时1.AC,BD,内错角相等,两直线平行.2.(1)EN,BD;(2)AB,CD.3.B.4.∠5=∠2=105°,∠5+∠1=180°.5.DE∥MN.由AB∥MN,DE∥AB.6.提示:由AD∥BC,得∠A+∠B=180°,∠C+∠B=180°,AB∥CD.7.(1)由∠3=∠B,知FD∥AB,知∠4=∠A;(2)由ED∥AC,知∠1=∠C,∠BED=∠A.第2课时1.4厘米.2.BD,BE.3.D.4.由∠B=∠C,知AB∥CD,故∠A=∠D.5.∠1=∠GMC=90°-∠2.6.(1)∠MDF=∠MBE,BE∥DF;(2)不是;它是AB和CD之间的距离.7.在∠B内画射线BF∥AE,则BF∥CD.∠ABF=120°,∠FBC=30°,∠C=180°-30°=150°.第九章综合练习1.110°.2.AD∥BE,BD∥CE,AD∥BE.3.35°.提示:过点M画MN⊥AB,MN∥EG,∠HMN=∠E,∠HMN=90°-∠AMH.4.C.5.C.6.D.7.126°.8.∠1=115°.9.25°.10.∠3=80°,∠4=100°.11.因为AB∥CD,所以∠AEF=∠2,∠AEG=∠3,因为∠AEG=∠1+∠2,所以∠3=∠1+∠2.12.22°.提示:过点A画直线c∥a.检测站1.内错,同旁内,同位.2.180°.3.A.4.B.5.AB∥CD,AD∥BC.6.AD∥BC.DB平分∠ADC代替第二个条件.10.12.5.3.C4.D.6.a=7,b=-9.7.设需要汽车x辆,共有y人外出参观,35x+15=y,45(x-1)=y.解得x=6,y=225..8.不是.10.2第1课时1.-35x+85,-53y+83.2.x-1=0.3.B.4.(1)x=-12,y=52;(2)s=-3,t=-3;(3)m=2,n=1.5.x=1,y=-1.6.提示:按丙的方法,35x=3,25y=4,得x=5,y=10.第2课时1.2.2.-11.3.C.4.B.5.(1)x=-1,y=-8;(2)x=5,y=272.6.令x+y=a,x-y=b,解得a=2,b=-1,又解得x=12,y=32.7.k=4.10.3第1课时1.4x+y=6,-5x+4y=-7.2.C.3.(1)x=1,y=1,z=1;(2)x=1,y=2,z=3.4.解三元一次方程组,用a表示解,得x=a,y=a+1,z=a-1,代入方程-x+2y+3z=6,得a=74.5.将z看做已知数,将x,y解出来.得x=1911-z,y=211-z.x+y+2z=1911-z+211-z+2z=2111.第2课时1.加减,①,②.2.B.3.(1)x=2,y=1,z=-1;(2)x=1,y=2,z=2.4.a=1,b=-1,c=1.10.4第1课时1.7x+3=y,8x-5=y.2.320,180.3.C.4.216,1095.90元,100元.6.5元,3元.7.提示:设小长方形宽x,长y,则5x=3y,y+2x=2y+2,得x=6,y=10.第2课时1.112x=0.5+112y,0.5x=(0.5+1)y.2.30,18.3.D.4.C.5.21张铁皮做盒身,28张铁皮做盒盖.6.长木6.5尺,绳长11尺.7.(1)x+y=90,46%x+70%y=90×64%,x=22.5,y=67.5.(2)46%x+70%y=64%(x+y),x∶y=1∶3.*第3课时1.x+y+z=21,x+y-z=5,x-(z-y)=5.2.4,8,10.3.C.4.2,3,5.5.12,8,7.第十章综合练习1.43.2.-1.3.-112,5,(113,0).4.-14.5.x=1,y=2.6.y=23x-53.7.B.8.A.*9.D.10.(1)x=1,z=2;(2)x=6,y=24;(3)x=3,y=2;*(4)x=2,y=-3,z=-1.11.300棵,200棵.12.50人,220件.13.23.14.中型15辆,小型35辆.15.m=-275.16.30千米,70千米,42千米.17.平均每天1只大牛需用饲料20千克,小牛需用5千克.所以王大伯对大牛食量的估计是正确的,对小牛食量的估计偏高.18.火车速度22米/秒,列车长276米.19.(1)x=2,y=2,也是剩下一个方程的解.(2)不唯一.如x-y=0. 检测站1.-10.2.a=2,b=1.3.5千克,2千克.4.C.5.C.6.a=5.*7.x=1,y=2,z=3.8.牛值金2两,羊值金1两.9.男生270名,女生260名. 11.11.108.2.x12.3.x4.4.D.5.A.6.1.5×108.7.(1)m9;(2)3×1011.8.(1)(a-b)5;(2)-(2x-3y)3n+1.9.0.10.0.11.2第1课时1.-8t3.2.116a4b4.3.-6x2.4.A.5.C.6.(1)28x3y3;(2)anbn;(3)-9a3x3.7.a2b.8.1.9.1102n.10.14位数.第2课时1.(1)x10;(2)-8x12.2.C.3.D.5.(1)19x2y4;(2)215;(3)x12;(4)64m12n6.6.(1)x6n+2;(2)-(a+b)7;(3)35n-2.7.提示:24<33,(24)25<(33)25.11.3第1课时1.12xy3.2.-6x2y3.3.B.4.D.5.(1)m5n2;(2)1.2×1020.6.(1)-14x5y4z2;(2)64x6.7.-730(a-b)8n-4.8.C.第2课时1.3x2-5x3.2.x2-y2.3.D.4.C.5.(1)-3x2y+2xy2-52xy;(2)x4+4x2+2x-4;(3)12b3-b2+6b.6.2m3n3-8m2n3.7.x=-12.8.10.11.4第1课时1.x2-7x+10.2.-6x2-xy+2y2.3.B.4.B.5.(1)-6m2+19m-15;(2)-12x3+14x2-4x;(3)-3y2-23y+108.6.4x2-100x+600.7.-x2-29x+32,1854.8.提示:该代数式的值恒为22. 9.x=-110.b=12.第2课时1.x3+2x2-5x-6.2.2a3+5a2+a-3.3.B.4.C.5.(1)m3+2m2-1;(2)2a3-5a2b+8ab2-3b3;(3)-2x3-x2-7x+10.6.x3+x-5,值为-7.7.x=-12.8.0.11.51.4.2.m8.3.xn.4.D.5.B.6.16.7.(1)-a;(2)a3.8.(1)y-x;(2)(x+2y)6.9.2xy.11.6第1课时1.1.2.1.3.0.4.C.5.D.6.(1)64;(2)a.7.(1)3 129;(2)200.8.7.9.a≠0,m=n.第2课时1.181.2.-164.3.100.4.B.5.C.6.(1)200;(2)10 099;(3)100.7.10-1,10-2,10-3,10-4.8.a<b<d<c.9.x≠-13.10.1.第3课时1.1.2.1a4.3.a8.4.C.5.125.6.(1)10;(2)x5;(3)11 000 000;(4)1a7.7.13a.8.2-101.第4课时1.1.2×10-4.2.0.000 002 76.3.2.5×10-9.4.D.5.D.6.(1)1.5×10-2;(2)2.1×103;(3)1.5×10-3.7.x=-7.8.1.572×104.9.花粉直径较大,是兔毛直径的7.2倍.第十一章综合练习1.106.2.x9.3.a.4.tn.5.(a+b)2.6.x5.7.a7.8.15x3y3z.9.2a3+2a2b+2ab.10.-2x2+3x-1.11.B.12.B.13.B.14.A.15.(1)x9;(2)-(a+b)4;(3)-a2b2+6ab+23a;(4)-6n+2;(5)2a3+8ab2-14a2b;(6)-3x2-23x+108;(7)6x2-13xy;(8)-x13y12.16.(1)-x,1;(2)5x-1,101.17.x=-1.18.(1)x=4;(2)n=2,m=4;(3)M=x2-6x+9.19.2ab+2b2.20.n(n+5)-(n-3)(n+2)=6(n+1).检测站1.(x+y)5.2.-6a3b3c.3.-2x3-4x2+2x.4.a6b6.5.C.6.B.7.B.8.1.24×10-6.9.299.10.(1)36x2-114x+90;(2)91x2-277x+210.11.长8、宽5.12.11.b2-9a2.2.x4-4.3.1681m2n2-49.4.5x+3y.5.C.6.B.7.(1)c2-9a2b2;(2)9y2-4x4;(3)a4-b4;(4)-5x2-9.8.(1)(300+3)(300-3)=90000-9=89 991;(2)1.9.(2n-1)(2n+1)=(2n)2-1.10.原式×3-23-2=332-232.12.2第1课时1.-2ab.2.a2+4ab+4b2.3.k=8.4.B.5.C.6.A.7.(1)9m2-32n+116;(2)x4-2x2+1;(3)a2+2ab+b2;(4)916s2+st+49t2.8.(a+b)2=4ab+(a-b)2.9.a2+2ab+b2=9,a2-2ab+b2=49.ab=14(9-49)=-10.a2+b2=9-2ab=29.第2课时1.4ab.2.a2+b2+c2+2ab-2ac-2bc.3.x2-y2+z2+2xz.4.B.5.B.6.A.7.(1)2a2b2-b4;(2)2y2+2x+ 5;(3)(100-3)(100-1)(100+1)(100+3)=(104-9)(104-1)=108-105+9=99 900 009.8.12.9.48π(a+1).10.8.12.31.2x2y.2.2a4-ab+6.3.a-b-2.4.D.5.C.6.(1)xy(x-y);(2)4ab(bc+4);(3)-2xy(1+2x-4x2);(4 )-(3a+b)(a+3b);(5)2x(x-y)2(1-2x).7.1999.8.14ax(2a-x)2.9.能.256-510=512-510=510(25-1)=24×510.12.4第1课时1.(x+2y)(x-2y).2.k=-140.3.D.4.C.5.(1)(6+x)(6-x);(2)(12y+1)2;(3)-(m-n)2;(4)(3+14a)(3-14a).6.(1)8 056;(2)90 000.7.(1)(1+a+b)(1-a-b);(2)(a-b+2)2.8.左端=[(a-b)2+(a+b)2+(a-b)2-(a+b)2]·[(a-b)2+(a+b)2-(a-b)2+(a+b)2]=4(a-b)2(a+b)2.第2课时1.提出公因式,用公式法进行因式分解.2.x(x+1)(x-1).3.(a-1)(x+y)(x-y).4.D.5.C.6.(1)m(m2+1)(m+1)(m-1).(2)2x3(3y+1)(3y-1).(3)(x+2)2(x-2)2.(4)(x+1)4.7.原式=12·32·23·43·34·54…910·1110=1120.8.2 0122(2 0112-1)+(2 0132-1)=2 0122(2 011+1)(2 011-1)+(2 013+1)(2 013-1)=2 01224 024=1 006.第十二章综合练习1.9x2-y2.2.25-4b2.3.25a2-20ab+4b2.4.14m4+2m2n+4n2.5.-2m.6.x-y+2.7.(xy+2z)(xy-2z).8.23m-0.1n.9.C.10.C.11.C.12.(1)4x2+4xy+y2-25z2;(2)-280y2+1295;(3)116x4-181y4.13.(1)2a3x2(2+a)(2-a);(2)(x-y)(a+2y)(a-2y);(3)-(a-b)2(a+b)2;( 4)(x2+2x+7)(x-1)2.14.(1)31×(573+427)×(573-427)=4 526 000;(2)76 900;(3)10099.15.πR2-4πr2=π(R+2r)(R-2r)=3.14×10× 5.6=175.8厘米.16.(n+7)2-(n-5)2=(n+7+n-5)(n+7-n+5)=24(n+1).17.x=141.18.x=2,y=-3,16.19.(2n+1) 2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=8n.检测站1.2b-3a.2.20或-20.3.5-a2.4.B.5.B.6.(1)x8-y8;(2)-16x2.7.(1)x2y4(xy2+z)(xy2-z);(2)(m-n+4mn)(m-n-4mn);(3)12x(2a-1)2.8.原式=(x+1)(2x-3)x.当x=12时,原式=-32.9.324-1=(312+1)(36+1)(33+1)(33-1)=28×(312+1)(36+1)(33-1).10.原式=12(a-b)2=2.13.1第1课时1.(1)√;(2);(3)√;(4)√;(5).2.△ABC,△BDC,△BEC;△ABE,△DBE.3.14或16. 5.(1)∠A,∠ACD,∠ADC;∠A,∠ACB,∠B;(2)△DAE,△DAC,△BAC;△ADC,△BDC;(3)△BDC;△ACD,△EDC.不是.6.当四点中任意三点不共线时,组成4个三角形;当四点中有三点共线时,组成3个三角形;若该四点共线时,不能组成三角形.第2课时1.3.2.105厘米或200厘米.3.B.4.B.5.9种:4,5,6,7,8,9,10,11,12(单位:厘米).6.4厘米,6厘米.7.8或10.8.8种:1,4,4;2,3,4;2,4,4;2,4,5;3,4,3;3,4,4;3,4,5;3,4,6.第3课时1.ACE,BCD.2.(1)AE,4厘米;(2)DAC,12;(3)AF.3.C.4.C.5.△ABC,△ABD,△ADC,△ABE,△AEC,△ADE.6.相等.∠1=∠DAC=∠DAE=∠2.∠EAF=∠EDF.7.(1)△BCD,△OCD;(2)△ABC,△ABO和△BOC有一条高重合;△BCD,△OCD 和△BOC有一条高重合.第4课时1.70°.2.45°.提示:∠APD=∠A2+∠C2.3.C.4.C.5.(1)125°;(2)35°.6.70°.7.50°.8.(1)105°;(2)115°;(3)90°+12n°.提示:延长BO交AC于D,∠BOC=∠BDC+12∠C=∠A+12∠B+12∠C=90°+12∠A.13.2第1课时1.n-3,n-2.2.5.3.B.4.D.5.五角星.6.8个;△ABC,△ABD,△BCD,△ACD,△OAB,△OAC,△OBD,△OCD.7.6.8.60厘米.第2课时1.1 440°,360°,144°.2.8.3.12,150°.4.C.5.D.7.36°.8.18,130°.13.3第1课时1..2.O,2厘米.3.圆外,圆内,6.4.弦:AB,BC,CD,AD,BD,AC;半圆:ABC,ADC;优弧:BAD,CAD,BAC,ABD,ACB;劣弧:AB,BC,CD,AD,BCD.6.列方程:2π(80+10)8=2π(80+10+x)10,x=22.5(厘米).第2课时1..2.a2(1-π4).3.3.4.一样远.5.6π.第十三章综合练习1.30°,60°.2.95°.3.钝角.4.∠A=40°,∠C=140°.5.20°.6.M在圆内部.7.B.8.D.9.B.10.D.11.36°,72°,72°.12.(1)y=90-x2;(2)y=45;(3)60.13.8,8,11或10,10,7.14.(1)将平面分为5部分:小圆内、小圆上、圆环内、大圆上、大圆外.(2)条件分别是:OP<5,OP=5,5<OP<8,OP=8,OP>8.15.延长AP到BC上点D,利用三角形外角性质,可推出∠APB>∠C.16.3圈.检测站1.5,4.2.10个.3.2,1.4.六.5.B.6.C.7.3个.8.∠ADB=80°,∠DAE=10°.9.(1)∠AEF>∠D>∠A(由外角定理);(2)∠AFD=∠ACD+∠D=∠A+∠B+∠D.综合与实践第1课时1.条件是:多边形每条边都是该多边形与相邻多边形的公共边,每个顶点处各内角之和是360°.2.正六边形.3.B.4.D.6.6,3,3.第2课时1.正三角形2.正方形.3.C.4.D.5.(1)3,2.6.3n,2n+1.14.11.2,5.2.C.3.储蓄所,诊所(6,9),商店(7,3),学校(1,1).4.5排3列.5.23.6.(1)(C,4),(A,4),(0,3),(0,1),(A,0),(C,0),(D,1),(D,3);(2)(E,3)→(G,4)→(H,2)→(F,3)→(G,1)(答案不唯一).14.21.四,5,2.2.x轴或y轴上.3.C.4.D.5.在第二、四象限的角平分线上,如(1,-1).6.(2,0),(7,0);(0,2),(0,4).7.第二象限,(2,0),(-2,1);第一象限,(2,2),(0,3).14.3第1课时1.B(3,3),D(-2,-2).2.C.3.小房子.4.42.5.(32,3),(64,0).第2课时1.(-2,-3),(3,-4),x′=x-2,y′=y-3.2.A.3.A(0,0),B(5,1),C(0,-3),D(-2,-2).4.(1)(0,0),(0,1.5),(3.8,0),(3.8,1.5),( 1.7,0.5);(2)(-3.8,-1.5),(-3.8,0),(0,-1.5),(0,0),(-2.1,-1).5.以(1,1)为原点O′,x′轴∥x轴,y′轴∥y轴,分别以向右、向上为正向,单位长度不变,建立直角坐标系.A,B,C坐标分别是A(-2,1),B(2,-2),C(-1,2).14.41.北偏西45°,1.5.2.A.3.略.4.略.第十四章综合练习1.(9,8).2.一.3.2.4.6.5.D.6.B.7.略.8.二,四,三,一,x轴,y轴.9.(2,6)或(2,-6).10.x轴上,(0,5),(5,0).检测站1.(-2,-2).2.(1)3;(2)-2;(3)四.3.B.5.“国”字.6.P,Q,R分别在长方形内部、边界上、外部.总复习题1.45°.2.∠DCE=∠A.3.12.4.-2 012.5.125°.6.D.7.D.8.A.9.C.10.75°.11.第二象限.12.24.5吨.13.(1)22x-23,21;(2)-2y2+19y,9.14.12.15.y=-12x.16.购一等门票3张、三等门票33张,或购二等门票7张、三等门票29张.提示:分三种情况分别列二元一次方程组,其中购一等门票、二等门票不可行.17.玩具走的是正12边形,共走了12米.总检测站1.44°.2.(1)AB∥DF;(2)ED∥AC;(3)ED∥AC.3.x=2,y=-5.4.a=-73,b=53.5.-y2-7x.6.-7.7.18°.8.C.9.C.10.A.11.B.12.(1)∠DOC=∠B=∠E;(2)不一定;还可能互补.13.4.14.3516x3-418x2-32x-12.15.(a+1)2(a-1)2.*16.7,5,6.17.12边形.18.分两种情况讨论:D点在B,C之间和D点在B,C之外.分别由面积求出高,建立直角坐标系,以垂足为原点,以直线BC为x轴,以高所在直线为y轴.。

9.3 平行线的性质1.如图,直线a和直线b被直线c所截,且a∥b,若∠1=118°,则∠2=_______.2. 在图5-3-10中,a∥b,计算∠1的度数______.3.如图,因为∠B=∠1(已知)所以________∥________(________________________________),又因为AB∥CD(已知),所以∠3=________(________________________________),所以____+∠3=∠4+________________________________,即∠________=∠________.4.下列语句中,不是命题的是()A.两直线平行,同旁内角相等B.直线AB与CD平行吗C.若|a|=|b|,则a2=b2D.中国的首都是北京5.如图,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF等于()A.180°B.270°C.360°D.540°6.命题“邻补角的平分线互相垂直”的题设是_________________________,结论是_________________________.7.如图,已知∠1=∠2,CE∥BF,则AB∥CD吗?为什么?8.如图,已知AB∥CD,EF交AB于E,交CD于F,∠AEF=68°,FG平分∠EFD,KF⊥FG,求∠KFC的度数.9.已知,如图,∠AOB纸片沿CD折叠,若O′C∥BD,那么O′D与AC平行吗?请说明理由.10.光线在不同的介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.11.如图,直线c与直线a、b相交,且a∥b,则下列结论:(1)∠1=∠2,(2)∠1=∠3,(3)∠3=∠2中正确的个数为()A.0B.1C.2D.312. 如图,已知AB∥CD,CE、AE分别平分∠ACD、∠CAB,则∠1+∠2=_____________.参考答案1.62°2.144°3.AD BC 同位角相等,两直线平行 ∠5 两直线平行,内错角相等 ∠2 ∠5 BAD BCD4.B5.C6.两个角是邻补角 两个角的平分线互相垂直7.AB ∥CD .因为CE ∥BF ,所以∠1=∠B (两直线平行,同位角相等),又因为∠1=∠2,所以∠2=∠B ,所以AB ∥CD (内错角相等,两直线平行).8.因为AB ∥CD ,∠AEF=68°,所以∠EFD=∠AEF=68°(两直线平行,内错角相等),又因为FG 平分∠EFD ,所以∠EFG=∠GFD=21∠EFD=34°(角平分线定义), 又因为KF ⊥FG ,所以∠KFG=90°(垂直定义),所以∠KFC=180°-∠GFD-∠KFG=56°9.平行.因为O ′C ∥BD ,所以∠2=∠3(两直线平行,内错角相等),又∠1=∠2,∠3=∠4,所以∠1=∠4,所以AC ∥O ′D(内错角相等,两直线平行).10.∠5=180°-∠2=58°,∠6=∠5=58°,∠4=∠2=122°,∠3=∠1=45°,∠7=180°-∠1=135°,∠8=∠7=135°. 11.D 12.90°初中数学试卷。
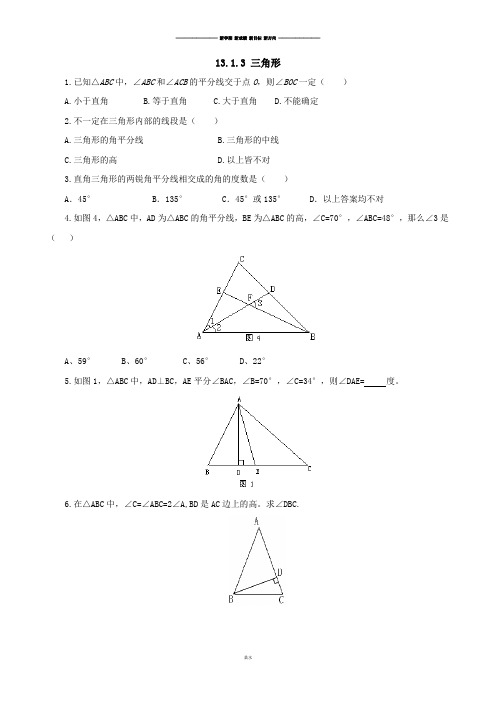
13.1.3 三角形1.已知△ABC中,∠ABC和∠ACB的平分线交于点O,则∠BOC一定()A.小于直角B.等于直角C.大于直角D.不能确定2.不一定在三角形内部的线段是()A.三角形的角平分线B.三角形的中线C.三角形的高D.以上皆不对3.直角三角形的两锐角平分线相交成的角的度数是()A.45° B.135°C.45°或135°D.以上答案均不对4.如图4,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是()A、59°B、60°C、56°D、22°5.如图1,△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,则∠DAE=度。
6.在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高。
求∠DBC.参考答案1.C 解析:因为在△ABC中,∠ABC+∠ACB180°,所以∠BOC90°.故选C.2.C 解析:因为三角形的中线、角平分线都在三角形的内部,而钝角三角形的高有的在三角形的外部,所以答案选C.3.C 解析:∵AE、BD是直角三角形中两锐角平分线,∴∠OAB+∠OBA=90°÷2=45°.两角平分线组成的角有两个:∠BOE与∠EOD,根据三角形外角和定理,∠BOE=∠OAB+∠OBA=45°,∴∠EOD=180°-45°=135°,故选C.4.B5. 186.解:设∠A=X°则∠C=∠ABC=2 X°由三角形内角和定理得∠A+∠ABC+∠C=180°所以有X+2X+2X=180 解得X=36° 所以∠C=72°因为BD是AC边上的高所以∠BDC=90所以∠DBC=90°-∠C=90°-72°=18°初中数学试卷桑水出品。

数学练习册七年级下册参考答案8.11.(1)∠A,∠C;(2)∠ABC,∠ABD,∠DBC,∠ADB,∠BDC;(3)3个,∠ABD,∠ABC,∠DBC.2.B.3.(1)∠AEB,∠DAE,∠BEC,∠ADB;(2)∠C,∠D.4.3个角;6个角;10个角.5.9时12分或21时12分.8.21.(1)42°;(2)不变.2.C.3.D.5.46°.提示:设∠COE=x°,则x-8=130-2x,x=46.6.(1)45°;(2)不变;提示:90+2x2-x=45;(3)不变.提示:90-2y2+y=45.8.3第1课时1.(1)42°20′24″;(2)56.35.2.(1)61°38′10″;(2)32.6.3.C.4.C.5.(1)93°12′;(2)47°31′48″;(3)12°9′36″;(4)33°7′12″.6.(1)112°27′;(2)51°55′;(3)125°37′30″.7.0.5°,6°.8.(1)15°;(2)172.5°.9.40分钟.第2课时1.153°.2.53°17′45″.3.C.4.C.5.63°.6.(1)相等;(2)180°.7.60°.8.41.∠3,∠AOD.2.121°.3.C.4.B.5.∠3=25°30′,∠2=45°.6.∠2=63°30′,∠3=53°.7.(1)2对;(2)6对;(3)12对.8.51.70°.2.45°.3.D.4.C.5.132°.6.135°.7.60°,30°.第八章综合练习1.130°.2.36°16′30″.3.50°.4.(1)54°34′,125°26′;(2)α-90°.5.47.6.D.7.A.8.C.9.D.10.138°.11.125°.12.∠AOC+∠BOC=2(∠DOC+∠COE)=2×90°=180°,A,O,B共线.13.设∠BOE=x°,∠EOC=2x°,∠AOB=180-3x,∠DOB=72-x.得方程(72-x)×2=180-3x,解得x=36.即∠EOC=72°.14.∠BOC+∠COD+∠AOD=270°,∠EOF=170°,∠AOE+∠BOF=190°-90°=100°.∠COF+∠DOE=100°.又∠EOF=170°,∠COD=170°-100°=70°.检测站1.45°.2.98.505°.3.∠AOB,∠BOC.∠AOB,∠BOD.4.C.5.D.6.∠BOD,∠FOE,∠BOC;∠BOF.7.45°.8.97.5°.9.11.∠END.2.DE,AB,BC;AB,BC,DE.3.B.4.C.5.∠CAD,∠BAC,∠B.6.同位角:∠EAD与∠B;∠EAC与∠B;内错角:∠DAC 与∠C;∠EAC与∠C.同旁内角:∠DAB与∠B;∠BAC与∠B.7.略.9.21.相交,平行.2.不相交.3.一.4.C.5.略.6.略.7.正方形.8.略.9.31.65°,两直线平行,同位角相等,65°,对顶角相等.2.65°.3.B.4.C.5.130°.6.∠B,∠EFC,∠ADE.7.40°.9.4第1课时1.AC,BD,内错角相等,两直线平行.2.(1)EN,BD;(2)AB,CD.3.B.4.∠5=∠2=105°,∠5+∠1=180°.5.DE∥MN.由AB∥MN,DE∥AB.6.提示:由AD∥BC,得∠A+∠B=180°,∠C+∠B=180°,AB∥CD.7.(1)由∠3=∠B,知FD∥AB,知∠4=∠A;(2)由ED∥AC,知∠1=∠C,∠BED=∠A.第2课时1.4厘米.2.BD,BE.3.D.4.由∠B=∠C,知AB∥CD,故∠A=∠D.5.∠1=∠GMC=90°-∠2.6.(1)∠MDF=∠MBE,BE∥DF;(2)不是;它是AB和CD之间的距离.7.在∠B内画射线BF∥AE,则BF∥CD.∠ABF=120°,∠FBC=30°,∠C=180°-30°=150°. 第九章综合练习1.110°.2.AD∥BE,BD∥CE,AD∥BE.3.35°.提示:过点M画MN⊥AB,MN∥EG,∠HMN=∠E,∠HMN=90°-∠AMH.4.C.5.C.6.D.7.126°.8.∠1=115°.9.25°.10.∠3=80°,∠4=100°.11.因为AB∥CD,所以∠AEF=∠2,∠AEG=∠3,因为∠AEG=∠1+∠2,所以∠3=∠1+∠2.12.22°.提示:过点A画直线c∥a.检测站1.内错,同旁内,同位.2.180°.3.A.4.B.5.AB∥CD,AD∥BC.6.AD∥BC.DB平分∠ADC代替第二个条件.10.12.5.3.C4.D.6.a=7,b=-9.7.设需要汽车x辆,共有y人外出参观,35x+15=y,45(x-1)=y.解得x=6,y=225..8.不是.10.2第1课时1.-35x+85,-53y+83.2.x-1=0.3.B.4.(1)x=-12,y=52;(2)s=-3,t=-3;(3)m=2,n=1.5.x=1,y=-1.6.提示:按丙的方法,35x=3,25y=4,得x=5,y=10.第2课时1.2.2.-11.3.C.4.B.5.(1)x=-1,y=-8;(2)x=5,y=272.6.令x+y=a,x-y=b,解得a=2,b=-1,又解得x=12,y=32.7.k=4.10.3第1课时1.4x+y=6,-5x+4y=-7.2.C.3.(1)x=1,y=1,z=1;(2)x=1,y=2,z=3.4.解三元一次方程组,用a 表示解,得x=a,y=a+1,z=a-1,代入方程-x+2y+3z=6,得a=74.5.将z看做已知数,将x,y解出来.得x=1911-z,y=211-z.x+y+2z=1911-z+211-z+2z=2111.第2课时1.加减,①,②.2.B.3.(1)x=2,y=1,z=-1;(2)x=1,y=2,z=2.4.a=1,b=-1,c=1.10.4第1课时1.7x+3=y,8x-5=y.2.320,180.3.C.4.216,1095.90元,100元.6.5元,3元.7.提示:设小长方形宽x,长y,则5x=3y,y+2x=2y+2,得x=6,y=10.第2课时1.112x=0.5+112y,0.5x=(0.5+1)y.2.30,18.3.D.4.C.5.21张铁皮做盒身,28张铁皮做盒盖.6.长木6.5尺,绳长11尺.7.(1)x+y=90,46%x+70%y=90×64%,x=22.5,y=67.5.(2)46%x+70%y=64%(x+y),x∶y=1∶3.*第3课时1.x+y+z=21,x+y-z=5,x-(z-y)=5.2.4,8,10.3.C.4.2,3,5.5.12,8,7.第十章综合练习1.43.2.-1.3.-112,5,(113,0).4.-14.5.x=1,y=2.6.y=23x-53.7.B.8.A.*9.D.10.(1)x=1,z=2;(2)x=6,y=24;(3)x=3,y=2;*(4)x=2,y=-3,z=-1.11.300棵,200棵.12.50人,220件.13.23.14.中型15辆,小型35辆.15.m=-275.16.30千米,70千米,42千米.17.平均每天1只大牛需用饲料20千克,小牛需用5千克.所以王大伯对大牛食量的估计是正确的,对小牛食量的估计偏高.18.火车速度22米/秒,列车长276米.19.(1)x=2,y=2,也是剩下一个方程的解.(2)不唯一.如x-y=0.检测站1.-10.2.a=2,b=1.3.5千克,2千克.4.C.5.C.6.a=5.*7.x=1,y=2,z=3.8.牛值金2两,羊值金1两.9.男生270名,女生260名.11.11.108.2.x12.3.x4.4.D.5.A.6.1.5×108.7.(1)m9;(2)3×1011.8.(1)(a-b)5;(2)-(2x-3y)3n+1.9.0.10.0.11.2第1课时1.-8t3.2.116a4b4.3.-6x2.4.A.5.C.6.(1)28x3y3;(2)anbn;(3)-9a3x3.7.a2b.8.1.9.1102n.10.14位数.第2课时1.(1)x10;(2)-8x12.2.C.3.D.5.(1)19x2y4;(2)215;(3)x12;(4)64m12n6.6.(1)x6n+2;(2)-(a+b)7;(3)35n-2.7.提示:24<33,(24)25<(33)25.11.3第1课时1.12xy3.2.-6x2y3.3.B.4.D.5.(1)m5n2;(2)1.2×1020.6.(1)-14x5y4z2;(2)64x6.7.-730(a-b)8n-4.8.C.第2课时1.3x2-5x3.2.x2-y2.3.D.4.C.5.(1)-3x2y+2xy2-52xy;(2)x4+4x2+2x-4;(3)12b3-b2+6b.6.2m3n3-8m2n3.7.x=-12.8.10.11.4第1课时1.x2-7x+10.2.-6x2-xy+2y2.3.B.4.B.5.(1)-6m2+19m-15;(2)-12x3+14x2-4x; (3)-3y2-23y+108.6.4x2-100x+600.7.-x2-29x+32,1854.8.提示:该代数式的值恒为22.9.x=-110.b=12.第2课时1.x3+2x2-5x-6.2.2a3+5a2+a-3.3.B.4.C.5.(1)m3+2m2-1;(2)2a3-5a2b+8ab2-3b3;(3)-2x3-x2-7x+10.6.x3+x-5,值为-7.7.x=-12.8.0.11.51.4.2.m8.3.xn.4.D.5.B.6.16.7.(1)-a;(2)a3.8.(1)y-x;(2)(x+2y)6.9.2xy.11.6第1课时1.1.2.1.3.0.4.C.5.D.6.(1)64;(2)a.7.(1)3 129;(2)200.8.7.9.a≠0,m=n.第2课时1.181.2.-164.3.100.4.B.5.C.6.(1)200;(2)10099;(3)100.7.10-1,10-2,10-3,10-4.8.a<b<d<c.9.x≠-13.10.1.第3课时1.1.2.1a4.3.a8.4.C.5.125.6.(1)10;(2)x5;(3)11 000 000;(4)1a7.7.13a.8.2-101.第4课时1.1.2×10-4.2.0.000 002 76.3.2.5×10-9.4.D.5.D.6.(1)1.5×10-2;(2)2.1×103;(3)1.5×10-3.7.x=-7.8.1.572×104.9.花粉直径较大,是兔毛直径的7.2倍.第十一章综合练习1.106.2.x9.3.a.4.tn.5.(a+b)2.6.x5.7.a7.8.15x3y3z.9.2a3+2a2b+2ab.10.-2x2+3x-1.11.B.12.B.13.B.14.A.15.(1)x9;(2)-(a+b)4;(3)-a2b2+6ab+23a;(4)-6n+2;(5)2a3+8ab2-14a2b;(6)(2)5x-1,101.17.x=-1.18.(8)-x13y12.16.(1)-x,1;(7)6x2-13xy;-3x2-23x+108;(1)x=4;(2)n=2,m=4;(3)M=x2-6x+9.19.2ab+2b2.20.n(n+5)-(n-3)(n+2)=6(n+1).检测站1.(x+y)5.2.-6a3b3c.3.-2x3-4x2+2x.4.a6b6.5.C.6.B.7.B.8.1.24×10-6.9.299.10.(1)36x2-114x+90;(2)91x2-277x+210.11.长8、宽5.12.11.b2-9a2.2.x4-4.3.1681m2n2-49.4.5x+3y.5.C.6.B.7.(1)c2-9a2b2;(2)9y2-4x4;(3)a4-b4;(4)-5x2-9.8.(1)(300+3)(300-3 )=90 000-9=89 991;(2)1.9.(2n-1)(2n+1)=(2n)2-1.10.原式×3-23-2=332-232.12.2第1课时1.-2ab.2.a2+4ab+4b2.3.k=8.4.B.5.C.6.A.7.(1)9m2-32n+116;(2)x4-2x2+1; (3)a2+2ab+b2;(4)916s2+st+49t2.8.(a+b)2=4ab+(a-b)2.9.a2+2ab+b2=9,a2-2ab+b2=49.ab=14(9-49)=-10.a2+b2=9-2ab=29.第2课时1.4ab.2.a2+b2+c2+2ab-2ac-2bc.3.x2-y2+z2+2xz.4.B.5.B.6.A.7.(1)2a2b2-b4;(2)2y2+2x+5;(3)(100-3)(100-1)(100+1)(100+3)=(104-9)(104-1)=108-105+9=9 9 900 009.8.12.9.48π(a+1).10.8.12.31.2x2y.2.2a4-ab+6.3.a-b-2.4.D.5.C.6.(1)xy(x-y);(2)4ab(bc+4);(3)-2xy(1+ 2x-4x2);(4)-(3a+b)(a+3b);(5)2x(x-y)2(1-2x).7.1999.8.14ax(2a-x)2.9.能.256-510=512-510=510(25-1)=24×510.12.4第1课时1.(x+2y)(x-2y).2.k=-140.3.D.4.C.5.(1)(6+x)(6-x);(2)(12y+1)2;(3)-(m-n)2;(4)(3+14a)(3-14a).6.(1)8 056;(2)90 000.7.(1)(1+a+b)(1-a-b);(2)(a-b+2)2.8.左端=[(a-b)2+(a+b)2+(a-b)2-(a+b)2]·[(a-b)2+(a+b)2-(a-b)2+(a+b)2]=4(a-b)2(a+b)2.第2课时1.提出公因式,用公式法进行因式分解.2.x(x+1)(x-1).3.(a-1)(x+y)(x-y).4.D.5.C.6.(1)m(m2+1)(m+1)(m-1).(2)2x3(3y+1)(3y-1).(3)(x+2)2(x-2)2.(4)(x+1)4.7.原式=12·32·23·43·34·54…910·1110=1120.8.2 0122(2 0112-1)+(2 0132-1)=2 0122(2 011+1)(2 011-1)+(2 013+1)(2 013-1)=2 01224 024=1 006.第十二章综合练习1.9x2-y2.2.25-4b2.3.25a2-20ab+4b2.4.14m4+2m2n+4n2.5.-2m.6.x-y+2.7.(xy+2z)(xy-2z).8.23m-0.1n.9.C.10.C.11.C.12.(1)4x2+4xy+y2-25z2;(2)-280y2+1295;(3)116x4-181y4.13.(1)2a3x2(2+a)(2-a);(2)(x-y)(a+2y)(a-2y);(3)-(a-b )2(a+b)2;(4)(x2+2x+7)(x-1)2.14.(1)31×(573+427)×(573-427)=4 526 000;(2)76 900;(3)10099.15.πR2-4πr2=π(R+2r)(R-2r)=3.14×10×5.6=175.8厘米.16.(n+7)2-(n-5)2=(n+7+n-5)(n+7-n+5)=24(n+1).17.x=141.18.x=2,y=-3,16 .19.(2n+1)2-(2n-1)2=(2n+1+2n-1)(2n+1-2n+1)=8n.检测站1.2b-3a.2.20或-20.3.5-a2.4.B.5.B.6.(1)x8-y8;(2)-16x2.7.(1)x2y4(xy2+z)(xy2-z);(2)(m-n +4mn)(m-n-4mn);(3)12x(2a-1)2.8.原式=(x+1)(2x-3)x.当x=12时,原式=-32.9.324-1=(312+1)(36+1)(33+1)(33-1)=28×(312+1)(36+1)(33-1).10.原式=12(a-b)2=2.13.1第1课时1.(1)√;(2);(3)√;(4)√;(5).2.△ABC,△BDC,△BEC;△ABE,△DBE.3.14或16.5.(1)∠A,∠ACD,∠ADC;∠A,∠ACB,∠B;(2)△DAE,△DAC,△BAC;△ADC,△BDC;(3)△BDC;△ACD,△EDC.不是.6.当四点中任意三点不共线时,组成4个三角形;当四点中有三点共线时,组成3个三角形;若该四点共线时,不能组成三角形.第2课时1.3.2.105厘米或200厘米.3.B.4.B.5.9种:4,5,6,7,8,9,10,11,12(单位:厘米).6.4厘米,6厘米.7.8或10.8.8种:1,4,4;2,3,4;2,4,4;2,4,5;3,4,3;3,4,4;3,4,5;3,4,6.第3课时1.ACE,BCD.2.(1)AE,4厘米;(2)DAC,12;(3)AF.3.C.4.C.5.△ABC,△ABD,△ADC,△ABE,△AEC,△ADE.6.相等.∠1=∠DAC=∠DAE=∠2.∠EAF=∠EDF.7.(1)△BCD,△OCD;(2)△ABC,△ABO和△BOC有一条高重合;△BCD,△OCD和△BOC有一条高重合.第4课时1.70°.2.45°.提示:∠APD=∠A2+∠C2.3.C.4.C.5.(1)125°;(2)35°.6.70°.7.50°.8.(1)105°;(2)115°;(3)90°+12n°.提示:延长BO交AC于D,∠BOC=∠BDC+12∠C=∠A+12∠B+12∠C=90°+12∠A.13.2第1课时1.n-3,n-2.2.5.3.B.4.D.5.五角星.6.8个;△ABC,△ABD,△BCD,△ACD,△OAB,△OAC,△OBD,△OCD.7.6.8.60厘米.第2课时1.1 440°,360°,144°.2.8.3.12,150°.4.C.5.D.7.36°.8.18,130°.13.3第1课时1..2.O,2厘米.3.圆外,圆内,6.4.弦:AB,BC,CD,AD,BD,AC;半圆:ABC,ADC;优弧:BAD,CAD,BAC,ABD,ACB;劣弧:AB,BC,CD,AD,BCD.6.列方程:2π(80+10)8=2π(80+10+x)10,x=22.5(厘米).第2课时1..2.a2(1-π4).3.3.4.一样远.5.6π.第十三章综合练习1.30°,60°.2.95°.3.钝角.4.∠A=40°,∠C=140°.5.20°.6.M在圆内部.7.B.8.D.9.B.10.D.11.36°,72°,72°.12.(1)y=90-x2;(2)y=45;(3)60.13.8,8,11或10,10,7.14.(1)将平面分为5部分:小圆内、小圆上、圆环内、大圆上、大圆外.(2)条件分别是:OP<5,OP=5,5<OP<8,OP=8,OP>8.15.延长AP到BC上点D,利用三角形外角性质,可推出∠APB>∠C.16.3圈.检测站1.5,4.2.10个.3.2,1.4.六.5.B.6.C.7.3个.8.∠ADB=80°,∠DAE=10°.9.(1)∠AEF>∠D>∠A(由外角定理);(2)∠AFD=∠ACD+∠D=∠A+∠B+∠D. 综合与实践第1课时1.条件是:多边形每条边都是该多边形与相邻多边形的公共边,每个顶点处各内角之和是360°.2.正六边形.3.B.4.D.6.6,3,3.第2课时1.正三角形2.正方形.3.C.4.D.5.(1)3,2.6.3n,2n+1.14.11.2,5.2.C.3.储蓄所,诊所(6,9),商店(7,3),学校(1,1).4.5排3列.5.23.6.(1)(C,4),(A,4),(0,3),(0,1),(A,0),(C,0),(D,1),(D,3);(2)(E,3)→(G,4)→(H,2)→(F,3)→(G,1)(答案不唯一).14.21.四,5,2.2.x轴或y轴上.3.C.4.D.5.在第二、四象限的角平分线上,如(1,-1).6.(2,0),(7,0);(0,2),(0,4).7.第二象限,(2,0),(-2,1);第一象限,(2,2),(0,3).14.3第1课时1.B(3,3),D(-2,-2).2.C.3.小房子.4.42.5.(32,3),(64,0).第2课时1.(-2,-3),(3,-4),x′=x-2,y′=y-3.2.A.3.A(0,0),B(5,1),C(0,-3),D(-2,-2).4.(1)(0,0),(0,1.5),(3.8,0),( 3.8,1.5),(1.7,0.5);(2)(-3.8,-1.5),(-3.8,0),(0,-1.5),(0,0),(-2.1,-1).5.以(1,1)为原点O′,x′轴∥x轴,y′轴∥y轴,分别以向右、向上为正向,单位长度不变,建立直角坐标系.A,B,C坐标分别是A(-2,1),B(2,-2),C(-1,2).14.41.北偏西45°,1.5.2.A.3.略.4.略.第十四章综合练习1.(9,8).2.一.3.2.4.6.5.D.6.B.7.略.8.二,四,三,一,x轴,y轴.9.(2,6)或(2,-6).10.x轴上,(0,5),(5,0).检测站1.(-2,-2).2.(1)3;(2)-2;(3)四.3.B.5.“国”字.6.P,Q,R分别在长方形内部、边界上、外部.总复习题1.45°.2.∠DCE=∠A.3.12.4.-2 012.5.125°.6.D.7.D.8.A.9.C.10.75°.11.第二象限.12.24.5吨.13.(1)22x-23,21;(2)-2y2+19y,9.14.12.15.y=-12x.16.购一等门票3张、三等门票33张,或购二等门票7张、三等门票29张.提示:分三种情况分别列二元一次方程组,其中购一等门票、二等门票不可行.17.玩具走的是正12边形,共走了12米.总检测站1.44°.2.(1)AB∥DF;(2)ED∥AC;(3)ED∥AC.3.x=2,y=-5.4.a=-73,b=53.5.-y2-7x.6.-7.7.18°.8.C.9.C.10.A.11.B.12.(1)∠DOC=∠B=∠E;(2)不一定;还可能互补.13.4.14.3516x3-418x2-32x-12.15.(a+1)2(a-1)2.*16.7,5,6.17.12边形.18.分两种情况讨论:D点在B,C之间和D点在B,C之外.分别由面积求出高,建立直角坐标系,以垂足为原点,以直线BC为x轴,以高所在直线为y轴.。

青岛版七年级数学下册第9章平行线同步测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、已知∠α的两边分别平行于∠β的两边.若∠α=60°,则∠β的大小为( )A .30°B .60°C .30°或60°D .60°或120°2、如图,已知点B 、C 、D 在同一直线上,3B ∠=∠,248∠=︒,则1∠=( )A .42°B .45°C .48°D .无法确定3、如图,一束平行光线中,插入一张对边平行的纸版,如果光线与纸版右下方所成的∠1是110°,那么光线与纸版左上方所成的∠2的度数是( )A .110°B .100°C .90°D .70°4、如图,平行线AB ,CD 被直线AE 所截.若∠1=70°,则∠2的度数为( )A .80°B .90°C .100°D .110°5、如图,1∠与2∠是直线AB 和CD 被直线AE 所截形成的( )A .同位角B .内错角C .同旁内角D .不能确定6、如果两个角的一边在同一直线上,另一边互相平行,则这两个角( )A .相等B .互补C .互余D .相等或互补7、如图,在所标识的角中,下列说法不正确的是( )A .1∠和2∠互为补角B .1∠和4∠是同位角C .2∠和4∠是内错角D .2∠和3∠是对顶角8、如图,将木条a ,b 与c 钉在一起,∠1=100°,∠2=60°.要使木条a 与b 平行,木条a 顺时针旋转的度数至少是( )A.10°B.20°C.30°D.40°9、如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E与BF交于点G.已知∠BGD′=26°,则∠α的度数是()A.77°B.64°C.26°D.87°10、在如图中,∠1和∠2不是同位角的是()A.B.C.D.第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,已知1234l l l l,且∠1=48°,则∠2=_____,∠3=_____,∠4=_____.//,//2、如图,直线a b ∥,三角尺(30°,60,90°)如图摆放,若∠1=52°,则∠2的度数为 _____.3、平行公理:经过直线外一点,有且只有_____条直线与已知直线平行.平行公理的推论(平行线的传递性):如果两条直线都与第三条直线平行,那么这两条直线互相_____.几何语言表示:∵a ∥c , c ∥b (已知)∴_____∥_____(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)4、如图,直线m ∥n .若140∠=︒,230∠=︒,则3∠的大小为_____度.5、如果两条直线都与第三条直线平行,那么这两条直线互相__________.几何语言表示:∵a ∥c , c ∥b (已知)∴__________∥__________(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)三、解答题(5小题,每小题10分,共计50分)1、如图,点D ,E 分别在AB 和AC 上,DE BC ∥,30DBE ∠=︒,25EBC ∠=︒,求BDE ∠的度数.2、如图,方格纸中每个小正方形的边长都是1.(1)过点P 分别画PM ∥AC 、PN ∥AB ,PM 与AB 相交于点M ,PN 与AC 相交于点N .(2)求四边形PMAN 的面积.3、【感知】已知:如图①,点E 在AB 上,且CE 平分ACD ∠,12∠=∠.求证:AB CD ∥.将下列证明过程补充完整:证明:∵CE 平分ACD ∠(已知),∴2∠=∠__________(角平分线的定义),∵12∠=∠(已知),∴1∠=∠___________(等量代换),∴AB CD ∥(______________).【探究】已知:如图②,点E 在AB 上,且CE 平分ACD ∠,AB CD ∥.求证:12∠=∠.【应用】如图③,BE 平分DBC ∠,点A 是BD 上一点,过点A 作AE BC ∥交BE 于点E ,:4:5ABC BAE ∠∠=,直接写出E ∠的度数.4、完成下面的证明.如图,AB 和CD 相交于点O ,∠C =∠COA ,∠D =∠BOD .求证:AC ∥BD .证明:∵∠C =∠COA ,∠D =∠BOD ,又∠COA =∠BOD (① )∴∠C =②∴AC ∥BD (③ )5、如图,AB CD ∥,P 为AB ,CD 之间的一点,已知228∠=︒,58BPC ∠=︒,求∠1的度数.-参考答案-一、单选题1、D【解析】【分析】根据题意画图如图(1),根据平行线性质两直线平行,同位角相等,即可得出∠α=∠1=∠β,即可得出答案,如图(2)根据平行线性质,两直线平行,同旁内角互补,∠α+∠2=180°,再根据两直线平行,内错角相等,∠2=∠β,即可得出答案.【详解】解:如图1,∵a∥b,∴∠1=∠α,∵c∥d,∴∠β=∠1=∠α=60°;如图(2),∵a∥b,∴∠α+∠2=180°,∵c ∥d ,∴∠2=∠β,∴∠β+∠α=180°,∵∠α=60°,∴∠β=120°.综上,∠β=60°或120°.故选:D .【点睛】本题主要考查了平行线的性质,熟练掌握相关性质进行计算是解决本题的关键.2、C【解析】【分析】根据3B ∠=∠,可得AB CE ∥,根据平行线的性质,两直线平行,内错角相等可得1∠=248∠=︒【详解】解:∵3B ∠=∠∴AB CE ∥∴1∠=248∠=︒.故选C【点睛】本题考查了平行线的性质与判定求角度,掌握平行线的性质与判定是解题的关键.3、A【解析】【分析】根据AB∥CD,BC∥AD,分别得到∠1+∠ADC=180°,∠2+∠ADC=180°,因此∠1=∠2,即可求解.【详解】解:如图:∵AB∥CD,∴∠1+∠ADC=180°,∵BC∥AD,∴∠2+∠ADC=180°,∴∠1=∠2.∵∠1=110°,∴∠2=110°.故选:A.【点睛】本题考查平行线的性质,两直线平行,同旁内角互补.4、D【解析】【分析】直接利用对顶角以及平行线的性质分析得出答案.【详解】解:∵∠1=70°,∴∠1=∠3=70°,∵AB//DC,∴∠2+∠3=180°,∴∠2=180°−70°=110°.故答案为:D.【点睛】此题主要考查了平行线的性质以及对顶角,正确掌握平行线的性质是解题关键.5、C【解析】【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的内部,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.【详解】解:如图,∠与21∠是直线AB和CD被直线AE所截形成的同旁内角.故选:C.【点睛】本题主要考查了同旁内角的概念,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.6、D【解析】【分析】根据平行线的性质,结合图形解答即可.【详解】如图,当AE∥BD时,∠EAB与∠DBC符合题意,∴∠EAB=∠DBC;如图,当AE∥BD时,∠EAF与∠DBC符合题意,∵∠EAB+∠EAF=180°,∠EAB=∠DBC,∴∠DBC+∠EAF=180°,故选D.【点睛】本题考查了平行线的性质,熟练掌握平行线的性质,灵活运用属性结合是解题的关键.7、C【解析】【分析】根据同位角、内错角、邻补角、对顶角的定义求解判断即可.【详解】解:A、1∠和2∠是邻补角,故此选项不符合题意;B、1∠是同位角,故此选项不符合题意;∠和4C、2∠不是内错角,故此选项符合题意;∠和4∠是对顶角,故此选项不符合题意.D、2∠和3故选:C.【点睛】此题考查了同位角、内错角、对顶角以及邻补角的定义,熟记同位角、内错角、邻补角、对顶角的定义是解题的关键.三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.8、B【解析】【分析】由平行线的性质可求解旋转后的∠1的对顶角为120°,将其与∠1的原角度相比较即可求解.【详解】解:如图,当a b∥时,∠2+∠3=180°∵∠2=60°∴∠3=120°∵∠1=∠3∴∠1=120°∵现在木条a与木条c的夹角∠1=100°∴木条a顺时针旋转的度数至少是120°﹣100°=20°故选:B.【点睛】本题考查了对顶角,平行线的性质.解题的关键在于确定角度之间的数量关系.9、A【解析】【分析】本题首先根据∠BGD′=26°,可以得出∠AEG=∠BGD′=26°,由折叠可知∠α=∠FED,由此即可求出∠α=77°.【详解】解:由图可知:AD∥BC∴∠AEG=∠BGD′=26°,即:∠GED=154°,由折叠可知: ∠α=∠FED,∴∠α=12GED=77°故选:A.【点睛】本题主要考察的是根据平行得性质进行角度的转化.10、D【解析】【分析】同位角的定义:两条直线a,b被第三条直线c所截,在截线c的同侧,被截两直线a,b的同一方向的两个角,我们把这样的两个角称为同位角,依此即可求解.【详解】解:A、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;B、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;C、∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;D、∠1与∠2的一边不在同一条直线上,不是同位角,符合题意.故选:D.【点睛】本题题考查三线八角中的同位角识别,解题关键在于掌握判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.二、填空题1、48° 132° 48°【解析】【分析】根据两直线平行内错角相等可求出∠2,根据两直线平行,同位角相等可求出∠4,同旁内角互补可求出∠3.【详解】解:∵1l //2l ,∠1=48°,∴∠2=∠1=48°,∵3l //4l ,∠1=48°,∴∠4=∠1=48°,∵1l //2l ,∴∠3+∠4=180°∴∠3=180°-∠4=180°-48°=132°故答案为:48°;132°;48°【点睛】此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键.2、38 ##38度【解析】【分析】如图,标注字母,过B 作,BC a ∥ 再证明,BC b ∥证明12,EBD从而可得答案.【详解】解:如图,标注字母,过B 作,BC a ∥1=,EBC,a b ∥,BC b ∥2=,DBC12,EBD∠1=52°,90,EBD ∠=︒2=905238.故答案为:38︒【点睛】本题考查的是平行公理的应用,平行线的性质,掌握“两直线平行,内错角相等”是解本题的关键.3、 一 平行 a b【解析】略4、70【解析】如图(见解析),过点B 作AB m ,再根据平行线的性质可得140,230ABC ABD ∠=∠=︒∠=∠=︒,然后根据角的和差即可得.【详解】解:如图,过点B 作AB m ,140ABC ∴∠=∠=︒,m n ,AB n ∴,230ABD ∴∠=∠=︒,3403070ABC ABD ∴∠=∠+∠=︒+︒=︒,故答案为:70.【点睛】本题考查了平行线的性质与推论,熟练掌握平行线的性质是解题关键.5、 平行 a b【解析】略三、解答题1、125BDE ∠=︒【解析】先求出∠ABC 的度数,再利用平行线的性质求解.【详解】解:∵30DBE ∠=︒,25EBC ∠=︒,∴∠ABC =∠DBE +∠EBC =55°,∵DE ∥BC ,∴∠BDE +∠ABC =180°,∴∠BDE =180°-∠ABC =125°.【点睛】此题考查平行线的性质:两直线平行,同旁内角互补,熟记平行线的性质并掌握图形中各角度之间的位置关系是解题的关键.2、(1)见解析;(2)18.【解析】【分析】(1)直接利用网格结合平行线的判定方法得出答案;(2)利用四边形PMAN 所在矩形减去周围三角形面积得出答案.【详解】解:(1)如图所示:点M ,点N 即为所求;(2)四边形PMAN 的面积为:5×7﹣12×3×3﹣12×2×4﹣12×2×4﹣12×3×3=18.【点睛】本题考查网格与作图—作直线外一点作已知直线的平行线,网格图形面积等知识,是基础考点,掌握相关知识是解题关键.3、【感知】ECD ;ECD ;内错角相等,两直线平行;【探究】见解析;【应用】40°【解析】【分析】感知:读懂每一步证明过程及证明的依据,即可完成解答;探究:利用角平分线的性质得∠2=∠DCE ,由平行线性质可得∠DCE =∠1,等量代换即可解决; 应用:利用角平分线的性质得∠ABE =∠CBE ,由平行线性质可得∠CBE =∠E ,等量代换得∠E =∠ABE ,由:4:5ABC BAE ∠∠=即可求得∠ABC 的度数,从而可求得∠E 的度数.【详解】感知∵CE 平分ACD ∠(已知),∴2=ECD (角平分线的定义),∵12∠=∠(已知),∴1∠=∠ECD (等量代换),∴AB CD ∥(内错角相等,两直线平行).故答案为:ECD ;ECD ;内错角相等,两直线平行探究∵CE 平分ACD ∠,∴2ECD ∠=∠,∵AB CD ∥,∴l ECD ∠=∠,∵12∠=∠.应用∵BE 平分∠DBC , ∴12ABE CBE ABC ∠=∠=∠,∵AE ∥BC ,∴∠CBE =∠E ,∠BAE +∠ABC =180゜,∴∠E =∠ABE ,∵:4:5ABC BAE ∠∠=,∴∠ABC =80゜∴40ABE ∠=︒∴40E ∠=︒【点睛】本题考查平行线的判定与性质,角平分线的性质,掌握平行线的性质与判定是关键.4、①对顶角相等;②D ∠;③内错角相等,两直线平行.【解析】【分析】先根据对顶角相等、等量代换可得C D ∠=∠,再根据平行线的判定即可得证.【详解】证明:∵,C COA D BOD ∠=∠∠=∠,又COA BOD ∠=∠(对顶角相等),∴C ∠=D ∠,∴AC BD (内错角相等,两直线平行),故答案为:①对顶角相等;②D ∠;③内错角相等,两直线平行.【点睛】本题考查了对顶角相等、平行线的判定,熟练掌握平行线的判定方法是解题关键.5、30°【解析】【分析】首先过点P 作射线PN AB ∥,根据两直线平行,内错角相等,即可求得答案.【详解】过点P 作射线PN AB ∥,如图①.∵PN AB ∥,AB CD ∥,∴PN CD ∥.∴4228∠=∠=︒.∵PN AB ∥,∴31∠=∠.又∵34582830BPC ∠=∠∠=︒︒=︒--.∴130∠=︒.【点睛】此题考查了平行线的判定与性质.平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.。
12.1 认识二元一次方程组(B)设计人:张晶审核人:李敏教学寄语:好的开始是成功的一半。
学习目标:1.通过对实际问题的分析,使学生进一步体会方程及方程组是刻画现实世界的有效数学模型。
2.掌握二元一次方程、二元一次方程组及其解得概念,并会判断一个数是不是给出的二元一次方程组的解。
学习重难点:重点:二元一次方程、二元一次方程组及其解的概念。
难点:二元一次方程解的个数。
学习过程:一、导入二、检查预习看本章情景导航中的问题并回答以下问题:1.哪些是已知量那些是未知量?2.有哪些等量关系3.如果设长城东段的长为x,西段的长为y千米,那么长城的全长为,西段比东段长。
4.观察你所列的两个方程,它们是一元一次方程吗?为什么?它们的共同点是什么?5.能否仿照一元一次方程给这样的方程加以命名?总结:像这样,含有两个未知数,并且含未知数的项都是一次的方程,叫做。
三、合作探究:1.以上两个方程中的 xy呢?2.把你所列的两个方程这样,便得到一个二元一次方程组。
3.4.5.二元一次方程和二元一次方程组的解(1)x=1,y=2适合方程x+y=3吗?x=-1,y=4呢?(2)你还能找出其它x,y的值适合方程x+y=3 吗?试一试。
叫做二元一次方程的一个解。
(1) 二元一次方程有多少个解?是不是任意一对有理数都是它的解?举例说明。
(1)的解吗?是方程(2)的解吗?所以 1)(2)的公共解。
总结:二元一次方程组中两个方程的公共解,做 。
四、练一练1.(1)哪几对数值是方程x-3y=3的解?哪几对数值是方程3x-10y=5的解? (2) 哪一对数值是方程组 的解?是二元一次方程组 的解吗?呢?五.典型例题解决课本75页 例题1,并回答下列问题:题目中哪些是已知量?哪些是未知量?有哪些等量关系?六.课堂达标检测 1、已知方程组(1) (2) (3) (4)正确的说法是( )A. 只有(1)(3)是二元一次方程组B. 只有(3)(4)是二元一次方程组C. 只有(1)(4)是二元一次方程组D. 只有(2)是二元一次方程组2.方程x+y=4 和A B C D3.方程x+y=3有( )个解,有( )组正整数解,它们是( )七、课后反思: 八、布置作业课本76页习题12.1A 组第1,2,4题。
16.3实数1.如图,实数﹣3、x 、3、y 在数轴上的对应点分别为M 、N 、P 、Q ,这四个数中绝对值最小的数对应的点是( )A .点MB .点NC .点PD .点Q23 )A .0B .-4C πD 23.下列各数中,比2-大的数是( )A .3-B .92- C .0 D .2-4.若x 37﹣4,则x 的取值范围是( )A .2<x <3B .3<x <4C .4<x <5D .5<x <65132252的结果估计在A .7与8之间B .8与9之间C .9与10之间D .10与11之间6.一个正方形的面积等于30,则它的边长a 满足( )A .4<a <5B .5<a <6C .6<a <7D .7<a <87.比较2537的大小,正确的是( )A .3257<<B .3275<<C 3725<<D 3752<<8.估计48的立方根的大小在( )A .2与3之间B .3与4之间C .4与5之间D .5与6之间9.在下面数据中,无理数是( )A 35B 16C .203 D .0.585858…10.对于有理数x y 、. 规定新运算: *x y ax by =+,其中a b 、是常数,已知()2*152*24=-=,,则12*3=( ).A .1B .2C .3D .411.如图,观察所给算式,找出规律:1+2+1=4,1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,……根据规律计算1+2+3+…+99+100+99+…+3+2+1=____________12.已知m n 的小数部分,则m+n =________.13.已知一个无理数a ,满足1<a<2,则这个无理数a 可以是________(写出一个即可).14.一个四位数,记千位上和百位上的数字之和为x ,十位上和个位上的数字之和为y ,如果x =y ,那么称这个四位数为“和平数”.例如:2635,x =2+6,y =3+5,因为x =y ,所以2635是“和平数”.(1)请判断:3562 (填“是”或“不是”)“和平数”.(2)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;(3)如果一个“和平数”的个位上的数字是千位上的数字的两倍,且百位上的数字与十位上的数字之和是14,求满足条件的所有“和平数”.15.用“※”定义一种新运算:对于任意有理数a 和b ,规定22a b ab ab a =++※.如21313213116=⨯+⨯⨯+=※.(1)求()3-2※的值;(2)若113422a +⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭※※,求a 的值. 16.观察下列等式:第1个等式:1111a 11323==⨯-⨯(); 第2个等式:21111a 35235==⨯-⨯(); 第3个等式:31111a 57257==⨯-⨯();3第4个等式:41111a 79279==⨯-⨯(); … 请解答下列问题:(1)按以上规律列出第5个等式:a 5= = ;(2)用含有n 的代数式表示第n 个等式:a n = = (n 为正整数);(3)求a 1+a 2+a 3+a 4+…+a 100的值.参考答案1.D【解析】∵实数-3,x,3,y在数轴上的对应点分别为M、N、P、Q,∴原点在点M与N之间,∴这四个数中绝对值最大的数对应的点是点Q.故选D.2.C【分析】首先利用估算可知12<<,从而排除A、B选项,然后再就被开方数与C、D选项加以比较,最后得出答案即可.【详解】由题意得:12<<,∴排除A、B选项,∵23π<<<<,>故选:C.【点睛】本题主要考查了实数的大小比较,熟练掌握相关方法是解题关键.3.C【分析】根据实数大小的比较法则:正数大于0,负数小于0,正数大于负数;两个负数,绝对值大的反而小,即可得出答案.【详解】32,->-则32-<-, A错误;92,2->-则922-<-,B错误;20-<,C符合题意;22-=-,故D错误;故选C.【点睛】本题考查实数大小的比较.掌握实数大小比较的方法是解题的关键. 4.A【分析】根据36<37<49,则有6<7,即可得到x的取值范围.【详解】∵36<37<49,<7,﹣4<3,故x的取值范围是2<x<3.故选:A.【点睛】本题考查了估算无理数的大小:利用完全平方数和算术平方根对无理数的大小进行估算.5.A【分析】先根据二次根式的运算法则将算式化简,然后根据算术平方根的意义估值即可.【详解】解:原式4===+,34<<Q,748∴<<,故选:A.【点睛】本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,先进行二次根式的乘除运算,然后合并同类二次根式.6.B【分析】,再由52=25,62=36,即可求解.【详解】正方形的面积是边长的平方,∵面积为30,.∵52=25,62=36,∴56<<,即5<a<6,故选B.5【点睛】本题考查了无理数的估算,解题的关键是注意找出和30最接近的两个能完全开方的数.7.C【分析】先分别求出这三个数的六次方,然后比较它们的六次方的大小,即可比较这三个数的大小.【详解】解:∵26=64,362125⎡⎤==⎢⎥⎣⎦,26349⎡⎤==⎢⎥⎣⎦,而49<64<125∴6662<<2<<故选C .【点睛】此题考查的是无理数的比较大小,根据开方和乘方互为逆运算将无理数化为有理数,然后比较大小是解决此题的关键.8.B【分析】即可得出答案.【详解】4,即48的立方根的大小在3与4之间,故选:B .【点睛】9.A【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【详解】解:是无理数,故本选项符合题意;4=,是整数,属于有理数,故本选项不合题意;C.203是分数,属于有理数,故本选项不合题意;D.0.585858…是循环小数,属于有理数,故本选项不合题意.故选:A.【点睛】此题考查无理数的定义,解题关键在于掌握无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.10.C【分析】已知等式利用题中的新定义化简,计算即可求出所求.【详解】解:根据题中的新定义得:25 224a ba b+=⎧⎨-+=⎩,解得:13 ab=⎧⎨=⎩,原式=2×1+ 13×3=3,故选C.【点睛】本题考查的是解二元一次方程组,先根据题中所给的条件列出关于a、b的二元一次方程组是解答此题的关键.11.10000【解析】观察这几个式子可得每个式子的结果等于中间数的平方,所以1+2+3+…+99+100+99+…+3+2+1=1002=10000.点睛:本题考查了数字规律的计算,解决本题的关键在于根据所给的算式,找到规律,并把规律应用到解题中.712【分析】的大小然后得出m,n的值计算即可.【详解】<<<<解:∵m n的小数部分,且34,34∴m=3,-3.【点睛】本题主要考查的是估算无理数的大小,关键是得到m、n的值.13或或其他正确答案【分析】由于无理数a为无理数,1<a<2,a<<,a之间任意一个无理数,由此即可求解.【详解】解:∵a为无理数,1<a<2a<<或其他正确答案.或其他正确答案.【点睛】此题主要考查了无理数的估算,其中无理数包括开方开不尽的数,和π有关的数,有规律的无限不循环小数.14.(1)是;(2)1001,9999;(3)这个数为2864或4958.【分析】(1)用定义验证x和y是否相等(2)找最小和最大的单位数,注意千位数不能为0(3)根据“和平数”定义,以及个数位之间的关系确定【详解】解:(1)x=3+5=8,y=6+2=8∵x=y∴3562是“和平数”∴答案:是这个(2)最小的自然数为0,最大的单位数为9,但千位数字不能为0∴最小的“和平数”为:1001最大的“和平数”为:9999(3)解:设这个“和平数”为abcd则d=2a,a+b=c+d,b+c=14∴2c+a=14∴a为偶数2,4,6(舍去),8(舍去),d=4,6,12(舍去),14(舍去),①当a=2,d=4时 2c+a=14∴c=6∵b+c=14∴b=8②当a=4,d=8时 2c+a=14∴c=5∵b+c=14∴b=9∴综上所述:这个数为2864或4958【点睛】本题考查给出新定义后,如何用它来解题的方法.15.(1)3;(2)a=1.【分析】(1)利用题中新定义化简,计算即可得到结果;(2)已知等式利用新定义化简,计算即可解出a的值.【详解】解:(1)根据题中定义的新运算得:3)※(-2)=3×(-2)2+2×3×(-2)+3=12-12+3=3.9(2)根据题中定义的新运算得:12a +※3=12a +×32+2×12a +×3+12a +=8(a +1) . 8(a +1) ※(12-)=8(a +1)×21()2-+2×8(a +1)×1()2-+8(a +1)=2(a +1) . 所以2(a +1)=4,解得a =1.【点睛】本题考查了新定义问题,解题的关键是理解题中给出的定义,并运用到具体的计算中.16.(1)1111 9112911⨯-⨯,()(2)()()1111 2n 12n+122n 12n+1⨯--⨯-,()(3)100201【分析】(1)(2)观察知,找等号后面的式子规律是关键:分子不变,为1;分母是两个连续奇数的乘积,它们与式子序号之间的关系为:序号的2倍减1和序号的2倍加1.(3)运用变化规律计算【详解】解:(1)a 5=1111=9112911⨯-⨯(); (2)a n =()()1111=2n 12n+122n 12n+1⨯--⨯-();(3)a 1+a 2+a 3+a 4+…+a 10011111111111=1++++232352572199201⨯-⨯-⨯-⋅⋅⋅⨯-()()()() 11111111111200100=1++++=1==23355719920122012201201⎛⎫⎛⎫⨯---⋅⋅⋅-⨯-⨯ ⎪ ⎪⎝⎭⎝⎭.赠送:七年级上册寒假复习专项训练(三)一、基础过关(22分)1.默写(10分)细读孔子的《论语》,你会体会到一种原创的活力和睿智。
青岛版七年级数学下册第9章平行线同步测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、下列说法正确的是 ( )A .不相交的两条直线是平行线.B .如果线段AB 与线段CD 不相交,那么直线AB 与直线CD 平行.C .同一平面内,不相交的两条射线叫做平行线.D .同一平面内,没有公共点的两条直线是平行线.2、下列说法中正确的有( )(1)两条直线被第三条直线所截,同位角相等;(2)若12390∠+∠+∠=︒,则1∠,2∠,3∠互余;(3)相等的两个角是对顶角;(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.A .0个B .1个C .2个D .3个3、下列说法错误的是( )A .经过两点,有且仅有一条直线B .平面内过一点有且只有一条直线与已知直线垂直C .两点之间的所有连线中,线段最短D .平面内过一点有且只有一条直线与已知直线平行4、一副直角三角板如图放置,点C 在FD 的延长线上,AB ∥CF ,∠F =∠ACB =90°,∠A =60°,则∠DBC 的度数为( )A .45°B .25°C .15°D .20°5、如图,在所标识的角中,下列说法不正确的是( )A .1∠和2∠互为补角B .1∠和4∠是同位角C .2∠和4∠是内错角D .2∠和3∠是对顶角6、如图,直线a 、b 被直线c 所截,下列选项中不一定能判定a ∥b 的是( )A .∠1=∠3B .∠1=∠4C .∠2=∠4D .∠2=∠57、如图,直线l1∥l2,∠1=136°,则∠2的度数是()A.44°B.46°C.54°D.64°8、若∠1与∠2是内错角,则它们之间的关系是()A.∠1=∠2B.∠1>∠2C.∠1<∠2D.∠1=∠2或∠1>∠2或∠1<∠29、如图,木工用图中的角尺画平行线的依据是()A.垂直于同一条直线的两条直线平行B.平行于同一条直线的两条直线平行C.同位角相等,两直线平行D.经过直线外一点,有且只有一条直线与这条直线平行10、如图,四边形中,AD∥BC,AC与BD相交于点O,若S△ABO=5cm2,S△DCO为()A.5cm2B.4cm2C.3cm2D.2cm2第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,小明同学在练习本上的相互平行的横格上先画了直线a,度量出∠1=112°,接着他准备在点A处画直线b.若要使b∥a,则∠2的度数为_____度.2、如图,三条直线两两相交,其中同旁内角共有_______对,同位角共有______对,内错角共有_______对.3、指出图中各对角的位置关系:(1)∠C 和∠D 是_____角;(2)∠B 和∠GEF 是____角;(3)∠A 和∠D 是____角;(4)∠AGE 和∠BGE 是____角;(5)∠CFD 和∠AFB 是____角.4、如图,把一条两边边沿互相平行的纸带折叠,若56β∠=︒,则α∠=_______.5、如图,已知DE ∥BC ,∠ABC =70°,那么直线AB 与直线DE 的夹角等于 ___度.三、解答题(5小题,每小题10分,共计50分)1、如图,方格纸中每个小正方形的边长都是1.(1)过点P分别画PM∥AC、PN∥AB,PM与AB相交于点M,PN与AC相交于点N.(2)求四边形PMAN的面积.2、如图,∠1=70º,∠2 =40º,∠B=70º.(1)求∠C的度数;(2)如果DE平分∠ADC,那么DE与AB平行吗?请说明理由.DE BC交直线3、已知:如图,点D是直线AB上一动点,C是直线外一点.连接CD,过点D作∥AC于点E.(1)如图1,当点D 在线段AB 上时,①依题意,在图1中补全图形;②若100ABC ∠=︒,20BCD ∠=︒,则ADC ∠=______度.(2)当点D 在直线AB 上时,请写出ADC ∠、ABC ∠、BCD ∠的数量关系,请任选一个结论证明.4、如图,这些图案中有一些平行条纹请你设计一些类似图案,并把你的设计与同学们交流一下.5、探究:如图1直线AB 、BC 、AC 两两相交,交点分别为点A 、B 、C ,点D 在线段AB 上过点D 作∥DE BC 交AC 于点E ,过点E 作EF AB ∥交BC 于点F .若50ABC ∠=︒,求∠DEF 的度数. 请将下面的解答过程补充完整,并填空(理由或数学式)解:DE BC ∥,DEF ∴∠=_____________.(_____________) EF AB ∥,∴_________ABC =∠.(_______________)DEF ABC ∴∠=∠.(等量代换)50ABC ∠=︒,DEF ∴∠=___________.应用:如图2,直线AB 、BC 、AC 两两相交,交点分别为点A 、B 、C ,点D 在线段AB 的延长线上,过点D 作∥DE BC 交AC 于点E ,过点E 作EF AB ∥交BC 于点F .若65ABC ∠=︒,求DEF ∠的度数并说明理由-参考答案-一、单选题1、D【解析】【分析】根据平行线的定义逐项分析即可.【详解】A 、同一平面内不相交的两条直线是平行线,故此说法错误;B 、两条线段不相交也可以不平行,故此说法错误;C 、同一平面内,不相交的两条射线可以平行,也可以既不平行也不相交,故此说法错误;D 、同一平面内,没有公共点的两条直线是平行线,此说法正确,故选D .【点睛】本题考查了平行线的定义,理解此定义是关键,属于概念基础题.2、A【解析】【分析】两条平行直线被第三条直线所截时,同位角相等;两个和为90︒的角互为余角;两相交线的对顶角相等;从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离.【详解】(1)两条直线被第三条直线所截,同位角不一定相等,故错误;(2)两个角的和为90︒,这两个角互为余角,故错误;(3)相等的两个角不一定是对顶角,对顶角一定相等,故错误;(4)从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,故错误;故选:A.【点睛】本题考查了同位角,余角,对顶角以及点到直线的距离.解题的关键在于正确理解各名词的定义.3、D【解析】【分析】根据垂线的性质、线段的性质、直线的性质、平行公理判断下列选项.【详解】解:由垂线的性质、线段的性质、直线的性质可知A、B、C正确;A、根据直线的性质可知选项正确,不符合题意;B、根据垂线的性质可知选项正确,不符合题意;C、根据线段的性质可知选项正确,不符合题意;D、由平行公理可知选项不正确,需要保证该点不在已知直线上,符合题意;故选:D.【点睛】本题主要考查了垂线的性质、线段的性质、直线的性质、平行公理,解题的关键是掌握相关的概念.4、C【解析】【分析】直接利用三角板的特点,结合平行线的性质得出∠ABD=45°,进而得出答案.【详解】解:由题意可得:∠EDF=45°,∠ABC=30°,∵AB∥CF,∴∠ABD=∠EDF=45°,∴∠DBC=45°-30°=15°.故选:C.【点睛】此题主要考查了平行线的性质,根据题意得出∠ABD的度数是解题关键.5、C【解析】【分析】根据同位角、内错角、邻补角、对顶角的定义求解判断即可.【详解】解:A、1∠和2∠是邻补角,故此选项不符合题意;B、1∠是同位角,故此选项不符合题意;∠和4C、2∠不是内错角,故此选项符合题意;∠和4∠是对顶角,故此选项不符合题意.D、2∠和3故选:C.【点睛】此题考查了同位角、内错角、对顶角以及邻补角的定义,熟记同位角、内错角、邻补角、对顶角的定义是解题的关键.三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定.在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.6、B【解析】【分析】根据平行线的判定逐项判断即可得.【详解】解:A、13∥,此项不符题意;∠=∠,根据同位角相等,两直线平行能判定a bB、14∥,此项符合题意;∠=∠,不一定能判定a bC、24∠∠∥,此项不符题意;=,根据同位角相等,两直线平行能判定a bD、25∠=∠,根据内错角相等,两直线平行能判定a b∥,此项不符题意;故选:B.【点睛】本题考查了平行线的判定,熟练掌握判定方法是解题关键.7、A【解析】根据两直线平行,同位角相等求出∠1的同位角∠3的度数,再根据邻补角进行求解.【详解】∵直线l1∥l2,∠1=136°,∴∠1=∠3=136°∴∠2=180°-∠3=180°-136°=44°.故选:A.【点睛】本题考查了平行线的性质,熟记性质两直线平行,同位角相等是解题的关键.8、D【解析】【分析】根据内错角角的定义和平行线的性质判断即可.【详解】解:∵只有两直线平行时,内错角才可能相等,∴根据已知∠1与∠2是内错角可以得出∠1=∠2或∠1>∠2或∠1<∠2,三种情况都有可能,【点睛】本题考查了内错角和平行线的性质,能理解内错角的定义是解此题的关键.9、C【解析】【分析】由于角尺是一个直角,木工画线实质是在画一系列的直角,且这些直角有一边在同一直线上,根据平行线的判定即可作出判断.【详解】由于木工画一条线实际上是在画一个直角,且这些直角的一边在同一直线上,且这些直角是同位角相等,因而这些直线平行.故选:C【点睛】本题是平行线判定在实质中的应用,关键能够把实际问题转化为数学问题.10、A【解析】【分析】分别过点A 、D 作AE BC ⊥、DF BC ⊥,根据平行线的性质可得AE DF =,根据三角形的面积求得ABO DCO S S =△△,即可求解.【详解】解:分别过点A 、D 作AE BC ⊥、DF BC ⊥,如下图:∵//AD BC∴AE DF = 又∵12ABC S BC AE =⨯△,12DCB S BC DF =⨯△ ∴ABC DCB S S =△△∵ABO ABC CBO S S S =-△△△,DCO DCB CBO S S S =-△△△∴2=5ABO DCO S S cm =△△故选A【点睛】此题考查了平行线的性质以及三角形的面积公式,解题的关键是根据平行线的性质及三角形的面积公式推出ABO DCO S S =△△.二、填空题1、68【解析】【分析】根据平行线的性质,得出23∠∠=,根据平行线的判定,得出13180∠+∠=︒,即可得到368∠=︒,进而得到2∠的度数.【详解】解:∵练习本的横隔线相互平行,∴23∠∠=,b a,∵要使//∠+∠=︒,∴13180又1112∠=︒,∴368∠=︒,即268∠=︒,故答案为:68.【点睛】本题主要考查了平行线的性质与判定条件,解题时注意:两直线平行,同位角相等;同旁内角互补,两直线平行.2、 6 12 6【解析】【分析】根据同位角、同旁内角和内错角的定义判断即可;【详解】如图所示:同位角有:1∠与5∠;1∠与10∠;2∠与6∠,2∠与9∠;6∠与12∠;3∠与12∠;7∠与11∠;8∠与10∠;8∠与4∠;7∠与3∠;5∠与9∠;4∠和11∠,共有12对;同旁内角有:2∠与5∠;4∠与10∠;7∠与12∠;3∠与8∠;3∠与9∠;8∠与9∠,共有6对; 内错角有:4∠与9∠;3∠与5∠;7∠与9∠;3∠与10∠;8∠与12∠;2∠与8∠,共有6对; 故答案是:6;12;6.【点睛】本题主要考查了同位角、内错角、同旁内角的判断,准确分析判断是解题的关键.3、 同旁内 同位 内错 邻补 对顶【解析】【分析】根据同位角,同旁内角,内错角,邻补角,对顶角的定义进行逐一判断即可.【详解】解:(1)∠C 和∠D 是同旁内角;(2)∠B 和∠GEF 是同位角;(3)∠A 和∠D 是内错角;(4)∠AGE 和∠BGE 是邻补角;(5)∠CFD 和∠AFB 是对顶角;故答案为:(1)同旁内 (2)同位 (3)内错 (4)邻补(5)对顶.【点睛】本题主要考查了同位角,同旁内角,内错角,邻补角,对顶角的定义,解题的关键在于能够熟知定义.4、62°##62度【解析】【分析】如图,根据平行线的性质可得1β∠=∠,根据折叠的性质可得21=α∠+∠∠,再利用平角等于180°,据此求解即可.【详解】解:∵纸片两边平行,∴1=56β∠=∠︒由折叠的性质可知,21=α∠+∠∠, ∴21180α∠+∠=︒,∴α∠=62°.故答案为:62°.【点睛】本题主要考查平行线的性质,折叠的性质,解此题的关键在于熟练掌握其知识点.5、70或110##110或70【解析】【分析】先根据平行线的性质,求得∠AFE的度数,再根据邻补角的定义,即可得到∠AFD的度数.【详解】解:如图,直线AB和DE相交于点F,∵BC∥DE,∠ABC=70°,∴∠AFE=∠ABC=70°,∠AFD=180°-∠AFE=110°,∴直线AB、DE的夹角是70°或110°.故答案为:70或110.【点睛】本题主要考查了平行线的性质,熟记“两直线平行,同位角相等”是解题的关键.三、解答题1、(1)见解析;(2)18.【解析】【分析】(1)直接利用网格结合平行线的判定方法得出答案;(2)利用四边形PMAN所在矩形减去周围三角形面积得出答案.【详解】解:(1)如图所示:点M ,点N 即为所求;(2)四边形PMAN 的面积为:5×7﹣12×3×3﹣12×2×4﹣12×2×4﹣12×3×3=18.【点睛】本题考查网格与作图—作直线外一点作已知直线的平行线,网格图形面积等知识,是基础考点,掌握相关知识是解题关键.2、(1)见解析;(2)平行,见解析【解析】【分析】(1)由1B ∠=∠可得AD ∥BC ,进而根据平行线的性质即可求得∠C 的度数;(2)根据∠2 =40º,以及DE 平分∠ADC ,求得701ADE ∠=︒=∠,根据内错角相等两直线平行即可证明DE ∥AB .【详解】(1)∵∠1=70°∠B =70°∴∠1=∠B∴AD ∥BC∴∠C =∠2=40°(2)如果DE 平分∠ADC ,则AB ∥DE理由:∵DE 平分∠ADC ,∠2 =40º∴∠ADE =∠CDE =18022︒-∠=180402︒-︒=70° 又∵∠1=70°∴∠ADE =∠1=70°∴DE ∥AB .【点睛】本题考查了平行线的性质与判定,角平分线的定义,掌握平行线的性质与判定是解题的关键.3、 (1)①见解析;②120(2)∠ADC =∠ADE +∠EDC 或∠ADC =∠ABC −∠BCD 或∠ABC +∠ADC +∠BCD =180°,证明见解析【解析】【分析】(1)①依题意补全图形即可;②由平行线的性质及已知,可得∠ADE 、∠EDC 的度数,由∠ADC =∠ADE +∠EDC 即可求得结果;(2)分D 点在线段AB 上、D 点在AB 的延长线上、D 点在BA 的延长线上三种情况考虑,根据平行线的性质即可求得ADC ∠、ABC ∠、BCD ∠的数量关系.(1)①补全的图形如图1,②//DE BC ,∴100ADE ABC ∠=∠=︒,∠EDC =∠BCD =20°,∴∠ADC =∠ADE +∠EDC =100°+20°=120°;故答案为120;(2)当D 点在线段AB 上时,如图1,∠ADC =∠ADE +∠EDC理由如下://DE BC ,∴ADE ABC =∠∠,∠EDC =∠BCD ,∴∠ADC =∠ADE +∠EDC ;当D 点在AB 的延长线上时,如图2,∠ADC =∠ABC −∠BCD ;理由如下://DE BC ,∴ADE ABC =∠∠,∠EDC =∠BCD ,∴∠ADC=∠ADE−∠EDC=∠ABC−∠BCD;当D点在BA的延长线上时,如图3,∠ABC+∠ADC+∠BCD=180°;理由如下:DE BC,//∴∠ADE=∠ABC,∠BCD+∠EDC=180°,∴∠ADE+∠ADC+∠BCD=180°,∴∠ABC+∠ADC+∠BCD=180°.【点睛】本题考查了平行线的性质,角的和差运算,涉及分类讨论,掌握平行线的性质是关键,注意分类讨论.4、答案见解析(答案不唯一)【解析】【分析】只要设计的图案中有平行线即可,答案不唯一.【详解】解:如下图:【点睛】本题考查的是带有平行条纹的图案设计,根据平行的定义画图是解题关键.5、探究:∠EFC ;两直线平行,内错角相等;∠EFC ;两直线平行,同位角相等;50°;应用:115︒,见解析.【解析】【分析】探究:根据平行线的性质填写证明过程即可;应用:根据探究的方法利用平行线的性质求角度即可.【详解】探究:DE BC ∥,DEF ∴∠=EFC ∠.(_两直线平行,内错角相等) EF AB ∥,∴EFC ∠ABC =∠.(两直线平行,同位角相等_)DEF ABC ∴∠=∠.(等量代换)50ABC ∠=︒,DEF ∴∠=50︒.应用:DE BC ∥,∴∠ABC =∠ADE =65°.(两直线平行,同位角相等)∵EF ∥AB ,∴∠ADE +∠DEF =180°.(两直线平行,同旁内角互补)∴∠DEF =180°−65°=115°.【点睛】本题考查了平行线的性质求角度,掌握平行线的性质是解题的关键.。
13.1.1 三角形
1.以下列各组线段长为边,能组成三角形的是()
A.1 cm,2 cm,4 cm B.8 cm,6 cm,4 cm
C.12 cm,5 cm,6 cm D.2 cm,3 cm ,6 cm
2.等腰三角形的两边长分别为5 cm和10 cm,则此三角形的周长是()
A.15 cm B.20 cm C.25 cm D.20 cm或25 cm
3.下列说法中正确的是()
A.三角形可分为斜三角形、直角三角形和锐角三角形
B.等腰三角形任何一个内角都有可能是钝角或直角
C.三角形外角一定是钝角
D.在△ABC中,如果∠AB∠C,那么∠A60°,∠C60°
4.下列各组线段,能组成三角形的是()
A、2 cm,3 cm,5 cm
B、5 cm,6 cm,10 cm
C、1 cm,1 cm,3 cm
D、3 cm,4 cm,8 cm
5.在下列条件中:①∠A+∠B=∠C;②∠A:∠B∠:∠C=1:2:3;③∠A=90°-∠B;④∠A=∠B=∠C,能确定△ABC是直角三角形的条件有()个.
A.1
B.2
C.3
D.4
6.已知等腰三角形两边长是4cm和9cm,则它的周长是。
参考答案
1.B
2.C
3.D
4.B
5.C
6.22cm 初中数学试卷。