异方差的检验与修正

一、异方差问题检验与修正
1、使用双对数模型
Ln Y = β0+β1 ln X1 + β2 ln X2 + μ
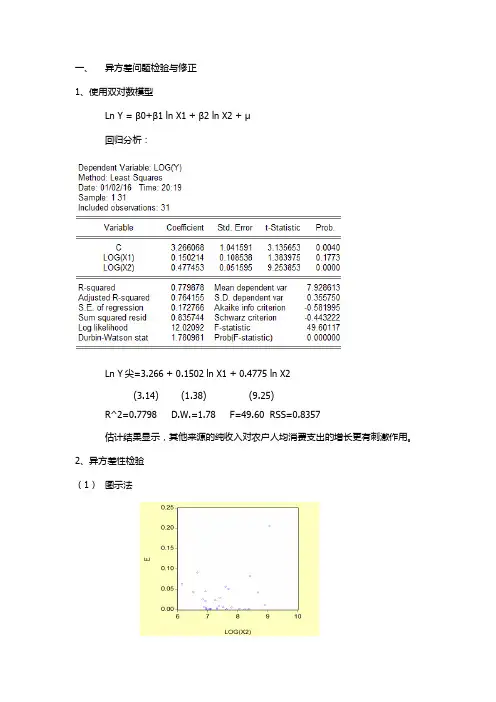
回归分析：
Ln Y尖=3.266 + 0.1502 ln X1 + 0.4775 ln X2
(3.14) (1.38) (9.25)
R^2=0.7798 D.W.=1.78 F=49.60 RSS=0.8357
估计结果显示，其他来源的纯收入对农户人均消费支出的增长更有刺激作用。

2、异方差性检验
（1）图示法
Log（E）=-6.010808+0.451832 log（lx2）
(-0.679156) (0.102484)
可以看出，有91%的概率认为 X2的参数为0.451832是显著的，因此X2存在异方差性。

可知 X2可能存在异方差性。

（4）怀特（White）检验
从图中可得，X2项的参数的t检验是显著的且怀特统计量n R^2=31*0.7648=23.70
因此，X2具有异方差性
3、异方差的修正
根据帕克检验算权重：w=1/残差
Log（E）=-6.010808+0.451832 log（lx2）
(-0.679156) (0.102484)
W=1/(lx2^0.6721845)
可以看出，对原模型进行加权最小二乘估计得到
Ln y尖=3.005048+ 0.201401 ln X1 + 0.463065 ln X2 修正前 R^2=0.775025
修正后R^2=0.999999。

stata异方差检验和解决命令在数据分析中，异方差是一个常见的问题。

异方差指不同样本的方差不相等，这会导致统计结果的不准确性。

Stata提供了许多方法来检验和解决异方差问题。

一、异方差检验检验异方差通常使用Breusch-Pagan-Godfrey(BPG)检验或White检验。

这里以BPG检验为例，该检验的原假设是方差相等，备择假设是方差不相等。

命令格式：estat hettest示例代码：reg y x1 x2 x3estat hettest如果p值小于0.05，则拒绝原假设，说明存在异方差问题。

二、异方差稳健标准误当检测到异方差问题时，可以使用异方差稳健标准误来解决。

异方差稳健标准误在计算系数的标准误时考虑了异方差问题，从而提高了结果的准确性。

命令格式：robust示例代码：reg y x1 x2 x3, robust使用robust命令后，结果中的Standard Error一栏即为异方差稳健标准误。

三、异方差稳健回归如果异方差问题比较严重，只使用异方差稳健标准误可能无法解决问题。

此时可以使用异方差稳健回归。

命令格式：robust示例代码：reg y x1 x2 x3, vce(robust)使用vce(robust)参数后，回归结果中的系数和标准误都是异方差稳健的，并且t值和p值也已经经过了调整。

总结：通过Breusch-Pagan-Godfrey检验或White检验可以检验异方差问题，如果存在异方差问题，可以使用异方差稳健标准误或异方差稳健回归来解决。

在使用robust命令时，不需要进行任何假设检验，因为参数已经考虑了异方差问题。

第1篇一、实验目的1. 掌握异方差性的基本概念和检验方法。

2. 学会运用统计软件进行异方差的检验和修正。

3. 提高对计量经济学模型中异方差性处理能力的实践应用。

二、实验原理1. 异方差性：在回归分析中，若回归模型的误差项（残差）的方差随着自变量或因变量的取值而变化，则称模型存在异方差性。

2. 异方差性的检验方法：图形检验、统计检验（如F检验、Breusch-Pagan检验、White检验等）。

3. 异方差性的修正方法：加权最小二乘法（WLS）、广义最小二乘法（GLS）等。

三、实验步骤1. 数据准备1. 收集实验所需数据，确保数据质量和完整性。

2. 对数据进行初步处理，如剔除异常值、缺失值等。

2. 模型设定1. 根据研究问题，选择合适的回归模型。

2. 利用统计软件（如Eviews、Stata等）进行初步的回归分析。

3. 异方差性检验1. 图形检验：绘制散点图，观察残差与自变量或因变量的关系，初步判断是否存在异方差性。

2. 统计检验：- F检验：检验回归系数的显著性。

- Breusch-Pagan检验：检验残差平方和与自变量或因变量的关系。

- White检验：检验残差平方和与自变量或因变量的多项式关系。

4. 异方差性修正1. 若检验结果表明存在异方差性，则需对模型进行修正。

2. 选择合适的修正方法：- 加权最小二乘法（WLS）：根据残差平方与自变量或因变量的关系，计算权重，加权最小二乘法进行回归分析。

- 广义最小二乘法（GLS）：根据残差平方与自变量或因变量的关系，选择合适的方差结构，广义最小二乘法进行回归分析。

5. 结果分析1. 对修正后的模型进行回归分析，观察回归系数的显著性、拟合优度等指标。

2. 对实验结果进行分析，解释实验现象，验证研究假设。

6. 实验报告撰写1. 撰写实验报告，包括以下内容：- 实验目的- 实验原理- 实验步骤- 实验结果- 分析与讨论- 结论2. 实验报告应结构清晰、逻辑严谨、语言简洁。

异方差的诊断与修正心得体会关键词，样品重复测定法;独立样本检验;抽样误差;样本均数比。

异方差的基础研究现状(一)异方差概念异方差是指总体均数与样本均数之间的差异。

异方差分析就是在控制其他变量不受影响的情况下，通过分析两个或几个独立的样本均数之间的差异来揭示和确认样本内部所存在的系统性偏差的方法。

(二)异方差产生原因1.由于随机误差造成的系统性偏差。

如果两次测定结果都落入同一区域，则称为等位变动。

若两次测定值大小无明显差别，但方向相反，这种情形叫做等方变动。

若两次测定值虽然大小接近，但方向相反，且各自占据了相邻的两个区域，我们把它们称作等距变动。

2.由于实验者主观上的疏忽造成的系统性偏差。

如果某些测定项目中含有未知参数，那么在第三次测定时，人为地加入该参数并将其置零后再读取数据，此时很容易发生系统性偏差。

一、样本量较小的单因素实验设计优点：1.可以在控制其他条件的前提下进行单因子处理2.只有当被试出现负偏离时才需要考虑是否存在异方差问题3.相对于多因素而言，其精度低4.当样本含量增加到一定程度时，异方差问题更加突出5.当样本含量减少时，由于抽样误差的影响，使实验结果波动范围扩大6.为多元回归分析创造条件7.适用于连续测定8.测定次数越多，信息量越丰富缺点：1.需要的样本量较大2.样本含量高时，实验结果的波动幅度也大3.难以排除样本的偶然性干扰4.需要的样本量太大5.费时、费力，不经济。

二、独立样本检验独立样本检验(independent sample test)又称为相互独立性检验。

它是指两组测定值之间是否存在异方差，应先假定两组测定值是完全相互独立的，即如果两组测定值是完全独立的，则说明两组测定值之间没有异方差存在，否则，说明两组测定值之间存在着异方差。

(一)独立样本检验的基本思想1.样本方差不变，只根据样本均数的差异，推论两个独立样本均数之间的差异。

2.样本方差变化，仅根据样本均数的差异，推论两个独立样本均数之间的差异。

实验报告课程名称：实验项目名称：单方程线性回归模型中异方差的检验与补救院（系）：专业班级：姓名：学号：实验地点：实验日期：年月日实验目的：掌握利用EViews软件对模型中存在的异方差进行检验和补救。

实验内容：根据我国2000年部分地区城镇居民每个家庭平均全年可支配收入X与消费支出Y 的统计数据，通过建立双变量线性回归模型分析人均可支配收入对人均消费支出的线性影响，并讨论异方差的检验与修正过程。

1、异方差的检验1）图示法2）Park检验3）Glejser检验4）Goldfeld-Quandt检验5）White检验2、异方差的补救1）加权最小二乘法（WLS）2）对数变换实验方法、步骤和结果：一、建立工作文件并完成数据输入1、File---new---workfile2、Quick---Empty Group ----paste3、将ser01重命名为x，ser01重命名为y二、写模型的估计方程Quick---Estimate Equation---y c x，得到在不考虑异方差且其他假定都成立的情况下的估计结果，如下图所示：三、异方差的检验找y的估计值在估计结果中点击forcast 将其重命名为yf生成残差序列：在估计窗口中点击proc---make residual series将resid01重命名为res，并保存（一）图示法（对异方差粗略的判定）1.用x-y的散点图进行判断，看是否存在明显的散点扩大、缩小或是复杂性的变动趋势X y ----open----as GroupView---graph ----scatter-----simple scatter2、用y的估计值与残差平方的散点图进行判断，看是否存在一条斜率为零的直线Quick---graph----scatter—写入方程yf res^2图形显示斜率不为零，所以可知模型存在异方差3、任一解释变量x与残差平方的散点图进行判断，看是否存在一条斜率为零的直线Quick—graph—scatter写入方程x res^2图形显示斜率不为零，所以可知模型存在异方差由以上三种图示法可知，模型存在异方差（二）帕克（Park）检验（将图示法公式化）Quick—Estimate Equation---log(res^2) c log(x)由估计结果可知：log（x）=3.703235 P=0.020622<0.05，所以拒绝原假设，模型具有统计显著性，即模型具有异方差。

White检验修正异方差权重选择引言在统计学中，方差是一个重要的概念，用于衡量数据的离散程度。

在许多实际问题中，我们经常会遇到异方差（heteroscedasticity）的情况，即数据的方差不是恒定的。

异方差可能会导致统计推断的失准，因此需要进行异方差的检验和修正。

White检验和修正是一种常见的统计方法，用于检验和修正异方差对统计推断的影响。

本文将详细讨论White检验的原理和方法，并介绍异方差权重的选择方法。

White检验什么是White检验White检验，也称为异方差鲁棒检验（heteroscedasticity-robust test），是一种用于检验回归模型中异方差是否存在的统计检验。

它是基于普通最小二乘法（OLS）估计的残差，并通过估计残差的方差函数来进行检验。

White检验的原理White检验的基本原理是比较OLS估计的标准误差与异方差-稳健（heteroscedasticity-robust）标准误差之间的差异。

如果存在异方差，则两者会有明显的差别。

White检验的零假设是不存在异方差，备择假设是存在异方差。

White检验的步骤White检验的步骤如下：1.根据回归模型的残差计算残差的平方，并与自变量的值相乘得到异方差的函数形式。

2.运用一阶条件等式，将该异方差函数形式引入对数似然方程，进行最大似然估计。

3.比较OLS估计的标准误差与基于最大似然估计的异方差-稳健标准误差之间的差异。

4.使用相应的统计检验进行检验，判断是否存在异方差。

White检验的应用White检验广泛应用于经济学、金融学、社会科学等领域的回归分析中。

它可以帮助研究人员验证回归模型中是否存在异方差，并提供修正方法，提高统计推断的准确性。

White修正异方差权重选择异方差修正权重的选择方法在进行White修正时，需要选择适当的异方差修正权重。

常见的异方差权重选择方法包括以下几种：1.白噪声检验：通过计算OLS残差的平方并与自变量相乘，运用相应的统计检验对异方差进行检验，并根据检验结果选择权重。

异方差性的概念类型后果检验及其修正方法异方差性（heteroscedasticity）是指随着自变量的变化，被解释变量的方差不保持恒定，呈现出不同的分散特征。

异方差性可能会导致线性回归模型的参数估计不精确，误差项的标准误差的估计不准确，常见的检验和修正方法包括Breusch-Pagan检验和White检验，同时，还可以采取加权最小二乘法或者转换变量的方法来修正异方差性。

异方差性可以分为条件异方差和非条件异方差两种类型。

条件异方差是指在给定自变量的情况下，被解释变量方差的大小存在差异；非条件异方差则是指被解释变量的方差在整个样本空间内都存在差异。

异方差性的后果是导致参数估计的不准确性和偏误。

当存在异方差性时，OLS（普通最小二乘法）估计的标准误差会低估真实标准误差，从而使得参数显著性以及模型拟合效果可能出现问题。

此外，在存在异方差性的情况下，t检验、F检验等假设检验的结果也会受到影响。

在进行线性回归模型时，常常需要对异方差性进行检验。

一种常用的检验方法是Breusch-Pagan检验，其基本思想是对残差的平方与自变量进行回归，然后通过F检验来判断异方差的存在与否。

另一种常用的检验方法是White检验，它是在一个包含自变量和交互项的扩展模型中对残差的平方与自变量进行回归，通过Wald检验统计量来判断异方差的存在与否。

异方差性可以通过多种修正方法来处理。

其中，一种常用的方法是采用加权最小二乘法（WLS）来估计参数。

WLS的基本思想是将方差不恒定的观测值加权，使得每个观测值的权重与方差的倒数成正比。

另一种常用的方法是通过转换变量，使得原始数据变换成具有恒定方差的形式，例如对数变换、平方根变换等。

下面以一个案例来说明如何检验和修正异方差性。

假设我们研究了城市的房价（被解释变量）与房屋面积和所在地区（自变量）之间的关系。

我们采集了100个样本数据，并构建了线性回归模型进行分析。

1.检验异方差性：使用Breusch-Pagan检验来检验模型的异方差性。

Z N UE L异方差性的检验方法和修正一、 实验目的熟练掌握异方差性的检验方法和修正处理方法二、实验原理异方差（heteroskedasiticity ）是计量经济工作红线性回归模型经常遇到的问题，异方差的存在对线性回归分析有很强的破坏作用。

利用异方差的图形检验、戈德菲尔特-夸特检验、怀特检验方法，检验案例中线性回归模型的异方差是否存在，若存在的话，如何通过加权最小二乘法进行修正，建立能够真正反应案例的经济模型，实现对经济的正确指导作用。

三、实验要求通过Eviews 软件应用给定的案例做异方差模型的图形检验法、Glodfeld-Quanadt（戈德菲尔特-夸特）检验与White（怀特）检验，并使用加权最小二乘法（WLS）对异方差进行修正。

四、 实验步骤在现实经济活动中，最小二乘法的基本假定并非都能满足，本案例讲讨论随机误差项违背基本假定的一个方面—异方差性。

本案例将介绍：异方差模型的图形检验、戈德菲尔特-夸特检验、怀特检验；异方差模型的加权最小二乘法修正。

1、建立workfile 和对象，录入2007年城镇居民收入X 和消费额Y 的数据。

2、参数估计按住ctrl 键，同时选中序列X 和序列Y ，点右键，在所出现的右键菜单中，选择open\as Group 弹出一对话框，点击其上的“确定”，可生成并打开一个群对象。

在群对象窗口工具栏中点击view\Graph\Scatter\Simple Scatter, 可得X 与Y 的简单散点图，可以看出X 与Y 是带有截距的近似线性关系。

点击朱界面菜单Quick\Estimate Equation, 在弹出的对话框中输入 Y C X,点确定即可到回归结果，如下：VariableCoefficientStd. Errort-StatisticProb. C 756.6871570.1912 1.3270760.1948X0.3076930.01908216.124970.0000R-squared0.899659 Mean dependent var 8689.161Durbin-Watson stat1.694571 Prob(F-statistic)0.0000003、异方差检验本案例用的是2007年的全国各个诚实城镇居民收入和消费额，由于地区之间这种差异使得模型很容易产生异方差，从而影响模型的估计和运行，为此必须对该模型是否存在异方差进行检验。

【stata代码模板】异方差检验与校正_scatter_imtest_hettest_robust经典线性回归模型的一个重要假定是：总体回归函数中的随机误差项满足同方差。

如果不满足，最小二乘估计虽然是无偏、一致的，但不是有效的，这时采用t检验和f检验则有可能导致错误的结论。

异方差产生可能的原因有：模型中缺少某些变量、测量误差、模型设置不正确、异常值出现。

异方差的形式有几种：残差随着变量增大而增大；残差随着变量增大而减少；与变量的变化呈复杂形式。

1．异方差检验（1）图示法检验简易代码方差为随机变量的离散程度，通过观察y和x的相关图，可以观察的离散程度和解释变量之间的相关关系。

若随x的增加，y的离散程度呈逐渐增加或减少的趋势则表明模型存在着递增或者递减的异方差性。

——————————————模板————————————quietly regress 被解释变量解释变量若干predict yhatpredict e1,residualsrvfplotscatter e1 解释变量——————————————模板————————————Quietly regress语句先建立回归方程，不显示结果。

Predict yhat计算预测值yhat。

predict e1,residuals计算残差值e1rvfplot则是制作残差e1与拟合值yhat之间的散点图，与scatter e1 yhat等价scatter e1 解释变量，是制作残差e1与解释变量1之间的散点图。

（2）怀特检验简易代码原假设是具有同方差，即不存在异方差——————————模板——————————quietly regress 被解释变量解释变量若干estat imtest,white——————————模板——————————（3）B-P检验简易代码原假设是同方差，即不存在异方差——————————模板——————————quietly regress 被解释变量解释变量若干estat hettest 辅助变量若干,rhs 假定选项——————————模板——————————Estat语句中的辅助变量若干，是用来指定辅助回归变量，缺少辅助回归变量则用被解释变量建立辅助回归，如果用rhs则以原模型的解释变量进行辅助回归。

检验异方差性与调整异方差性1. 异方差性的概念及检验方法异方差性指的是随机变量的条件方差，并且条件方差不是常数。

也就是说，观测值的方差不仅仅取决于均值，还可能取决于其他因素。

在统计分析中，如果存在异方差性，会对参数估计和假设检验产生影响。

因此，需要在进行统计分析之前，先检验数据是否存在异方差性。

1.1 异方差性检验方法常用的异方差性检验方法有多种，包括：•基于残差的图形检验方法，如残差图和方差-均值图；•基于统计检验的方法，如Levene检验、Bartlett检验以及Brown-Forsythe检验；1.2 基于残差的图形检验方法1.2.1 残差图残差图是一种简单直观的检验异方差性的方法。

在残差图中，横轴表示预测值或观测值的均值，纵轴表示对应的残差。

如果残差的方差与均值无关，则残差图应该呈现出随机分布的特点。

反之，如果残差图中存在明显的模式，即残差的方差与均值相关，则可以初步判断存在异方差性。

1.2.2 方差-均值图方差-均值图是一种更细致的检验异方差性的方法。

在方差-均值图中，横轴表示预测值或观测值的均值，纵轴表示对应的残差的方差。

如果方差-均值图中存在明显的模式，即残差的方差与均值相关，则可以初步判断存在异方差性。

1.3 基于统计检验的方法1.3.1 Levene检验Levene检验是一种常用的检验异方差性的方法。

Levene检验基于修正后的中位数差异进行计算，主要用于检验两个或多个样本之间的方差是否存在显著差异。

在假设检验中，原假设为各组样本方差相等，备择假设为各组样本方差不等。

如果p值小于设定的显著性水平（如0.05），就可以拒绝原假设，认为样本之间存在异方差性。

1.3.2 Bartlett检验Bartlett检验是另一种常用的检验异方差性的方法。

Bartlett检验基于观测值与各组均值差异进行计算，主要用于检验两个或多个样本之间的方差是否存在显著差异。

在假设检验中，原假设为各组样本方差相等，备择假设为各组样本方差不等。

实验一异方差的检验与修正一、实验目的：了解异方差(heteroscedasticity)、Goldfeld-Quandt检验、Spearman rank correlation 检验、Park检验、Glejser检验、Breusch-Pagan检验、White检验、加权最小二乘法（weighted least squares,简记WLS）、模型对数变换法等基本概念及异方差产生的原因和后果。

掌握异方差的检验与修正方法以及如何运用Eviews软件在实证研究中实现相关检验与修正。

二、基本概念：异方差(heteroscedasticy)就是对同方差假设(assumption of homoscedasticity)的违反。

经典回归中同方差是指随着样本观察点X的变化，线性模型中随机误差项的方差并不改变，保持为常数。

异方差的检验有图示法及解析法，检验异方差的解析方法的共同思想是，由于不同的观察值随机误差项具有不同的方差，因此检验异方差的主要问题是判断随机误差项的方差与解释变量之间的相关性。

异方差的修正方法有加权最小二乘法和模型对数变换法等，其基本思路是变异方差为同方差，或者尽量缓解方差变异的程度。

三、实验内容及要求：内容：根据北京市1978-1998年人均储蓄与人均收入的数据资料，若假定X为人均收入（元），Y为人均储蓄（元），通过建立一元线性回归模型分析人均储蓄受人均收入的线性影响，并讨论异方差的检验与修正过程。

要求：（1）深刻理解上述基本概念（2）思考：异方差的各种检验方法所适用的情况及如何运用加权最小二乘法（WLS）修正异方差？（3）熟练掌握相关Eviews操作四、实验指导：1.用OLS估计法估计参数（1）导入数据打开Eviews软件，选择“File”菜单中的“New--Workfile”选项，出现“Workfile Range”对话框，在“Workfile frequency”框中选择“Annual”,在“Start date”和“End date”框中分别输入“1978”和“1998”，如下图：图1—1 建立新文件然后单击“OK ”，弹出如下窗口：图1—2 建立新文件选择“File ”菜单中的“Import--Read Text-Lotus-Excel ”选项，找到要导入的名为EX3.2.xls 的Excel 文档，单击“打开”出现“Excel Spreadsheet Import ”对话框并在其中输入“x ”和“y ”,如下图所示：图1—3 导入数据再单击“OK ”完成数据导入。

实验1 回归模型的OLS估计及异方差的检验与修正实验内容及要求：表1列出了2000年中国部分省市城镇居民每个家庭平均全年可支配收入x与消费性支出y的统计数据。

（1）利用OLS法建立人均消费支出与可支配收入的线性模型。

（2）检验模型是否存在异方差。

（3）如果存在异方差，试采用适当的方法加以消除。

表1 2000年中国部分省市城镇居民人均可支配收入与消费性支出(单位：元)实验如下：1、通过Y-X的散点图判断，并不存在异方差。

回归结果分析：图1人均消费支出与可支配收入的线性模型：Y =272.3635 + 0.755125Xt =(1.705713) (32.38690)R2=0.983129 D.W.=1.301563 F=1048.912残差分析：图2显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。

2，Goldfeld-Quandt检验⑴将样本安解释变量排序（SORT X）并分成两部分（分别有 1 到8共8个样本合13 到20 共8个样本）⑵利用样本1 建立回归模型1（回归结果如图3），其残差平方和为126528.3Smpl 1 8LS Y C X图3⑶利用样本2 建立回归模型2（回归结果如图4），其残差平方和为615472.0。

图4⑷计算F 统计量：RSS2/RSS1＝615472.0/126528.3=4.864，RSS2、RSS1分别是模型1 和模型2 的残差平方和。

取α=0.05时，查F分布表得F0.05(8-1-1,8-1-1)=4.28，而实际上F=4.864>F0.05=4.28 ，所以存在异方差。

3，White检验⑴建立回归模型：LS Y C X，回归结果如图5图5⑵在方程窗口上点击White Heteroskedastcity,检验结果如图6。

图6由图6中的数据，得到e2=-180998.9+49.42846X-0.002115X2t=(-1.751858) (1.708006) (-1.144742)R2=0.632606White统计量2200.63260612.65212nR=⨯=，该值大于5%显著性水平下自由度为2的2χ分布的相应临界值20.05(2) 5.99χ=，(在估计模型中含有两个解释变量，所以自由度为2)因此拒绝同方差性的原假设。

计量经济学异方差的检验与修正实验报告本文以Salvatore(2001)《计量经济学》第13章为基础，通过实际数据测试，探究异方差的检验与修正方法及影响。

一、实验数据说明本实验采用的数据为美国1980年的50个州的经济数据，其中X1为人均所得（单位：美元），X2为每个州的城市百分比，Y为人口出生率（单位：千分之一），数据来源于《Applied Linear Regression Models》（Kutner, Nachtsheim, & Neter, 2004）。

二、实验原理当数据呈现异方差性时，传统的OLS估计方法将会失效，此时需要使用其他的估计方法。

其中常用的是加权最小二乘（WLS）估计方法。

WLS估计方法的思想是对存在异方差（方差不相等）的观测值进行权重调整，使得加权后的平方残差最小。

本实验将通过检验异方差条件、使用原有OLS估计进行对比以及应用WLS修正方法的实现来说明异方差对实证分析的影响。

三、实验内容及结果首先，为了检验异方差条件是否成立，可以采用Breusch-Pagan检验。

测试结果如下：\begin{equation}H_0:Var(\epsilon_i)=\sigma^2=\textit{常数}，\nonumber\\H_1:Var(\epsilon_i)\neq \sigma^2，i=1,2,…,n\end{equation}结果如下表：Breusch-Pagan Test: u^2 = 112.208 Prob > chi2 = 0.0000通过检验结果可知，Breusch-Pagan检验统计量的p值为0.0000，小于0.05的水平，因此拒绝原假设，认为方差存在异方差。

接下来，我们将使用传统的OLS估计方法进行回归分析（OLS 1），并与WLS估计方法（WLS 1）进行对比。

OLS 1结果如下：\begin{equation}Y=0.0514X1+1.0871X2-58.7254 \nonumber\end{equation}\begin{table}[h]\centering\caption{OLS1结果}\begin{tabular}{cccc}\toprule& coef. & std. err. & t \\\midruleconst & -58.7254 & 23.703 & -2.477 \\X1 & 0.0514 & 0.027 & 1.895 \\X2 & 1.0871 & 0.402 & 2.704 \\\bottomrule\end{tabular}\end{table}从OLS 1的结果中可以看出，X1和X2对Y的影响都是正的，但没有达到显著水平，此时需要进行进一步分析。

实验三异方差的检验与修正实验目的1、理解异方差的含义、后果2、学会异方差的检验与加权最小二乘法实验内容一、准备工作。

建立工作文件，并输入数据，用普通最小二乘法估计方程（操作步骤与方法同前），得到残差序列。

表2列出了1998年我国主要制造工业销售收入与销售利润的统计资料，请利用统计软件Eviews建立我国制造业利润函数模型。

表2 我国制造工业1998年销售利润与销售收入情况二、异方差的检验1、图形分析检验⑴观察销售利润（Y）与销售收入（X）的相关图(图3-1)：SCAT X Y图3-1 我国制造工业销售利润与销售收入相关图从图中可以看出，随着销售收入的增加，销售利润的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

⑵残差分析首先将数据排序（命令格式为：SORT 解释变量），然后建立回归方程。

在方程窗口中点击Resids按钮就可以得到模型的残差分布图（或建立方程后在Eviews工作文件窗口中点击resid对象来观察）。

图3-2 我国制造业销售利润回归模型残差分布图3-2显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。

2、Goldfeld-Quant检验⑴将样本安解释变量排序（SORT X）并分成两部分（分别有1到10共11个样本合19到28共10个样本）⑵利用样本1建立回归模型1（回归结果如图3-3），其残差平方和为2579.587。

SMPL 1 10LS Y C X图3-3 样本1回归结果⑶利用样本2建立回归模型2（回归结果如图3-4），其残差平方和为63769.67。

SMPL 19 28 LS Y C X图3-4 样本2回归结果⑷计算F 统计量：12/RSS RSS F =＝63769.67/2579.59=24.72，21RSS RSS 和分别是模型1和模型2的残差平方和。

取05.0=α时，查F 分布表得44.3)1110,1110(05.0=----F ，而44.372.2405.0=>=F F ，所以存在异方差性 3、White 检验(1)建立回归模型：LS Y C X ，回归结果如图3-5。