结构力学第五章-2(单位荷载法)
- 格式:ppt
- 大小:756.50 KB
- 文档页数:22

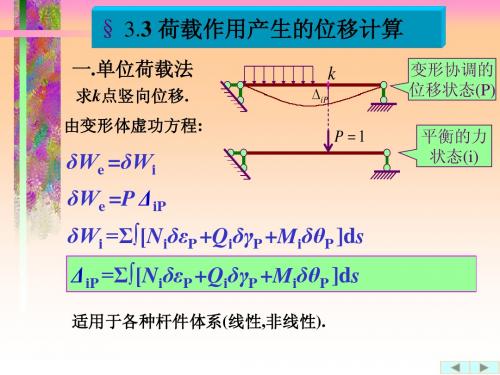
单位荷载法求位移
单位荷载法是一种常用的结构力学分析方法,其主要应用于线性问题的求解。
其中,
通过对结构物的单位荷载进行分析,可以求解出不同点的位移变化情况,从而得到结构物
在受荷状况下的静力响应。
在使用单位荷载法求位移时,通常需要依次进行以下步骤:
一、选择荷载和受力节点
首先需要根据实际问题,选择合适的荷载和受力节点。
荷载可以是均匀荷载、集中荷载、温度荷载等,受力节点可以是结构物的端点或任意位置点。
二、计算屈曲力
通过受力节点引入单位荷载,并在结构物中构造支点反力,可以得到结构物的受力系统。
在此基础上,通过力的平衡条件,计算出结构物在单位荷载下的屈曲力。
三、求解位移
在计算屈曲力之后,可以得到结构物在受荷状况下的弹性位移。
具体而言,根据杨氏
模量、惯性矩等条件,可以利用弹性力学基本方程求解出位移的表达式。
四、对位移进行叠加
在得到单个节点的位移表达式之后,需要对其进行叠加,得到整个结构物在受荷状况
下的位移变化情况。
具体而言,可以通过矩阵运算将所有节点的位移表达式进行叠加计算,得到结构物的位移变形图。
需要注意的是,在使用单位荷载法求解位移时,应当考虑荷载的类型、节点的位置、
结构物的性质等因素对位移计算的影响。
同时,还需要注意数值计算的精度和有效位数等
问题,以保证计算结果的准确性和可靠性。

单位荷载法公式单位荷载法是结构力学中求解结构位移的一种重要方法。
咱们先来说说啥是单位荷载法。
想象一下,有一座桥,咱们想知道桥在某种外力作用下会产生多大的变形或者位移。
这时候单位荷载法就派上用场啦!单位荷载法的核心公式是:$\Delta = \int \overline{M}M_{P}ds/EI$ 。
这里面的 $\Delta$ 表示所求的位移,$\overline{M}$ 是单位荷载作用下结构内力,$M_{P}$ 是原荷载作用下结构内力,$ds$ 表示微段长度,$EI$ 则是结构的抗弯刚度。
为了让大家更清楚单位荷载法的厉害之处,我给大家讲讲我曾经遇到的一个事儿。
有一次,我带着学生们去参观一个正在建设的大楼工地。
工地上的工程师给我们介绍了他们在计算大楼某个部位位移时遇到的难题。
正好,我就给学生们现场讲解了单位荷载法的应用。
当时,我们站在大楼的框架结构旁边,看着那些密密麻麻的钢梁和钢柱。
工程师说,他们需要知道在某一侧增加了一些临时的施工荷载后,大楼的某个关键节点会产生多大的水平位移。
我就引导学生们一起思考,如果我们把这个实际的荷载情况转化为单位荷载作用下的内力和原荷载作用下的内力,然后利用单位荷载法的公式,是不是就能计算出位移啦?学生们一开始有点迷糊,但是在我逐步的引导和解释下,慢慢开始明白了。
我们一起在纸上画出结构的简图,分析受力情况,确定单位荷载的施加位置和方向。
然后计算出单位荷载作用下的弯矩图$\overline{M}$ ,再根据实际的施工荷载计算出原荷载作用下的弯矩图$M_{P}$ 。
接下来就是代入公式进行积分计算啦。
在这个过程中,有的同学计算出错,有的同学对弯矩图的绘制不太准确。
但是大家相互讨论,互相纠正错误,最终算出了大致的位移值。
虽然这个结果可能和工程师们用专业软件计算出来的有一些小的偏差,但是对于学生们来说,这是一次非常宝贵的实践经验。
通过这次实地的观察和计算,学生们深刻地理解了单位荷载法不是书本上枯燥的公式,而是能真正解决实际工程问题的有力工具。



第一章结构的几何构造分析1 •瞬变体系:本来是几何可变,经微小位移后,又成为几何不变的体系,成为瞬变体系。
瞬变体系至少有一个多余约束。
2.两根链杆只有同时连接两个相同的刚片,才能看成是瞬较。
3.关于无穷远处的瞬较:(1)每个方向都有且只有一个无穷远点,(即该方向各平行线的交点),不同方向有不同的无穷远点。
(2)各个方向的无穷远点都在同一条直线上(广义)。
(3)有限点都不在无穷线上。
4.结构及和分析中的灵活处理:(1)去支座去二元体。
体系与大地通过三个约束相连时,应去支座去二元体;体系与大地相连的约束多于4个时,考虑将大地视为一个刚片。
(2)需要时,链杆可以看成刚片,刚片也可以看成链杆,且一种形状的刚片可以转化成另一种形状的刚片。
5.关于计算自由度:(基本不会考)(1),则体系中缺乏必要约束,是几何常变的。
(2)若,则体系具有保证几何不变所需的最少约束,若体系无多余约束,则为几何不变,若有多余约束,则为几何可变。
(3),则体系具有多与约束。
是保证体系为几何不变的必要条件,而非充分条件。
若分析的体系没有与基础相连,应将计算出的W减去3.第二章静定结构的受力分析1.静定结构的一般性质:(1)静定结构是无多余约束的几何不变体系,用静力平衡条件可以唯一的求得全部内力和反力。
(2)静定结构只在荷载作用下产生内力,其他因素作用时,只引起位移和变形。
(3)静定结构的内力与杆件的刚度无关。
(4)在荷载作用下,如果仅靠静定结构的某一局部就可以与荷载维持平衡,则只有这部分受力,其余部分不受力。
(5)当静定结构的一个内部几何不变部分上的荷载或构造做等效变换时,其余部分的内力不变。
(6)静定结构有弹性支座或弹性结点时,内力与刚性支座或刚性节点时一样。
解放思想:计算内力和位移时,任何因素都可以分别作用,分别求解,再线性叠加,以将复杂问题拆解为简单情况处理。
2.叠加院里的应用条件是:用于静定结构内力计算时应满足小变形,用于位移计算和超静定结构的内力计算时材料还应服从胡克定律,即材料是线弹性的。