下载文档原格式
莫尔积分法计算公式推导莫尔积分法的公式推导。
莫尔积分法是一种常见的数值积分方法，它通过将被积函数展开为一组基函数的线性组合，然后利用基函数的正交性质来进行积分计算。
在本文中，我们将详细推导莫尔积分法的公式，以便更好地理解这一数值积分方法的原理和应用。
1. 基函数展开。
首先，我们假设被积函数f(x)可以展开为一组基函数φi(x)的线性组合，即。
f(x) = Σi=1n ciφi(x)。
其中ci为展开系数，φi(x)为基函数。
我们要求基函数φi(x)在积分区间[a, b]上是正交的，即。
∫a^b φi(x)φj(x) dx = 0, i ≠ j。
这样，我们就可以利用基函数的正交性质来简化积分计算。
2. 莫尔积分公式。
根据莫尔积分法的原理，我们可以将被积函数f(x)在积分区间[a, b]上进行展开，得到。
f(x) = Σi=1n ciφi(x)。
然后，我们将被积函数f(x)乘以基函数φj(x)，并在积分区间[a, b]上进行积分，得到。
∫a^b f(x)φj(x) dx = Σi=1n ci∫a^b φi(x)φj(x) dx。
由于基函数φi(x)在积分区间[a, b]上是正交的，即∫a^b φi(x)φj(x) dx = 0, i ≠j，因此上式右边的求和只有在i = j时才会有非零项，即。
∫a^b f(x)φj(x) dx = cj∫a^b φj(x)φj(x) dx。
这样，我们就得到了莫尔积分法的公式：cj = ∫a^b f(x)φj(x) dx / ∫a^b φj(x)φj(x) dx。
3. 数值计算。
莫尔积分法的公式可以用于数值计算被积函数f(x)在积分区间[a, b]上的积分值。
具体地，我们可以选择一组合适的基函数φi(x)，计算出展开系数ci，然后利用展开系数ci和基函数φi(x)的正交性质来进行积分计算。
常见的基函数包括Legendre多项式、Chebyshev多项式、Hermite多项式等，它们在不同的积分区间和被积函数下有不同的适用性。
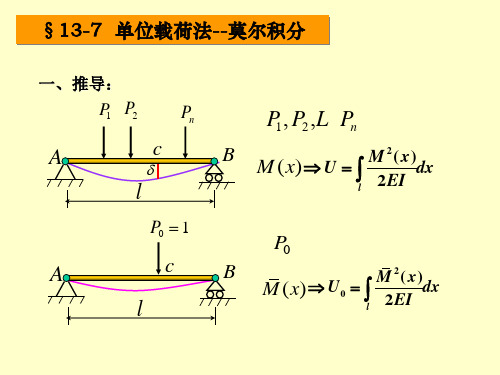
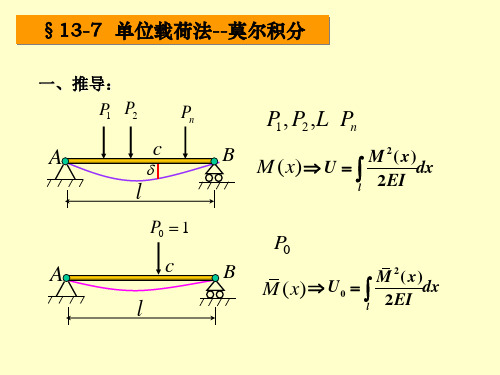
服从胡克定律，有dxV EI x) (轴向拉压扭转22C P =311)P 2ni ii δ==∑对于线弹性体，比例加载的情况是正确的。
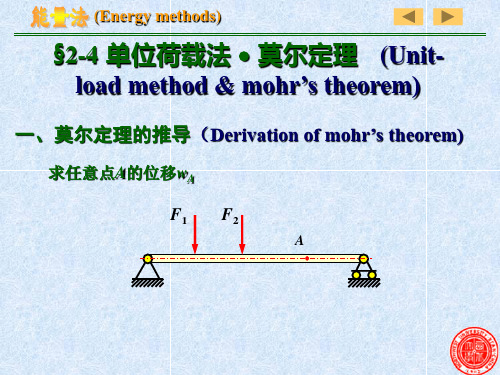
弹性体力学的普遍定理之一。
对于线弹性体，第一力系在第二力系所引起的相应位移上所做的功，等于第二力系在第一力系引起的相应位移上的所作的功。
)n 3）互等定理也是弹性体力学的普遍kkCF V ∆=∂∂克劳迪—恩格赛定理将弹性体的余应变能V C 表示为广义力{F}的函数时，余应变能V C 对任一广义力F k 的偏导数等于该力作用点处、沿力方向的位移Δk 。
kkF V ∆=∂∂ε卡氏第二定理将线弹性体的应变能V Ɛ表示为广义力{F}的函数时，应变能V Ɛ对任一广义力F k 的偏导数等于该力作用点处、沿力方向的位移Δk 。
例14－4 图示刚架ABC ，AB 、BC 各段的弯曲刚度均为EI ，试求自由端A 处承受铅垂集中力P 作用时，A 端截面的转角θ。
BAP aaC例14－12 悬壁梁受分布力q 作用，求B 点挠度。
ABql例14－11 刚架两杆抗弯刚度为EI ，试求C 点水平位移ΔHC 。
BAPba C参考书1.S.T. Timoshenko, James.M. Gere (Stanford University), “Mechanics ofMaterials”,Van Nostrand Reinhold Company Ltd., London.1972, 1984, 1990, 1997, 20012.孙训方《材料力学》（四版），高等教育出版社，2002年。
3.[美]R.C.Hibbeler, 汪越胜译，《材料力学》2003，电子工业出版社，20064.苏翼林《材料力学》（二版，上、下册），高等教育出版社，1987年。
三版，天津大学出版社，2001年5月。
5.刘鸿文《材料力学》（四版），高等教育出版社，2003年。
6.清华大学《材料力学习题集》北京：人民教育出版社，1978年。
