单位载荷法--莫尔积分
- 格式:ppt
- 大小:3.16 MB
- 文档页数:37



![[理学]材料力学复习](https://img.taocdn.com/s1/m/490d26fb0c22590102029d43.png)

中南大学2021年全国硕士研究生入学考试948《材料力学》考试大纲本考试大纲由土木工程学院教授委员会于2020年7月 9日通过。
I.考试性质材料力学是工科院校工程力学、土木工程、机电工程、交通运输、地质采矿和材料科学等各专业的一门重要技术基础课。
材料力学考试是为高等院校和科研院所招收硕士研究生而设置的具有选拔性质的全国统一入学考试科目,其目的是科学、公平、有效地测试学生掌握大学本科阶段材料力学课程的基本知识、基本理论,分析方法和实验能力,要求考生能熟练掌握材料力学的基础理论,具有分析和处理杆件的强度、刚度和稳定性等问题的能力,保证被录取者具有较好的分析和解决工程问题的基本素质,有利于各高等院校和科研院所在专业上的择优选拔。
II.考查目标要求考生明确材料力学的研究对象、基本假设,掌握材料力学的基本理论、分析和解决问题的基本方法,具有熟练应用材料力学的分析方法、解决简单工程实际问题的综合能力。
具体要求考生:1、对材料力学的基本概念、基础理论和基本分析方法有明确的认识。
2、能熟练地绘出杆件在基本变形下的内力图,并进行应力、强度、变形和刚度计算。
3、掌握应力状态分析和强度理论,掌握组合变形下杆件的强度的计算。
4、掌握简单超静定问题的求解方法。
5、熟悉能量法的基本原理,掌握计算位移的能量方法。
6、了解压杆的稳定性概念,掌握轴向受压杆的临界力与临界应力的计算方法。
7、掌握构件作等加速运动、匀速转动及受冲击作用时的应力和变形计算方法。
Ⅲ.考试形式和试卷结构1、试卷满分及考试时间本试卷满分为150 分,考试时间为180 分钟2、答题方式答题方式为闭卷,笔试。
3、试卷内容轴向拉伸与压缩、剪切与扭转约15 %截面几何性质约 5 %弯曲内力、弯曲应力、弯曲变约30 %组合变形、应力和应变状态分析、强度理论约20 %能量方法、静不定结构约10 %动载荷约10 %压杆稳定约10 %Ⅳ.试卷题型结构证明题和计算题。
Ⅴ.考查内容(一)材料力学概述材料力学的任务与该课程同相关学科的关系,变形固体的基本假设,截面法和内力,应力、变形、应变的概念。
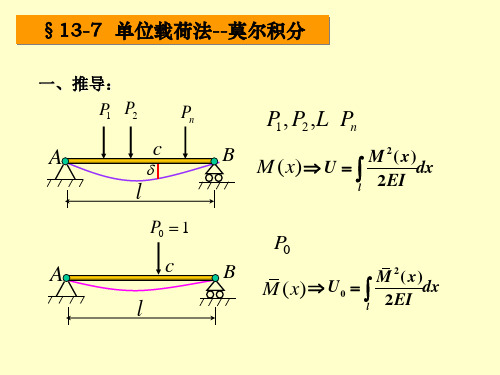
根据虚功原理计算结构位移的一种方法,因用到虚设的单位载荷而得名,又称虚功法。
单位载荷法的最大方便之处在于,如果要求构件任意位置、任意方向上的位移,只要将单位虚力取成与位移相一致的方向并加到该点上就可以了。
如果要求两点之间的相对变形,只有在这两点上加相对单位载荷,然后采用单位载荷法求解。
单位载荷法是英国的J.C.麦克斯韦于1864年、德国的O.莫尔干1874年分别独立提出,故又称麦克斯韦-莫尔法。
它常用于解决杆、杆系结构和薄壁结构的问题,对静定结构和静不定结构都适用。
单位载荷法的原理如下:设结构上作用一个真实的广义力系(见广义力)Pi(i=1,2…,n),并产生变形(图1),欲求结构上j点在Pi作用下的位移,可在j点处加一虚设的单位载荷Pj=1。
该虚设载荷的形式必须同所求位移相对应。
求线位移时,虚设载荷取单位力;求角位移时,虚设载荷取单位力矩。
根据虚功原理,Pj=1在实际力系Pi引起的沿Pj方向的位移△ji上所作的外虚功△ji,在数值上等于Pj引起的内力在实际变形过程中所作的内虚功(包括弯曲的内虚功、拉伸或压缩的内虚功和剪切内虚功) ,即上式右端有两组广义内力:M、N、Q分别为实际载荷引起的弯矩、轴力和剪力;,,分别为虚设单位载荷引起的弯矩,轴力和剪力;K是与结构截面形状有关的系数;ds为结构跨度微元;为求和号,表示对所有构件求和;E、G分别为材料的杨氏模量和剪切模量;A为构件的截面积;I为构件截面的惯性矩。
关于内力的正负号有如下规定:轴力N以拉为正;剪力Q以使结构微段顺时针转动为正;弯矩M只规定乘积的正负号,当M和使杆件同侧纤维受拉时,取正号。
根据各类结构的特点,位移计算公式可作相应简化:①桁架位移计算公式:式中l为桁架中所考虑杆件的长度。
服从胡克定律,有dxV EI x) (轴向拉压扭转22C P =311)P 2ni ii δ==∑对于线弹性体,比例加载的情况是正确的。
弹性体力学的普遍定理之一。
对于线弹性体,第一力系在第二力系所引起的相应位移上所做的功,等于第二力系在第一力系引起的相应位移上的所作的功。
)n 3)互等定理也是弹性体力学的普遍kkCF V ∆=∂∂克劳迪—恩格赛定理将弹性体的余应变能V C 表示为广义力{F}的函数时,余应变能V C 对任一广义力F k 的偏导数等于该力作用点处、沿力方向的位移Δk 。
kkF V ∆=∂∂ε卡氏第二定理将线弹性体的应变能V Ɛ表示为广义力{F}的函数时,应变能V Ɛ对任一广义力F k 的偏导数等于该力作用点处、沿力方向的位移Δk 。
例14-4 图示刚架ABC ,AB 、BC 各段的弯曲刚度均为EI ,试求自由端A 处承受铅垂集中力P 作用时,A 端截面的转角θ。
BAP aaC例14-12 悬壁梁受分布力q 作用,求B 点挠度。
ABql例14-11 刚架两杆抗弯刚度为EI ,试求C 点水平位移ΔHC 。
BAPba C参考书1.S.T. Timoshenko, James.M. Gere (Stanford University), “Mechanics ofMaterials”,Van Nostrand Reinhold Company Ltd., London.1972, 1984, 1990, 1997, 20012.孙训方《材料力学》(四版),高等教育出版社,2002年。
3.[美]R.C.Hibbeler, 汪越胜译,《材料力学》2003,电子工业出版社,20064.苏翼林《材料力学》(二版,上、下册),高等教育出版社,1987年。
三版,天津大学出版社,2001年5月。
5.刘鸿文《材料力学》(四版),高等教育出版社,2003年。
6.清华大学《材料力学习题集》北京:人民教育出版社,1978年。
莫尔积分法计算公式推导莫尔积分法的公式推导。
莫尔积分法是一种常见的数值积分方法,它通过将被积函数展开为一组基函数的线性组合,然后利用基函数的正交性质来进行积分计算。
在本文中,我们将详细推导莫尔积分法的公式,以便更好地理解这一数值积分方法的原理和应用。
1. 基函数展开。
首先,我们假设被积函数f(x)可以展开为一组基函数φi(x)的线性组合,即。
f(x) = Σi=1n ciφi(x)。
其中ci为展开系数,φi(x)为基函数。
我们要求基函数φi(x)在积分区间[a, b]上是正交的,即。
∫a^b φi(x)φj(x) dx = 0, i ≠ j。
这样,我们就可以利用基函数的正交性质来简化积分计算。
2. 莫尔积分公式。
根据莫尔积分法的原理,我们可以将被积函数f(x)在积分区间[a, b]上进行展开,得到。
f(x) = Σi=1n ciφi(x)。
然后,我们将被积函数f(x)乘以基函数φj(x),并在积分区间[a, b]上进行积分,得到。
∫a^b f(x)φj(x) dx = Σi=1n ci∫a^b φi(x)φj(x) dx。
由于基函数φi(x)在积分区间[a, b]上是正交的,即∫a^b φi(x)φj(x) dx = 0, i ≠j,因此上式右边的求和只有在i = j时才会有非零项,即。
∫a^b f(x)φj(x) dx = cj∫a^b φj(x)φj(x) dx。
这样,我们就得到了莫尔积分法的公式:cj = ∫a^b f(x)φj(x) dx / ∫a^b φj(x)φj(x) dx。
3. 数值计算。
莫尔积分法的公式可以用于数值计算被积函数f(x)在积分区间[a, b]上的积分值。
具体地,我们可以选择一组合适的基函数φi(x),计算出展开系数ci,然后利用展开系数ci和基函数φi(x)的正交性质来进行积分计算。
常见的基函数包括Legendre多项式、Chebyshev多项式、Hermite多项式等,它们在不同的积分区间和被积函数下有不同的适用性。