空间中的平行直线

空间直线的位置关系直线是几何学中基本的图形之一，它是由无数个点连结而成的。

而空间直线则是三维空间中的一条直线，具有独特的位置关系。

本文将探讨空间直线的位置关系，通过几个具体案例来加深理解。

一、平行关系如果两条直线在三维空间中永不相交，那么它们被称为平行直线。

平行直线具有以下特点：1. 方向相同：平行直线不会发生交叉或相交，它们的方向是相同的；2. 距离相等：平行直线之间的距离始终保持不变；3. 永不相交：无论空间多大，这两条直线都不会相交。

例如，在三维坐标系中，直线AB与直线CD平行。

这意味着AB与CD的方向相同，两者之间的距离保持不变，且两条直线永远不会相交。

二、垂直关系如果一条直线与平面的交角为90度，那么该直线与平面垂直。

垂直直线与平面之间的位置关系具有以下特点：1. 方向垂直：垂直直线与平面相互垂直，不存在交叉的部分；2. 交角为90度：垂直直线与平面的交角始终为90度；3. 交点唯一：垂直直线与平面只会有一个交点。

举个例子，设有一条通过点A的直线与平面P垂直，那么这条直线满足上述特点：与平面P相交的线段AO为垂直直线，直线AO与平面P的交角为90度，且直线AO与平面P的交点O是唯一的。

三、相交关系两条直线的交点是它们在三维空间中相互交汇的位置。

两条直线的位置关系可以分为以下几种情况：1. 有且仅有一个交点：两条不平行的直线在三维空间中相交，且只有一个交点；2. 无交点：两条不平行的直线在三维空间中没有交点；3. 重合：两条直线在三维空间中完全重合，有无数个交点。

例如，直线l1与直线l2相交于点O，这意味着直线l1和l2在三维空间中有且仅有一个交点。

又如，直线m与直线n平行，它们在三维空间中没有交点。

结论空间直线的位置关系可以通过平行关系、垂直关系和相交关系来描述。

平行关系指的是两条直线永不相交，具有相同的方向和距离；垂直关系指的是直线与平面之间的交角为90度，只有一个交点；相交关系指的是直线之间存在交点，可以是一个或无穷个。

空间几何中的平行关系在空间几何中，平行关系是一种重要而基础的数学概念。

平行关系常常出现在我们的日常生活和工作中，例如平行线、平行四边形等。

本文旨在介绍空间几何中平行关系的定义和性质，并探讨平行关系在实际问题中的应用。

一、平行关系的定义在空间几何中，平行关系是指两条或多条线段或线的方向相同，永不相交的关系。

给定两条直线l1和l2，在平面上，如果l1和l2除了一个公共点之外，其他点都不相交，那么我们就说l1和l2平行。

同样地，在空间中，如果两条直线l1和l2除了一个公共点之外，其他点都不相交，那么我们就说l1和l2平行。

二、平行关系的性质1. 平行关系是传递的。

如果直线l1与直线l2平行，直线l2与直线l3平行，则直线l1与直线l3也平行。

2. 平行关系是对称的。

如果直线l1与直线l2平行，则直线l2与直线l1平行。

3. 平行关系是自反的。

任意一条直线与自身平行。

4. 如果两个平行线分别与一条横截线相交，那么所得的对应角相等。

基于以上性质，我们可以利用平行关系进行推理和证明。

在解决几何问题时，通过判断线段或线的平行关系，我们可以简化问题，找到更加简洁和优雅的解决方法。

三、平行关系在实际问题中的应用在日常生活和工作中，平行关系的应用广泛而深入。

以下是一些平行关系的典型应用示例：1. 建筑工程：在建筑设计和施工中，平行关系的应用非常常见。

例如，在设计一座桥梁时，需要确保桥墩和主梁是平行的，以保证结构的稳定性和美观性。

2. 路网规划：在城市交通规划中，平行道路的设计可以提高交通效率和道路利用率。

平行的道路可以更好地满足不同方向的交通需求，减少交通堵塞和拥堵。

3. 平行投影：在工程和科学领域中，平行投影广泛应用于制图和测量中。

通过选择适当的平行方向，我们可以更准确地表达三维物体的形状和大小。

4. 机械设计：在机械设计中，平行关系的应用可以确保机器部件的精确安装和运动。

例如，在设计一台车床时，需要保证主轴和工作台的平行关系，以确保加工的精度和质量。

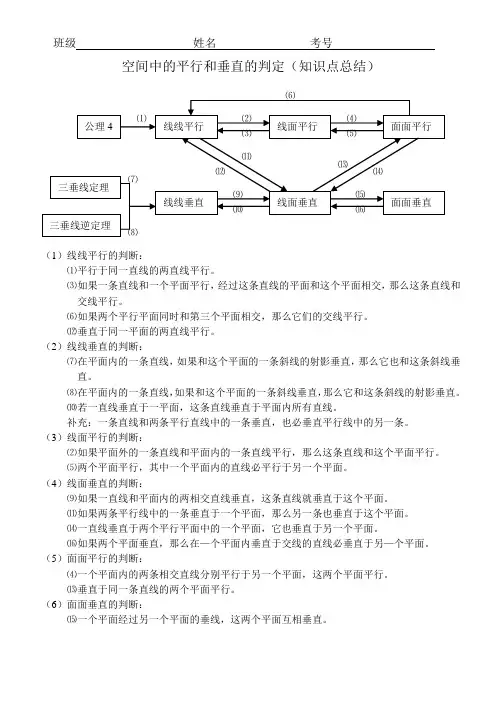
班级姓名考号
空间中的平行和垂直的判定（知识点总结）
（1）线线平行的判断：
⑴平行于同一直线的两直线平行。

⑶如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和
交线平行。

⑹如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

⑿垂直于同一平面的两直线平行。

（2）线线垂直的判断：
⑺在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂
直。

⑻在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它和这条斜线的射影垂直。

⑽若一直线垂直于一平面，这条直线垂直于平面内所有直线。

补充：一条直线和两条平行直线中的一条垂直，也必垂直平行线中的另一条。

（3）线面平行的判断：
⑵如果平面外的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行。

⑸两个平面平行，其中一个平面内的直线必平行于另一个平面。

（4）线面垂直的判断：
⑼如果一直线和平面内的两相交直线垂直，这条直线就垂直于这个平面。

⑾如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面。

⒁一直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。

⒃如果两个平面垂直，那么在—个平面内垂直于交线的直线必垂直于另—个平面。

（5）面面平行的判断：
⑷一个平面内的两条相交直线分别平行于另一个平面，这两个平面平行。

⒀垂直于同一条直线的两个平面平行。

（6）面面垂直的判断：
⒂一个平面经过另一个平面的垂线，这两个平面互相垂直。

空间两平行直线距离公式全文共四篇示例，供读者参考第一篇示例：在几何学中，我们知道两条直线是平行的，当且仅当它们永远不会相交。

平行直线在数学中起着重要的作用，许多几何问题和定理都涉及到平行直线。

而在空间几何中，判断两条直线是否平行，以及计算它们之间的距离，是我们经常需要进行的操作之一。

空间两平行直线距离的计算是一个常见问题，我们可以利用向量和投影的方法来解决。

在空间中，我们可以将两条平行直线表示为：l1: r = a + λv1l2: r = b + μv2其中a和b是两条直线上的固定点，v1和v2分别为两条直线的方向向量。

而λ和μ为参数，用于确定两条直线上的任意点。

为了计算两条平行直线之间的距离，我们首先需要找到直线l2上的一个任意点Q，然后将直线l2上的任意点Q投影到直线l1上得到P 点，这样我们就可以在空间中得到一个由点P和Q确定的向量PQ，即要计算的两条平行直线之间的距离。

然后，我们可以通过向量的计算方法来计算向量PQ的模长，即两条平行直线之间的距离。

利用向量PQ的模长可以得到两条直线之间的距离公式如下：在实际问题中，我们可以直接使用各式数学软件或计算工具来进行计算，避免繁琐的手工计算过程。

但理解两条平行直线之间的距离公式的原理，对于加深对空间几何的理解是非常有帮助的。

总结一下，空间两平行直线距离的计算方法涉及到向量和投影的原理，通过寻找两条直线上的任意点，并计算其投影向量的模长，即可求得两条平行直线之间的距离。

在实际问题中，我们可以借助数学工具来进行快速、准确的计算，提高工作效率。

对于数学爱好者和学生来说，掌握空间两平行直线距离的计算方法，可以帮助他们更好地理解空间几何学的相关知识，提高数学解题的能力。

第二篇示例：空间中两直线间的距离是我们在几何学中经常遇到的问题。

在平面几何中，两条平行直线的距离很容易计算，只需要找到两条直线上任意一点到另一条直线的垂直距离即可。

但是在空间几何中，情况就显得复杂许多。

空间中的平行一、知识梳理<一>线线平行与线面平行1.线线平行：定义：空间中两直线共面且没有交点，则两直线平行.证明两直线平行的主要方法是：①三角形中位线平行并等于底边的一半；②平行四边形两组对边分别平行；③梯形的一组对边平行；④直线平行的传递性：若a//b,b//c,则a//c.2.线面平行定义：若直线和平面没有交点，则称直线和平面平行.判定1：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.（只需在平面内找一条直线和平面外的直线平行就可以）////a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭判定2:两平面平行，一平面上的任一条直线与另一个平面平行.a a a a αβαββααβ⇒⇒⊂⊂⎫⎫⎬⎬⎭⎭或线面平行的性质：如果一条直线平行于一个平面，经过这条直线的平面与这个平面相交，那么这条直线和它们的交线平行.<二>面面平行1.定义：若两个平面没有交点，则两个平面平行2.判断：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行.,,a b a b A a b αααβββ⊂⊂⎫⎪=⇒⎬⎪⎭,,,a b a b A a a b b a b ααββ⊂⎫⎪=⎪⇒⎬''⎪⎪''⊂⎭判定定理的推论： 一个平面内的两条相交直线与另一个平面上的两条直线分别平行，两平面平行.3.两平面平行的性质： 性质Ⅰ：如果一个平面与两平行平面都相交，那么它们的交线平行.a ab b αβαγβγ=⇒=⎫⎪⎬⎪⎭性质Ⅱ：平行于同一平面的两平面平行；性质Ⅲ：夹在两平行平面间的平行线段相等；,,A C AC BD B D AB CD αβαβ∈⇒=∈⎫⎪⎪⎬⎪⎪⎭二、典例精析【例1】如图所示的几何体中，△ABC 是任意三角形，AE ∥CD ，且AE ＝AB ＝2a ，CD ＝a ，F 为BE 的中点．求证：DF ∥平面ABC .【练习】如图，已知P 是平行四边形ABCD 所在平面外一点，M 、N 分别是AB 、PC 的中点．求证：MN ∥平面P AD .【例2】已知正方形ABCD 所在的平面和正方形ABEF 所在的平面相交与AB ，M 、N 分别是AC 、BF 上的中点.求证：MN//平面BCE .【练习】如图，在四棱锥P-ABCD 中，底面ABCD 为矩形，E 为PD 的上一点，且PE=2ED ．若F 为PE 的中点.求证：BF ∥平面AEC .【例3】如图，四棱锥P-ABCD 中，底面ABCD 为梯形，AB ∥DC ，AB ⊥BC ．AB =BC=22AD ，点E 在棱PB 上，且PE=2EB ．求证：PD ∥平面EAC .【练习】如图，正四棱锥P-ABCD 中，PA=AB ，点M ，N 分别在PA ，BD 上，且31==BD BN PA PM .求证：MN ∥平面PBC .2【例4】a ，b ，c 为三条不重合的直线，α，β，γ为三个不重合平面，现给出六个命题①a ∥c ，b ∥c ⇒a ∥b ②a ∥γ ，b ∥γ ⇒a ∥b ③α∥c ，β∥c ⇒α∥β④ α∥γ ，β∥γ ⇒α∥β ⑤α∥c ，a ∥c ⇒α∥a ⑥α∥γ ，a ∥γ ⇒α∥a其中正确的命题是（ ）A.①②③⑥ B ．①④⑤ C ．①④ D ．①④⑥【练习】下面六个命题中正确命题的个数是（ ）①如果a 、b 是两条直线，b a //，那么a 平行于经过b 的任何一个平面；②如果直线a 和平面α满足a //α,那么a 与平面α内的任何一条直线平行；③如果直线a //α,b //α,那么b a //；④如果直线a 、b 和平面α满足b a //，a //α，α⊄b ，那么b //α；⑤如果直线a 与平面α上的无数条直线平行，则a //α；⑥如果平面α的同侧有两点A 、B 到平面α的距离相等，则AB //α.A. 0B. 1C. 2D. 3【例5】一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是（ ）A ．异面B ．相交C ．平行D ．不能确定【练习】直线a //平面α，α内有n 条直线交于一点，这n 条直线直线中与直线a 平行的直线（ ）A.至少有一条 B ．至多有一条 C ．有且只有一条 D ．没有三、课后练习1．已知直线a ∥平面α，P α∈，那么过点P 且平行于α的直线（ ）A ．只有一条，不在平面α内B ．有无数条，不一定在α内C ．只有一条，且在平面α内D ．有无数条，一定在α内 2．若夹在两个平面间的三条平行线段相等，则这两个平面位置关系是（ ）A ．平行B ．相交C ．相交或平行D ．以上答案都不对3．下列结论中正确的是（ ） ①α∥β，β∥γ，则α∥γ；②过平面外一条直线有且只有一个平面与已知平面平行；③平面外的两条平行线中，如果有一条和平面平行，那么另一条也和这个平面平行；④如果一条直线与两个平行平面中一个相交，那么它与另一个必相交.A ．①②③B ．②③④C ．①③④D ．①②③④4．a ，b 是两条异面直线，A 是不在a ，b 上的点，则下列结论成立的是( )A ．过A 且平行于a 和b 的平面可能不存在B ．过A 有且只有一个平面平行于a 和bC ．过A 至少有一个平面平行于a 和bD ．过A 有无数个平面平行于a 和b5．如果平面α外有两点A 、B ，它们到平面α的距离都是a ，则直线AB 和平面α的位置关系是( )A ．平行B ．相交C ．平行或相交D ．AB ⊂α6.如图所示，在棱长为a 的正方体1111ABCD A BC D -中，E ，F ，P ，Q 分别是BC ，11C D ，1AD ，BD 的中点.(1)求证：PQ //平面11DCC D ；(2)在DC 上找一点H ，使EFH //平面11BB D D .7.如图，在空间四边形ABCD 中，P 、Q 分别是ABC ∆和BCD ∆的重心.求证：PQ ∥平面ACD .8.如图所示，已知三棱锥BCD A -被一平面所截，截面为平行四边形EFGH ，求证：（1）//EF 平面BCD ；（2）CD EF //.。

空间直线平行的判定定理空间直线平行的判定定理引言在空间几何中，直线是一种基本的几何对象。

而直线的平行是一个重要的概念，它在许多问题中都有着重要的应用。

因此，研究如何判定空间直线是否平行，是空间几何中重要的一部分。

定义在空间几何中，两条直线如果在同一平面内且不相交，则这两条直线互相平行。

定理有以下三种方法可以判定空间直线是否平行：方法一：向量法向量法是判定两条空间直线是否平行最常用的方法之一。

具体步骤如下：1. 求出两条直线上任意两点构成的向量；2. 判断这两个向量是否共线；3. 如果这两个向量共线，则这两条直线平行；否则不平行。

方法二：斜率法斜率法是判定两条空间直线是否平行另外一种常用的方法。

具体步骤如下：1. 对于每一条直线，求出其在某个坐标系下的方程；2. 求出每一条直线在该坐标系下的斜率；3. 如果两条直线斜率相等，则这两条直线平行；否则不平行。

方法三：距离法距离法是判定两条空间直线是否平行的另外一种方法。

具体步骤如下：1. 求出两条直线上任意一点的坐标；2. 求出这两个点之间的距离；3. 如果这两个点之间的距离为0，则这两条直线平行；否则不平行。

应用空间直线的平行在许多问题中都有着重要的应用。

例如，在建筑设计中，需要对建筑物进行测量和设计，而在测量和设计过程中需要考虑到空间直线的平行关系。

再如，在工程制图中，需要将三维物体投影到二维纸面上，而在投影过程中也需要考虑空间直线的平行关系。

结论通过向量法、斜率法和距离法可以判定空间直线是否平行。

在实际问题中，可以根据具体情况选择不同的方法进行判定。

空间直线的平行关系在许多问题中都有着重要的应用，在实际问题中需要注意其合理性和准确性。

【高考导航】本节所涉及到的知识点：直线平行公理、异面直线的概念以及异面直线所成的角是高考考查的重点.考查的题型比较灵活.如1993，全国理，18题；1994，上海，14题；1995，全国文，10题；1996，全国，19题.试题分值4～5分，多以难度系数较大的题为主.【学法点拨】本节共有两个知识点：平行直线、异面直线.平行直线主要是将平行公理和平行线的传递性推广到空间，并引出平移的概念，学习时要意识到并非所有在平面图形中适用的结论，对于立体图形仍应适用.例如没有公共点的直线在平面上是平行关系，在空间中考虑就有平行与异面两种位置关系.对于异面直线要理解不同在任何一个平面内，它们构成一个空间图形，绝不是平面图形，异面直线的夹角是由两条相交直线的夹角的概念扩充而成.计算异面直线a 、b 的夹角大小，必须通过平移转化为相交直线a ′，b′的夹角，实现转化的手段是“平移”.【基础知识必备】 一、必记知识精选1.空间两条不重合的直线的三种位置关系. (1)相交直线——共面有且仅有一个公共点. (2)平行直线——共面没有公共点. (3)异面直线——不同在任一平面内.2.平行公理：平行于同一条直线的两直线平行.c b c a b a ∥∥∥⇒⎭⎬⎫. 3.等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等.4.异面直线判定定理：连结平面内一点与平面外一点的直线，和这个平面内不经过此点的直线是异面直线.5.异面直线的概念及异面直线所成角：已知两条异面直线a 、b ，经过空间任一点O 作直线a′∥a,b′∥b,a′与b ′所成的锐角或直角叫做异面直线所成角.异面直线所成角的范围为(0,2π]. 二、重点难点突破1.掌握平行公理并能熟练应用；了解公理4是证明直线平行的主要依据.2.异面直线的概念，异面直线所成角的概念及求法.注意概念中异面直线所成角与“O ”点位置无关，因此，在实践中“O ”点常取在两条异面直线中的一条上.（二）难点1.异面直线的判定.利用异面直线判定定理，或排除平行、相交两种位置关系进行判断，或利用反证法.2.异面直线所成角.求异面直线所成角，是按定义先作出它们所成的角，然后一般通过解三角形来求角.三、易错点和易忽略点导析 1.对定理的掌握不准确. 【例1】 如果角A 的两边与角B 的两边分别平行，则角A 与角B 的关系是 .错解：A=B.正确解法：A=B 或A+B=π.错解分析：在利用等角定理时忽略了“方向相同”这一条件.对概念的把握不深刻. 2.空间概念不牢固.【例2】 在空间中，垂直于同一条直线的两条直线的位置关系是（ ） A.平行 B.垂直C.异面D.以上答案都不对 错解:A 正确解法:D错解分析：以固有的平面思维对待空间问题，本题中两条直线的位置关系是平行、相交或异面.【综合应用创新思维点拨】 一、学科内综合思维点拨【例1】 已知两直线a,b 是异面直线，a 上有两点A 、C 中，b 有两点B 、D.求证AB 和CD 是异面直线.思维入门指导：证明两直线a 、b 异面，其实质是证明使a ⊂α，b ⊂α的平面α是不存在的.一般有两种方法：反证法和利用异面直线判定定理进行证明.证明：假设AB 与CD 不是异面直线，则AB 、CD 共面. 设AB ⊂α，CD ⊂α，则A ∈α，C ∈α. 又∵A ∈α，C ∈α， ∴AC ⊂α.即a ⊂α.同理b ⊂α，这与a 、b 异面矛盾.故假设不成立，则直线AB 和CD 是异面直线.点拨：反证法是证明否定命题的基本方法.反证法证明过程一般有如下几个步骤：(1)反设：作出与命题结论相反的假设；(2)归谬：将反设和条件进行推理,得出矛盾；(3)结论：肯定原命题正确.在立体几何中，下面三类问题常用反证法.(1)直接利用公理、定义证题，即在尚未建立有关定理作为依据的情况下证题. (2)证明某些惟一性结论的命题. (3)所证结论是一种否定性的命题. 二、应用思维点拨【例2】 已知：长方体ABCD —A ′B ′C ′D ′中AB=a ，BC=b ，AA ′=c(a ＞b)，求异面直线D ′B 和AC 所成角的余弦值.思维入门指导：欲求两条异面直线所成的角，关键在于选择恰当的点，通过平移一条直线后，转化为平面问题，利用解三角形求之.解法一：如图9-2-1，连接BD 交AC 于E ，取DD ′的中点F,连结EF ，则EF ∥21D ′B.∴∠FEA 是D ′B 和AC 所成的角.连接AF ，∵AE=422b a +=222b a +,EF=21D ′B=2222c b a ++,AF=2422c b +,∴在△FEA 中，cos∠FEA=AE EF AF AE EF ∙-+2222=))((2222222c b a b a b a +++-.∵a ＞b ，∴cos ∠FEA＞0. ∴D ′B 与AC 所成角的余弦值为))((2222222c b a b a b a +++-.解法二：在长方体的一旁，补上一个全等的长方体，如图9-2-2，则BE ∥AC,∠D′BE为D ′B 和AC 所成角或其补角.∵D ′B=222c b a ++,BE=22b a +,D′E=224c a +, ∴在△D ′BE 中，cos ∠D ′BE=BE B D E D BE B D ∙''-+'2222=))((2222222c b a b a b a ++++-.∵a ＞b,则b 2-a 2＜0,即cos ∠D ′BE ＜0. 故D ′B 与AC 所成角的余弦值为))((2222222c b a b a b a +++-.点拨:求异面直线所成角的基本法则是“作平行线，构造三角形”.而在采用平移找角,转化为三角形求解时,应时刻注意两条异面直线所成的角的范围为(0,2π],因为常常会出现所找的角为异面直线所成角的补角.三、创新思维点拨【例3】 如图9-2-3,A 是△BCD 所在平面外一点，M 、N 分别是△ABC 和△ACD 的重心，若BC=5，CD=8，∠BCD=60°，求MN 的长.思维入门指导：由题设中的条件M 、N 分别为三角形重心，可预想解题过程要利用三角形的中线及重心的性质进行解题.解：连结AM 并延长交BC 于点E ，连结AN 并延长交CD 于点F ，则E 、F 分别为BC 、CD的中点，连结EF ，则EF ∥21BD. ∵32==AF AN AE AM ,∴MN ∥EF.∴MN ∥31BD. 在△BCD 中，BC=5，CD=8，∠BCD=60°， ∴BD 2=BC 2+CD 2-2BC ·CD ·cos60°=25+64-2×5×8×21 =49. 则BD=7.∴MN=37. 点拨：本题是一道好题，其创新之处是将重心的性质及平行公理有机地结合在一起. 四、高考思维点拨【例4】 （2003，北京春招，5分）如图9-2-4，在正三角形ABC 中，D 、E 、F 分别为各边的中点，G 、H 、I 、J 分别为AF 、AD 、BE 、DE 的中点，将△ABC 沿DE 、EF 、DF 折成三棱锥以后,GH 与IJ 所成角的度数为（ ）A.90°B.60°C.45°D.0°思维入门指导：本题是折叠类问题，解答此类问题的基本思路是：先作出折叠前与折叠后的图形.注意折叠前后元素之间的位置关系，数量关系的变化，然后解答.解：如图9-2-5所示，折叠后A 、B 、C 重合，记为点K ，GH 与IJ 为异面直线.K(A 、B 、C)∵GH ∥DF ，IJ ∥KD ，∴∠KDF 为GH 与IJ 所成角. ∵∠KDF=60°，∴GH 与IJ 所成角的度数为60°，选B.点拨：把平面物体折叠成空间几何体的过程中，始终在同一个平面内的点与线，线与线的位置关系及数量关系不变,若折叠前后不在同一个平面内,则位置关系及数量关系都可能发生变化.五、经典类型题思维点拨【例5】 设A 、B 、C 、D 是不共面的四个点，P 、Q 、R 、S 分别是AC 、BC 、DB 、DA 的中点，如图9-2-6，若AB=122，CD=43,且四边形PQRS 的面积为123，求异面直线AB 和CD 所成的角.思维入门指导：利用中位线的性质，将异面直线所成的角转化为相交的两条直线所成的角，然后求解.解：∵P 、Q 是AC 、BC 的中点，∴PQ ∥21AB. ∵Q 、R 是BC 、BD 的中点, ∴QR ∥21CD.同理RS ∥21AB,PS ∥21CD. ∴四边形PQRS 为平行四边形，且∠PQR 是异面直线AB 与CD 所成的角或其补角. ∴PQ=62，QR=23.S □PQRS ＝PQ ·QR ·sin ∠PQR ＝62·23·sin ∠PQR ＝123, ∴sin ∠PQR=22. 故异面直线AB 、CD 所成角为45°.点拨：异面直线是立体几何的重点和难点之一，几乎每年都被考查.考查的内容涉及定义、所成角两方面，其中异面直线所成角为考查的热点.六、探究性学习点拨【例6】 如图9-2-7，空间四边形ABCD 的两条对角线AC 、BD 所成角为θ，AC=a ，BD=b （a,b 为常数），E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点，当θ为何值时，四边形EFGH 的面积S 最大？最大值为多少？思维入门指导:四边形EFGH 面积的大小是由边的长度及内角的度数决定的,先将四边形EFGH 的面积表示为θ的函数,再利用函数求最值.解:∵E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点,∴EF ∥HG ∥AC,且EF=HG=21AC; EH ∥FG ∥BD,且EH=FG=21BD. ∴四边形EFGH 是一个平行四边形,且EF=21a,FG=21b. ∵AC 与BD 所成角为θ，∴∠EFG=θ.∴S=EF ·FG ·sin θ=41absin θ. ∵θ∈(0,2π),∴当θ=2π时,S max =41ab. 点拨：顺次连结不共面的四点A 、B 、C 、D 所组成的四边形叫做空间四边形，空间四边形各边中点连结形成的平行四边形中有以下结论：（1）当AC=BD 时，为菱形；（2）当AC ⊥BD 时，为矩形;（3）当AC ⊥BD ，AC=BD 时，为正方形.【同步达纲训练】A 卷:教材跟踪练习题 （60分45分钟） 一、选择题（每小题5分，共30分）1.如果a 、b 是异面直线，c ∥a ，那么c 与b （ ） A.一定是异面直线 B.一定是相交直线 C.不可能是平行直线 D.不可能是相交直线2.两条直线不相交是两条直线异面的（ ）A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分又不必要条件 3.空间四边形的对角线互相垂直且相等，顺次连接这个空间四边形各边中点所形成的四边形是（ ）A.梯形B.矩形C.正方形D.菱形4.正方体的一条对角线与正方体的棱可以组成异面直线的对数是（ ） A.2 B.3 C.6 D.125.一个角的两边与另一角的两边分别垂直,则这两个角（ ）A.相等B.互补C.相等或互补D.不能确定6.正方体AC 1中，E 、F 分别是AB 、BB 1的中点，则A 1E 与C 1F 所成角的余弦值为（ ）A.21 B.22 C.52D.521二、填空题(每小题4分,共16分)7.点A 是△BCD 所在平面外一点，M 、N 、P 分别是△ABC 、△ACD 、△ABD 的重心,且S △BCD =9,则△MNP 的面积为 .8.正方体六个面内的所有对角线中,互成60°角的对角线共有 对. 9.若a ∥b,c ⊥a,d ⊥b.则c 与d 的位置关系是 .10.过异面直线a 与b 外的点P.与a 、b 都垂直的直线的条数是 . 三、解答题(每小题7分,共14分)11.已知空间四边形ABCD 的对角线AC=10，BD=6，M 、N 分别是AB 、CD 的中点，MN=7，求异面直线AC 与BD 所成角.12.如图9-2-8在四面体A —BCD 中，AB=AC=AD=26a ，BC=CD=a,BD=2a ，点F 是BD 的中点，求AF 与CD 所成的角的大小.B 卷:综合应用创新练习题 （70分60分钟） 一、学科内综合题（5分）1.两条异面直线所成角为θ，则有（ ） A.0＜cos θ≤1 B.0≤cos θ＜1 C.0≤sin θ＜1 D.0≤sin θ≤1 二、应用题（5分）2.空间四边形ABCD 中，M 、N 分别是AB 、CD 的中点，设21(BC+AD)=l ,则（ ） A.MN ＞l B.MN ＜lC.MN=lD.MN 与l 的大小关系不确定 三、创新题（55分）（一）教材变型题（5分） 3.（P 15第5题变型）和两条异面线AB 、CD 都相交的两条直线a 、b 的位置关系是（ ） A.平行 B.异面 C.相交 D.以上都不对 （二）一题多解（1O 分）4.证明：对边平方和相等的空间四边形的对角线互相垂直. （三）一题多变（20分）5.两条异面直线a 、b 所成的角是60°，过空间任意一点O 与a 、b 都成60°角的直线的条数是( )A.2条B.3条C.4条D.不能确定(1)一变:两条异面直线a 、b 所成的角是60°,过空间任意一点O 与a 、b 都成50°角的直线有 条.(2)二变:两条异面直线a 、b 所成的角是θ，过空间任意一点O 与a 、b 都成45°角的直线有两条.则θ的取值范围是 .(3)三变:两条异面直线a 、b 所成的角是60°，过空间一点O 的直线l 与a 、b 所成的角都是θ,则θ的取值范围是 .(四)新解法题(10分)6.已知棱长为a 的正方体AC 1中，E 、F 分别为BC 、A 1D 1的中点，求AF 与DE 所成的角. (五)新情境题(10分)7.A 、B 、C 、D 是异面直线AB 、CD 上的点，线段AB=CD=4，M 为AC 的中点,N 为BD 的中点，MN=3，求异面直线AB 、CD 所成角的余弦值.四、高考题8.（1995，全国，5分）如图9-2-9，ABCD —A 1B 1C 1D 1是正方体，B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是（ ）A.1715 B.21 C.178D.23加试题：竞赛趣味题（10分）（1999，全国联赛）给定下列两个关于异面直线的命题: 命题Ⅰ：若平面α上的直线a 与平面β上的直线b 为异面直线，直线c 是α、β的交线，那么c 至多与a 、b 中的一条相交.命题Ⅱ：不存在这样的无穷多条直线，它们中的任意两条都是异面直线.那么（ ） A.命题Ⅰ正确，命题Ⅱ不正确 B.命题Ⅱ正确，命题Ⅰ不正确 C.两个命题都正确 D.两个命题都不正确【课外阅读】多面体的截面用一个平面去截几何体，此平面与几何体的交集，叫做这个几何体的截面.此平面与几何体表面的交集(交线)叫做截线.此平面与几何体的棱的交集（交点）叫做截点.作多面体截面的关键在于确定截点，有了位于多面体同一表面上的两个截点即可连结成截线，从而求得截面.作截线与截点的主要根据有： (1)确定平面的条件.(2)如果两个不重合的平面有一个公共点，那么它们相交于过此点的一条直线.(3)如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内. (4)如果一条直线平行于一个平面，经过这条直线的平面与这个平面相交，那么这条直线就和交线平行.(5)如果两个平面平行，第三个平面和它们相交，那么两条交线平行. 主要画法是交线法，即求出截面所在的平面与多面体某一表面所在平面的交线，再找出各有关截线（或其延长线）与此交线的交点.【例1】 如图9-2-10，正方体ABCD —A 1B 1C 1D 1中，E 、F 、G 分别在AB 、BC 、DD 1上，求作过E 、F 、G 三点的截面.作法:(1)在底面AC 内，过E 、F 作直线EF 分别与DA 、DC 的延长线交于点L 、M. (2)在侧面A 1D 内，连结LG 交AA 1于点K. (3)在侧面D 1C 内，连结GM 交CC 1于点H. (4)连结KE 、FH.则五边形EFHGK 即为所求的截面.有时为了便于作截面，还须引进辅助面作为作图的中介.【例2】如图9-2-11，正方体ABCD—A1B1C1D1中，E、F在两条棱上,G在底面A1C1内，求作过E、F、G的截面.作法:(1)在底面A1C1内,过G作PQ∥B1C1，交棱于P、Q两点.(2)作辅助面PBCQ，在此面内，过G、F作直线交BP的延长线于M.(3)在侧面A1B内,连结ME，交A1B1于K.(4)在底面A1C1内,连结KG，延长交B1C1于H.(5)连结HF.(6)在底面AC内，作FL∥HK，交AB于L.(7)连结EL.则五边形ELFHK为所求的截面.此外，对于面数较多的多面体，可以把其中一些表面伸展构成面数较少的多面体，使作图得解.【例3】如图9-2-12，五棱锥P—ABCDE中，三条侧棱上各有一已知点F、G、H，求作过F、G、H的截面.作法:(1)将侧面PAB、PBC、PDE伸展得到三棱锥P—BST.(2)在侧面PBS内，连结并延长GF，交PS于K.(3)在侧面PBT内，连结并延长GH交PT于L.(4)在侧面PST内，连结KL分别交PD、PE于M、N.(5)连结FN、MH.则五边形FGHMN即为所求的截面.参考答案A卷一、1.C 点拨：若c∥b，又c∥a，则a∥b，与a、b异面矛盾.2.A 点拨：两条直线异面一定不相交，但不相交也可以是平行.3.C 点拨:如答图9-2-1所示，E 、F 、G 、H 分别为空间四边形ABCD 各边的中点.则EF ∥21AC ，HG ∥21AC.则EF∥HG.∴四边形EFGH 为平行四边形. ∵AC=BD ，∴EF=HE.∵AC ⊥BD ，∴EF ⊥HE.∴四边形EFGH 为正方形.4.C 点拨：除相交的6条棱外，其余6条棱均与之成异面直线.5.D 点拨：两者共在一个平面内则相等或互补，若一个角在另一个角平面外，且一条边垂直于第一个角所在平面，则两角关系不能确定.6.C 点拨:如答图9-2-2所示，取B 1G=41A 1B 1，连结GF ，GC 1,则∠C 1FG 即为A 1E 与C 1F 所成的角.设AA 1=a ，则在△C 1GF 中，C 1F=25a,GF=45a,C 1G=417a. ∴cos ∠C 1FG=852161716545⨯-+=52.二、7.1 点拨：如答图9-2-3，连结AM 并延长交BC 于点E ，则E 为BC 中点.同理可得CD 边中点F,BD 边中点G,则32===AG AP AF AN AE AM . ∴MN ∥EF ，MP ∥EG ，NP ∥GF ，且MP=32EG. 又∵EF ∥21BD,∴S △MNP =94·S △EGF =94·41S △BCD =94×41×9=1. 8.24 点拨:一个顶点对应3对,故共有3×8=24对.9.平行、相交或异面 点拨:可以在正方体中找出此题的实物模型,另外此题等价于判断垂直于同一条直线的两条直线间的位置关系.10.1条 点拨:两条异面直线有一条公垂线,过直线外一点与直线平行的直线有且只有一条，所以过点P 可以作一条直线与公垂线平行.三、11.解：如答图9-2-4，取BC 的中点E ，连结ME 、NE.则ME ∥21AC,NE ∥21BD. ∴∠MEN 就是异面直线AC 与BD 所成角或其补角. 在△MEN 中,ME=21AC=5,NE=21BD=3,MN=7, ∴cos∠MEN=NEME MN NE ME ∙-+2222=-21.∴AC 与BD 所成角为60°.12.解：如答图9-2-5，取BC 的中点E ，连EF 、AE ，∵F 为BD 的中点,∴EF ∥21CD. ∴∠AFE 为异面直线AF 、CD 所成的角或补角，且EF=21a ，在△ABC 中,AB=AC=26a,BC=a. ∴AE 2=AB 2-(21BC)2=46a 2-41a 2=45a 2. 在△ABD 中,AB=AD=26a,BD=2a, ∴AF 2=AB 2-(21BD)2=46a 2-42a 2=a 2. 在△AFE 中，cos ∠AFE=EFAF AE EF AF ∙-+2222=0,∴∠AFE=90°.∴异面直线AF 与CD 成90°的角.B 卷一、1.B 点拨：两条异面直线所成角的范围为（O ，2π]. 二、2.B 点拨：取AC 的中点为E ，连结ME,NE ，则在△MNE 中，21(BC+AD)=ME+NE ＞MN ，即MN ＜l .三、(一)3.D 点拨：可能存在异面与相交两种情况.(二)4.已知：如答图9-2-6中，AB 2+CD 2=BC 2+AD 2. 求证:AC ⊥BD.证法一：回归定义，所成角为90°，作角计算.如答图9-2-6(1)，分别取AB 、CD 、DA 的中点E 、F 、G ，则有EG ∥BD ，FG ∥AC ，这样问题就演变为证明△EFG 为直角三角形.因为题设为数量关系，故可考虑通过计算△EFG 的各边长来解决，记AB 、BC 、CD 、DA 、AC 、BD的长分别为a 、b 、c 、d 、m 、n,则EG=21n,FG=21m.在△ACD 和△BCD 中分别求出中线AF 和BF 的长，再进一步在△AFB 中求出中线EF 的长，比较EF 、FG 、GE 的关系即可解决问题.证法二：遵循化归思想，该问题也可考虑构造平行四边形ENFG （如答图9-2-6(2)）,通过证NG=EF 来证明其为矩形.遵循条件集中的原则取各棱中点并顺次连结构造四边形NPGQ 和四边形EPFQ ，使已知量——四边形四条边与求解对象——NG 和EF 建立联系.可证四边形NPGQ 和四边形EPFQ 均为平行四边形.在平行四边形EPFQ 和NPGQ 中，EF 2+PQ 2=EP 2+PF 2+FQ 2+QE 2=2[(21b)2+(21d)2], NG 2+PQ 2=NQ 2+QG 2+GP 2+PN 2=2[(21a)2+(21c)2]. ∵a 2+c 2=d 2+b 2,∴EF 2+PG 2=NG 2+PQ 2.∴EF=NG.∴平行四边形ENFG 为矩形.证法三:(学习第四节后再看)遵循化归思想，该问题也可以转化为线面垂直来证明,作AH ⊥BD ，连结CH(如答图9-2-6(3)),只要证明CH ⊥BD 即可.在△ABD 中,cos ∠ABD=an d n a 2222-+,∴BH=a ·cos ∠ABD=n d n a 2222-+.在△BCD 中,cos ∠CBH=bnc n b 2222-+.∵a 2+c 2=d 2+b 2,∴cos∠CBH=nbd n a 2222-+=BC BH.∴∠BHC=90°.(三)5.B 点拨：过O 分别作a 、b 的平行线a ′、b′,则a′b′的夹角为60°.与a 、b 成等角只需与a ′、b ′成等角即可.如答图9-2-7所示，与a 、b 都成60°的直线一条是l ，另外两条是过点O 在a ′、b′所确定平面外，理论依据是最小角定理.(1)2 (2)θ∈(0,2π) (3)θ∈[6π,2π](四)6.解:如答图9-2-8，连结C 1E ，DC 1,则∠C 1ED 为AF 与DE 所成角或其补角.在△C 1DE 中，DE=C 1E=25a ，DC 1=2a ， cos∠C 1ED=222245224545αααα⨯-+=51,∴AF 与DE 所成角为arccos 51.(五)7.解:如答图9-2-9，连结BC ，取BC 的中点E ，连结ME,NE.则在△ABC 中，ME ∥21AB ，ME=2. 在△BCD 中，NE ∥21CD,NE=2. 故∠MEN 为AB 、CD 所成角或它的补角. ∵cos ∠MEN=NE ME MN NE ME ∙∙-+2222=81-,∴AB 、CD 所成角为arccos 81.四、8.A 点拨:如答图9-2-10,将DF 1平移至AG 1,A 1G 1=411B A .再将AG 1平移至EE 1,其中AE=2AB,B 1E 1=411B A .则∠BE 1E 即是异面直线BE 1与DF 1所成的角.Cos∠BE 1E=11221212EE BE BE EE BE ∙-+=1715.加试题:D 点拨:命题Ⅰ中c 与a 、b 可以都相交，只要交点不重合亦为异面直线;命题Ⅱ中的异面直线可以有无穷多条.且两两互为异面直线.。

三维空间两直线平行公式在三维空间中，两条直线平行的条件是它们的方向向量相同。

以下将详细解释两直线平行的公式及其证明。

设直线L1过点P1(x1,y1,z1)且方向向量为V1(a1,b1,c1)；直线L2过点P2(x2,y2,z2)且方向向量为V2(a2,b2,c2)。

我们需要证明的是，若V1与V2平行，即V1与V2的方向向量成比例，那么直线L1与直线L2平行。

根据向量的平行性质，若两个向量成比例，它们的任意一个分量除以对应分量都应该等于同一个常数。

因此，我们可以写出以下方程组：a1/a2=b1/b2=c1/c2我们将分别解这三个方程：1.a1/a2=b1/b2：将这两个比例化简，得到a1b2=a2b1、可以通过跨乘积来验证这个方程。

向量V1和V2的跨乘积定义为：V1×V2=(b1c2-b2c1,a2c1-a1c2,a1b2-a2b1)根据跨乘积的定义，我们可以看到(a1b2-a2b1)=0，即a1b2=a2b1、因此，第一个比例式成立。

2.b1/b2=c1/c2：类似地，将这两个比例化简，得到b1c2=b2c1、同样使用跨乘积来验证这个方程。

根据跨乘积的定义，我们可以得到(b1c2-b2c1)=0，即b1c2=b2c1、因此，第二个比例式成立。

3.a1/a2=c1/c2：类似地，将这两个比例化简，得到a1c2=a2c1、同样使用跨乘积来验证这个方程。

根据跨乘积的定义，我们可以得到(a2c1-a1c2)=0，即a1c2=a2c1、因此，第三个比例式成立。

通过以上的验证，我们可以得出结论：若V1与V2平行，即V1与V2的方向向量成比例，那么直线L1与直线L2平行。

综上所述，两条直线平行的条件为它们的方向向量成比例。

这个条件可以用比例方程组a1/a2=b1/b2=c1/c2来表示。

我们可以利用这个条件来判断两条直线是否平行，并且可以通过分析方向向量之间的比例关系来计算直线的平行性。

1.平行直线平行公理：过直线外一点有且只有一条直线和已知直线平行.基本性质4：平行于同一条直线的两条直线互相平行.等角定理：如果一个角的两边与另一个角的两边分别对应平行，并且方向相同，那么这两个角相等.2.直线与平面平行判定性质定义定理图形条件a∩α＝∅a⊂α，b⊄α，a∥b a∥αa∥α，a⊂β，α∩β＝b结论a∥αb∥αa∩α＝∅a∥b3.平面与平面平行判定性质定义定理图形条件α∩β＝∅a⊂β，b⊂β，a∩b＝P，a∥α，b∥αα∥β，α∩γ＝a，β∩γ＝b α∥β，a⊂β结论α∥βα∥βa∥b a∥α【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的一条直线，则这条直线平行于这个平面.(×)(2)若一条直线平行于一个平面，则这条直线平行于这个平面内的任一条直线.(×)(3)如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行.(×)(4)如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面.(√)(5)若直线a与平面α内无数条直线平行，则a∥α.(×)(6)若α∥β，直线a∥α，则a∥β.(×)1.一条直线l上有相异三个点A、B、C到平面α的距离相等，那么直线l与平面α的位置关系是()A.l∥αB.l⊥αC.l与α相交但不垂直D.l∥α或l⊂α答案 D解析当距离不为零时，l∥α，当距离为零时，l⊂α.2.设α，β，γ为三个不同的平面，m，n是两条不同的直线，在命题“α∩β＝m，n⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题.①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ.可以填入的条件有()A.①或②B.②或③C.①或③D.①或②或③答案 C解析由面面平行的性质定理可知，①正确；当n∥β，m⊂γ时，n和m在同一平面内，且没有公共点，所以平行，③正确.故选C.3.(教材改编)下列命题中正确的是()A.若a，b是两条直线，且a∥b，那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α，那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a，b和平面α满足a∥b，a∥α，b⊄α，则b∥α答案 D解析A中，a可以在过b的平面内；B中，a与α内的直线可能异面；C中，两平面可相交；D中，由直线与平面平行的判定定理知，b∥α，正确.4.(教材改编)如图，正方体ABCD－A1B1C1D1中，E为DD1的中点，则BD1与平面AEC的位置关系为________.答案平行解析连接BD，设BD∩AC＝O，连接EO，在△BDD1中，O为BD的中点，所以EO为△BDD1的中位线，则BD 1∥EO ，而BD 1⊄平面ACE ，EO ⊂平面ACE ， 所以BD 1∥平面ACE .5.过三棱柱ABC －A 1B 1C 1任意两条棱的中点作直线，其中与平面ABB 1A 1平行的直线共有________条. 答案 6解析 各中点连线如图，只有面EFGH 与面ABB 1A 1平行，在四边形EFGH 中有6条符合题意.题型一 直线与平面平行的判定与性质 命题点1 直线与平面平行的判定例1 如图，四棱锥P －ABCD 中，AD ∥BC ，AB ＝BC ＝12AD ，E ，F ，H 分别为线段AD ，PC ，CD 的中点，AC 与BE 交于O 点，G 是线段OF 上一点. (1)求证：AP ∥平面BEF ； (2)求证：GH ∥平面P AD . 证明 (1)连接EC ， ∵AD ∥BC ，BC ＝12AD ，∴BC 綊AE ，∴四边形ABCE 是平行四边形， ∴O 为AC 的中点.又∵F 是PC 的中点，∴FO ∥AP ， FO ⊂平面BEF ，AP ⊄平面BEF ， ∴AP ∥平面BEF . (2)连接FH ，OH ，∵F ，H 分别是PC ，CD 的中点， ∴FH ∥PD ，∴FH ∥平面P AD .又∵O 是BE 的中点，H 是CD 的中点， ∴OH ∥AD ，∴OH ∥平面P AD .又FH ∩OH ＝H ，∴平面OHF ∥平面P AD .又∵GH ⊂平面OHF ，∴GH ∥平面P AD . 命题点2 直线与平面平行性质定理的应用例2 (2014·安徽)如图，四棱锥P －ABCD 的底面是边长为8的正方形，四条侧棱长均为217.点G ，E ，F ，H 分别是棱PB ，AB ，CD ，PC 上共面的四点，平面GEFH ⊥平面ABCD ，BC ∥平面GEFH . (1)证明：GH ∥EF ；(2)若EB ＝2，求四边形GEFH 的面积.(1)证明 因为BC ∥平面GEFH ，BC ⊂平面PBC ， 且平面PBC ∩平面GEFH ＝GH ， 所以GH ∥BC .同理可证EF ∥BC ，因此GH ∥EF .(2)解 如图，连接AC ，BD 交于点O ，BD 交EF 于点K ，连接OP ，GK . 因为P A ＝PC ，O 是AC 的中点，所以PO ⊥AC ， 同理可得PO ⊥BD .又BD ∩AC ＝O ，且AC ，BD 都在底面内， 所以PO ⊥底面ABCD .又因为平面GEFH ⊥平面ABCD ， 且PO ⊄平面GEFH ，所以PO ∥平面GEFH . 因为平面PBD ∩平面GEFH ＝GK ，所以PO ∥GK ，且GK ⊥底面ABCD ，从而GK ⊥EF . 所以GK 是梯形GEFH 的高.由AB ＝8，EB ＝2得EB ∶AB ＝KB ∶DB ＝1∶4， 从而KB ＝14DB ＝12OB ，即K 为OB 的中点.再由PO ∥GK 得GK ＝12PO ，即G 是PB 的中点，且GH ＝12BC ＝4.由已知可得OB ＝42，PO ＝PB 2－OB 2＝68－32＝6， 所以GK ＝3.故四边形GEFH 的面积 S ＝GH ＋EF 2·GK ＝4＋82×3＝18.如图所示，在四棱锥P －ABCD 中，∠ABC ＝∠ACD ＝90°，∠BAC＝∠CAD ＝60°，E 为PD 的中点，AB ＝1，求证：CE ∥平面P AB .证明由已知条件有AC＝2AB＝2，AD＝2AC＝4，CD＝2 3.如图所示，延长DC，AB，设其交于点N，连接PN，因为∠NAC＝∠DAC＝60°，AC⊥CD，所以C为ND的中点，又因为E为PD的中点，所以EC∥PN，因为EC⊄平面P AB，PN⊂平面P AB，所以CE∥平面P AB.思维升华判断或证明线面平行的常用方法：(1)利用线面平行的定义(无公共点)；(2)利用线面平行的判定定理(a⊄α，b⊂α，a∥b⇒a∥α)；(3)利用面面平行的性质定理(α∥β，a⊂α⇒a∥β)；(4)利用面面平行的性质(α∥β，a⊄β，a∥α⇒a∥β).题型二平面与平面平行的判定与性质例3如图所示，在三棱柱ABC－A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：(1)B，C，H，G四点共面；(2)平面EF A1∥平面BCHG.证明(1)∵G，H分别是A1B1，A1C1的中点，∴GH是△A1B1C1的中位线，∴GH∥B1C1.又∵B1C1∥BC，∴GH∥BC，∴B，C，H，G四点共面.(2)∵E，F分别是AB，AC的中点，∴EF∥BC.∵EF⊄平面BCHG，BC⊂平面BCHG，∴EF∥平面BCHG.∵A1G綊EB，∴四边形A1EBG是平行四边形，∴A1E∥GB.∵A1E⊄平面BCHG，GB⊂平面BCHG，∴A1E∥平面BCHG.∵A1E∩EF＝E，∴平面EF A1∥平面BCHG.引申探究1.在本例条件下，若D为BC1的中点，求证：HD∥平面A1B1BA.证明如图所示，连接HD，A1B，∵D为BC1的中点，H为A1C1的中点，∴HD∥A1B，又HD⊄平面A1B1BA，A1B⊂平面A1B1BA，∴HD∥平面A1B1BA.2.在本例条件下，若D1，D分别为B1C1，BC的中点，求证：平面A1BD1∥平面AC1D.证明如图所示，连接A1C交AC1于点M，∵四边形A1ACC1是平行四边形，∴M是A1C的中点，连接MD，∵D为BC的中点，∴A1B∥DM.∵A1B⊂平面A1BD1，DM⊄平面A1BD1，∴DM∥平面A1BD1.又由三棱柱的性质知，D1C1綊BD，∴四边形BDC1D1为平行四边形，∴DC1∥BD1.又DC1⊄平面A1BD1，BD1⊂平面A1BD1，∴DC1∥平面A1BD1，又∵DC1∩DM＝D，DC1，DM⊂平面AC1D，∴平面A1BD1∥平面AC1D.思维升华证明面面平行的方法：(1)面面平行的定义；(2)面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行；(3)利用垂直于同一条直线的两个平面平行；(4)两个平面同时平行于第三个平面，那么这两个平面平行；(5)利用“线线平行”“线面平行”“面面平行”的相互转化.如图，在正方体ABCD—A1B1C1D1中，S是B1D1的中点，E、F、G分别是BC、DC、SC的中点，求证：(1)直线EG∥平面BDD1B1；(2)平面EFG∥平面BDD1B1.证明(1)如图，连接SB，∵E，G分别是BC，SC的中点，∴EG∥SB.又∵SB⊂平面BDD1B1，EG⊄平面BDD1B1，∴直线EG∥平面BDD1B1.(2)连接SD，∵F，G分别是DC，SC的中点，∴FG∥SD.又∵SD⊂平面BDD1B1，FG⊄平面BDD1B1，∴FG∥平面BDD1B1，又EG⊂平面EFG，FG⊂平面EFG，EG∩FG＝G，∴平面EFG∥平面BDD1B1.题型三平行关系的综合应用例4在正方体ABCD—A1B1C1D1中，如图.(1)求证：平面AB1D1∥平面C1BD；(2)试找出体对角线A1C与平面AB1D1和平面C1BD的交点E，F，并证明A1E＝EF＝FC.(1)证明因为在正方体ABCD—A1B1C1D1中，AD綊B1C1，所以四边形AB1C1D是平行四边形，所以AB1∥C1D.又因为C1D⊂平面C1BD，AB1⊄平面C1BD，所以AB1∥平面C1BD.同理，B1D1∥平面C1BD.又因为AB1∩B1D1＝B1，AB1⊂平面AB1D1，B1D1⊂平面AB1D1，所以平面AB1D1∥平面C1BD.(2)解如图，连接A1C1交B1D1于点O1，连接AO1，与A1C交于点E.因为AO1⊂平面AB1D1，所以点E也在平面AB1D1内，所以点E就是A1C与平面AB1D1的交点.连接AC交BD于点O，连接C1O，与A1C交于点F，则点F就是A1C与平面C1BD的交点.下面证明A1E＝EF＝FC.因为平面A1C1C∩平面AB1D1＝EO1，平面A1C1C∩平面C1BD＝C1F，平面AB1D1∥平面C1BD，所以EO 1∥C 1F ，在△A 1C 1F 中，O 1是A 1C 1的中点， 所以E 是A 1F 的中点，即A 1E ＝EF .同理可证OF ∥AE ，所以F 是CE 的中点，即FC ＝EF ， 所以A 1E ＝EF ＝FC .思维升华 (1)线面平行和面面平行的性质都体现了转化思想.(2)对较复杂的综合结论问题往往需要反复运用线面平行的判定定理和性质定理来进行证明，有如下方法： 线线平行―――――→在平面内找或作一直线线面平行 ―――――――――→经过直线找或作平面与已知平面的交线线线平行 如图所示，四棱锥P －ABCD 的底面是边长为a 的正方形，侧棱P A ⊥底面ABCD ，在侧面PBC 内，有BE ⊥PC 于E ，且BE ＝63a ，试在AB 上找一点F ，使EF ∥平面P AD .解 如图所示，在平面PCD 内，过E 作EG ∥CD 交PD 于G ， 连接AG ，在AB 上取点F ，使AF ＝EG ， ∵EG ∥CD ∥AF ，EG ＝AF ， ∴四边形FEGA 为平行四边形， ∴FE ∥AG .又AG ⊂平面P AD ，FE ⊄平面P AD ， ∴EF ∥平面P AD . ∴F 即为所求的点.又P A ⊥面ABCD ，∴P A ⊥BC ， 又BC ⊥AB ，∴BC ⊥面P AB . ∴PB ⊥BC .∴PC 2＝BC 2＋PB 2＝BC 2＋AB 2＋P A 2. 设P A ＝x 则PC ＝2a 2＋x 2， 由PB ·BC ＝BE ·PC 得： a 2＋x 2·a ＝2a 2＋x 2·63a ，∴x ＝a ，即P A ＝a ，∴PC ＝3a . 又CE ＝a 2－(63a )2＝33a ，∴PE PC ＝23，∴GE CD ＝PE PC ＝23， 即GE ＝23CD ＝23a ，∴AF ＝23a .即AF ＝23AB .故点F 是AB 上靠近B 点的一个三等分点.5.立体几何中的探索性问题典例 (12分)如图，在四棱锥S －ABCD 中，已知底面ABCD 为直角梯形，其中AD ∥BC ，∠BAD ＝90°，SA ⊥底面ABCD ，SA ＝AB ＝BC ＝2.tan ∠SDA ＝23.(1)求四棱锥S －ABCD 的体积；(2)在棱SD 上找一点E ，使CE ∥平面SAB ，并证明. 规范解答解 (1)∵SA ⊥底面ABCD ，tan ∠SDA ＝23，SA ＝2，∴AD ＝3.[2分]由题意知四棱锥S －ABCD 的底面为直角梯形，且SA ＝AB ＝BC ＝2，[4分] V S －ABCD ＝13×SA ×12×(BC ＋AD )×AB＝13×2×12×(2＋3)×2＝103.[6分] (2)当点E 位于棱SD 上靠近D 的三等分点处时，可使CE ∥平面SAB .[8分] 证明如下：取SD 上靠近D 的三等分点为E ，取SA 上靠近A 的三等分点为F ，连接CE ，EF ，BF ， 则EF 綊23AD ，BC 綊23AD ，∴BC 綊EF ，∴CE ∥BF .[10分] 又∵BF ⊂平面SAB ，CE ⊄平面SAB ， ∴CE ∥平面SAB .[12分]解决立体几何中的探索性问题的步骤 第一步：写出探求的最后结论. 第二步：证明探求结论的正确性. 第三步：给出明确答案.第四步：反思回顾，查看关键点、易错点和答题规范.温馨提醒(1)立体几何中的探索性问题主要是对平行、垂直关系的探究，对条件和结论不完备的开放性问题的探究，解决这类问题一般根据探索性问题的设问，假设其存在并探索出结论，然后在这个假设下进行推理论证，若得到合乎情理的结论就肯定假设，若得到矛盾的结论就否定假设.(2)这类问题也可以按类似于分析法的格式书写步骤：从结论出发“要使……成立”，“只需使……成立”.[方法与技巧]1.平行问题的转化关系2.直线与平面平行的主要判定方法(1)定义法；(2)判定定理；(3)面与面平行的性质.3.平面与平面平行的主要判定方法(1)定义法；(2)判定定理；(3)推论；(4)a⊥α，a⊥β⇒α∥β.[失误与防范]1.在推证线面平行时，一定要强调直线不在平面内，否则会出现错误.2.在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而在应用性质定理时，其顺序恰好相反，但也要注意，转化的方向总是由题目的具体条件而定，决不可过于“模式化”.3.解题中注意符号语言的规范应用.A组专项基础训练(时间：35分钟)1.平面α∥平面β，点A，C∈α，B，D∈β，则直线AC∥直线BD的充要条件是()A.AB∥CDB.AD∥CBC.AB与CD相交D.A，B，C，D四点共面答案 D解析充分性：A，B，C，D四点共面，由平面与平面平行的性质知AC∥BD.必要性显然成立.2.(2015·安徽)已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是()A.若α，β垂直于同一平面，则α与β平行B.若m，n平行于同一平面，则m与n平行C.若α，β不平行，则在α内不存在与β平行的直线D.若m，n不平行，则m与n不可能垂直于同一平面解析 对于A ，α，β垂直于同一平面，α，β关系不确定，故A 错；对于B ，m ，n 平行于同一平面，m ，n 关系不确定，可平行、相交、异面，故B 错；对于C ，α，β不平行，但α内能找出平行于β的直线，如α中平行于α，β交线的直线平行于β，故C 错；对于D ，若假设m ，n 垂直于同一平面，则m ∥n ，其逆否命题即为D 选项，故D 正确.3.设l 为直线，α，β是两个不同的平面.下列命题中正确的是( )A.若l ∥α，l ∥β，则α∥βB.若l ⊥α，l ⊥β，则α∥βC.若l ⊥α，l ∥β，则α∥βD.若α⊥β，l ∥α，则l ⊥β答案 B解析 l ∥α，l ∥β，则α与β可能平行，也可能相交，故A 项错；由“同垂直于一条直线的两个平面平行”可知B 项正确；由l ⊥α，l ∥β可知α⊥β，故C 项错；由α⊥β，l ∥α可知l 与β可能平行，也可能l ⊂β，也可能相交，故D 项错.故选B.4.给出下列关于互不相同的直线l 、m 、n 和平面α、β、γ的三个命题：①若l 与m 为异面直线，l ⊂α，m ⊂β，则α∥β；②若α∥β，l ⊂α，m ⊂β，则l ∥m ；③若α∩β＝l ，β∩γ＝m ，γ∩α＝n ，l ∥γ，则m ∥n .其中真命题的个数为( )A.3B.2C.1D.0答案 C解析 ①中当α与β不平行时，也可能存在符合题意的l 、m ；②中l 与m 也可能异面；③中⎩⎪⎨⎪⎧ l ∥γl ⊂αα∩γ＝n⇒l ∥n ，同理，l ∥m ，则m ∥n ，正确.5.下列四个正方体图形中，A ，B 为正方体的两个顶点，M ，N ，P 分别为其所在棱的中点，能得出AB ∥平面MNP 的图形的序号是( )A.①③B.①④C.②③D.②④解析①中易知NP∥AA′，MN∥A′B，∴平面MNP∥平面AA′B可得出AB∥平面MNP(如图).④中，NP∥AB，能得出AB∥平面MNP.6.在四面体A－BCD中，M，N分别是△ACD，△BCD的重心，则四面体的四个面中与MN平行的是________. 答案平面ABD与平面ABC解析如图，取CD的中点E，连接AE，BE.则EM∶MA＝1∶2，EN∶BN＝1∶2，所以MN∥AB.所以MN∥平面ABD，MN∥平面ABC.7.将一个真命题中的“平面”换成“直线”、“直线”换成“平面”后仍是真命题，则该命题称为“可换命题”.给出下列四个命题：①垂直于同一平面的两直线平行；②垂直于同一平面的两平面平行；③平行于同一直线的两直线平行；④平行于同一平面的两直线平行.其中是“可换命题”的是________.(填命题的序号)答案①③解析由线面垂直的性质定理可知①是真命题，且垂直于同一直线的两平面平行也是真命题，故①是“可换命题”；因为垂直于同一平面的两平面可能平行或相交，所以②是假命题，不是“可换命题”；由基本性质4可知③是真命题，且平行于同一平面的两平面平行也是真命题，故③是“可换命题”；因为平行于同一平面的两条直线可能平行、相交或异面，故④是假命题，故④不是“可换命题”.8.如图，在正四棱柱ABCD－A1B1C1D1中，E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点，N是BC的中点，动点M在四边形EFGH上及其内部运动，则M满足条件________时，有MN∥平面B1BDD1.答案M∈线段FH解析因为HN∥BD，HF∥DD1，所以平面NHF∥平面B1BDD1，故线段FH上任意点M与N相连，都有MN∥平面B1BDD1.(答案不唯一)9.如图，ABCD与ADEF为平行四边形，M，N，G分别是AB，AD，EF的中点. 求证：(1)BE∥平面DMF；(2)平面BDE∥平面MNG.证明(1)如图，连接AE，则AE必过DF与GN的交点O，连接MO，则MO为△ABE的中位线，所以BE∥MO，又BE⊄平面DMF，MO⊂平面DMF，所以BE∥平面DMF.(2)因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥GN，又DE⊄平面MNG，GN⊂平面MNG，所以DE∥平面MNG.又M为AB中点，所以MN为△ABD的中位线，所以BD∥MN，又BD⊄平面MNG，MN⊂平面MNG，所以BD∥平面MNG，又DE与BD为平面BDE内的两条相交直线，所以平面BDE∥平面MNG.10.如图，E、F、G、H分别是正方体ABCD－A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证：(1)EG∥平面BB1D1D；(2)平面BDF∥平面B1D1H.证明(1)取B1D1的中点O，连接GO，OB，易证四边形BEGO为平行四边形，故OB∥GE，由线面平行的判定定理即可证EG∥平面BB1D1D.(2)由题意可知BD∥B1D1.如图，连接HB、D1F，易证四边形HBFD1是平行四边形，故HD1∥BF.又B1D1∩HD1＝D1，BD∩BF＝B，所以平面BDF∥平面B1D1H.B组专项能力提升(时间：20分钟)11.设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是()A.若α⊥β，m⊂α，n⊂β，则m⊥nB.若α∥β，m⊂α，n⊂β，则m∥nC.若m⊥n，m⊂α，n⊂β，则α⊥βD.若m⊥α，m∥n，n∥β，则α⊥β答案 D解析A中，m与n可垂直、可异面、可平行；B中m与n可平行、可异面；C中若α∥β，仍然满足m⊥n，m⊂α，n⊂β，故C错误；故D正确.12.空间四边形ABCD的两条对棱AC、BD的长分别为5和4，则平行于两条对棱的截面四边形EFGH在平移过程中，周长的取值范围是________.答案(8,10)解析 设DH DA ＝GH AC ＝k ，∴AH DA ＝EH BD＝1－k ， ∴GH ＝5k ，EH ＝4(1－k )，∴周长＝8＋2k .又∵0<k <1，∴周长的范围为(8,10).13.在三棱锥S －ABC 中，△ABC 是边长为6的正三角形，SA ＝SB ＝SC ＝15，平面DEFH 分别与AB ，BC ，SC ，SA 交于D ，E ，F ，H .D ，E 分别是AB ，BC 的中点，如果直线SB ∥平面DEFH ，那么四边形DEFH 的面积为________.答案 452解析 取AC 的中点G ，连接SG ，BG .易知SG ⊥AC ，BG ⊥AC ，SG ∩BG ＝G ，故AC ⊥平面SGB ，所以AC ⊥SB .因为SB ∥平面DEFH ，SB ⊂平面SAB ，平面SAB ∩平面DEFH ＝HD ，则SB ∥HD .同理SB ∥FE .又D ，E 分别为AB ，BC 的中点，则H ，F 也为AS ，SC 的中点，从而得HF 綊12AC 綊DE ，所以四边形DEFH 为平行四边形.又AC ⊥SB ，SB ∥HD ，DE ∥AC ，所以DE ⊥HD ，所以四边形DEFH 为矩形，其面积S ＝HF ·HD ＝(12AC )·(12SB )＝452.14.(2015·四川改编)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.(1)请将字母F ，G ，H 标记在正方体相应的顶点处(不需说明理由)；(2)判断平面BEG 与平面ACH 的位置关系.并证明你的结论.解 (1)点F ，G ，H 的位置如图所示.(2)平面BEG ∥平面ACH ，证明如下：因为ABCD-EFGH 为正方体，所以BC ∥FG ，BC ＝FG ，又FG ∥EH ，FG ＝EH ，所以BC ∥EH ，BC ＝EH ，于是BCHE 为平行四边形，所以BE ∥CH ，又CH ⊂平面ACH ，BE ⊄平面ACH ，所以BE ∥平面ACH ，同理BG ∥平面ACH ，又BE ∩BG ＝B ，所以平面BEG ∥平面ACH .15.如图，已知正方形ABCD 的边长为6，点E ，F 分别在边AB ，AD 上，AE ＝AF＝4，现将△AEF 沿线段EF 折起到△A ′EF 位置，使得A ′C ＝2 6. (1)求五棱锥A ′－BCDFE 的体积； (2)在线段A ′C 上是否存在一点M ，使得BM ∥平面A ′EF ？若存在，求A ′M 的长；若不存在，请说明理由.解 (1)如图所示，连接AC ，设AC ∩EF ＝H ，连接A ′H .因为四边形ABCD 是正方形，AE ＝AF ＝4，所以H 是EF 的中点，且EF ⊥AH ，EF ⊥CH ，从而有A ′H ⊥EF ，CH ⊥EF ，又A ′H ∩CH ＝H ，所以EF ⊥平面A ′HC ，且EF ⊂平面ABCD ，从而平面A ′HC ⊥平面ABCD ，过点A ′作A ′O 垂直HC 且与HC 相交于点O ，则A ′O ⊥平面ABCD ，因为正方形ABCD 的边长为6，AE ＝AF ＝4，故A ′H ＝22，CH ＝42，所以cos ∠A ′HC ＝A ′H 2＋CH 2－A ′C 22A ′H ·CH ＝8＋32－242×22×42＝12， 所以HO ＝A ′H ·cos ∠A ′HC ＝2，则A ′O ＝6，所以五棱锥A ′－BCDFE 的体积V ＝13×(62－12×4×4)×6＝2863.(2)线段A′C上存在点M，使得BM∥平面A′EF，此时A′M＝6 2.证明如下：连接OM，BD，BM，DM，且易知BD过O点.A′M＝62＝14A′C，HO＝14HC，所以OM∥A′H，又OM⊄平面A′EF，A′H⊂平面A′EF，所以OM∥平面A′EF，又BD∥EF，BD⊄平面A′EF，EF⊂平面A′EF，所以BD∥平面A′EF，又BD∩OM＝O，所以平面MBD∥平面A′EF，因为BM⊂平面MBD，所以BM∥平面A′EF.。

空间几何中的平行与垂直关系在空间几何中，平行和垂直是我们常见的几何关系。

平行指两条直线或者两个平面永远不会相交，而垂直指两条直线或者两个平面相互成直角。

这两种关系在数学和实际生活中都有广泛的应用。

本文将探讨平行和垂直的定义、性质以及在几何中的重要应用。

一、平行关系平行线是指两条直线不相交，且永远保持相同的距离。

根据平行线的定义，我们可以得出以下性质：1. 平行线具有传递性，即若线段AB与线段BC平行，则线段AB与线段AC也平行。

2. 平行线之间不存在交点，也不能相互交叉。

3. 平行线与一条直线的交点与另一条直线平行。

4. 平行线具有对称性，即若线段AB与线段CD平行，则线段CD与线段AB也平行。

平行关系在空间几何中有很多应用，比如在平行四边形和三角形的性质证明中经常用到。

平行线也是解决几何难题的重要手段，如求解截面积和体积等问题。

二、垂直关系垂直是指两条直线或者两个平面相互成直角。

根据垂直关系的定义，我们可以得出以下性质：1. 垂直于同一条直线的两条直线彼此平行。

2. 两个平面相互垂直的条件是它们的法向量垂直。

3. 直线与平面垂直，则直线上的任意一条线段与平面上的任意一条线段相互垂直。

垂直关系在几何中也有广泛的应用。

在建筑设计中，垂直关系是测量和布局的基础。

在空间坐标系中，垂直关系可以用来识别空间中的平面，具有重要的实际应用价值。

总结：平行和垂直是空间几何中常见的几何关系。

两条平行线永远不会相交，而两条垂直线相互成直角。

它们在各自的定义中包含了一系列的性质和特点，这些性质和特点为我们解决几何问题提供了重要的线索。

在几何证明中，平行和垂直关系是解决问题的关键步骤之一。

我们可以利用这些关系性质，推导出更多有关几何形状和结构的定理。

在实际生活中，平行和垂直关系也有广泛的应用。

比如在建筑设计、物体测量等方面都需要考虑平行和垂直的关系，以保证结构的稳定性和功能的实现。

通过理解和应用平行和垂直关系，我们可以更好地理解和解决与空间几何相关的问题，提高数学思维能力和几何分析能力。

空间直线1. 空间两条直线的三种位置关系—相交、平行、异面.2. 公理4 平行于同一直线的两条直线互相平行.定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等.推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角（或直角）相等.3．异面直线所成的角直线a，b是异面直线，经过空间任意一点O，分别引直线a′∥a，b′∥b，我们把直线a′和b′所成的锐角（或直角）叫做异面直线a和b所成的角．4．异面直线的距离和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线．两条异面直线的公垂线在这两条异面直线间的线段的长度，叫做两条异面直线的距离．[要点内容]1．空间两条直线的三种位置关系—相交、平行、异面。

相交直线和平行直线都是共面直线，异面直线是立体图形。

2．空间两直线的位置关系分类从有无公共点的角度看，可分为两类：（1）两条直线有且仅有一个公共点—相交直线；3．异面直线概念的理解“不同在任何一个平面内的两条直线”，是指这两条直线不能同时在任何一个平面内。

注意：分别在某两个平面内的两条直线，不一定是异面直线，它们可能是相交直线，也可能是平行直线，如图。

4．异面直线的画法及判定画异面直线时，以平面为衬托，可使两直线不能共面的特点显示得更清楚，如图判定两条直线是异面直线的方法：方法一，利用：“过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线。

”方法二，利用反证法，假设这两条直线不是异面直线，推导出矛盾。

这可能是与公理矛盾、与定理矛盾、与定义矛盾、与已知条件或事实矛盾等。

5．对于两条异面直线所成的角的定义应注意以下几点：（1）取直线a′、b′所成的锐角（或直角）作为异面直线a、b所成的角。

（2）在这个定义中，空间一点是任意选取的，根据等角定理，可以判定异面直线a和b 所成的角和a′和b′所成的锐角（或直角）相等，而与点O的位置无关。

（3）由于异面直线a、b所成的角与点O的位置无关，一般情况下，可将点O取在直线a或b上。