有限元分析1
- 格式:ppt
- 大小:595.50 KB
- 文档页数:2





有限元分析报告(1)有限元仿真分析实验⼀、实验⽬的通过刚性球与薄板的碰撞仿真实验,学习有限元⽅法的基本思想与建模仿真的实现过程,并以此实践相关有限元软件的使⽤⽅法。
本实验使⽤HyperMesh 软件进⾏建模、⽹格划分和建⽴约束及载荷条件,然后使⽤LS-DYNA软件进⾏求解计算和结果后处理,计算出钢球与⾦属板相撞时的运动和受⼒情况,并对结果进⾏可视化。
⼆、实验软件HyperMesh、LS-DYNA三、实验基本原理本实验模拟刚性球撞击薄板的运动和受⼒情况。
仿真分析主要可分为数据前处理、求解计算和结果后处理三个过程。
前处理阶段任务包括:建⽴分析结构的⼏何模型,划分⽹格、建⽴计算模型,确定并施加边界条件。
四、实验步骤1、按照点-线-⾯的顺序创建球和板的⼏何模型(1)建⽴球的模型:在坐标(0,0,0)建⽴临时节点,以临时节点为圆⼼,画半径为5mm的球体。
(2)建⽴板的模型:在tool-translate⾯板下node选择临时节点,选择Y-axis,magnitude输⼊,然后点击translate+,return;再在2D-planes-square ⾯板上选择Y-axis,B选择上⼀步移下来的那个节点,surface only ,size=30。
2、画⽹格(1)画球的⽹格:以球模型为当前part,在2D-atuomesh⾯板下,surfs 选择前⾯建好的球⾯,element size设为,mesh type选择quads,选择elems to current comp,first order,interactive。
(2)画板的⽹格:做法和设置同上。
3、对球和板赋材料和截⾯属性(1)给球赋材料属性:在materials⾯板内选择20号刚体,设置Rho为,E为200000,NU为。
(2)给球赋截⾯属性:属性选择SectShll,thickness设置为,QR设为0。
(3)给板赋材料属性:材料选择MATL1,其他参数:Rho为,E为100000,Nu 为,选择Do Not Export。



第一章 引言§1-1概述1、有限元方法(The Finite Element Method, FEM )是计算机问世以后迅速发展起来的一种分析方法。
众所周知,每一种自然现象的背后都有相应的物理规律,对物理规律的描述可以借助相关的定理或定律表现为各种形式的方程(代数、微分、或积分)。
这些方程通常称为控制方程(Governing equation )。
针对实际的工程问题推导这些方程并不十分困难,然而,要获得问题的解析的数学解却很困难。
人们多采用数值方法给出近似的满足工程精度要求的解答。
有限元方法就是一种应用十分广泛的数值分析方法。
有限元方法是处理连续介质问题的一种普遍方法,离散化是有限元方法的基础。
然而,这种思想自古有之。
齐诺(Zeno 公元前5世纪前后古希腊埃利亚学派哲学家)曾说过:空间是有限的和无限可分的。
故,事物要存在必有大小。
亚里士多德(Aristotle 古希腊大哲学家,科学家)也讲过:连续体由可分的元素组成。
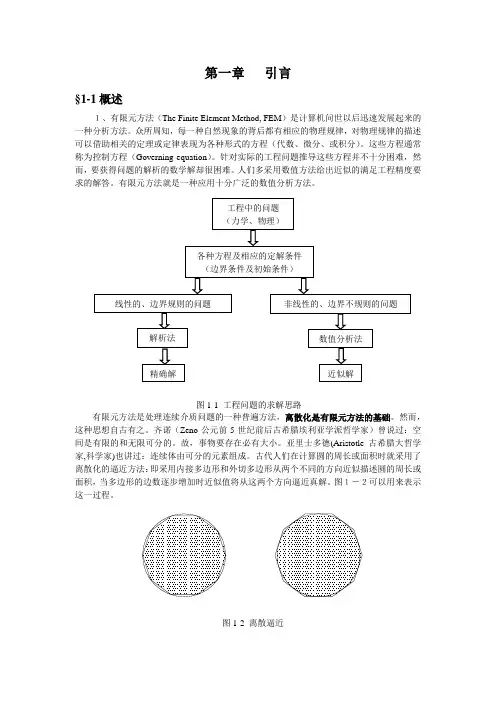
古代人们在计算圆的周长或面积时就采用了离散化的逼近方法:即采用内接多边形和外切多边形从两个不同的方向近似描述圆的周长或面积,当多边形的边数逐步增加时近似值将从这两个方向逼近真解。
图1-2可以用来表示这一过程。
工程中的问题 (力学、物理)各种方程及相应的定解条件(边界条件及初始条件)线性的、边界规则的问题 数值分析法 精确解 近似解 非线性的、边界不规则的问题 解析法 图1-1 工程问题的求解思路图1-2 离散逼近有限单元法 有限差分法图1-3 有限元法与有限差分法比较近代,这一方法首先在航空结构分析中取得了明显的效果:一种称为框架分析法(framework method )被用来分析平面弹性体(将平面弹性体描述为杆和梁的组合体)(1941,Hrenikoff );在采用三角形单元及最小势能原理研究St.Venant 扭转问题时,分片连续函数被用来在子域中近似描述未知函数(1943, Courant )。

有限元分析2篇有限元分析(一)有限元分析(FEA)是将连续物体分割成有限个小单元,通过数值计算得出每个小单元对应的位移和应力,最终得到整体物体的位移、应力和变形状态的一种数值计算方法。
无需将实际工作负载应用于实际结构,便可进行应力测试。
有限元分析具有计算效率高、可重复性好、成本低廉等优点。
有限元分析的第一步是准备几何模型。
几何模型可以使用CAD软件或3D扫描仪等工具创建。
接下来,需要定义材料属性,如密度、弹性模量、泊松比等。
在规定边界条件后,可以将几何模型分割成小单元,如三角形或四边形,每个单元都与简单的微积分计算相关。
使用有限元分析技术,可以计算每个小单元的应力和位移以估算整个结构的应力和位移。
使用有限元分析技术时,需要一个有限元分析软件。
在几何模型、材料属性和边界条件输入完毕后,软件会自动生成数学模型,然后通过斯蒂芬-泊松方程求解每个小单元的应力和位移。
最终,软件将输出结构的应力、位移、变形等结果,这些结果有助于评估结构的稳定性和安全性。
有限元分析广泛应用于工程领域,如建筑、桥梁、飞机、汽车等领域。
它可以帮助工程师评估设计和材料选择,降低成本,提高安全性,节省时间等方面为工程师做出决策提供支持。
有限元分析(二)有限元分析技术(FEA)在现代工程设计中越来越重要,它可以预测物体在受到力的情况下的变形和应力分布。
这种技术可以用于设计复杂机械设备、建筑结构等领域,并有助于开发出更强、更轻、更高效的材料。
有限元分析技术的优点之一是可以对设计进行多次迭代,并可以对结果进行快速可视化分析。
这种技术可以在设计初期发现设计、制造或装配上的问题,以减少失误和实际测试的成本。
随着计算机计算能力的提高,有限元分析技术已经变得越来越快速、准确和精细。
使用有限元分析技术,物理问题可以转化为一个经过离散化的静力学或动力学问题。
它能够处理复杂的初始和边界条件,同时考虑物体的非线性特性和有限的应许值。
这些都是实验室测试不可比拟的优点。
第一节 有限元分析概述对于一般的工程受力问题,希望通过平衡微分方程、变形协调方程、几何方程和本构方程联立求解而获得整个问题的精确解是十分困难的,一般几乎是不可能的。
随着20世纪五六十年代计算机技术的出现和发展、以及工程实践中对数值分析要求的日益增长,并发展起来了有限元的分析方法。
有限元法自1960年由Clough首次提出后,获得了迅速的发展;虽然首先只是应用于结构的应力分析,但很快就广泛应用于求解热传导、电磁场、流体力学、成形工艺等连续问题。
一、有限元法的基本概念对于连续体的受力问题,既然作为一个整体获得精确求解十分困难;于是,作为近似求解,可以假想地将整个求解区域离散化,分解成为一定形状有限数量的小区域(即单元),彼此之间只在一定数量的指定点(即节点)处相互连接,组成一个单元的集合体以替代原来的连续体,如图7-1弯曲凹模的受力分析所示;只要先求得各节点的位移,即能根据相应的数值方法近似求得区域内的其他各场量的分布;这就是有限元法的基本思想。
从物理的角度理解,即将一个连续的凹模截面分割成图7-1所示的有限数量的小三角形单元,而单元之间只在节点处以铰链相连接,由单元组合成的结构近似代替原来的连续结构。
如果能合理地求得各单元的力学特性,也就可以求出组合结构的力学特性。
于是,该结构在一定的约束条件下,在给定的载荷作用下,各节点的位移即可以求得,进而求出单元内的其他物理场量。
这就是有限元方法直观的物理的解释。
从数学角度理解,是将图7-1所示的求解区域剖分成许多三角形子区域,子域内的位移可以由相应各节点的待定位移合理插值来表示。
根据原问题的控制方程(如最小势能原理)和约束条件,可以求解出各节点的待定位移,进而求得其他场量。
推广到其他连续域问题,节点未知量也可以是压力、温度、速度等物理量。
这就是有限元方法的数学解释。
从有限元法的解释可得,有限元法的实质就是将一个无限的连续体,理想化为有限个单元的组合体,使复杂问题简化为适合于数值解法的结构型问题;且在一定的条件下,问题简化后求得的近似解能够趋近于真实解。
有限元分析计算实例11.1例题1 受扭矩作用的圆筒11.1-1划分四面体网格的计算(1)进入【零部件设计】工作台启动软件。
单击【开始】→【机械设计】→【零部件设计】选项,如图11-1所示,进入【零部件设计】工作台。
图11-1 单击【开始】→【机械设计】→【零部件设计】选项单击后弹出【新建零部件】对话框,如图11-2所示。
在对话框内输入新的零件名称,在本例题中,使用默认的零件名称【1】。
点击对话框内的【确定】按钮,关闭对话框,进入【零部件设计】工作台。
(2)进入【草图绘制器】工作台在左边的模型树中单击选中【平面】, 如图11-3所示。
单击【草图编辑器】工具栏内的【草图】按钮,如图11-4所示。
这时进入【草图绘制器】工作台。
图11-2 【新建零部件】对话框图11-3 单击选中【平面】(3)绘制两个同心圆草图点击【轮廓】工具栏内的【圆】按钮,如图11-5所示。
在原点点击一点,作为圆草图的圆心位置,然后移动鼠标,绘制一个圆。
用同样分方法再绘制一个同心圆,如图11-6所示。
图11-4 【草图编辑器】工具栏图11-5【轮廓】工具栏下面标注圆的尺寸。
点击【约束】工具栏内的【约束】按钮,如图11-7所示。
点击选择圆,就标注出圆的直径尺寸。
用同样分方法标注另外一个圆的直径,如图11-8所示。
图11-6 两个同心圆草图图11-7 【约束】工具栏双击一个尺寸线,弹出【约束定义】对话框,如图11-9所示。
在【直径】数值栏内输入100,点击对话框内的【确定】按钮,关闭对话框,同时圆的直径尺寸被修改为100。
用同样的方法修改第二个圆的直径尺寸为50。
修改尺寸后的圆如图11-10所示。
图11-8 标注直径尺寸的圆草图图11-9 【约束定义】对话框(4)离开【草图绘制器】工作台点击【工作台】工具栏内的【退出工作台】按钮,如图11-11所示。
退出【草图绘制器】工作台,进入【零部件设计】工作台。
图11-10 修改直径尺寸后的圆图11-11【工作台】工具栏(5)拉伸创建圆筒点击【基于草图的特征】工具栏内的【凸台】按钮,如图11-12所示。