函数的间断点
- 格式:docx
- 大小:158.65 KB
- 文档页数:6



间断点怎么求•首先我们要知道找函数间断点的方法,这里有几种情况。
1.找到函数f(x)在定义域内无定义的1.找“疑似点”,比如分段函数,绝对值函数端点,并求出该处的极限值若极限不存在,则该点必为间断点若极限存在,但不等于函数值,则该点也必为间断点2求间断点处的左右极限,并结合间断点定义,做出判断是哪种类型的间断点注意:此种方法的好处在于“没有多余计算”,因为在第一步的过程中,你已经过滤掉了- -些类型的间断点了,过滤后剩下的无定义点和“疑似点”都是只是差左右极限未求,在第二步统一求出,即可判断出间断点的类型。
3间断点分为可去间断点、跳跃间断点、无穷间断点、震荡间断点。
这是例题分析。
如果函数f(x)有下列情形之一:(1)函数f(x)在点x0的左右极限都存在但不相等,即f(x0+)≠f(x0-);(2)函数f(x)在点x0的左右极限中至少有一个不存在;(3)函数f(x)在点x0的左右极限都存在且相等,但不等于f(x0)或者f(x)在点x0无定义。
则函数f(x)在点x0为不连续,而点x0称为函数f(x)的间断点。
扩展资料:间断点的分类:1、可去间断点:函数在该点左极限、右极限存在且相等,但不等于该点函数值或函数在该点无定义。
如函数y=(x^2-1)/(x-1)在点x=1处。
2、跳跃间断点:函数在该点左极限、右极限存在,但不相等。
如函数y=|x|/x在点x=0处。
3、无穷间断点:函数在该点可以无定义,且左极限、右极限至少有一个不存在,且函数在该点极限为∞。
如函数y=tanx在点x=π/2处。
4、振荡间断点:函数在该点可以无定义,当自变量趋于该点时,函数值在两个常数间变动无限多次。
如函数y=sin(1/x)在x=0处。
可去间断点和跳跃间断点称为第一类间断点,也叫有限型间断点。
其它间断点称为第二类间断点。

函数的间断点
函数的间断点(Intersection of Functions)是指两个函数的值(y的值)相等时的x的值。
它代表着两个函数的交点。
1. 定义:
函数的间断点是指在两个函数的图形交点处的横坐标值,在数学上表示为f(x) = g(x),即两个函数f(x)和g(x)在某一点处具有相同的y值。
2. 示例:
以下是两个函数f(x) 和g(x) 例子:
f(x) = x2 + 2x – 3
g(x) = x2 - 2
现求解以上函数的间断点即x的值:
先将f(x)和g(x)化简后得到:
f(x) = x2 - 2x + 3
g(x) = x2 - 2
令 f(x) = g(x) 得
x2 - 2x + 3 = x2 - 2
解得 x = 1
因此这两个函数的间断点x的值为1.
3. 关系:
间断点处的x值表明了两个函数连接起来后的形状和拐点,即可以通
过函数的间断点判断两个函数的大致连接状态。
4. 应用:
函数的间断点在数学中有着广泛的应用,例如在描绘函数图像及求极
值时常会用到这种技巧;也可以应用到力学,物理学以及热力学领域。
5. 计算:
常见的函数有线性函数和非线性函数。
计算两个函数的间断点的方法
也不同,一般情况下:
(1)线性函数的求解:线性函数的求解较为容易,只需要令两个相等,然后解出x的值即可。
(2)非线性函数的求解:非线性函数求解可以通过数值求解法,例如矩阵法、牛顿迭代求解和拟牛顿求解等方法,以及图像法。


函数间断点的相关知识
在数学中,函数间断点指的是函数在某些点上不连续的情况。
间断点可以分为几种不同类型,其中一些主要的类型包括:
1.第一类间断点(第一类不可去间断点):在这种情况下,函数在间断点处的极限值不存在。
这可能是由于函数在该点没有定义,或者在该点的左右极限值不相等。
2.第二类间断点(第一类可去间断点):在这种情况下,函数在间断点处的极限值存在,但函数在该点的函数值未定义或与极限值不相等。
这种情况通常可以通过对函数进行修正或重新定义来解决。
3.跳跃间断点:函数在跳跃间断点处的左右极限值存在,但它们不相等。
这导致了函数值的突然“跳跃”。
4.可去间断点:这是指函数在某一点的函数值未定义,但可以通过对该点进行修正或重新定义,使得函数在该点变得连续。
5.无穷间断点:在这种情况下,函数在某点的极限值为正无穷或负无穷,导致函数在该点处不连续。
在分析函数间断点时,可以使用极限的概念来进一步理解函数在特定点的行为。
函数的间断点可能对于理解函数的性质、图形和应用有重要意义。
在实际问题中,了解函数的间断点有助于更好地理解函数的行为和性质。


函数间断点及类型
函数间断点指的是函数在某些点上失去连续性的现象。
一般来说,这种现象可能由以下几种情况引起:
1. 可去间断点:在该点上,函数存在极限值,但不连续。
2. 跳跃间断点:在该点上,左右极限值不等。
3. 本质间断点:在该点上,函数既不存在极限值,也不连续。
对于这些不同类型的间断点,我们可以通过不同的方法来判断它们的性质和特点。
比如,对于可去间断点,我们可以通过极限值来确定它的性质;而对于跳跃间断点和本质间断点,则需要通过左右极限值的大小比较和函数的形态来判断它们的性质。

函数间断点的分类及判断方法在一般的函数中,当函数的值突然变化时,就会出现间断点。
间断点也被称为函数的变曲点、拐点、变点、控制点,指的是一类特殊的点。
在具体的运算中,都把它们作为矩阵的某种特征考虑进来,使矩阵更加规范。
这里给大家介绍函数间断点的分类及判断方法,希望能帮助大家对其有更多的了解。
一、函数间断点的分类1、极值点极值点是一种比较常见的函数间断点,它指的是函数增加或减少最快的点,即函数单调性切换的地方,且这个点的曲率为0。
函数在极值点处有最大值或最小值,也可以有驻点,这种函数的驻点的做法为:在该函数的图像上,正负不变,其值也不变,叫做驻点。
2、拐点拐点也称为变曲点,它指的是把一曲线的本来的曲率发生变化的点。
它的主要特征就是曲率由负值变为正值或者曲率由正值变为负值,即由弯曲变为直线或者由直线变为弯曲,这时函数在拐点处不可能有极值。
3、切点切点是一种常见的函数间断点,它指的是曲线在两个相邻的点间的切线平行的点。
在曲线的的切点处,函数的斜率必须要等于切线的斜率。
而且切点也不可能有极值,但是可能有驻点。
4、驻点驻点指的是函数在该点处的曲率和函数值都不变,而且函数在该点处也不会出现极值。
二、函数间断点的判断方法1、把函数表示为链式法则首先把函数表示为一组链式法则,这样便可以快速的确定其在任意点的导数及其极值情况,而在计算导数为零的点的时候,就可以得到关于函数拐点的信息了。
2、判断极值点可以把函数的斜率表示出来,然后判断极值点,使用链式法则来计算函数的斜率,当函数的斜率为0时,说明此处为极值点,从而可以判断出函数的极值点。
3、判断拐点可以把函数的二阶导数表示出来,然后判断拐点。
二阶导数可以用来表示曲线的曲率,函数的二阶导数为0时,表明此处为拐点,从而可以得到函数的拐点。
4、判断切点切点可以把函数的一阶导数表示出来,然后判断切点。
一阶导数可以用来表示曲线的斜率,而函数的一阶导数为0时,表明此处为切点,从而可以得到函数的切点。

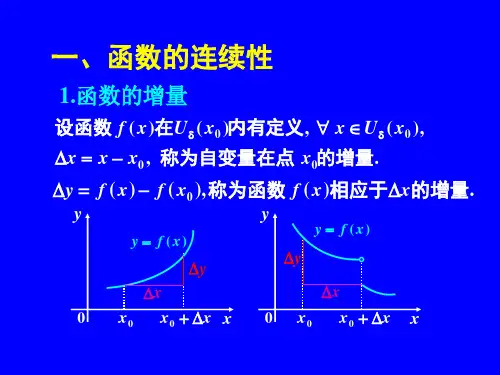
第七讲 函数的间断点重点:分段函数函数在分界点x 0处间断的判定。
难点:函数的间断点的判定。
函数的间断点如果函数)(x f 在点0x 处不连续,则称)(x f 在点0x 处间断,点0x 叫做)(x f 的间断点。
函数在点0x 处连续,必须同时满足三个条件: (1)在点0x 及其附近有定义;(2)极限)(limx f x x →存在; (3))()(lim00x f x f x x =→。
如果上述三个条件中至少有一个条件不满足,则点0x 叫是函数)(x f 的间断点。
如何寻找函数的间断点?一般来说,初等函数无意义的点是间断点;分段函数的分段点可能是间断点。
例2 讨论函数12)(2--+=x x xx f 在1=x点处的连续性。
解 因为函数12)(2--+=x x xx f 在1=x点没有定义,故此函数在1=x 处不连续。
所以,1=x是函数的间断点。
)(lim 1x f x →=3,如果补充定义:令3)1(=f ,则所给函数在1=x处连续。
所以1=x称为该函数的可去间断点。
例 3 讨论函数xx f 1sin)(=在=x 点处的连续性。
解 因为函数xx f 1sin)(=在=x 点无定义;当x →0时,函数值在-1与1之间振荡(图),所以点=x 称为函数xx f 1sin)(=的振荡间断点。
图1-17例4 判断函数⎩⎨⎧<≥-+=00,1,1)(x x x x x f 在0=x点处的连续性。
解 显然函数⎩⎨⎧<≥-+=00,1,1)(x x x x x f 在点=x 及其附近有定义,又)(limx f x -→=1)1(lim 0-=--→x x)(limx f x +→=1)1(lim 0=++→x x 。
所以,)(limx f x →不存在。
因函数)(x f y=的图形在0=x处产生跳跃现象,我们称0=x为函数)(x f 跳跃间断点。
例5 判断函数⎪⎩⎪⎨⎧=≠=0,10,1sin )(x x xx x f 在点0=x处的连续性。
函数间断点知识笔记间断点的条件:设函数()f x 在点0x 的某去心邻域内有定义,在此前提下,如果函数()f x 有下列三种情形之一:(1) 在0x x 没有定义(2) 在0x x 有定义,但0lim ()x x f x 不存在 (3) 在0x x 有定义,0lim ()x x f x 存在,但00lim ()()x x f x f x 那么函数()f x 在点0x 不连续,而点0x 称为函数()f x 的不连续点或间断点无穷间断点:()tan()f x x()tan()f x x 在2x 无定义,且2lim tan()x x 震荡间断点:1()sin()f x x1()sin(f x x在点0x 没有定义,当0x 时,函数值在1 和-1之间变动无限多次 可去间断点:(图不是很好看)21()1x f x x 21()1x f x x 在点1x 没有定义,但在这里有2111lim =lim(1)21x x x x x 如果补充定义:令(1)2f 那么函数在点1x 成为连续,这种情况间断点为可去间断点 同例有函数:,1,()1, 1.2x x f x x ,这里就不论述了. 跳跃间断点:1,0,()0,0,1,0.x x f x x x x当0x 时,0000lim ()lim (1)1lim ()lim (1)1x x x x f x x f x x左右极限都存在但不相等,故0lim ()x f x 不存在,因图像在0x 处产生跳跃现象,该类间断点成为跳跃间断点第一类间断点:左极限0()f x 和0()f x 都存在的间断点(跳跃间断点和可去间断点)第二类间断点:非第一类间断点的所有间断点.(无穷间断点和震荡间断点)。
函数的间断点名词解释
函数的间断点是指函数在定义域内某一点处不连续的现象。
当函数在某一点的左右两侧的函数值存在差异,或者函数在该点处无定义,都可以称之为间断点。
函数的间断点可以分为三种类型:可去间断点、跳跃间断点和无穷间断点。
1. 可去间断点:当函数在某一点的左右两侧的函数值存在差异,但可以通过定义函数在该点处的函数值,使得函数在该点处连续。
这种情况下,该点被称为可去间断点。
2. 跳跃间断点:当函数在某一点的左右两侧的函数值存在差异,且无法通过定义函数在该点处的函数值使得函数在该点处连续。
这种情况下,该点被称为跳跃间断点。
3. 无穷间断点:当函数在某一点处趋于无穷大或无穷小,使得函数在该点处无定义,即函数在该点处不存在。
这种情况下,该点被称为无穷间断点。
函数的间断点在数学中具有重要意义,它可以帮助我们研究函数的性质和行为。
通过分析函数的间断点,可以得到函数图像的特点,进而推导出函数的极限、导数等相关概念。
在实际问题中,函数的间断点也常常与物理、经济等领域的现象相联系。
在解析函数的间断点时,需要注意函数的定义域和函数表达式的特点。
有时候,间断点可能是由于定义域的限制导致的,也可能是由于函数表达式的特性造成的。
因此,在分析函数的间断点时,需要全面考虑函数的定义域和函数表达式的特点,以便准确判断函数是否存在间断点,以及间断点的类型。
函数间断点求法两个基本步骤1、间断点(不连续点)的判断在做间断点的题目时,首要任务是将间断点的定义熟记于心。
下面我们一起看一下教材上间断点的定义:2、间断点类型的判断找出函数的间断点后,然后判断间断点的类型,主要通过间断点的左右极限情况来划分:(1)第一类间断点:在间断点处的左右极限都存在.可以分为以下两种:①可去间断点:左右极限存在且相等;②跳跃间断点:左右极限存在但不相等.(2)第二类间断点:在间断点处的极限至少有一个不存在.经常使用到的,有以下两种形式的第二类间断点:①无穷间断点:在间断点的极限为无穷大.②振荡间断点:在间断点的极限不稳定存在. ▪间断点:x 0是f(x)的间断点,f(x)在x 0点处的左右极限都存在为第一类间断点. f(x)在x 0点处左右极限至少有一个不存在,则x 0是f(x)的第二类间断点. 第一类间断点中{可去间断点 : 左右极限相等 跳跃间断点:左右极限不相等第二类间断点:无穷间断点,振荡间断点等.下面通过一道具体的真题,说明函数间断点的求法:函数的间断点一、函数的间断点设函数()x f 在点0x 的某去心邻域内有定义.在此前提下,如果函数()x f 有下列三种情形之一:1.在0x x =没有定义;2.虽在0x x =有定义,但()x f x x 0lim →不存在;y在 间断 x 1⑤ 11-=x y 。
,∞=-=→11lim11x x x 3.虽在0x x =有定义,且()x f x x 0lim →存在,但()()00lim x f x f x x ≠→;则函数()x f 在点0x 为不连续,而点0x 称为函数()x f 的不连续点或间断点.下面我们来观察下述几个函数的曲线在1=x 点的情况,给出间断点的分类:在1=x 连续. 在1=x 间断,1→x 极限为2.在1=x 间断,1→x 极限为2. 在1=x 间断,1→x 左极限为2,右极限为1.在0=x 间断,0→x 极限不存在. 像②③④这样在0x 点左右极限都存在的间断,称为第一类间断,其中极限存在的②③称作第一类间断的可补间断,此时只要令()21=y ,则在1=x 函数就变成连续的了;④被称作第一类间断中的跳跃间断.⑤⑥被称作第二类间断,其中⑤也称作无穷间断,而⑥称作震荡间断.就一般情况而言,通常把间断点分成两类:如果0x 是函数()x f 的间断点,但左极限y x 1121-① 1+=x y y x 1121-②112-+=x x y ③ ⎩⎨⎧≥<+=1111x x x y ,,y x 1121-④ ⎩⎨⎧≥<+=111x x x x y ,,yx 1121-⑥ x y 1sin =()00-x f 及右极限()00+x f 都存在,那么0x 称为函数()x f 的第一类间断点.不是第一类间断点的任何间断点,称为第二类间断点.在第一类间断点中,左、右极限相等者称为可去间断点,不相等者称为跳跃间断点.无穷间断点和振荡间断点显然是第二类间断点.例1 确定a 、b 使在处连续.解:在处连续因为;;所以时,在处连续.例2 求下列函数的间断点并进行分类1、分析:函数在处没有定义,所以考察该点的极限.解:因为 ,但在处没有定义 所以 是第一类可去间断点.2、分析:是分段函数的分段点,考察该点的极限.解:因为 ,而所以 是第一类可去间断点.总结:只要改变或重新定义在处的值,使它等于,就可使函数在可去间断点处连续.3、分析:是分段函数的分段点,且分段点左右两侧表达式不同,考察该点的左、右极限.⎪⎪⎩⎪⎪⎨⎧>+=<=0,1sin 0,0,sin )(x b x x x a x xxx f 0=x )(x f 0=x )(lim 0x f x +→⇔)(lim 0x f x -→=)0(f =b b x x x f x x =⎪⎭⎫⎝⎛+=++→→1sin lim )(lim 001sin lim )(lim 00==--→→x x x f x x a f =)0(1==b a )(x f 0=x 11)(2+-=x x x f 1-=x 2)1(lim 11lim 121-=-=+--→-→x x x x x )(x f 1-=x 1-=x ⎪⎩⎪⎨⎧=≠=.0,1,0,1sin )(x x xx x f 0=x 01sin lim 0=→x x x 1)0(=f 0=x )(x f 0x )(lim 0x f x x →0x ⎩⎨⎧<-≥+=.0,1,0,1)(x x x x x f 0=x解:因为;所以 是第一类跳跃间断点.4、分析:函数在处没有定义,且左、右极限不同,所以考察该点的单侧极限.解:因为 ; 所以 是第一类跳跃间断点.5、解:因为所以 是第二类无穷间断点6、解:极限不存在所以 是第二类振荡间断点7、求的间断点,并将其分类. 解:间断点:当时,因,故是可去间断点.当时,因,故是无穷间断点.小结与思考:本节介绍了函数的连续性,间断点的分类.1、求分析:通过极限运算,得到一个关于x 的函数,找出分段点,判断.1)1(lim )(lim 00=+=++→→x x f x x 1)1(lim )(lim 0-=-=--→→x x f x x 0=x x x f 1arctan)(=0=x 21arctan lim )(lim 00π==++→→x x f x x 21arctan lim )(lim 00π-==--→→x x f x x 0=x xe xf 1)(=+∞==++→→xx x e x f 100lim )(lim 0=x x x f 1sin)(=x x f x x 1sinlim )(lim 0→→=0=x x xx f sin )(=),2,1,0( ±±==k k x π0=x 1sin lim0=→x xx 0=x ),2,1( ±±==k k x π∞=→x x k x sin lim π),2,1( ±±==k k x πnn x xx f 211lim)(++=∞→解:因为;所以是第一类跳跃间断点 因为;;所以是连续点.⎪⎪⎩⎪⎪⎨⎧-==><<-+=.1,01,11,011,1)(x x x x x x f 00lim )(lim 11==++→→x x x f 2)1(lim )(lim 11=+=--→→x x f x x 1=x 0)1(lim )(lim 11=+=++-→-→x x f x x 00lim )(lim 11==---→-→x x x f 0)1(=-f 1-=x。
函数的间断点的定义可去间断点是指在特定点的函数存在极限,但由于函数在该点未定义或定义与极限值不相等,造成函数在该点的间断。
可去间断点可能是由于函数的定义域中缺失一些点,导致函数在这些缺失的点上没有定义;也可能是由于一些点上函数的值与函数在该点的极限值不相等。
举个例子来说明可去间断点的情况,考虑函数f(x)=(x-1)/(x-1)。
这个函数在定义域中除去x=1这个点时,可以简化为f(x)=1、然而,在x=1这个点上,函数的定义为0/0,没有确定的值。
所以函数在x=1处存在可去间断点。
跳跃间断点是指函数在特定点的左右极限存在,但两个极限值不相等,即函数的值在该点出现了突变的情况。
这种情况通常是由于函数在该点存在一个孤立点或不连续点,导致函数的极限值发生了跃变。
举个例子来说明跳跃间断点的情况,考虑函数 g(x) = floor(x)(即取整函数,将 x 向下取整),这个函数在整数点上的左右极限分别为(n-1, n) ,其中 n 为整数。
由于这个函数在整数点上存在突变,函数在整数点上存在跳跃间断点。
无穷间断点是指函数在特定点的极限值为正无穷或负无穷的情况。
这种情况通常是由于函数在该点附近发散或趋近于无穷大或无穷小的情况。
举个例子来说明无穷间断点的情况,考虑函数h(x)=1/x。
这个函数在x=0处的右极限为正无穷,而左极限为负无穷,所以函数在x=0处存在无穷间断点。
总之,函数的间断点反映了函数图像在特定点或一些点的不连续性,它可以是可去间断点、跳跃间断点或无穷间断点。
对于函数的研究和分析,了解间断点的性质和位置十分重要,它们可以帮助我们更好地理解函数的特性和行为。
函数间断点求法两个基本步骤
1、间断点(不连续点)的判断
在做间断点的题目时,首要任务是将间断点的定义熟记于心。
下面我们一起看一下教材上间断点的定义:
2、间断点类型的判断
找出函数的间断点后,然后判断间断点的类型,主要通过间断点的左右极限情况来划分:
(1)第一类间断点:在间断点处的左右极限都存在.可以分为以下两种:
①可去间断点:左右极限存在且相等;
②跳跃间断点:左右极限存在但不相等.
(2)第二类间断点:在间断点处的极限至少有一个不存在.经常使用到的,有以下两种形式的第二类间断点:
①无穷间断点:在间断点的极限为无穷大.
②振荡间断点:在间断点的极限不稳定存在. ▪间断点:
x 0是f(x)的间断点,f(x)在x 0点处的左右极限都存在为第一类间断点. f(x)在x 0点处左右极限至少有一个不存在,则x 0是f(x)的第二类间断点. 第一类间断点中{
可去间断点 : 左右极限相等 跳跃间断点:左右极限不相等
第二类间断点:无穷间断点,振荡间断点等.
下面通过一道具体的真题,说明函数间断点的求法:
函数的间断点
一、函数的间断点
设函数()x f 在点0x 的某去心邻域内有定义.在此前提下,如果函数()x f 有下列三种情形之一:
1.在0x x =没有定义;
2.虽在0x x =有定义,但()x f x x 0
lim →不存在;
y
在 间断 x 1
⑤ 1
1-=x y 。
,∞=-=→1
1
lim
11
x x x 3.虽在0x x =有定义,且()x f x x 0
lim →存在,但()()00
lim x f x f x x ≠→;
则函数()x f 在点0x 为不连续,而点0x 称为函数()x f 的不连续点或间断点.
下面我们来观察下述几个函数的曲线在1=x 点的情况,给出间断点的分类:
在1=x 连续. 在1=x 间断,1→x 极限为2.
在1=x 间断,1→x 极限为2. 在1=x 间断,
1→x 左极限为2,右极限为1.
在0=x 间断,0→x 极限不存在. 像②③④这样在0x 点左右极限都存在的间断,称为第一类间断,其中极限存在的②③称作第一类间断的可补间断,此时只要令()21=y ,则在1=x 函数就变成连续的了;
④被称作第一类间断中的跳跃间断.⑤⑥被称作第二类间断,其中⑤也称作无穷间断,而⑥
称作震荡间断.
就一般情况而言,通常把间断点分成两类:如果0x 是函数()x f 的间断点,但左极限
y x 1121-① 1+=x y y x 11
21-②
11
2-+=x x y ③ ⎩⎨⎧≥<+=1111x x x y ,,y x 1121-④ ⎩⎨⎧≥<+=1
1
1x x x x y ,,y
x 1121-⑥ x y 1sin =
()00-x f 及右极限()00+x f 都存在,那么0x 称为函数()x f 的第一类间断点.不是第一类
间断点的任何间断点,称为第二类间断点.在第一类间断点中,左、右极限相等者称为可去间断点,不相等者称为跳跃间断点.无穷间断点和振荡间断点显然是第二类间断点.
例1 确定a 、b 使在处连续.
解:在处连续
因为;;
所以时,
在处连续.
例2 求下列函数的间断点并进行分类
1、
分析:函数在处没有定义,所以考察该点的极限.
解:因为 ,但
在处没有定义 所以 是第一类可去间断点.
2、
分析:是分段函数的分段点,考察该点的极限.
解:因为 ,而
所以 是第一类可去间断点.
总结:只要改变或重新定义在处的值,使它等于,就可使函数在可去间
断点
处连续.
3、
分析:是分段函数的分段点,且分段点左右两侧表达式不同,考察该点的左、右极限.
⎪⎪⎩⎪⎪⎨⎧>+=<=0
,1
sin 0
,0,sin )(x b x x x a x x
x
x f 0=x )(x f 0=x )(lim 0x f x +→⇔)(lim 0x f x -→=)0(f =b b x x x f x x =⎪⎭⎫
⎝⎛+=++→→1sin lim )(lim 001
sin lim )(lim 00==--→→x x x f x x a f =)0(1==b a )(x f 0=x 11
)(2+-=
x x x f 1-=x 2
)1(lim 11lim 1
21-=-=+--→-→x x x x x )(x f 1-=x 1-=x ⎪⎩⎪
⎨⎧
=≠=.0,1,0,1sin )(x x x
x x f 0=x 0
1
sin lim 0=→x x x 1)0(=f 0=x )(x f 0x )(lim 0
x f x x →0
x ⎩⎨
⎧<-≥+=.0,1,0,1)(x x x x x f 0=x
解:因为
;
所以 是第一类跳跃间断点.
4、
分析:函数在处没有定义,且左、右极限不同,所以考察该点的单侧极限.
解:因为 ; 所以 是第一类跳跃间断点.
5、
解:因为
所以 是第二类无穷间断点
6、
解:
极限不存在
所以 是第二类振荡间断点
7、求
的间断点,并将其分类. 解:间断点:
当时,因,故是可去间断点.
当时,因,故
是无穷间断点.
小结与思考:
本节介绍了函数的连续性,间断点的分类.
1、求
分析:通过极限运算,得到一个关于x 的函数,找出分段点,判断.
1
)1(lim )(lim 0
0=+=++
→→x x f x x 1
)1(lim )(lim 0
-=-=--
→→x x f x x 0=x x x f 1arctan
)(=0=x 21arctan lim )(lim 00
π==++→→x x f x x 21arctan lim )(lim 00π
-
==--→→x x f x x 0=x x
e x
f 1
)(=+∞
==++
→→x
x x e x f 10
0lim )(lim 0=x x x f 1sin
)(=x x f x x 1
sin
lim )(lim 0
→→=0=x x x
x f sin )(=
),2,1,0( ±±==k k x π0=x 1
sin lim
0=→x x
x 0=x ),2,1( ±±==k k x π∞
=→x x k x sin lim π),2,1( ±±==k k x πn
n x x
x f 211lim
)(++=∞→
解:因为;
所以是第一类跳跃间断点 因为;;
所以是连续点.
⎪⎪⎩
⎪⎪⎨
⎧-==><<-+=.
1,
01,11,011,1)(x x x x x x f 0
0lim )(lim 1
1
==++
→→x x x f 2
)1(lim )(lim 1
1=+=--
→→x x f x x 1=x 0
)1(lim )(lim 1
1
=+=++-→-→x x f x x 0
0lim )(lim 1
1
==---→-→x x x f 0)1(=-f 1-=x。