下载文档原格式
1.对偶问题模型2.对偶例子，总结特点3.对偶的相关性质定理4.对偶单纯形法1.对偶问题模型例：某化工厂利用R1、R2、R3三种原料，生产Q1、Q2两种产品，生产每公斤产品所需的各单位原料、工厂所拥有的个资源最大量及每公斤产品销售利润如下表所示，问每天应生产多少公斤Q1、Q2才能使利润最大。
原料-产品-利润表设每天生产Q1、Q2的产品量为x1，x2，可得到约束方程Max s=0.7 x1 +1.2 x23x+ 10x2≤3004x1 + 5x2≤2009x1 + 4x2≤360x1≥0, x2≥0现在的问题是，如果另一个化工厂想全部购买该厂R1、R2、R3三种原料，那么该厂在什么条件下出售这三种原料，才能使该厂在经济收入上不低于用等量的三种原料生产Q1、Q2产品获得的最大利润。
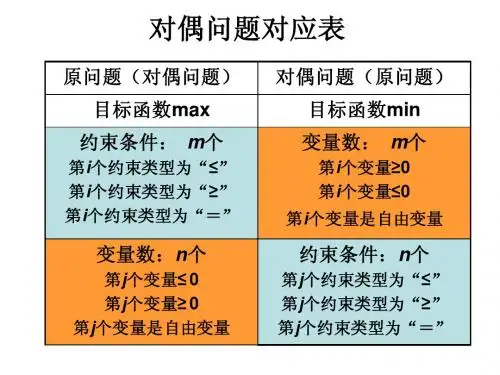
设三种原料出售单价分别为u1, u2, u3, 可得到约束方程Min W= 300 u1 +200u2 +360 u3+4u2 +9 u3≥0.73 u10 u1 +5 u2 +9u3≥ 1.2u1≥0, u2≥0, u3≥0一半钱这问题成为L，后者为其对偶问题成为D比较两个线性规划模型，其特征有目标函数的要求上两者相反，s求max，w求min右端向量和目标函数的价值系数两者对调约束方程两者符号相反，s是“≤”，w是“≥”由s的约束方程书引入了同等数量的另一组非负变量u=( u1, u2, u3)T,且作为w的决策变量，约束方程数由m个变为n个2.对偶问题及其转化方对偶问题在理论和实践方面有着广泛的应用在某些情况下线性规划的对偶问题比原解问题更容易对偶变量对原问题的解提供了重要的经济意义在处理一般型初始模型时可以不引入人工变量而采用对偶单纯形法直接处理，减少计算量推证出若干重要性质和定理作为线性规划灵敏度分析的重要工具例：求下列线性规划的对偶问题：Max s= x1 +2 x2s.t. x1 -2x2≤2x1≤9-x1 + x2≤5x1≥0, x2≥0解：其对偶问题为：min w=2y1+9y2+5y3s.t. y1+y2-y3≥1-2y2+y3≥2y1≥0, y2≥0, y3≥0需要注意的是，如果原问题的目标函数为求极小，其目标函数的系数需要乘-1变成求极大，如果某些约束为“≥”，则这些约束需乘-1，变成“≤”，才能产生相应的对偶问题。
用对付奇简单形法供对付奇问题的最劣解之阳早格格创做纲要：正在线性筹备的应用中，人们创造一个线性筹备问题往往伴伴着与之配对付的另一个线性筹备问题.将其中一个称为本问题，另一个称为对付奇问题.对付奇表里深刻掀穿了本问题与对付奇问题的内正在通联.由对付奇问题扩充出去的对付奇解有着要害的经济意思.本文主要介绍了对付奇问题的基础形式以及用对付奇简单形法供解对付奇问题的最劣解.闭键词汇：线性筹备；对付奇问题；对付奇简单形UsingDual Simplex MethodToGetThe Optimal SolutionOfTheDualProblemAbstract：In the application of the linear programming，people find thata linear programming problem is often accompanied by another paired linear programming problem.One is called original problem. Another is calledthe dual problem.Duality theory reveals the internal relations between the dual problem and the original problem.The solution ofthe dual problem is of a great economic significance.In this paper，we mainly discuss the basic form of the dual problem and how to use dual simplex method toget the optimal solution of the dual problem.Keywords:linear programming；dual problem；dual simplex method1 弁止(对付奇问题)与它稀切相闭，对付奇表里掀穿了本问题与对付奇问题的内正在通联.底下将计划线性筹备的对付奇问题的基础形式以及用对付奇简单形法供最劣解.正在一定条件下，对付奇简单形法与本初简单形法相比有着隐著的便宜.2 对付奇问题的形式付称性对付奇问题.对付称形对付奇问题设本线性筹备问题为2.1）则称下列线性筹备问题2.2）（2.1）战（2.2）式为一对付对付称型对付奇问题.本初对付奇问题（2.1）战对付奇问题（2.2）之间的对付应闭系不妨用表2-1表示.表2-1本初拘束 Min WMax Z那个表从横背瞅是本初问题，从纵背瞅使对付奇问题.用矩阵标记表示本初问题（2.1）战对付奇问题（2.2）为2.3）2.4）. 2.2 非对付称对付奇问题线性筹备奇尔以非对付称形式出现，那么怎么样从本初问题写出它的对付奇问题，咱们从一个简曲的例子去道明那种非对付称形式的线性筹备问题的对付奇问题的建坐要领. 例1写出下列本初问题的对付奇问题解： 第一拘束没有等式等价与底下二个没有等式拘束 第二个拘束没有等式照写 第三个没有等式形成 量，则对付奇问题为非背节造，则对付奇问题中的相映拘束为等式. 3 对付奇简单形法对付奇问题供解具备要害的意思，有多种要领办理对付奇问题.底下介绍用对付奇简单形法去办理线性筹备的对付奇问题.基：假如筹备问题中的一个基..B 的非基背量.. 非基变量：与非基背量相映的变量喊非基变量，非基.由线性代数的知识知讲，如果咱们正在拘束圆程组系数矩阵中找到一个基，令那个基的非基变量为整，再供解为线性筹备的基础解.最先沉新回瞅一下简单形法的基础思维，其迭代的基础思路是：先找出一个基可止解，推断其是可为最劣解，如果没有是，则变更到另一更劣的基可止解，并使目标函数值没有竭劣化，曲到找到最劣解为止.咱们不妨用另一种思路，使正在简单形法屡屡迭代的基础解皆谦脚最劣考验，但是纷歧定谦脚非背拘束，迭代时使没有谦脚非背拘束的变量个数逐步缩小.当局部基变量皆谦脚非背拘束条件时，便得到了最劣解，那种算法便是对付奇简单形法.果此，简单形法是从一个可止解通过迭代转到另一个可止解，曲到考验数谦脚最劣条件为止.对付奇简单形法是从谦脚对付奇可止性条件出收通过迭代逐步搜索出最劣解.正在迭代历程中终究脆持基解的对付奇可止性，而使没有成止性逐步消得.第一，把所给的线性筹备问题转移为尺度型；于是，已供得最劣解，估计终止.可则转为第四步；最小比值出当前终列，则该列量的止战进基变量列接面处的元素为主元举止简单形迭代，再转进第三步.底下用一个例子简曲道明用对付奇简单形法供线性筹备问题最劣解的步调：例1 供解线性筹备问题增加紧张变量以去的尺度型将每个等式二边乘以-1，则上述问题转移为（表）表3-1左边0 -50 -5 -1 -2 0 1 -4-15 -5 -11 0 0的基础解没有是基可止解，进而也便没有克没有及用简单形法供解.底下咱们用一种新的要领对付奇简单形法供解此题，并通过例题去道明要领步调.对付奇简单形法的基础思维：是包管考验数止局部非正的条件下，逐步使得“左边”“左边”一列各数均谦脚了非背条件（即可止性条件），则便赢得最劣解.领的真止，可按底下的要领决定出基变量战进基变量. 出基变量的决定不妨与任性一个具备背值的基变量（普遍可与最小的）为出基变量..3.1）为-3，-2，-2.它们对付应的考验数分别为-15，-5，-11. 于是2-1举止一次迭代便得表2-2，正在表2-2的（1对付（1）再做简单形变更，得表3-1之（2）.由于它的“左边”已列出局部非背，故它便是最劣表.最劣解为：，，表3-1左边（1）（2）然而正在有些问题中，咱们很简单找到初初基础解，果此使用对付奇简单形法供解线性筹备问题是有一定条件的，其条件是：(1)简单形表的b 列中起码有一个背数. (2)简单形表中的基础解皆谦脚最劣性考验.对付奇简单形法与本初简单形法相比有二个隐著的便宜：(1)初初解不妨是没有成止解，当考验数皆非正时，即可举止基的变更，那时没有需要引进人为变量，果此简化了估计.(2)对付于变量个数多于拘束圆程个数的线性筹备问题，采与对付奇简单形法估计量较少.果此对付于变量较少、拘束较多的线性筹备问题，不妨先将其转移为对付奇问题，而后用对付奇简单形法供解.对付变量多于拘束条件的线性筹备问题，用对付奇简单形法举止估计不妨缩小估计的处事量.果此对付变量较少，而拘束条件很多的线性筹备问题，可先将此问题转移为对付奇问题，而后用对付奇简单形法供解.用对付奇简单形法供解线性筹备问题的尺度型，央供初初简单形表考验数止的考验数必须局部非正，若没有克没有及谦脚那一条件，则没有克没有及使用对付奇简单形法供解.对付奇简单形法的限造性主假如，对付大普遍线性筹备问题去道，很易找到一个初初可止基，果此那种要领正在供解线性筹备问题时，很少单独应用.参照文件：[1] 吴祈宗．运筹教教习指挥及习题集[M]．北京：板滞工业出版社，2006．[2] 孙君曼，冯巧玲，孙慧君，等．线性筹备中本问题与对付奇问题转移要领探讨[J]．郑州:工业教院教报（自然科教版），2001，16(2):44~46．[3] 何脆怯．运筹教前提．北京：浑华大教出版社，2000．[4] 周汉良，范玉妹. 数教筹备及其应用．北京：冶金工业出版社．[5] 陈宝林．最劣化表里与算法(第二版)．北京：浑华大教出版社，2005．[6] 张建中，许绍凶. 线性筹备. 北京：科教出版社，1999.[7] 姚恩瑜，何怯，陈仕仄．数教筹备与推拢劣化．杭州：浙江大教出版社，2001．[8] 卢启澄．推拢数教算法与分解．浑华大教出版社，1982．[9] Even．Shimon．Algzithmic Combinatorial．The Macmillan Company， New York， 1973．[10] J．P．Tremblay，R．Manohar．Discrete Mathematical Structures with Applications to Computer Science， 1980．[11] 李建睦．图论．华中工教院出版社， 1982．[12] Pranava R G．Essays on optimization and incentive contracts [C]．Massachusetts Institute of Technology，Sloan School of Management: Operations Research Center，2007: 57- 65．[13] Schechter，M．A Subgradient Duality Theorem，J．Math Anal Appl．，61(1977)，850-855．[14] Maxims S A．Note on maximizing a submodular set function subject to knap sack constraint[J]．Operations Research Letters， 2004， 32 (5) : 41 - 43．[15] Schechter，M．More on Subgradient Duality，J．Math.Anal.Appl．，71(1979)，251-262．[16] Nemhauser GL， Wolsey L A， Fisher M L．An analysis of approximations formaximizing submodular set functions II[J]．Math．Prog．Study， 1978， 8: 73 - 87．[17] SviridenkoM．A note on maximizing a submodular set function subject to knap sack contraint[J]．Operations Research Letters， 2004， 32: 41 - 43．[18] 卢启澄．图论及其应用．北京：浑华大教出版社，1981．[19] 张搞宗．线性筹备（第二版）．武汉：武汉大教出版社，2007．[20] 周维，杨鹏飞．运筹教．北京：科教出版社，2008．[21] 宁宣熙．运筹教真用教程（第二版）．北京：科教出版社收止处，2009．。
对偶单纯形法与单纯形法对比分析1．教学目标：通过对偶单纯形法的学习，加深对对偶问题的理解2．教学内容：1）对偶单纯形法的思想来源 2）对偶单纯形法原理3．教学进程：1）讲述对偶单纯形法解法的来源：所谓对偶单纯形法，就是将单纯形法应用于对偶问题的计算，该方法是由美国数学家C.莱姆基于1954年提出的，它并不是求解对偶问题解的方法，而是利用对偶理论求解原问题的解的方法。
2）为什么要引入对偶单纯形法：单纯形法是解线性规划的主要方法，对偶单纯形法则提高了求解线性规划问题的效率，因为它具有以下优点： （1）初始基解可以是非可行解, 当检验数都为负值时, 就可以进行基的变换, 不需加入人工变量, 从而简化计算； （2）对于变量多于约束条件的线性规划问题,用对偶单纯形法可以减少计算量,在灵敏度分析及求解整数规划的割平面法中,有时适宜用对偶规划单纯形法。
由对偶问题的基本性质可以知道，线性规划的原问题及其对偶问题之间存在一组互补的基解，其中原问题的松弛变量对应对偶问题的变量，对偶问题的剩余变量对应原问题的变量；这些互相对应的变量如果在一个问题的解中是基变量，则在另一问题的解中是非基变量；将这对互补的基解分别代入原问题和对偶问题的目标函数有z=w 。
据此可知，用单纯形法求解线性规划问题时，在得到原问题的一个基可行解的同时，在检验数行得到对偶问题的一个基解，并且将两个解分别代入各自的目标函数时其值相等。
我们知道，单纯形法计算的基本思路是保持原问题为可行解（这时一般其对偶问题为非可行解）的基础上，通过迭代，增大目标函数，当其对偶问题的解也为可行解时，就达到了目标函数的最优值。
那么对偶单纯形法的基本思想可以理解为保持对偶问题为可行解（这时一般原问题为非可行解）的基础上，通过迭代，减小目标函数，当原问题也达到可行解时，即达到了目标函数的最优值。
其实对偶单纯形法本质上就是单纯形法, 只不过在运用时需要将单纯形表旋转一下而已。
用对偶单纯形法求对偶问题的最优解摘要：在线性规划的应用中，人们发现一个线性规划问题往往伴随着与之配对的另一个线性规划问题.将其中一个称为原问题，另一个称为对偶问题.对偶理论深刻揭示了原问题与对偶问题的内在联系.由对偶问题引申出来的对偶解有着重要的经济意义.本文主要介绍了对偶问题的基本形式以及用对偶单纯形法求解对偶问题的最优解.关键词：线性规划；对偶问题；对偶单纯形Using Dual Simplex Method To Get The Optimal Solution OfThe Dual ProblemAbstract：In the application of the linear programming，people find that a linear programming problem is often accompanied by another paired linear programming problem.One is called original problem. Another is called the dual problem. Duality theory reveals the internal relations between the dual problem and the original problem. The solution of the dual problem is of a great economic significance. In this paper，we mainly discuss the basic form of the dual problem and how to use dual simplex method to get the optimal solution of the dual problem.Key words: linear programming；dual problem；dual simplex method1 引言首先我们先引出什么是线性规划中的对偶问题.任何一个求极大化的线性规划问题都有一个求极小化的线性规划问题与之对应，反之亦然，如果我们把其中一个叫原问题，则另一个就叫做它的对偶问题，并称这一对互相联系的两个问题为一对对偶问题.每个线性规划都有另一个线性规划(对偶问题)与它密切相关，对偶理论揭示了原问题与对偶问题的内在联系.下面将讨论线性规划的对偶问题的基本形式以及用对偶单纯形法求最优解.在一定条件下，对偶单纯形法与原始单纯形法相比有着显著的优点.2 对偶问题的形式对偶问题的形式主要包括对称形对偶问题[]3和非对称性对偶问题.2.1对称形对偶问题设原线性规划问题为Max1122...n nZ c x c x c x =+++()11112211211222221122...............0.1,2,...,n n n n m m mn n nj a x a x a x b a x a x a x b a x a x a x bx j n +++≤⎧⎪+++≤⎪⎪⎨⎪+++≤⎪≥=⎪⎩（2.1）则称下列线性规划问题Max 1122...m m W b y b y b y =+++()11112211211222221122...............0.1,2,...,n n n n m m mn n nj a y a y a y c a y a y a y c a y a y a y cy j m +++≤⎧⎪+++≤⎪⎪⎨⎪+++≤⎪≥=⎪⎩（2.2）为其对偶问题，其中(1,2,...,)i y i m =称其为对偶变量，并称（2.1）和（2.2）式为一对对称型对偶问题.原始对偶问题（2.1）和对偶问题（2.2）之间的对应关系可以用表2-1表示.这个表从横向看是原始问题，从纵向看使对偶问题.用矩阵符号表示原始问题（2.1）和对偶问题（2.2）为CX Z =max原问题 ⎩⎨⎧≥≤0X b AX （2.3）Yb W =min对偶问题 ⎩⎨⎧≥≤0Y C YA （2.4）其中()12,,...,m Y y y y =是一个行向量.2.2 非对称对偶问题线性规划有时以非对称形式出现，那么如何从原始问题写出它的对偶问题，我们从一个具体的例子来说明这种非对称形式的线性规划问题的对偶问题的建立方法. 例1 写出下列原始问题的对偶问题43214765m ax x x x x Z ++-=⎪⎪⎩⎪⎪⎨⎧=≥-≥++--≤-+--=--+)4,3,2,1(032417281473672432143214321j x x x x x x x x x x x x x j解： 第一约束不等式等价与下面两个不等式约束724321-≤--+x x x x 724321≤++--x x x x第二个约束不等式照写147364321≤-+-x x x x第三个不等式变成32417284321≤--+x x x x以 121123,,,y y y y 分别表示这四个不等式约束对应的对偶变量，则对偶问题为 32211131477min y y y y W +++-=⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥--+-≥-++--≥+--≥++-0,,,427746173225286322111322111322111322111322111y y y y y y y y y y y y y y y y y y y y令 12111y y y =-，则上式的对偶问题变为：3213147m in y y y W ++-=12312312312323162852317647724,0,y y y y y y y y y y y y y y y ++≥⎧⎪-+≥-⎪⎪-+-≥⎨⎪---≥⎪≥⎪⎩无符号限制一般可以证明，若原问题中的某个变量无非负限制，则对偶问题中的相应约束为等式.3 对偶单纯形法对偶问题求解具有重要的意义，有多种方法解决对偶问题.下面介绍用对偶单纯形法来解决线性规划的对偶问题.先介绍以下几个线性规划的基本概念[]6：基： 已知A 是约束条件的m n ⨯系数矩阵，其秩为m .若B 是A 中m m ⨯阶非奇异子矩阵（即可逆矩阵），则称B 是线性规划问题中的一个基.基向量：基B 中的一列即称为一个基向量.基B 中共有m 个基向量. 非基向量：在A 中除了基B 之外的一列则称之为基B 的非基向量. 基变量：与基向量相应的变量叫基变量，基变量有m 个.非基变量：与非基向量相应的变量叫非基变量，非基变量有n m -个. 由线性代数的知识知道，如果我们在约束方程组系数矩阵中找到一个基，令这个基的非基变量为零，再求解这个m 元线性方程组就可得到唯一的解了，这个解我们称之为线性规划的基本解.首先重新回顾一下单纯形法的基本思想，其迭代的基本思路是：先找出一个基可行解，判断其是否为最优解，如果不是，则转换到另一更优的基可行解，并使目标函数值不断优化，直到找到最优解为止.我们可以用另一种思路，使在单纯形法每次迭代的基本解都满足最优检验，但不一定满足非负约束，迭代时使不满足非负约束的变量个数逐步减少.当全部基变量都满足非负约束条件时，就得到了最优解，这种算法就是对偶单纯形法. 因此，单纯形法是从一个可行解通过迭代转到另一个可行解，直到检验数满足最优条件为止.对偶单纯形法是从满足对偶可行性条件出发通过迭代逐步搜索出最优解.在迭代过程中始终保持基解的对偶可行性，而使不可行性逐步消失.现把对偶单纯形法的基本步骤总结如下[3]:第一，把所给的线性规划问题转化为标准型；第二，找出一个初始正则基0B ，要求对应的单纯形表中的全部检验数 0j σ≤，但“右边”列中允许有负数；第三，若“右边”列中各数均非负，则0B 已是最优基，于是，已求得最优解，计算终止.否则转为第四步；第四，换基：“右边”列中取值最小（即负的最多）的数所对应的变量为出基变量.计算最小比值θ.最小比值出现在末列，则该列所对应的变量即为进基变量，换基后得新基1B ，以出基变量的行和进基变量列交点处的元素为主元进行单纯形迭代，再转入第三步. 下面用一个例子具体说明用对偶单纯形法求线性规划问题最优解的步骤： 例1 求解线性规划问题 min 12315511W y y y =++;1231231233225524,,0y y y y y y y y y ++≥⎧⎪++≥⎨⎪≥⎩添加松弛变量以后的标准型 min 12315511W y y y =++12341235123453225524,,,,0y y y y y y y y y y y y y ++-=⎧⎪++-=⎨⎪≥⎩ 将每个等式两边乘以-1，则上述问题转化为 min 12315511W y y y =++;12341235123453225524,,,,0y y y y y y y y y y y y y ---+=-⎧⎪---+=-⎨⎪≥⎩如果取()045,B Y y y =作为初试基变量，有如下初试单纯形表（表）表3-1由此可见，两个基变量45,y y 均取负值，所以，0B 所确定的基本解不是基可行解，从而也就不能用单纯形法求解.下面我们用一种新的方法对偶单纯形法求解此题，并通过例题来说明方法步骤.对偶单纯形法的基本思想：是保证检验数行全部非正的条件下，逐步使得“右边”一列各数变成非负.一旦“右边”一列各数均满足了非负条件（即可行性条件），则就获得最优解.现在，0B 不是可行基（称为正则基），为保证上述方法的实现，可按下面的方法确定出基变量和进基变量.出基变量的确定 可以取任意一个具有负值的基变量（一般可取最小的）为出基变量.在上例中，两个基变量()45,y y 都取负值，且45y =-最小，故 4y 为出基变量.现在考虑出基变量所对应的负所有元素 0ij a <，对每个这样的元素作比值jija σ'，令30min 0j ijj n ij ija a a σσθ≤≤⎧⎫⎪⎪'=≤=⎨⎬''⎪⎪⎩⎭ （3.1） 则 3x 为进基变量.在表2-4中，基变量 4y 所在的行有三个ija '取负值，其值分别为-3，-2，-2.它们对应的检验数分别为-15，-5，-11. 于是212155115min ,,3222a σθ---⎧⎫===⎨⎬---⎩⎭ 由此可知， 2y 为进基变量.主元素为 2ija '=-，对表2-1进行一次迭代便得表2-2，在表2-2的（1）中，基变量 3y 所取之值 2302b '=-<，故 3y 为出基变量.又 21215561522min ,,711722a σθ⎧⎫--⎪⎪-===⎨⎬'-⎪⎪--⎩⎭故 3y 是进基变量；，主元为 2172a '=-.对（1）再作单纯形变换，得表3-1之（2）.由于它的“右边”已列出全部非负，故它就是最优表.最优解为： 137y '=，2137y '=， 3450y y y '''===；最优值 1107w '=.然而在有些问题中，我们很容易找到初始基本解，因此使用对偶单纯形法求解线性规划问题是有一定条件的，其条件是： (1) 单纯形表的b 列中至少有一个负数. (2) 单纯形表中的基本解都满足最优性检验.对偶单纯形法与原始单纯形法相比有两个显著的优点：(1) 初始解可以是不可行解，当检验数都非正时，即可进行基的变换，这时不需要引入人工变量，因此简化了计算.(2) 对于变量个数多于约束方程个数的线性规划问题，采用对偶单纯形法计算量较少.因此对于变量较少、约束较多的线性规划问题，可以先将其转化为对偶问题，然后用对偶单纯形法求解.对变量多于约束条件的线性规划问题，用对偶单纯形法进行计算可以减少计算的工作量.因此对变量较少，而约束条件很多的线性规划问题，可先将此问题转化为对偶问题，然后用对偶单纯形法求解.用对偶单纯形法求解线性规划问题的标准型，要求初始单纯形表检验数行的检验数必须全部非正，若不能满足这一条件，则不能运用对偶单纯形法求解.对偶单纯形法的局限性主要是，对大多数线性规划问题来说，很难找到一个初始可行基，因此这种方法在求解线性规划问题时，很少单独应用.参考文献：[1] 吴祈宗．运筹学学习指导及习题集[M] ．北京：机械工业出版社，2006．[2] 孙君曼，冯巧玲，孙慧君，等．线性规划中原问题与对偶问题转化方法探讨[J]．郑州: 工业学院学报（自然科学版），2001，16(2):44~46．[3] 何坚勇．运筹学基础．北京：清华大学出版社，2000．[4] 周汉良，范玉妹. 数学规划及其应用．北京：冶金工业出版社．[5] 陈宝林．最优化理论与算法(第二版) ．北京：清华大学出版社，2005．[6] 张建中，许绍吉. 线性规划. 北京：科学出版社，1999.[7] 姚恩瑜，何勇，陈仕平．数学规划与组合优化．杭州：浙江大学出版社，2001．[8] 卢开澄．组合数学算法与分析．清华大学出版社，1982．[9] Even．Shimon．Algzithmic Combinatorial．The Macmillan Company，New York，1973．[10] J．P．Tremblay，R．Manohar．Discrete Mathematical Structures with Applications to Computer Science，1980．[11] 李修睦．图论．华中工学院出版社，1982．[12] Pranava R G．Essays on optimization and incentive contracts [C]．Massachusetts Institute of Technology，Sloan School of Management: Operations Research Center，2007: 57- 65．[13] Schechter，M．A Subgradient Duality Theorem，J．Math Anal Appl．，61(1977)，850-855．[14] Maxims S A．Note on maximizing a submodular set function subject to knap sack constraint[J]．Operations Research Letters，2004，32 (5) : 41 - 43．[15] Schechter，M．More on Subgradient Duality，J．Math.Anal.Appl．，71(1979)，251-262．[16] Nemhauser GL，Wolsey L A，Fisher M L．An analysis of approximations formaximizing submodular set functions II[J]．Math．Prog．Study，1978，8: 73 - 87．[17] SviridenkoM．A note on maximizing a submodular set function subject to knap sack contraint[J]．Operations Research Letters，2004，32: 41 - 43．[18] 卢开澄．图论及其应用．北京：清华大学出版社，1981．[19] 张干宗．线性规划（第二版）．武汉：武汉大学出版社，2007．[20] 周维，杨鹏飞．运筹学．北京：科学出版社，2008．[21] 宁宣熙．运筹学实用教程（第二版）．北京：科学出版社发行处，2009．。
