八年级数学 相似多边形 同步练习
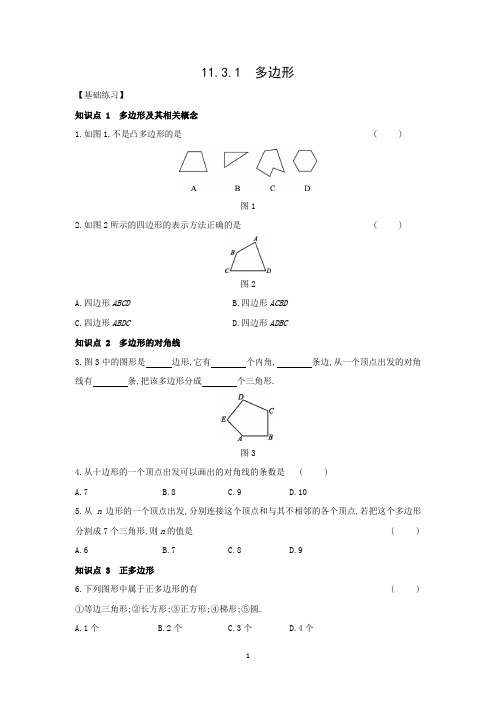
- 格式:doc
- 大小:114.50 KB
- 文档页数:2

§4.4 相似多边形同步练习班级:_______ 姓名:_______一、请你填一填(1)以下五个命题:①所有的正方形都相似②所有的矩形都相似③所有的三角形都相似④所有的等腰直角三角形都相似⑤所有的正五边形都相似.其中正确的命题有_______.(2)已知三个数1,2,3,请你再写一个数,使这四个数能成比例,那么这个数是________(填写一个即可).(3)相同时刻的物高与影长成比例,如果有一根电线杆在地面上的影长是50米,同时高为1.5米的标竿的影长为2.5米,那么这根电线杆的高为________米.(4)在一张比例尺为1∶50000的地图上,量得A、B两地的图上距离为2.5 厘米,那么A、B两地的实际距离是________米.二、如图,图(1)是一个正六边形ABCDEF,使线段BC、FE的长增加相等的数,得图(2),将图(1)中的点A、D分别向两边拉长相等的量,得图(3).那么图(1)与图(2)相似吗?图(1)与图(3)相似吗?图(2)与图(3)呢?为什么?三、(1)如图4—4—1与2—4—2,等腰梯形ABCD与等腰梯形A′B′C′D′相似,∠A′=65°,A′B′=6 cm, AB=8 cm, AD=5 cm,试求梯形ABCD的各角的度数与A′D′、B′C′的长.图4—4—1 图4—4—2(2)如图4—4—3,有一个半径为50米的圆形草坪,现在沿草坪的四周开辟了宽10米的环形跑道,那么:①草坪的外边缘与环形跑道的外边缘所成的两个圆相似吗?②这两个圆的半径之比和周长之比分别是多少?它们有什么关系吗?图4—4—3参考答案§4.4 相似多边形一、(1)①④⑤ (2)23或23或332(填写一个即可) (3)30 (4)1250米二、图(1)与图(2)不相似,图(1)与图(3)不相似,图(2)与图(3)也不相似.理由略三、(1)解:∵等腰梯形ABCD 与A ′B ′C ′D ′相似,∠A ′=65°∴∠A =65°,∠B =65°∠D=∠C=180°-65°=115° 又ADD A AB B A ''='', ∴586D A ''=, ∴A ′D ′=415cm ∴B ′C ′=A ′D ′=415cm (2)解:①两个圆相似②这两个圆的半径分别为50米,60米所以它们的半径之比为5∶6,周长之比为(2π×50)∶(2π×60)即为5∶6,所以这两个圆的半径之比等于周长之比.。

轧东卡州北占业市传业学校4.4 相似多边形一、目标导航1.各角对应相等,各边对应成比例的两个多边形叫做相似多边形;2.相似多边形对应边的比叫做相似比;3.相似多边形的对应边成比例,对应角相等.二、根底过关1.两个矩形一定相似. ( ) 2.两个正方形一定相似. ( ) 3.任意两个菱形都相似. ( ) 4.有一个角相等的两个菱形相似. ( )5.边数不同的多边形一定不相似. ( )三、能力提升;②所有的矩形都相似;③所有的三角形都相似;④所有的等腰直角三角形都相似;7.下面图形是相似形的为( )A.所有矩形 B.所有正方形 C.所有菱形 D.所有平行四边形8.以下说法正确的选项是( )A.所有的三角形都相似 B.所有的正方形都相似C.所有的菱形都相似 D.所有的矩形都相似9.以下四组图形中必相似的是( )A.有一组邻边相等的两个平行四边形 B.有一个角相等的两个等腰梯形C.对角线互相垂直的两个矩形 D.对角线互相垂直且相等的两个四边形.10.以下说法正确的选项是 ( )A.对应边成比例的多边形都相似 B.四个角对应相等的梯形都相似C . 有一个角相等的两个菱形相似D . 有一个锐角相等的两个等腰三角形相似11.四边形ABCD 与四边形A 1B 1C 1D 1相似,相似比为2:3, 四边形A 1B 1C 1D 1与四边形A 2B 2C 2D 2相似,相似比为5:4,那么四边形ABCD 与四边形A 2B 2C 2D 2相似且相似比为( )A . 5:6B . 6:5C . 5:6或6:5D . 8:1512.假设五边形ABCDE∽五边形MNOPQ ,且AB=12,MN=6,AE=7,那么MQ= .13.一个六边形六边长分别为3,4,5,6,7,8,另一个与它相似的六边形的最短边为6,那么其周长为 .14.矩形ABCD 与矩形EFGH 中,AB=4,BC=2,EF=2,FG=1,那么矩形ABCD 与矩形EFGH 相似(填“一定〞或“不一定〞)15.□ABCD 与□ EFGH 中,AB = 4,BC = 2,EF = 2,FG=1,那么□ABCD 与□ EFGH 相似(填“一定〞或“不一定〞)16.把一矩形纸片对折,如果对折后的矩形与原矩形相似,那么原矩形纸片的长与宽之比为 .17.如图,图〔1〕是一个正六边形ABCDEF ,使线段BC 、FE 的长增加相等的数,得图〔2〕,将图〔1〕中的点A 、D 分别向两边拉长相等的量,得图〔3〕.那么图〔1〕与图〔2〕相似吗?图〔1〕与图〔3〕相似吗?图〔2〕与图〔3〕呢?为什么?18.如图,等腰梯形ABCD 与等腰梯形A′B′C′D′相似,∠A′=65°,A′B′=6 cm, AB=8 cm , AD=5 cm ,试求梯形ABCD 的各角的度数与A′D′, B′C′的长.19.如图,矩形ABCD 与矩形EDCF 相似,且CD = 1.求:BC·CF 的值.20.如图,在□ABCD 中,AB//EF ,假设AB = 1,AD = 2,AE=21AB ,那么□ABFE 与□BCDA 相似吗?说明理由. 21.一个矩形剪去一个以宽为边长的正方形后,剩下的矩形与原矩形相似,那么原矩形的长与宽之比为多少?四、聚沙成塔如图, □ABCD 中,EF//AD ,设AB=a ,BC=b ,假设□AEFD ,□EBCF 都与□ABCD 相似,试确定a 与b 之间的关系.4.4相似多边形1.×2.√3.×4.√5.√6.①④⑤;7.B ;8.B ;9.C ;10.C ;11.A ;12.27;13.66;14.一定;15.不一定;16.2;17.都不相似,不符合相似定义;18.各角的度数依次为650,650,1150;1150.B 'C '=A 'D '=415cm ;19.BC·CF=1;20.相似;21.2;22.b 2=2a 2.。

八年级数学下册15.1.1 多边形同步练习(新版)北京课改版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(八年级数学下册15.1.1 多边形同步练习(新版)北京课改版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为八年级数学下册15.1.1 多边形同步练习(新版)北京课改版的全部内容。
15.1。
1多边形一、夯实基础1、把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,那么这张纸片原来的形状不可能是()A.六边形B.五边形C.四边形 D。
三角形2、若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )A.十三边形B.十二边形 C。
十一边形 D.十边形3、在平面内,由一些线段________________相接组成的_____________叫做多边形。
4、连接多边形_________的两个顶点的线段叫做多边形的对角线。
二、能力提升5、若一个多边形共有十四条对角线,则它是( )A.六边形 B。
七边形 C.八边形 D.九边形6、n边形一共有___________条对角线。
7、如果一个多边形的边数恰好是从—个顶点引出的对角线条数的2倍,则此多边形的边数为___________.8、将一个正方形截去一个角,则其边数_________ .9、如图,你能数出多少个不同的四边形?10、下面的两个网格中,每个小正方形的边长均为1 cm,请你分别在每个网格中画出—个顶点在格点上,且周长为12 cm的形状和大小不同的凸多边形。
三、课外拓展11、用两个一样大小的含30°角的三角板可以拼成多少个形状不同的四边形?请画图说明.四、中考链接12、(中考题改编)下列图形中,是正多边形的是()A。

轧东卡州北占业市传业学校 相似多边形的性质一、目标导航1.相似三角形对应高的比,对应角平分线的比和对应中线的比都等于相似比; 2.相似多边形的周长比等于相似比,面积比等于相似比的平方. 二、根底过关1.假设两个相似多边形面积比为9:4,那么它们的周长比是 .2.假设△ABC ∽△A 1B 1C 1,AB=4,BC=5,AC=6,△A 1B 1C 1的最大边长为15,那么它们的相似比是________,△A 1B 1C 1的周长是________.3.两个相似三角形对应角平分线之比为1:4.那么它们的周长比为 ,面积比为 . 4.假设DE 为△ABC 的中位线,且DE//BC ,那么△ADE 与△ABC 的面积比为 . 5.两个相似三角形的相似比为2∶3,它们周长的差是25,那么较大三角形的周长 是________.6.如图,在□ABCD 中,延长AB 到E ,使BE=21AB ,延长CD 到F ,使DF=DC ,EF 交BC 于G ,交AD 于H ,那么△BEG 与△CFG 的面积之比是________.7.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的21倍,那么边长应缩小到原来的________倍. 8.如果两个相似三角形的面积比为9:25,而第一个三角形的周长为36,那么第二个三角形周长是 . 三、能力提升9.把一个矩形纸片ABCD 沿AD 和BC 的中点连线EF 对折,要使矩形AEFB 与原矩形相似,那么原矩形长与宽的比为〔 〕A .2∶1B .3∶1C .2∶1D .4∶110.在△ABC 中,D 、E 分别是边AB 、AC 的中点,△ADE 和四边形BCED 的面积分别记为S 1、S 2,那么21S S 的值为〔 〕 A .21 B .41 C .31 D .32 11.在Rt△ABC 中,AD 为斜边BC 上的高,假设S CAD ∆=3S ABD ∆,那么AB ∶AC 等于〔 〕A .1∶3B .1∶4C .1∶3 D .1∶212.顺次连结三角形三边的中点,所成的三角形与原三角形对应高的比是〔 〕A .1∶4B .1∶3C .1∶2 D .1∶213.如图,DF//EG//BC ,AD=DE=EB ,那么面积比S 1:S 2:S 3等于( )A .1:1:2B .1:3:5C .1:2:3D .1:4:914.如图,假设∠C=900,AD=DB ,ED⊥AB,AB=20,AC=12,那么四边形ADEC 的面积为( )A .75B .58.5C .48D .3715.在梯形ABCD 中,AB//CD ,假设DB ,AC 交于点O ,且△DCO 的面积与△DCB 的面积比为1:3,那么△CDO 与△ABO 的面积比等于( )A .1:9B .1:7C .1:4D .1:5 16.如图,BE//CD ,AB:BC=2:3,那么ECD ABES S ∆∆:=( )A .2:3B .4:15C .4:21D .4:1717.如图,△ABC 是一块锐角三角形余料,其中BC =12 cm ,高AD =8 cm ,现在要把它裁剪成一个正方形材料备用,使正方形的一边在BC 上,其余两个顶点分别在AB 、AC 上,问这个正方形材料的边长是多少?18.如图,在△ABC 中,DE//BC ,EF//AB ,△ADE 和△EFC 的面积分别是4cm 2和9cm 2,求△ABC 的面积. 19.正方形ABCD 中,E 是AC 上一点,EF⊥AB,EG⊥AD,AB =6,AE:EC = 2:1.求四边形AFEG 的面积.20.如图,□ABCD 中,M 为BC 中点,AN=3MN ,BN 的延长线交AC 于E ,交CD 于F .⑴求AE:EC 的值;⑵当S AEB ∆=9时,求S ECF ∆.21.如图, △ABC 中,AB=4,D 在AB 边上移动(不与A ,B 重合),DE//BC 交AC 于E ,连结CD ,设S S ABC=∆,1S S DEC =∆.⑴当D 为AB 中点时,求S S :1的值;⑵假设AD=x ,y SS =1,求y 关于x 的函数关系式及自变量的取值范围. 四、聚沙成塔HF ED C B A GFEDCBA22.如图,梯形ABCD 中,AD//BC ,CE 平分∠BCD,且CE⊥AB 于E ,43=EB AE ,BCE S ∆=14cm 2.求四边形ADCE 的面积.23.△ABC 中,AB=AC=10,BC=12,动点D 在边AB 上,DE⊥AB,点E 在BC 上,点F 在边AC 上,且∠DEF=∠B,当点D在AB 上运动时,⑴FCE S ∆可能等于EBD S ∆的二倍吗?假设可能,请求出BD 的长;假设不可能,请说明理由.⑵FCE S ∆可能等于EBD S ∆的四倍吗?假设可能,请求出BD 的长;假设不可能,请说明理由.24.在Rt△ABC 中, ∠C=900,AC=3,BC=4,点E 在直角边AC 上(点E 与A ,C 两点均不重合),点F 在斜边AB 上(点F 与A ,B 均不重合).⑴假设EF 平分Rt△ABC 周长,设AE 的长为x ,试用含x 的代数式表示△AEF 的面积;⑵是否存在线段EF 将Rt△ABC 的周长和面积同时平分?假设存在,求出此时AE 的长;假设不存在,说明理由. 25.如图,在△ABC 中,DE//BC ,在AB 上取一点F ,使ADE BFCS S ∆∆=.求证:AD 2=AB·BF.26.某生活小区的居民筹集资金1600元,方案在一块上、下底分别为10米,20米的梯形空地上种植花木如图①,⑴他们在△AMD 和△BMC 地带上种植太阳花,单价为8元/㎡,当△AMD 地带种满花后〔图中阴影局部〕共花了160元,请计算种满△BMC 地带所需费用.⑵假设其余地带要种的有玫瑰和茉莉两种花木可供选择,单价分别为12元/㎡和10元/㎡,应选择哪种花木,刚好用完所筹集的资金.⑶假设梯形ABCD 为等腰梯形,面积不变〔如图②〕请你设计一种花坛图案,即在梯形内找到一点P ,使得△APB≌△DPC,且S APD ∆=S BPC ∆,并说明你的理由.A 与CD 边上的点M重合,折线交AD 于E ,交BC 于F ,边AB 折叠后与BC 交于点G ,的中点,求证:DE∶DM∶EM=3∶4∶5.⑵如果M 为CD 上任一点,设AB=2a ,问△CMG 的周长是否与点M 的位置有关?假设有关,请把△CMG 的周长用含DM 的长x 〔即DM=x 〕的代数式表示;假设无关,请说明理由.28.如图,△ABC 中,AB=5,BC=3,AC=4,PQ∥AB,P 点在AC 上〔与A ⑴当△PQC 的面积与四边形PABQ 的面积相等时,求CP 的长. ⑵当△PQC 的周长与四边形PABQ 的周长相等时,求CP 的长.FE DC B A图① BADC 图②B AB⑶试问:在AB 上是否存在一点M ,使得△PQM 为等腰直角三角形,假设不存在,请简要说明理由;假设存在,请求出PQ 的长.29.,如图,在△ABC 中,D 是BC 的中点,且AD=AC ,DE⊥BC 交AB 于点E ,EC 与AD 相交于点F .⑴求证:△ABC∽△FCD;⑵假设S FCD ∆=5,BC=10,求DE 的长.30.如图,,在△ABC 中,BA=BC=20㎝,AC=30㎝,点P 从A 点出发,沿AB 以4㎝/s 的速度向点B 运动;同时点Q 从C 点出发,沿CA 以3㎝/s 的速度向A 点运动,设运动时间为x , ⑴当x 为何值时,PQ∥BC; ⑵当ABC BCQS S ∆∆:=1:3时,求ABC BPQ S S ∆∆:的值;⑶△APQ 能否与△CQB 相似,假设能,求出AP 的长,假设不能,请说明理由.31.如图,△ABC 中,D 为AC 上一点,CD=2DA ,∠BAC=45°,∠BDC=60°,CE⊥BD 于E ,连结AE .⑴写出图中所有相等的线段,并加以说明;⑵图中有无相似三角形,假设有,请写出一对,假设没有,请说明理由; ⑶求△BEC 与△BEA 的面积之比.4.8相似多边形的性质1.2:3;2.2:5,3;3.1:4,1:16;4.1:4;5.75;6.1:16;7.22;8.60;9.C ;10.C ;11.C ;12.D ;13.B ;14.B ;15.C ;16.B ;17.4.8cm ;18.25;19.16;20.⑴提示:延长AD ,BF 交于G .AE:EC=3:2.⑵4. 21.⑴S 1:S=1:4.⑵141+-=x y (0<x <4).22.提示:延长BA ,CD 交于点F .面积=16217.23. ⑴可能,此时BD=72108180-.⑵不可能,当S FCE ∆的面积最大时,两面积之比=925<4.24.⑴S AEF ∆=x x 512522+-.⑵存在.AE=266-.AP Q BCA P QBCMABDECFBPACQBEAC D25.略.26. ⑴640元.⑵选种茉莉花.⑶略.27. ⑴利用勾股定理问题即可解决.⑵答:无关.利用△MCG∽△MDE 的周长比等于相似比可求得△MCG 的面积=4a .28. ⑴CP=22.⑵CP=724.⑶分两种情况①PQ=3760,②PQ=49120. 29.提示:作△ABC 的高AG . ⑴略.⑵DE=38.30. ⑴x =310s .⑵2:9.⑶AP=940或20.31.⑴DE=AD,AE=BE=CE . ⑵有: △ADE∽△ACE 或△BCD∽△ABC. ⑶2:1.。

前言:
该同步训练习题由多位一线国家特级教师针对当前最新的热点、考点、重点、难点、知识点,精心编辑而成。
以高质量的同步训练习题助力考生查漏补缺,在原有基础上更进一步。
(最新精品同步训练习题)
11.3多边形及其内角和
11.3.1 多边形
[学生用书P17]
1.若一个多边形从一个顶点可以引5条对角线,则它是( )
A.五边形 B.六边形
C.七边形 D.八边形
2.下列命题正确的是( )
A.各角都相等的多边形为正多边形
B.各边都相等的多边形为正多边形
C.经过n边形的一个顶点可引(n-2)条对角线
D.正方形是正多边形
3.如图11-3-1,此多边形应记作__ __边形____,AB边的邻边是____和____,顶点E处的内角为____.过顶点A画这个多边形的对角线,共有__ __条,它们把多边形分成__ __个三角形.
图11-3-1
4.如图11-3-2所示,五边形ABCDE是一个__ __五边形,∠E是它的一个__ __,∠FAE是它的一个__ __,AD是它的一条__ __.
图11-3-2
5.分别画出图1133中多边形的全部对角线.
图11-3-3
6.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成6个三角形,则n的值是( )
A.6 B.7 C.8 D.9
7.如图11-3-4所示,O为四边形ABCD内一点,连接OA,OB,OC,OD可以得到几个三角形?所得三角形的个数与四边形ABCD的边数有何关系?
图11-3-4。

八年级数学相似多边形同步练习
2.8 相似多边形同步练习题
第1 题. 如图:
(1)顺次连接矩形各边中点,得到的四边形与原矩形相似吗?
(2)顺次连接正方形各边中点,得到的四边形与原正方形相似吗?
(3)等腰梯形两腰中点的连线将它分成两个梯形相似吗?
答案:解:(1)顺次连接矩形各边中点得到的是菱形.因为对应角不相等,所以它与原矩形不相似.
(2)顺次连接正方形各边中点得到的是正方形.因为各对应角相等,各对应边成比例,所以它与原正方形相似.
(3)因为对应边不成比例,所以等腰梯形两腰中点的连线将它分成的两个梯形不相似.
第2 题. 如图,两块大小不等的等腰直角三角板,它们的对应角相等吗?它们的对应边成比例吗?这两个图形相似吗?
答案:解:由于和都是等腰直三角形,
所以,.设.根据勾股定理,得所以.由于对应角相等、对应边成比例,所以.第3 题. 如图,矩形草坪的长为20m,的长为10m,沿草坪四周外围有1m 宽的环形道路,小路内外边缘所成的矩形与矩形相似吗?
答案:解:根据题意,得.所以,.因为对应边不成比例,
所以矩形与矩形不相似.
第4 题. 已知四边形四边形,,.
(1)求的度数;。

人教版2023-2024学年八年级上册数学《多边形及其内角》同步练习一、单选题1.一个多边形的每个外角都等于与它相邻的内角,这个多边形是( )边形A .四B .五C .六D .八2.若一个多边形的每个内角都是,那么它的边数是( )140︒A .5B .7C .9D .113.中国古代建筑具有悠久的历史传统和光辉的成就,其建筑艺术也是美术鉴赏的重要对象.如图是中国古代建筑中的一个正八边形的窗户,则它的内角和为( )A .B .C .D .1080︒900︒720︒540︒4.如图,一束平行太阳光照射到正五边形上,若∠1=46°,则∠2的度数为( )A .46°B .108°C .26°D .134°5.如图1是一个2×5长方形方格,用图2所示的1×2的黑色长方形(允许只用一种)去填满,共有( )种不同的方法.A .7B .8C .9D .106.如图,四边形中,与相邻的两外角平分线交ABCD 90,ADC ABC ∠=∠=︒ADC ABC ∠∠、于点若则的度数为( ),E 60,A ∠=︒E ∠A .B .C .D .60 50 40 307.如图,要使一个七边形木架不变形,至少要再钉上木条的根数是( )A .1根B .2根C .3根D .4根8.七边形中,、的延长线相交于点.若图中、、、的ABCDEFG AB ED O 1∠2∠3∠4∠外角的角度和为,则的度数为( )220︒BOD ∠A .B .C .D .30︒35︒40︒45︒9.如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )A .B .C .D .240︒220︒180︒330︒10.如图,直线,将一个含角的直角三角尺按图中方式放置,点E 在AB CD ∥60︒EGF 上,边、分别交于点H 、K ,若,则等于( ).AB GF EF CD 64BEF ∠=︒GHC ∠三、解答题21.若一个多边形的内角和等于它的外角和的24.已知一个正n边形的内角和是正三角形内角和的4倍.(1)求n;(2)用边长相等的正n 边形和正三角形两种地板镶嵌地面,则一个公共顶点处需要正n边形和正三角形的个数分别为x、y,求x和y的关系式.25.如图,小明从点A出发,前进10m后向右转30°,再前进10m后又向右转30°,……,如此反复下去,直到她第一次回到出发点A,他所走的路径构成了一个正多边形.(1)求小明一共走了多少米;(2)求这个正多边形的内角和.答案:1.A2.C3.A4.C5.B6.D7.D8.C9.A10.B11.512.③④13.50°或130°14. 15 60°15.18/十八16. 2 817./36度36︒18./度 144︒1443519. 144 10 144020./度180︒18021.这个多边形是十边形22.(1)15;(2)1523.(1)8(2)360︒24.(1)6n =(2)26x y +=25.(1)小明一共走了120米1800 (2)这个多边形的内角和是.。

2023-2024学年人教版数学八年级上册11.3多边形及其内角和同步练习(含答案)2023-2024学年人教版数学八年级上册11.3 多边形及其内角和同步练习一、单选题1.五边形的内角和为()A.720° B.540° C.360° D.180°2.下列角度中,不能成为多边形内角和的是()A.600° B.720° C.900° D.1080°3.一个多边形的内角和是外角和的2倍,这个多边形是()A.四边形B.五边形C.六边形D.八边形4.若从一个正多边形的一个顶点出发,最多可以引5条对角线,则它的一个内角为()A.B.C.D.5.如果一个四边形的面积正好等于它的两条对角线乘积的一半,那么这个四边形一定是()A.菱形B.矩形C.正方形D.对角线互相垂直的四边形6.在一个凸n边形的纸板上切下一个三角形后,剩下一个内角和为1080°的多边形,则n的值为()A.7 B.8C.9 D.以上都有可能7.一个多边形纸片剪去一个内角后,得到一个内角和为2340°的新多边形,则原多边形的边数为()A.14或15或16 B.15或16或17 C.15或16 D.16或178.下列说法中,正确的个数有()①若一个多边形的外角和等于360°,则这个多边形的边数为4;②三角形的高相交于三角形的内部;③三角形的一个外角大于任意一个内角;④一个多边形的边数每增加一条,这个多边形的内角和就增加;⑤对角线共有5条的多边形是五边形.A.1个B.2个C.3个D.4个二、填空题9.若一个正多边形的一个外角等于18°,则这个正多边形的边数是.10.一个多边形的内角和与外角和的比是4:1,则它的边数是.11.如图,点O是正五边形ABCDE的中心,连接BD、OD,则∠BDO =°.12.平面上,将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起,如图,则∠3+∠1﹣∠2=.13.如图所示,∠1+∠2+∠3+∠4+∠5+∠6=度.三、解答题14.一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.15.如图,是四边形的一个外角,且.那么与互补吗?为什么?16.如图,CD∠AF,∠CDE=∠BAF,AB∠BC,∠C=120°,∠E=80°,试求∠F的度数.17.如图,四边形ABCD中,BA丄DA,CD丄BC,BE、DF分别是∠ABC、∠ADC的平分线.(1)∠1与∠2有什么数量关系,为什么?(2)BE与DF有什么位置关系?请说明理由.18.如图,将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后,得到∠1+∠2+∠3+∠4+∠5=460°.(1)求六边形ABCDEF的内角和;(2)求∠BGD的度数.19.如图,五边形中,.(1)求的度数;(2)直接写出五边形的外角和.参考答案1.B 2.A 3.C 4.D 5.D 6.D 7.A 8.B 9.2010.1011.1812.24°13.360 °14.解:根据题意,得(n﹣2)180=1620,解得:n=11.则这个多边形的边数是11,内角和度数是1620度.15.解:与互补,理由如下:∠ ,∠ABC+=180∠∠ABC+∠D=180 ,∠四边形内角和等于360 ,∠ + =360°-(∠ABC+∠D)=180°∠ 与互补.解:如图,连结AD在四边形ABCD中,∠BAD+∠ADC+∠B+∠C=360°.∠AB∠BC,∠∠B=90°.又∠∠C=120°,∠∠BAD+∠ADC=150°.∠CD∠AF,∠∠CDA=∠DAF.又∠∠CDE =∠BAF,∠∠EDA=∠BAD.在四边形ADEF∠DAF+∠EDA+∠F+∠E=360°,∠∠F+∠E=360°(∠ADC+∠BAD)=210°.又∠∠E=80°,∠∠F=130°17.(1)解:∠1+∠2=90°;理由如下:∠BE,DF分别是∠ABC,∠ADC的平分线,∠∠ABC=2∠1,∠ADC=2∠2,∠BA丄DA,CD丄BC,∠∠A=∠C=90°,∠∠ABC+∠ADC=180°,∠2(∠1+∠2)=180°,∠∠1+∠2=90°;(2)解:BE∠DF;理由如下:在∠FCD中,∠∠C=90°,∠∠DFC+∠2=90°,∠∠1+∠2=90°,∠∠1=∠DFC,∠BE∠DF.18.(1)解:六边形ABCDEF的内角和为:180°×(6-2)=720°;(2)解:∠∠1+∠2+∠3+∠4+∠5=460°,∠∠GBC+∠C+∠CDG=720°-460°=260°,∠∠G=360°-(∠GBC+∠C+∠CDG)=100°.19.(1)解:∠AE∠CD,∠∠D+∠E=180°,∠五边形ABCDE中,∠A=100°,∠B=120°,∠.(2)解:根据多边形的外角和定理:五边形的外角和是:°。

4.4 类似多边形一、目标导航1.各角对应相等,各边对应成比例的两个多边形叫做类似多边形;2.类似多边形对应边的比叫做类似比;3.类似多边形的对应边成比例,对应角相等.二、基础过关1.两个矩形必然类似. ( ) 2.两个正方形必然类似. ( ) 3.任意两个菱形都类似. ( ) 4.有一个角相等的两个菱形类似. ( )5.边数不同的多边形必然不类似. ( )三、能力提升6.以下五个命题:①一切的正方形都类似;②一切的矩形都类似;③一切的三角形都类似;④一切的等腰直角三角形都类似;⑤一切的正五边形都类似.其中正确的命题有_______.7.上面图形是类似形的为( )A.一切矩形 B.一切正方形 C.一切菱形 D.一切平行四边形8.以下说法正确的是( )A.一切的三角形都类似 B.一切的正方形都类似C.一切的菱形都类似 D.一切的矩形都类似9.以下四组图形中必类似的是( )A.有一组邻边相等的两个平行四边形 B.有一个角相等的两个等腰梯形C.对角线互相垂直的两个矩形 D.对角线互相垂直且相等的两个四边形.10.以下说法正确的是 ( )A.对应边成比例的多边形都类似 B.四个角对应相等的梯形都类似C.有一个角相等的两个菱形类似 D.有一个锐角相等的两个等腰三角形类似11.四边形ABCD与四边形A1B1C1D1类似,类似比为2:3,四边形A1B1C1D1与四边形A2B2C2D2类似,类似比为5:4,则四边形ABCD与四边形A2B2C2D2类似且类似比为( )A. 5:6 B. 6:5 C. 5:6或6:5 D. 8:1512.若五边形ABCDE∽五边形MNOPQ,且AB=12,MN=6,AE=7,则MQ= .13.一个六边形六边长分别为3,4,5,6,7,8,另一个与它类似的六边形的最短边为6,则其周长为 .14.矩形ABCD 与矩形EFGH 中,AB=4,BC=2,EF=2,FG=1,则矩形ABCD 与矩形EFGH 类似(填“必然”或“不必然”)15.□ABCD 与□ EFGH 中,AB = 4,BC = 2,EF = 2,FG=1,则□ABCD 与□ EFGH 类似(填“必然”或“不必然”)16.把一矩形纸片对折,如果对折后的矩形与原矩形类似,则原矩形纸片的长与宽之比为 .17.如图,图(1)是一个正六边形ABCDEF ,使线段BC 、FE 的长添加相等的数,得图(2),将图(1)中的点A 、D 分别向两边拉长相等的量,得图(3).那么图(1)与图(2)类似吗?图(1)与图(3)类似吗?图(2)与图(3)呢?为甚么?18.如图,等腰梯形ABCD 与等腰梯形A′B′C′D′类似,∠A′=65°,A′B′=6 cm, AB=8 cm , AD=5 cm ,试求梯形ABCD 的各角的度数与A′D′, B′C′的长.19.如图,矩形ABCD 与矩形EDCF 类似,且CD = 1.求:BC·CF 的值.E D A20.如图,在□ABCD 中,AB//EF ,若AB = 1,AD = 2,AE=21AB ,则□ABFE 与□BCDA 类似吗?阐明理由.21.一个矩形剪去一个以宽为边长的正方形后,剩下的矩形与原矩形类似,则原矩形的长与宽之比为多少?四、聚沙成塔如图, □ABCD 中,EF//AD ,设AB=a ,BC=b ,若□AEFD ,□EBCF 都与 □ABCD 类似,试确定a 与b 之间的关系.F E D CB A F E DCB A4.4类似多边形1.×2.√3.×4.√5.√6.①④⑤;7.B ;8.B ;9.C ;10.C ;11.A ;12.27;13.66;14.必然;15.不必然;16.2;17.都不类似,不符合类似定义;18.各角的度数依次为650,650,1150;1150.B 'C '=A 'D '=415cm ;19.BC·CF=1;20.类似;21.2;22.b 2=2a 2.。

3 相似多边形1.若△ABC ∽△A`B`C`,则相似比k 等于( )A .A`B`∶AB B .∠A ∶∠A`C .S △ABC ∶S △A`B`C`D .△ABC 周长∶△A`B`C`周长2.把一个三角形改成和它相似的三角形,如果面积扩大到原来的100倍,那么边长扩大到原来的( )A .10000倍B .10倍C .100倍D .1000倍3.两个相似三角形,其周长之比为3∶2,则其面积比为( )A .2:3B .3∶2C .9∶4D .不能确定4.把一个五边形改成和它相似的五边形,如果面积扩大到原来的49倍,那么对应的对角线扩大到原来的( )A .49倍B .7倍C .50倍D .8倍5.两个相似多边形的一组对应边分别为3 cm 和4.5 cm ,如果它们的面积和为78 cm 2,那么较大多边形的面积为( )A .46.8 cm 2B .42 cm 2C .52 cm 2D .54 cm 26.两个多边形的面积之比为5,周长之比为m ,则m5为( ) A .1 B .55 C .5 D .5 7.在一张1∶10000的地图上,一块多边形地区的面积为6 cm 2,则这块多边形地区的实际面积为( )A .6 m 2B .60000 m 2C .600 m 2D .6000 m 28.已知△ABC ∽△A`B`C`,且BC ∶B`C`=3∶2,△ABC 的周长为24,则△A`B`C`的周长为_______.9.两个相似三角形面积之比为2∶7,较大三角形一边上的高为2,则较小三角形的对应边上的高为_______.10.两个相似多边形最长的的边分为10 cm 和25 cm ,它们的周长之差为60 cm ,则这两个多边形的周长分别为_______.11.四边形ABCD ∽四边形A`B`C`D`,他们的面积之比为36∶25,他们的相似比_____,若四边形A`B`C`D`的周长为15 cm ,则四边形ABCD 的周长为________.12.如图,矩形ABCD 中,E ,F 分别在BC ,AD 上,矩形ABCD ∽矩形ECDF ,且AB =2,S 矩形ABCD =3S 矩形ECDF .试求S 矩形ABCD .13.如图,在△ABC 中,DE ∥BC ,且S △ADE ∶S 四边形BCED ,=1∶2,BC =62,求DE 的长.14.如图,在△ABC 中,∠C =90 o ,D 是AC 上一点,DE ⊥AB 于E ,若AB =10,BC =6,DE =2,求四边形DEBC 的面积.15.△ABC ∽△A`B`C`,21`` B A AB ,边上的中线CD =4 cm ,△ABC 的周长为20 cm ,△A`B`C`的面积是64 cm 2,求∶(1)A`B`边上的中线C`D`的长;(2)△A`B`C`的周长(3)△ABC 的面积参考答案1.D 2.B 3.C 4.B 5.D 6.C 7.B 8.16 9.710.40 cm 和100 cm11.6∶5 18 cm12.设DF =a ,由S 矩形ABCD =3S 矩形ECD F 知AD=3DF=3a , 又AD AB =CDDF ,所以3a 2=4,a =332. 故AD =3a =23,所以S 矩形ABCD =2×23=4313.由S △ADE ∶S 四边形BCED =1∶2知,S △ADE ∶S △ABC =1∶3 又DE ∥BC,故△ADE ∽△ABC , 所以(BC DE )2=31,即(62DE )2=31,所以DE =22 14.由∠A=∠A , ∠AED=∠ACB=90°,故△ADE ∽△ABC . 又AB =10,BC=6, ∠C=90°,由勾股定理可得AC =8,从而S △ABC =21BC×AC=24, 又BC DE =62=31,有ABC S ADE S ∆∆=(31)2=91=24ADE S ∆, 故S △ADE =38.从而S 四边形DEBC =24-38=364 15.(1)C´D´=8 cm ;(2)△A´B´C´的周长为80 cm ;(3)△ABC 的面积为16 cm 2.。

初二数学相似多边形试题1.两个多边形相似的条件是()A.对应角相等B.对应边相等C.对应角相等,对应边相等D.对应角相等,对应边成比例【答案】D【解析】根据多边形相似的条件依次分析各项即可判断.两个多边形相似的条件是对应角相等,对应边成比例,故选D.【考点】多边形相似的条件点评:本题是判定多边形相似的基础应用题,难度一般,学生只需正确理解多边形相似的判定方法即可轻松完成.2.下列图形是相似多边形的是()A.所有的平行四边形;B.所有的矩形C.所有的菱形;D.所有的正方形【答案】D【解析】根据对应角相等,对应边成比例的两个多边形相似,依次分析各项即可判断.所有的平行四边形、矩形、菱形均不一定是相似多边形,而所有的正方形都是相似多边形,故选D.【考点】相似多边形点评:本题是判定多边形相似的基础应用题,难度一般,学生只需熟练掌握特殊四边形的性质即可轻松完成.3.在四边形ABCD与四边形A′B′C′D′中,∠A=∠A′,∠B=∠B′,∠C=∠C′,•∠D=∠D′,且,则四边形________∽四边形________,且它们的相似比是________.【答案】ABCD,A′B′C′D′,2:3【解析】根据对应角相等且对应边成比例的两个多边形相似,相似多边形的相似比等于对应边的比即可得到结果.∵∠A=∠A′,∠B=∠B′,∠C=∠C′,•∠D=∠D′,且,∴四边形ABCD∽四边形A′B′C′D′,且它们的相似比是2:3.【考点】相似多边形的判定和性质点评:本题是相似多边形的判定和性质的基础应用题,难度一般,学生只需正确理解多边形相似的判定方法即可轻松完成.4.把一个矩形剪去一个正方形,若剩余的矩形和原矩形相似,求原矩形的长与宽的比.【答案】(1+):2【解析】根据相似多边形对应边的比等于相似比,设出原来矩形的长和宽,就可得到关于长宽的方程,从而可以解得结果.根据相似多边形对应边的成比例,可得设原矩形ABCD的长AD=x,宽AB=y,则AE=x-y.则解得或(舍去)答:原矩形的长与宽的比为(1+):2.【考点】相似多边形的性质点评:方程思想是初中数学学习中的一个非常重要的思想,很多问题都是转化为方程来解决的;本题重点考查了学生的数形结合的能力,难度不大.5.下列命题正确的是()A.有一个角对应相等的平行四边形相似B.对应边成比例的两个平行四边形相似C.有一个角对应相等的两个等腰梯形相似D.有一个角对应相等的两个菱形相似【答案】D【解析】根据多边形相似的条件即可得到结果.A.有一个角对应相等的平行四边形不一定相似,故本选项错误;B.对应边成比例的两个平行四边形不一定相似,故本选项错误;C.有一个角对应相等的两个等腰梯形不一定相似,故本选项错误;D.有一个角对应相等的两个菱形相似,本选项正确;故选D.【考点】相似多边形点评:特殊四边形的性质的应用是初中数学的重点,是中考常见题,学生需认真掌握并会熟练运用.6.下列说法中正确的是()A.相似形一定是全等形B.不全等的图形不是相似形C.全等形一定是相似形D.不相似的图形可能是全等形【答案】C【解析】根据相似形与全等形的关系依次分析各项即可判断.A.相似形不一定是全等形,B.不全等的图形可能是相似形,D.不相似的图形一定不是全等形,故错误;C.全等形一定是相似形,本选项正确.【考点】相似多边形点评:全等三角形的判定和性质的运用是初中数学平面图形知识里的重点,是中考中的常见知识点,但一般学生往往会把全等和相似看作两个完全不相关的概念,却不了解全等是相似的特例.7.如图所示,有三个矩形,其中是相似形的是()A.甲和乙B.甲和丙C.乙和丙D.甲、乙和丙【答案】B【解析】根据对应角相等且对应边成比例的两个多边形相似即可判断.∵∴是相似形的是甲和丙故选B.【考点】相似多边形点评:特殊平行四边形的性质的应用是初中数学的重点,也是难点,是中考常见题,因而熟练掌握特殊平行四边形的性质极为重要.8.已知如图所示的两个梯形相似,求出未知的x,y,z的长和∠α,∠β的度数.【答案】x=3,y=3,z=6,∠α=70°,∠β=120°【解析】根据两个相似多边形的对应角相等,对应边成比例即可得到结果.∵两个梯形相似∴∠α=180°-110°=70°,∠β=180°-60°=120°,,解得x=3,y=3,z=6.【考点】相似多边形的性质点评:本题是相似多边形的性质的基础应用题,难度一般,学生在解题时只需注意对应字母写在对应位置上,同时具备一定的计算能力,即可轻松解答.9.暑假时,康子帮母亲到鱼店去买鱼,鱼店里有一种“竹笑鱼”,个个都长得非常相似,现在根据大小有两种不同的价格,如图所示,鱼长10cm的每条100日元,鱼长18cm的每条150日元,康子不知道买哪条更好些,你看怎么办?【答案】买18cm长的鱼更合算【解析】因为同一种鱼的密度一样,所以它们的质量比等于体积比,再根据相似体体积的比等于相似比立方,即可判断.设这两种鱼的质量分别为m、M,则而它们的价格比为150:100=1.5,∴买18cm长的鱼更合算.【考点】相似体点评:本题是相似体的基础应用题,难度不大.实际生活中的很多问题往往可以转化为数学问题,学生要具备一定的数学思想及数学方法.10.如图所示,甲、乙是两个不同的正方体,正方体都是相似体,•它们的一切对应线段之比都等于相似比(a:b),设S甲,S乙分别表示两个正方体的表面积,则,又设V甲,V乙分别表示这两个正方体的体积,则,下列几何体中,一定属于相似体的是()A.两个球体B.两个圆柱体C.两个圆锥体D.两个长方体【答案】A【解析】根据阅读材料得到相似体的概念,然后对球体,圆锥体,圆柱体以及长方体进行分析,发现只有球体的形状是完全相同的.A 、两个球体,形状完全相同,是相似体;B、两个圆柱体,如果底面半径或高发生变化,图形就会改变,不是相似体;C、两个圆锥体,如果底面半径或高发生变化,图形就会改变,不是相似体;D、两个长方体,如果长,宽,高中有一个发生变化,图形就会改变,不是相似体;故选A.【考点】相似图形点评:阅读理解题主要考查学生阅读分析问题的能力,在中考中很常见,这类问题往往难度不大,但需要同学们仔细认真,注意把握题目中的关键语句.。

相似多边形一、选择题1.用放大镜将图形放大,应该属于()A.平移变换B.相似变换C.对称变换D.旋转变换2.小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中的对应线段是()A.FG B.FH C.EH D.EF3.在1:5000的地图上,A、B两地的图上距离为3cm,则A、B两地间实际距离为()A.15m B.150m C.1500m D.15000m4.如图所示的两个四边形相似,则∠的度数是()a1380750600600A.870B.600C.750D.12005.下列结论不正确的是()A.所有的等腰直角三角形都相似B.所有的正方形都相似C.所有的矩形都相似D.所有的正八边形都相似二、填空题6.两地相距350千米,在1﹕10000000的地图上相距厘米.7.下列情形:①用眼睛看月亮和用望远镜看月亮,看到的图象是相似的图形;②用彩笔在黑板上写上三个大字1、2、3,它们是相似图形;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,这两个字是相似图形;以上说法你认为正确的是,错误的是.(填序号)8.△ABC中,BC=54cm,CA=45cm,AB=63cm,另一个与它相似的三角形的最短边为15cm,则周长为__________.9.已知两个圆形的相似比是3∶4,其中一个圆形的半径长为4cm,那么另一个圆形的半径长为.10.下面各组中的两个图形,是形状相同的图形,是形状不同的图形.(填序号)三、解答题11.视力表对我们来说并不陌生.如图是视力表的一部分,其中开口向上的两个“E”之间的图形变换是属于什么变换?12.如图,赵师傅透过平举的放大镜从正上方看到水平桌面上的菱形图案的一角,请判断∠A与放大镜中的∠C的大小关系?13.在比例尺是1:8000的南京市城区地图上,太平南路的长度约为25cm,它的实际长度约为多少米?14.如图所示,四边形ABCD 和四边形A 1B 1C 1D 1相似,已知∠A =120°,∠B =85°,∠C 1=75°,AB =10,A 1B 1=16,CD =18,那么四边形ABCD 和四边形A 1B 1C 1D 1相似比是多少?∠D 1的度数是多少?C 1D 1的长度是多少?11B15.如果整张报纸与半张报纸相似,则此报纸的长与宽的比是多少?参考答案1.B.【解析】根据轴对称变换、平移变换、旋转变换、相似变换的特点,结合图形即可得出答案.解:由一个图形到另一个图形,在改变的过程中形状不变,大小产生变化,属于相似变换.故选B.2.D【解析】由图可知,点A、E是对应顶点,点B、F是对应顶点,点D、H是对应顶点,所以,甲图中的线段AB在乙图中的对应线段是EF,故选D.3.B.【解析】设两地的实际距离为cm,根据题意得:135000x=,解得:15000x=,∵15000cm=150m,∴两地的实际距离150m.故选B.4.A【解析】根据相似多边形的对应角相等以及四边形的内角和可知∠=3600-600-1380-750=870.故选:A.5.C【解析】A.所有的等腰直角三角形两腰相等,所以都相似,A是正确的.所有的正多边形(边数一样的)也是相似的,所以B、D正确.而所有的矩形却是不一定相似的,故C错误.故选C.6.【解析】比例尺1﹕10000000的意思是图上1厘米表示实际距离10000000厘米,即100千米,所以实际的350千米在图上是350÷100=(cm).故答案为7.①,②③【解析】根据相似图形的定义,对题目中的条件进行一一分析,确定正确和错误答案.解:①用眼睛看月亮和用望远镜看月亮,形状相同,但大小不一定相同,看到的图象是相似的图形,故正确;②用彩笔在黑板上写上三个大字1,2,3,它们形状不同,故错误;③用粉笔在黑板上写上“天”和用毛笔在纸上写上“天”,属于不唯一确定图形,故错误.∴答案为正确的是①,错误的是②③.8.54cm【解析】△ABC中,最短的边为45cm,另一个与之相似的三角形最短边为15cm,所以两个三角形边长之比为1:3,另一个三角形的另外两边长分别为:54×13=18(cm),63×13=21(cm),所以另一个三角形的周长为15+18+21=54(cm).故答案为54cm.9.3cm或163cm【解析】由于不明确半径长为4cm的圆形,故应分两种情况讨论.解:设另一个圆的半径是x cm.半径长的比就是相似比,有两种情况:当x:4=3:4时,解得x=3;当4:x=3:4时,解得x=163.故另一个圆的半径为3cm或163cm.10.(3)、(5);(1)、(2)、(4)、(6)【解析】通过观察只有(3)(5)的形状相同,其它几组图形都有区别.解:(1)中左边图形是圆,右边图形是椭圆,形状不同.(2)中左边是正六边形,右边不是正六边形,形状不同.(3)中两个图形形状相同.(4)中左边是长方形,右边正方形,形状不同.(5)中两个图形形状相同.(6)中左边是圆形脸,右边是椭圆形脸,形状不同.因此,(3)(5)组中图形形状相同,(1)(2)(4)(6)组中图形形状不同.故答案为(3)(5);(1)(2)(4)(6)11.相似变换【解析】平移旋转轴对称等变换都不改变图形的形状与大小.而两个字母的大小发生了变化所以属于相似相似变换.12.∠A与放大镜中的∠C相等.【解析】原来的图形和放大的图形是相似的,根据相似图形的对应角相等及菱形的性质可以判定∠A与放大镜中的∠C相等.解:由于图形放大或缩小后,形状没有发生变化,结合相似的性质,可判定放大前后的∠C是相等的,又根据菱形的性质可知∠A=∠C.所以∠A与放大镜中的∠C相等.13.2000m【解析】根据比例尺=图上距离:实际距离,列比例式,根据比例的基本性质即可求得结果.解:设它的实际长度为x cm,则=x =200000200000cm=2000m .答:太平南路的实际长度约为2000米. 14.58,80°,1445【解析】解:∵四边形ABCD 和四边形A 1B 1C 1D 1相似, ∴相似比为1111851610C D DCB A AB === ∴B B A A ∠=∠∠=∠11,︒=∠-∠-∠-︒=∠803601111C B A D∵111851610C D DC B AB ====85 514411=∴C D 15.报纸的长与宽的比是:1【解析】根据相似形对应边的比相等,列式即可得出长与宽的比. 解:设报纸的长为2x ,报纸的宽为y , ∵整张报纸与半张报纸相似, 则;即=2;2x :y =:1.答:报纸的长与宽的比是:1。

相似多边形的性质练习题(含答案)题目一已知多边形ABCD与多边形EFGH是相似多边形,且已知各个角度的度数如下:∠A = 60°,∠B = 80°,∠C = 100°,∠D = 120°。
如果∠E = 40°,求∠F,∠G和∠H的度数。
解答由于多边形ABCD与多边形EFGH是相似多边形,对应角度相等,因此∠A = ∠E,∠B = ∠F,∠C = ∠G,∠D = ∠H。
已知∠A = 60°,∠E = 40°,代入可得:∠B = ∠F = 60°∠C = ∠G = 80°∠D = ∠H = 100°所以∠F的度数为60°,∠G的度数为80°,∠H的度数为100°。
题目二已知多边形PQRS与多边形UVWX是相似多边形,且已知各边的长度比如下:PQ:UV = 3:4,QR:VW = 2:3,RS:WX = 5:7。
如果PQ = 6 cm,求UV,VW和WX的长度。
解答由于多边形PQRS与多边形UVWX是相似多边形,对应边长的比相等,根据已知条件可得:PQ:UV = 3:4QR:VW = 2:3RS:WX = 5:7已知PQ = 6 cm,代入可得:UV = (PQ * 4) / 3 = (6 * 4) / 3 = 8 cmVW = (QR * 3) / 2 = (QR * 3) / 2 = 9 cmWX = (RS * 7) / 5 = (RS * 7) / 5 = 2.8 cm所以UV的长度为8 cm,VW的长度为9 cm,WX的长度为2.8 cm。

人教版八年级数学上册《多边形》同步训练习题11.3.1《多边形》同步训练习题一.选择题(共7小题)1.(2015秋•克什克腾旗校级月考)下列图中不是凸多边形的是()A.B.C.D.2.(2015秋•克什克腾旗校级月考)下列图形中,是正多边形的是()A.直角三角形 B.等腰三角形 C.长方形D.正方形3.n边形的内角的和等于()A.(n﹣1)×180°B.(n﹣2)×180°C.(n﹣3)×180°D.(n﹣4)×180°4.(2015秋•三亚校级月考)一个四边形截去一个内角后变为()A.三角形B.四边形C.五边形D.以上均有可能5.(2014秋•朝阳区期末)在六边形内任取一点,把这个点与六边形的各顶点分别连接可以得到()A.4个三角形B.5个三角形C.6个三角形D.7个三角形6.(2012秋•渝中区校级期末)从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成()个三角形.A.6 B.5 C.8 D.77.从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到200 3个三角形,则这个多边形的边数为()A.2001 B.2005 C.2004 D.2006二.填空题(共7小题)8.(2014春•邵阳期末)能伸缩的校门,它利用了四边形的一个性质是.9.(2013秋•景泰县校级月考)在平面内,,的多边形叫正多边形.10.多边形相邻两边组成的角叫做它的;多边形的边与它的邻边的延长线组成的角叫做多边形的;连接多边形不相邻的两个顶点的线段叫做多边形的.11.若一个多边形截去一个角后,变成六边形,则原来多边形的边数可能是.12.若一个六边形的各条边都相等,当边长为3cm时,它的周长为cm.13.如图所示,将多边形分割成三角形﹨图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出个三角形.14.(2011•肇庆)如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是.三.解答题(共4小题)15.用两个一样大小的含30°角的三角板可以拼成多少个形状不同的四边形?请画图说明.16.(2012春•西城区校级期中)把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.求:(1)原来的多边形是几边形?(2)把原来的多边形分割成了多少个多边形?17.已知线段AC=8,BD=6.(1)已知线段AC垂直于线段BD.设图1,图2和图3中的四边形ABCD的面积分别为S1﹨S2和S3,则S1= ,S2= ,S3= ;(2)如图4,对于线段AC与线段BD垂直相交(垂足O不与点A,C,B ,D重合)的任意情形,请你就四边形ABCD面积的大小提出猜想,并证明你的猜想;(3)当线段BD与AC(或CA)的延长线垂直相交时,猜想顺次连接点A,B,C,D,A所围成的封闭图形的面积是多少?18.已知正n边形的周长为60,边长为a(1)当n=3时,请直接写出a的值;(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.人教版八年级数学上册11.3.1《多边形》同步训练习题参考答案一.选择题(共7小题)1.(2015秋•克什克腾旗校级月考)下列图中不是凸多边形的是()A.B.C.D.选A2.(2015秋•克什克腾旗校级月考)下列图形中,是正多边形的是()A.直角三角形 B.等腰三角形 C.长方形D.正方形【考点】多边形.【分析】根据正多边形的定义;各个角都相等,各条边都相等的多边形叫做正多边形可得答案.【解答】解:正方形四个角相等,四条边都相等,故选:D.【点评】此题主要考查了正多边形,关键是掌握正多边形的定义.3.n边形的内角的和等于()A.(n﹣1)×180°B.(n﹣2)×180°C.(n﹣3)×180°D.(n﹣4)×180°【考点】多边形;多边形内角与外角.【分析】从四边形的一个顶点出发可以画1条对角线,把四边形分成两个三角形,所以四边形内角和为:(4﹣2)×180°,从五边形的一个顶点出发可以画2条对角线,把五边形分成三个三角形,所以四边形内角和为:(5﹣2)×180°,从n边形的一个顶点出发可以画(n﹣3)条对角线,把四边形分成(n﹣2)个三角形,所以n边形内角和为:(n﹣2)×180°.【解答】解:因为三角形的内角和是180°,四边形的内角和是360°,五边形的内角和是540°,∴n边形的内角的和公式:(n﹣2)×180°,故选:B.【点评】此题主要考查了多边形内角和公式.正确的记忆多边形内角和公式是解决问题的关键.4.(2015秋•三亚校级月考)一个四边形截去一个内角后变为()A.三角形B.四边形C.五边形D.以上均有可能【考点】多边形.【分析】一个四边形截去一个角是指可以截去两条边,而新增一条边,得到三角形;也可以截去一条边,而新增一条边,得到四边形;也可以直接新增一条边,变为五边形.可动手画一画,具体操作一下.【解答】解:如图可知,一个四边形截去一个角后变成三角形或四边形或五边形.故选:D.【点评】本题考查了多边形,解决此类问题的关键是动手画一画准确性高,注意不要漏掉情况.5.(2014秋•朝阳区期末)在六边形内任取一点,把这个点与六边形的各顶点分别连接可以得到()A.4个三角形B.5个三角形C.6个三角形D.7个三角形【考点】多边形.【分析】根据六边形有六个顶点,连接六个顶点,可得六个三角形.【解答】解:在六边形内任取一点,把这个点与六边形的各顶点分别连接可以得到六个三角形,故选:C.【点评】本题考查了多边形,利用了图形的分割:六个顶点可分割成六个三角形.6.(2012秋•渝中区校级期末)从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成()个三角形.A.6 B.5 C.8 D.7【考点】多边形.【专题】规律型.【分析】从n边形的一个顶点出发,连接这个点与其余各顶点,可以把一个四边形分割成(n﹣2)个三角形.【解答】解:从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成7﹣2=5个三角形.故选:B.【点评】本题考查的知识点为:从n边形的一个顶点出发,可把n边形分成(n﹣2)个三角形.7.(2010秋•毕节市校级期中)从多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,则这个多边形的边数为()A.2001 B.2005 C.2004 D.2006【考点】多边形.【分析】可根据多边形的一点(不是顶点)出发,连接各个顶点得到的三角形个数与多边形的边数的关系求解.【解答】解:多边形一条边上的一点(不是顶点)出发,连接各个顶点得到2003个三角形,则这个多边形的边数为2003+1=2004.故选C.【点评】多边形一条边上的一点(不是顶点)出发,连接各个顶点得到的三角形个数=多边形的边数﹣1.二.填空题(共7小题)8.(2014春•邵阳期末)能伸缩的校门,它利用了四边形的一个性质是四边形的不稳定性.【考点】多边形.【分析】由四边形的特性可知,四边形具有不稳定性,所以容易变形,伸缩门的运用了四边形易变形的特性.【解答】解:伸缩门做成四边形的形状,是利用四边形的易变形的特性.故答案为:四边形的不稳定性.【点评】此题主要考查了四边形的特性是容易变形.9.(2013秋•景泰县校级月考)在平面内,各边都相等,各内角也相等的多边形叫正多边形.【考点】多边形.【分析】利用正多边形的定义直接填空得出即可.【解答】解:如果多边形的各边都相等,各内角也相等,那么就称它为正多边形.故答案为:各边都相等,各内角也相等.【点评】此题主要考查了掌握正多边形概念.如果多边形的各边都相等,各内角也相等,那么就称它为正多边形.10.多边形相邻两边组成的角叫做它的内角;多边形的边与它的邻边的延长线组成的角叫做多边形的外角;连接多边形不相邻的两个顶点的线段叫做多边形的对角线.【考点】多边形.【分析】根据多边形的定义以及外角的定义和对角线的定义分别分析得出即可.【解答】解:多边形相邻两边组成的角叫做它的内角;多边形的边与它的邻边的延长线组成的角叫做多边形的外角;连接多边形不相邻的两个顶点的线段叫做多边形的对角线.故答案为:内角,外角,对角线.【点评】此题主要考查了多边形有关定义,熟练掌握相关概念是解题关键.11.(2011春•郯城县期中)若一个多边形截去一个角后,变成六边形,则原来多边形的边数可能是5,6,7 .【考点】多边形.【分析】实际画图,动手操作一下,可知六边形可以是五边形﹨六边形﹨七边形截去一个角后得到.【解答】解:如图可知,原来多边形的边数可能是5,6,7.【点评】此类问题要从多方面考虑,注意不能漏掉其中的任何一种情况.12.若一个六边形的各条边都相等,当边长为3cm时,它的周长为18cm.【考点】多边形.【专题】计算题.【分析】由于六边形的各条边都相等,则六边形的周长=各条边的长×6.【解答】解:六边形的周长为:3×6=18cm.故这个六边形的周长为18cm.故答案为:18.【点评】本题考查了多边形的周长计算,是基础题型,比较简单.13.(2008秋•高碑店市期中)如图所示,将多边形分割成三角形﹨图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出,n边形可以分割出(n﹣1)个三角形.【考点】多边形.【分析】(1)三角形分割成了两个三角形;(2)四边形分割成了三个三角形;(3)以此类推,n边形分割成了(n﹣1)个三角形.【解答】解:n边形可以分割出(n﹣1)个三角形.【点评】此题注意观察:是连接n边形的其中一边上的点.根据具体数值进行分析找规律.n边形分割成了(n﹣1)个三角形.14.(2011•肇庆)如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是n2+2n .【考点】多边形.【专题】压轴题;规律型.【分析】第1个图形是2×3﹣3,第2个图形是3×4﹣4,第3个图形是4×5﹣5,按照这样的规律摆下去,则第n个图形需要黑色棋子的个数是(n+1)(n+2)﹣(n+2)=n2+2n.【解答】解:第n个图形需要黑色棋子的个数是n2+2n.故答案为:n2+2n.【点评】首先计算几个特殊图形,发现:数出每边上的个数,乘以边数,但各个顶点的重复了一次,应再减去.三.解答题(共4小题)15.用两个一样大小的含30°角的三角板可以拼成多少个形状不同的四边形?请画图说明.【考点】多边形.【专题】作图题.【分析】若让它们的斜边重合,则可以拼出矩形或一组对角是直角的四边形;若让它们的直角边重合,则可以拼出两种不同的平行四边形.【解答】解:四个.如图所示:【点评】能够让它们的边分别重合进行不同的拼图.考查了学生的实践能力.16.(2012春•西城区校级期中)把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.求:(1)原来的多边形是几边形?(2)把原来的多边形分割成了多少个多边形?【考点】多边形;规律型:图形的变化类.【分析】把多边形沿直线剪开,每增加一个多边形,边数的增加会出现以下三种情况:①当直线经过两个顶点时,增加两条边;②当直线经过一个顶点时,增加三条边;③当直线不经过顶点时,增加四条边.于是,当将原多边形分割成4个小多边形,最多可以增加4×3=12条边,当将原多边形分割成8个小多边形,最少可以增加2×7=14条边.所以分割后的多边形的个数是5,6,7中的一个.设原多边形的边数是n,分割成边数为a1,a2,…,a m的m个多边形,则m 个多边形的总边数为a1+a2+…+a m由题意,可得方程a1+a2+…+a m=n+13,180(a1﹣2)+180(a2﹣2)+…+180(a m﹣2)=1.3×180(n﹣2),再整理可得3n+20m=156,再讨论出二元一次方程的整数解即可.【解答】解:设原多边形的边数是n,分割成边数为a1,a2,…,a m的m 个多边形,则m个多边形的总边数为a1+a2+…+a m,由题意有a1+a2+…+a m=n+13,180(a1﹣2)+180(a2﹣2)+…+180(a m﹣2)=1.3×180(n﹣2),则3n+20m=156,解得:m=6,n=12.故原来的多边形是12边形,把原来的多边形分割成了6个小多边形.【点评】此题主要考查了多边形,关键是掌握多边形内角和公式180°(n﹣2).17.已知线段AC=8,BD=6.(1)已知线段AC垂直于线段BD.设图1,图2和图3中的四边形ABCD的面积分别为S1﹨S2和S3,则S1= 24 ,S2= 24 ,S3= 24 ;(2)如图4,对于线段AC与线段BD垂直相交(垂足O不与点A,C,B ,D重合)的任意情形,请你就四边形ABCD面积的大小提出猜想,并证明你的猜想;(3)当线段BD与AC(或CA)的延长线垂直相交时,猜想顺次连接点A,B,C,D,A所围成的封闭图形的面积是多少?【考点】多边形;三角形的面积.【专题】探究型.【分析】(1)根据三角形的面积公式进行计算;(2)根据(1)中的计算结果,发现三个图形的面积都是24.根据三角形的面积公式进行证明;(3)仍然把四边形的面积分割成两个三角形,按三角形的面积公式进行证明.【解答】解:(1)S1=24,S2=24,S3=24;(2)对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,四边形ABCD的面积为定值24.证明如下:∵AC⊥BD,∴S△BAC=AC•OB,S△DAC=AC•OD,∴S四边形ABCD=AC•OB+AC•OD=AC•(OB+OD)=AC•BD=24.(3)顺次连接点A,B,C,D,A所围成的封闭图形的面积仍为24.证明:∵AC⊥BD,∴S△ABD=AO•BD,S△BCD=CO•BD,∴S四边形ABCD=S△ABD+S△BCD=AO•BD+CO•BD=BD(AO+CO)=BD•AC=24.【点评】此题注意发现:对角线互相垂直的四边形的面积总等于对角线乘积的一半.18.已知正n边形的周长为60,边长为a(1)当n=3时,请直接写出a的值;(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.【点评】读懂题意,找到相应量的等量关系是解决问题的关键.。

八年级下册数学相似多边形与相似三角形基础题北师版一、单选题(共10道,每道10分)1.下列说法正确的是()A.所有角对应相等的两个四边形相似B.所有边对应成比例的两个四边形相似C.相似图形是形状相同的图形。
D.相似图形是形状相同、大小相等的图形答案:C试题难度:三颗星知识点:相似多边形的定义2.已知一个多边形的最长边为15,最短边为5,另一个和它相似的多边形的最长边为12,则这个多边形的最短边为()A.6B.5C.4D.3答案:C试题难度:三颗星知识点:相似比3.如图,已知△ABC∽△ADE,AB=30cm,AD=18cm,BC=20cm,,则DE长为()cm.A.12B.10C.8D.6答案:A试题难度:三颗星知识点:相似求边长、角度4.如图:△ABC∽△EFG,且AB:EF=1:2,D、H分别是边BC、FG中点,则AD:EH等于()A.1:2B.1:3C.1:4D.1:8答案:A试题难度:三颗星知识点:相似比与高线比、中线比、对应角平分线比5.已知两个相似三角形的对应中线比为1:3,较大的三角形的周长为18cm,则较小的三角形的周长为()A.6cmB.9mC.63cmD.54cm答案:A试题难度:三颗星知识点:相似比与周长、面积6.在△ABC与△DEF中,∠A=∠D=70°,∠B=60°,则当∠F=()度时,△ABC∽△DEF。
A.80°B.70°C.60°D.50°答案:D试题难度:三颗星知识点:两角对应相等7.在△ABC与△DEF中,AB=8,BC=6,AC=4,DE=4,EF=3,则当DF=()时,△ABC∽△DEF。
A.2B.3C.4D.6答案:A试题难度:三颗星知识点:三边对应成比例8.如图:已知△ABC,AB=AC=6,∠B=75°,则下列4个三角形中,与△ABC相似的是()A.B.C.D.答案:C试题难度:三颗星知识点:两边对应成比例且夹角相等9.下列说法错误的是()A.有一组对应角都为30°的两个直角三角形相似B.顶角都为36°的两等腰三角形相似C.所有的等腰三角形相似D.所有的等腰直角三角形相似答案:C试题难度:三颗星知识点:特殊图形的相似判定10.如图,已知∠1=∠2,添加下列一个条件后,无法判定△ABC∽△ADE的是()A.B.C.∠B=∠DD.∠C=∠AED答案:B试题难度:三颗星知识点:相似的判定综合。
11.3.1 多边形【基础练习】知识点 1 多边形及其相关概念1.如图1,不是凸多边形的是 ()图12.如图2所示的四边形的表示方法正确的是 ()图2A.四边形ABCDB.四边形ACBDC.四边形ABDCD.四边形ADBC知识点 2 多边形的对角线3.图3中的图形是边形,它有个内角,条边,从一个顶点出发的对角线有条,把该多边形分成个三角形.图34.从十边形的一个顶点出发可以画出的对角线的条数是 ()A.7B.8C.9D.105.从n边形的一个顶点出发,分别连接这个顶点和与其不相邻的各个顶点,若把这个多边形分割成7个三角形,则n的值是 () A.6 B.7 C.8 D.9知识点 3 正多边形6.下列图形中属于正多边形的有 ()①等边三角形;②长方形;③正方形;④梯形;⑤圆.A.1个B.2个C.3个D.4个7.下列说法正确的是 ()A.五个角都相等的五边形是正五边形B.六条边都相等的六边形是正六边形C.四个角都是直角的四边形是正方形D.七个角都相等的七边形不一定是正七边形【能力提升】8.把一张形状是多边形的纸片剪去其中某一个角,剩下的部分是一个四边形,则这张纸片原来的形状不可能是()A.六边形B.五边形C.四边形D.三角形9.下列说法正确的是 ()A.由一些线段首尾顺次相接组成的图形叫做多边形B.多边形的两边所在直线组成的角是这个多边形的内角或外角C.各个角都相等,各条边都相等的多边形是正多边形D.连接多边形的两个顶点的线段,叫做多边形的对角线10.若一个多边形的对角线的条数恰好为边数的2倍,则这个多边形的边数为 ()A.6B.7C.8D.911.如图4,四边形ABCD去掉∠C后,剩下的新图形是几边形?请画出图形.图412.(1)如图5①,O为四边形ABCD内一点,连接OA,OB,OC,OD,可以得到几个三角形?它与边数有何关系?(2)如图②,点O在五边形ABCDE的边AB上,连接OC,OD,OE,可以得到几个三角形?它与边数有何关系?(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?图511.3.1 多边形1.C [解析] 只要有一个内角大于180°,就能确定该图形不是凸多边形.2.A3.五 5 5 2 34.A [解析] 从n 边形的一个顶点出发可以作(n-3)条对角线.5.D6.B [解析] 各个角都相等,各条边都相等的多边形是正多边形,只有①③属于正多边形.7.D [解析] 正多边形必须满足各条边都相等,各个角都相等,这两个条件缺一不可.8.A9.C10 B [解析] 六边形对角线的条数为6×(6-3)×12=9,七边形对角线的条数为7×(7-3)×12=14,八边形对角线的条数为8×(8-3)×12=20,九边形对角线的条数为9×(9-3)×12=27.故选B .11.解:有三种情况,它们分别是三角形、四边形、五边形,作图如下:12.解:(1)4个,它与边数相等. (2)4个,它等于边数减1. (3)4个,它等于边数减2.。
八年级数学 相似多边形 同步练习
1. 两个相似多边形一组对应边分别为3cm ,4.5cm ,那么它们的相似比为( )
A .32
B .23
C .94
D . 4
9 2. 在矩形ABCD 中,E ,F 分别为AB ,CD 的中点,如果矩形ABCD ∽矩形EFCB ,那么它们的相似比为( )
A .2
B .2
2 C .2 D .21 3. 一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为( )
A .6
B .8
C .12
D .10
4. 如果多边形ABCDEF ∽多边形A`B`C`D`E`F`,且∠A =68o ,则∠A`等于( )
A .22 o
B .112 o
C .68 o
D .54o
5. 相似多边形对应边之比叫做______.
6. 两个相似多边形的最长边分别为10cm 和20cm ,其中一个多边形的最短边为5cm ,则另一个多边形的最短边为______.
7. 在梯形ABCD 中,AB ∥CD ,AB =60,CD =15,E ,F 分别为AD ,BC 上一点,且EF ∥AB ,若梯形DEFC ∽梯形EABF ,那么EF =______.
8. E,F 分别为矩形ABCD 的边AD ,BC 的中点,若矩形ABCD ∽矩形EABF ,AB =1,求矩形ABCD 的面积。
9. 梯形ABCD 中,AD ∥BC ,E ,F 分别为AB ,CD 上一点,且梯形AEFD ∽梯形EBCF ,若AD =4,BC =9。
试求AE :EB 的值。
10.
对应角相等的两个多边形一定是相似多边形吗?两个多边形的对应边的比值都相等,这样的两个多边形也是相似多边形吗?试分别举例说明。
11.
在长为10,宽为8的矩形ABCD 中,点E 在长AD 上,F 在AB 上,若所得到的矩形EFCD ∽矩形ABCD ,试问AE 之长是多少?请说明理由。
答案:1.A 2.A 3.B 4.C 5.相似比 6.10cm 或2.5cm 7.30
8.由AB AE AD AB =,故,2,2
2==AD AE 故S 矩形ABCD =2 9.由
BC EF EF AD =,故EF =6,所以3264===EF AD EB AE 。
10.对应角相等的两个多边形未必相似,如矩形和正方形;两个多边形的对应边成比例,这两个多边形未必相似,如;菱形和正方形。
11.AE =3.6。
理由:由
AD AB DC DE =,得DE =6.4,则AE =10-6.4=3.6。