浙教版2021年中考数学总复习《圆》(含答案)

浙教版2021年中考数学总复习《圆》一、选择题1.如图，在⊙O中与∠1一定相等的角是( )A．∠2 B．∠3 C．∠4 D．∠52.如图，⊙O是△ABC的外接圆，∠OCB=40°，则∠A的度数为（）A.60°B.50°C.40°D.30°3.如图，⊙O中，ABDC是圆内接四边形，∠BOC=110°，则∠BDC的度数是（）A.110°B.70°C.55°D.125°4.如图，四边形ABCD内接于半圆O，已知∠ADC=140°，则∠AOC的大小是（）A.40°B.60°C.70°D.80°5.如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC．若∠P=40°，则∠ABC的度数为（）A．20° B．25° C．40° D．50°6.阅读理解：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（）A．（60°，4）B．（45°，4）C．（60°，2）D．（50°，2）7.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c值为（）A.1：2：3B.3：2：1C.1：：D.：：18.如图，四边形ABCD内接于⊙O，F是上一点，且=，连接CF并延长交AD的延长线于点E，连接AC，若∠ABC=105°，∠BAC=25°，则∠E的度数为（）A．45° B．50° C．55° D．60°二、填空题9.将面积为32π的半圆围成一个圆锥的侧面，则这个圆锥的底面半径为．10.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图，CD为的直径，弦AB⊥CD于E，CE=1寸，AB=10寸，求直径CD的长”。

2021年浙江中考数学真题汇编——专题7圆一．选择题〔共7小题〕1．〔2021•衢州〕扇形的半径为6，圆心角为150°，那么它的面积是〔 〕 A ．32πB ．3πC ．5πD ．15π2．〔2021•金华〕如图，在Rt △ABC 中，∠ACB ＝90°，以该三角形的三条边为边向形外作正方形，正方形的顶点E ，F ，G ，H ，M ，N 都在同一个圆上．记该圆面积为S 1，△ABC 面积为S 2，那么S 1S 2的值是〔 〕A ．5π2B ．3πC ．5πD ．11π23．〔2021•绍兴〕如图，正方形ABCD 内接于⊙O ，点P 在AB ̂上，那么∠BPC 的度数为〔 〕A ．30°B ．45°C ．60°D ．90°4．〔2021•嘉兴〕平面内有⊙O 和点A ，B ，假设⊙O 半径为2cm ，线段OA ＝3cm ，OB ＝2cm ，那么直线AB 与⊙O 的位置关系为〔 〕 A ．相离B ．相交C ．相切D ．相交或相切5．〔2021•丽水〕如图，AB 是⊙O 的直径，弦CD ⊥OA 于点E ，连结OC ，OD ．假设⊙O 的半径为m ，∠AOD ＝∠α，那么以下结论一定成立的是〔 〕A．OE＝m•tanαB．CD＝2m•sinαC．AE＝m•cosαD．S△COD=12m2•sinα6．〔2021•湖州〕如图，在矩形ABCD中，AB＝1，BC=√3，点P是AD边上的一个动点，连结BP，点C关于直线BP的对称点为C1，当点P运动时，点C1也随之运动．假设点P从点A运动到点D，那么线段CC1扫过的区域的面积是〔〕A．πB．π+3√34C．3√32D．2π7．〔2021•湖州〕如图，点O是△ABC的外心，∠A＝40°，连结BO，CO，那么∠BOC的度数是〔〕A．60°B．70°C．80°D．90°二．填空题〔共5小题〕8．〔2021•杭州〕如图，⊙O的半径为1，点P是⊙O外一点，且OP＝2．假设PT是⊙O的切线，T为切点，连结OT，那么PT＝．9．〔2021•宁波〕抖空竹在我国有着悠久的历史，是国家级的非物质文化遗产之一．如图，AC，BD分别与⊙O相切于点C，D，延长AC，BD交于点P．假设∠P＝120°，⊙O的̂的长为cm．〔结果保存π〕半径为6cm，那么图中CD10．〔2021•台州〕如图，将线段AB绕点A顺时针旋转30°，得到线段AC．假设AB＝12，̂长度为．〔结果保存π〕那么点B经过的路径BC11．〔2021•温州〕假设扇形的圆心角为30°，半径为17，那么扇形的弧长为．12．〔2021•温州〕如图，⊙O与△OAB的边AB相切，切点为B．将△OAB绕点B按顺时针方向旋转得到△O′A′B，使点O′落在⊙O上，边A′B交线段AO于点C．假设∠A′＝25°，那么∠OCB＝度．三．解答题〔共8小题〕13．〔2021•衢州〕如图，在△ABC中，CA＝CB，BC与⊙A相切于点D，过点A作AC的垂线交CB的延长线于点E，交⊙A于点F，连结BF．〔1〕求证：BF是⊙A的切线．〔2〕假设BE＝5，AC＝20，求EF的长．14．〔2021•衢州〕如图1，点C是半圆O的直径AB上一动点〔不包括端点〕，AB＝6cm，过点C作CD⊥AB交半圆于点D，连结AD，过点C作CE∥AD交半圆于点E，连结EB．牛牛想探究在点C运动过程中EC与EB的大小关系．他根据学习函数的经验，记AC＝xcm，EC＝y1cm，EB＝y2cm．请你一起参与探究函数y1、y2随自变量x变化的规律．通过几何画板取点、画图、测量，得出如下几组对应值，并在图2中描出了以各对对应值为坐标的点，画出了不完整图象．x……y1……y2……〔1〕当x＝3时，y1＝．〔2〕在图2中画出函数y2的图象，并结合图象判断函数值y1与y2的大小关系．〔3〕由〔2〕知“AC取某值时，有EC＝EB〞．如图3，牛牛连结了OE，尝试通过计算EC，EB的长来验证这一结论，请你完成计算过程．̂上存在点E，满足AÊ=CD̂，15．〔2021•宁波〕如图1，四边形ABCD内接于⊙O，BD为直径，AD连结BE并延长交CD的延长线于点F，BE与AD交于点G．〔1〕假设∠DBC＝α，请用含α的代数式表示∠AGB．〔2〕如图2，连结CE，CE＝BG．求证：EF＝DG．〔3〕如图3，在〔2〕的条件下，连结CG，AD＝2．①假设tan∠ADB=√32，求△FGD的周长．②求CG的最小值．16．〔2021•台州〕如图，BD是半径为3的⊙O的一条弦，BD＝4√2，点A是⊙O上的一个动点〔不与点B，D重合〕，以A，B，D为顶点作▱ABCD．〔1〕如图2，假设点A是劣弧BD̂的中点．①求证：▱ABCD是菱形；②求▱ABCD的面积．〔2〕假设点A运动到优弧BD̂上，且▱ABCD有一边与⊙O相切．①求AB的长；②直接写出▱ABCD对角线所夹锐角的正切值．17．〔2021•温州〕如图，在平面直角坐标系中，⊙M经过原点O，分别交x轴、y轴于点A 〔2，0〕，B〔0，8〕，连结AB．直线CM分别交⊙M于点D，E〔点D在左侧〕，交x轴于点C〔17，0〕，连结AE．〔1〕求⊙M的半径和直线CM的函数表达式；〔2〕求点D，E的坐标；〔3〕点P在线段AC上，连结PE．当∠AEP与△OBD的一个内角相等时，求所有满足条件的OP的长．18．〔2021•金华〕在扇形AOB中，半径OA＝6，点P在OA上，连结PB，将△OBP沿PB折叠得到△O′BP．̂所在的圆相切于点B．〔1〕如图1，假设∠O＝75°，且BO′与AB①求∠APO′的度数．②求AP的长．̂相交于点D，假设点D为AB̂的中点，且PD∥OB，求AB̂的长．〔2〕如图2，BO′与AB19．〔2021•丽水〕如图，在△ABC中，AC＝BC，以BC为直径的半圆O交AB于点D，过点D作半圆O的切线，交AC于点E．〔1〕求证：∠ACB＝2∠ADE；̂的长．〔2〕假设DE＝3，AE=√3，求CD̂所对的圆周角，∠ACD＝30°．20．〔2021•湖州〕如图，AB是⊙O的直径，∠ACD是AD〔1〕求∠DAB的度数；〔2〕过点D作DE⊥AB，垂足为E，DE的延长线交⊙O于点F．假设AB＝4，求DF的长．2021年浙江中考数学真题汇编——专题7圆参考答案与试题解析一．选择题〔共7小题〕1．【解答】解：扇形面积=150π×62360=15π，应选：D ． 2．【解答】解：如图，设AB ＝c ，AC ＝b ，BC ＝a ， 那么a 2+b 2＝c 2，① 取AB 的中点为O ， ∵△ABC 是直角三角形， ∴OA ＝OB ＝OC ，∵圆心在MN 和HG 的垂直平分线上， ∴O 为圆心，连接OG ，OE ，那么OG ，OE 为半径， 由勾股定理得：r 2=(a +b 2)2+(a 2)2=c 2+(c 2)2，② 由①②得a ＝b ， ∴a 2=c 22， ∴S 1=54πc 2，∴S 2=12ab =c 24，∴S 1S 2=54πc 2÷c 24=5π，应选：C ．3．【解答】解：连接OB 、OC ，如图，∵正方形ABCD内接于⊙O，∴BC弧所对的圆心角为90°，∴∠BOC＝90°，∴∠BPC=12∠BOC＝45°．应选：B．4．【解答】解：⊙O的半径为2cm，线段OA＝3cm，OB＝2cm，即点A到圆心O的距离大于圆的半径，点B到圆心O的距离等于圆的半径，∴点A在⊙O外，点B在⊙O上，∴直线AB与⊙O的位置关系为相交或相切，应选：D．5．【解答】解：∵AB是⊙O的直径，CD⊥OA，∴CD＝2DE，∵⊙O的半径为m，∠AOD＝∠α，∴DE＝OD•sinα＝m•sinα，∴CD＝2DE＝2m•sinα，应选：B．6．【解答】解：如图，当P与A重合时，点C关于BP的对称点为C′，当P与D重合时，点C关于BP的对称点为C″，∴点P从点A运动到点D，那么线段CC1扫过的区域为：扇形BC'C''和△BCC''，在△BCD中，∵∠BCD＝90°，BC=√3，CD＝1，∴tan∠DBC=√3=√33，∴∠DBC＝30°，∴∠CBC″＝60°，∵BC＝BC''∴△BCC''为等边三角形，∴S扇形BC′C″=120×π×(√3)2360=π，作C''F⊥BC于F，∵△BCC''为等边三角形，∴BF=12BC=√32，∴C''F＝tan60°×√32=32，∴S△BCC''=12×√3×32=3√34，∴线段CC1扫过的区域的面积为：π+3√3 4．应选：B．7．【解答】解：∵点O为△ABC的外心，∠A＝40°，∴∠A=12∠BOC，∴∠BOC＝2∠A＝80°，应选：C．二．填空题〔共5小题〕8．【解答】解：∵PT是⊙O的切线，T为切点，∴OT⊥PT，在Rt△OPT中，OT═1，OP═2，∴PT═√OP2−OT2═√22−12═√3，故：PT═√3．9．【解答】解：如下图，连接OC，OD，OP，∵AC，BD分别与⊙O相切于点C，D，故∠OCP ＝∠ODP ＝90°，又OC ＝OD ，OP ＝OP ，那么Rt △OCP ≌Rt △ODP 〔HL 〕．∵∠CPD ＝120°，∴∠OPC ＝∠OPD ＝60°，∴∠COP ＝∠DOP ＝30°，∴∠COD ＝60°．∴CD ̂的长为l CD ̂=nπr 180=60°×π×6180=2π． 故答案为：2π．10．【解答】解：BC ̂长度=30π⋅12180=2π， 故答案为：2π．11．【解答】解：根据弧长公式可得：l =nπr 180=30⋅π⋅17180=176π． 故答案为：176π．12．【解答】解：∵⊙O 与△OAB 的边AB 相切，∴OB ⊥AB ，∴∠OBA ＝90°，连接OO ′，如图，∵△OAB 绕点B 按顺时针方向旋转得到△O ′A ′B ，∴∠A ＝∠A ′＝25°，∠ABA ′＝∠OBO ′，BO ＝BO ′，∵OB ＝OO ′，∴△OO ′B 为等边三角形，∴∠OBO ′＝60°，∴∠ABA ′＝60°，∴∠OCB ＝∠A +∠ABC ＝25°+60°＝85°．故答案为85．三．解答题〔共8小题〕13．【解答】解：〔1〕证明：连接AD ，如图，∵CA ＝CB ，∴∠CAB ＝∠ABC ．∵AE ⊥AC ，∴∠CAB +∠EAB ＝90°．∵BC 与⊙A 相切于点D ，∴∠ADB ＝90°．∴∠ABD +∠BAD ＝90°．∴∠BAE ＝∠BAD ．在△ABF 和△ABD 中，{AB =AB ∠BAE =∠BAD AF =AD，∴△ABF ≌△ABD 〔SAS 〕．∴∠AFB ＝∠ADB ＝90°．∴BF 是⊙A 的切线．〔2〕由〔1〕得：BF ⊥AE ，∵AC ⊥AE ，∴BF ∥AC ．∴△EFB ∽△EAC ．∴BE CE =BF CA ，∵BE ＝5，CB ＝AC ＝20，∴CE ＝EB +CB ＝20+5＝25，∴525=BF 20．∴BF ＝4．在Rt △BEF 中，EF =√BE 2−BF 2=√52−42=3．14．【解答】解：〔1〕当x ＝3时，点C 和圆心O 重合，此时CE 为半圆O 的半径，∵AB ＝6，∴EC ＝y 1cm ＝3cm ，∴y 1＝3，故答案为：3；〔2〕函数y 的图象如图：由图象得：当0＜x ＜2时，y 1＜y 2，当x ＝2时，y 1＝y 2，当2＜x ＜6时，y 1＞y 2；〔3〕〕连接OD ，作EH ⊥AB 于H ，由〔2〕知时，有EC ＝EB ，∵AC ＝2，AB ＝6cm ，∴OA ＝OD ＝OE ＝OB ＝3cm ，OC ＝1cm ，∵CD ⊥AB ，∴CD =√OD 2−OC 2=2√2，设OH ＝m ，那么CH ＝1+m ，∵EH ⊥AB ，∴EH =√32−m 2=√9−m 2，∵CE ∥AD ，∴∠DAC ＝∠ECH ，∵∠DCA ＝∠EHC ＝90°，∴△DAC ∽△ECH ，∴CD AC =EH CH ，即2√22=√9−m 21+m ， ∴m 1＝1，m 2=−73〔不合题意，舍去〕，∴HB ＝3﹣1＝2，EH =√OE 2−OH 2=2√2，∴EC =√EH 2+CH 2=√8+4=2√3，EB =√EH 2+HB 2=√8+4=2√3， ∴EC ＝EB ．15．【解答】解：〔1〕∵BD 为⊙O 的直径，∴∠BAD ＝90°，∵AÊ=CD ̂， ∴∠ABG ＝∠DBC ＝α，∴∠AGB ＝90°﹣α；〔2〕∵BD 为⊙O 的直径，∴∠BCD＝90°，∴∠BEC＝∠BDC＝90°﹣α，∴∠BEC＝∠AGB，∵∠CEF＝180°﹣∠BEC，∠BGD＝180°﹣∠AGB，∴∠CEF＝∠BGD，又∵CE＝BG，∠ECF＝∠GBD，∴△CFE≌△BDG(ASA)，∴EF＝DG；〔3〕①如图，连接DE，∵BD为⊙O的直径，∴∠A＝∠BED＝90°，在Rt△ABD中，tan∠ADB=√32，AD＝2，∴AB=√32,AD=√3，∵AÊ=CD̂，∴AÊ+DÊ=CD̂+DÊ，即AD̂=CÊ，∴AD＝CE，∵CE＝BG，∴BG＝AD＝2，∵在Rt△ABG中，sin∠AGB=ABBG=√32,∴∠AGB＝60°，AG=12BG＝1，∴EF＝DG＝AD﹣AG＝1，∵在Rt △DEG 中，∠EGD ＝60°，∴EG =12DG =12，DE =√32DG =√32,在Rt △FED 中，DF =√EF 2+DE 2=√72,∴FG +DG +EF =5+√72， ∴△FGD 的周长为5+√72； ②如图，过点C 作CH ⊥BF 于H ，∵△BDG ≌△CFE ，∴BD ＝CF ，∠CFH ＝∠BDA ，∵∠BAD ＝∠CHF ＝90°，∴△BAD ≌△CHF (AAS )，∴FH ＝AD ，∵AD ＝BG ,∴FH ＝BG ,∵∠BCF ＝90°,∴∠BCH +∠HCF ＝90°,∵∠BCH +∠HBC ＝90°,∴∠HCF ＝∠HBC ,∵∠BHC ＝∠CHF ＝90°,∴△BHC ∽△CHF ,∴BH CH =CH FH ,设GH ＝x ,∴BH ＝2﹣x ，∴CH2＝2(2﹣x)，在Rt△GHC中，CG2＝GH2+CH2,∴CG2＝x2+2(2﹣x)＝(x﹣1)2+3，当x＝1时，CG2的最小值为3，∴CG的最小值为√3．16．【解答】〔1〕①证明：∵AD̂=AB̂,∴AD＝AB,∵四边形ABCD是平行四边形，∴四边形ABCD是菱形．②解：连接OA交BD于J,连接OC．∵AD̂=AB̂,∴OA⊥BD,∵四边形ABCD是菱形，∴AC⊥BD,∴A,O,C共线，在Rt△OJD中，DJ＝BJ＝2√2,OD＝3,∴OJ=√OD2−DJ2=√32−(2√2)2=1,∴AJ＝OA＝OJ＝3﹣1＝2,∵四边形ABCD是菱形，∴AJ＝CJ＝2,∴S菱形ABCD=12•AC•BD=12×4×4√2=8√2．〔2〕①解：当CD与⊙O相切时，连接AC交BD于H,连接OH,OD,延长DO交AB于P ,过点A 作AJ ⊥BD 于J ．∵CD 是⊙O 的切线，∴OD ⊥CD ,∵CD ∥AB ,∴DP ⊥AB ,∴P A ＝PB ,∴DB ＝AD ＝4√2,∵四边形ABCD 是平行四边形，∴DH ＝BH ＝2√2,∴OH ⊥BD ,∴∠DHO ＝∠DPB ＝90°,∵∠ODH ＝∠BDP ,∴△DHO ∽△DPB ,∴DH DP =DO DB =OH PB ,∴2√2DP =4√2=1PB, ∴DP =163,PB =4√23, ∴AB ＝2PB =8√23,当BC 与⊙O 相切时，同法可证AB ＝BD ＝4√2．综上所述，AB 的长为4√2或8√23． ②解：如图3﹣1中，过点A 作AJ ⊥BD 于J ．∵12•AB •DP =12•BD •AJ , ∴AJ =329,∴BJ =√AB 2−AJ 2=(8√23)2−(329)2=8√29, ∴JH ＝BH ＝BJ ＝2√2−8√29=10√29, ∴tan ∠AHJ =AJ HJ =32910√29=8√25, 如图3﹣2中，同法可得▱ABCD 对角线所夹锐角的正切值为8√25，综上所述，▱ABCD 对角线所夹锐角的正切值为8√25， 17．【解答】解：〔1〕∵点M 是AB 的中点，那么点M 〔1,4〕， 那么圆的半径为AM =√(2−1)2+42=√17，设直线CM 的表达式为y ＝kx +b ，那么{17k +b =0k +b =4，解得{k =−14b =174， 故直线CM 的表达式为y =−14x +174；〔2〕设点D 的坐标为〔x ，−14x +174〕，由AM =√17得：〔x ﹣1〕2+〔−14x +174−4〕2＝〔√17〕2，解得x ＝5或﹣3，故点D 、E 的坐标分别为〔﹣3,5〕、〔5,3〕；〔3〕过点D 作DH ⊥OB 于点H ，那么DH ＝3，BH ＝8﹣5＝3＝DH ， 故∠DBO ＝45°，由点A 、E 的坐标，同理可得∠EAP ＝45°；由点A 、E 、B 、D 的坐标得，AE =√(5−2)2+(0−3)2=3√2， 同理可得：BD ＝3√2，OB ＝8，①当∠AEP ＝∠DBO ＝45°时，那么△AEP 为等腰直角三角形，EP ⊥AC ，故点P 的坐标为〔5,0〕，故OP ＝5；②∠AEP ＝∠BDO 时，∵∠EAP ＝∠DBO ，∴△EAP ∽△DBO ，∴AE BD =AP BO ，即√23√2=APBO =AP8，解得AP ＝8，故PO ＝10；③∠AEP ＝∠BOD 时，∵∠EAP ＝∠DBO ， ∴△EAP ∽△OBD ，∴AE OB =APBD ，即3√28=3√2，解得AP =94， 那么PO ＝2+94=174， 综上，OP 为5或10或174．18．【解答】解：〔1〕①如图1中，∵BO′是⊙O的切线，∴∠OBO′＝90°,由翻折的性质可知，∠OBP＝∠PBO′＝45°,∠OPB＝∠BPO′,∵∠AOB＝75°,∴∠OPB＝∠BPO′＝180°﹣75°﹣45°＝60°,∴∠OPO′＝120°,∴∠APO′＝180°﹣∠OPO′＝180°﹣120°＝60°．②如图1中，过点B作BH⊥OA于H,在BH上取一点F,使得OF＝FB,连接OF．∵∠BHO＝90°,∴∠OBH＝90°﹣∠BOH＝15°,∵FO＝FB,∴∠FOB＝∠FBO＝15°,∴∠OFH＝∠FOB+∠FBO＝30°,设OH＝m,那么HF=√3m,OF＝FB＝2m,∵OB2＝OH2+BH2,∴62＝m2+(√3m+2m)2,∴m=3√6−3√22或−3√6−3√22〔舍弃〕，∴OH=3√6−3√22,BH=3√2+3√62,在Rt△PBH中，PH=BHtan60°=√6+3√22,∴P A＝OA﹣OH﹣PH＝6−3√6−3√22−√6+3√22=6﹣2√6．(2)如图2中，连接AD,OD．∵AD̂=BD̂,∴AD＝BD,∠AOD＝∠BOD,由翻折的旋转可知，∠OBP＝∠PBD,∵PD∥OB,∴∠DPB＝∠OBP,∴∠DPB ＝∠PBD ,∴DP ＝DB ＝AD ,∴∠DAP ＝∠APD ＝∠AOB ,∵AO ＝OD ＝OB ,AD ＝DB ,∴△AOD ≌△BOD ,∴∠OBD ＝∠OAD ＝∠AOB ＝2∠BOD ,∵OB ＝OD ,∴∠OBD ＝∠ODB ＝2∠DOB ,∴∠DOB ＝36°,∴∠AOB ＝72°，∴AB ̂的长=72π⋅6180=12π5。

三年（2019-2021）中考真题数学分项汇编（浙江专用）专题14圆（解答题）一．解答题（共20小题）1．（2021•丽水）如图，在△ABC中，AC＝BC，以BC为直径的半圆O交AB于点D，过点D作半圆O的切线，交AC于点E．（1）求证：∠ACB＝2∠ADE；̂的长．（2）若DE＝3，AE=√3，求CD【分析】（1）连接OD，CD，根据切线的性质得到∠ODE＝90°，根据圆周角定理得到∠BDC＝90°，求得∠ADE＝∠ODC，根据等腰三角形的性质即可得到结论；（2）根据勾股定理得到AD=√32+(√3)2=2√3，tan A=√3，求得∠A＝60°，推出△ABC是等边三角形，得到∠B＝60°，BC＝AB＝2AD＝4√3，根据弧长公式即可得到结论．【详解】（1）证明：连接OD，CD，∵DE是⊙O的切线，∴∠ODE＝90°，∴∠ODC+∠EDC＝90°，∵BC为⊙O直径，∴∠BDC＝90°，∴∠ADC＝90°，∴∠ADE+∠EDC＝90°，∴∠ADE＝∠ODC，∵AC＝BC，∴∠ACB＝2∠DCE＝2∠OCD，∵OD＝OC，∴∠ODC ＝∠OCD ，∴∠ACB ＝2∠ADE ；（2）解：由（1）知，∠ADE +∠EDC ＝90°，∠ADE ＝∠DCE ，∴∠AED ＝90°，∵DE ＝3，AE =√3，∴AD =√32+(√3)2=2√3，tan A =√3，∴∠A ＝60°，∵AC ＝BC ，∴△ABC 是等边三角形，∴∠B ＝60°，BC ＝AB ＝2AD ＝4√3，∴∠COD =2∠B =120°，OC =2√3，∴CD ̂ 的长为nπr 180=120⋅π×2√3180=4√3π3．2．（2021•湖州）如图，已知AB 是⊙O 的直径，∠ACD 是AD̂所对的圆周角，∠ACD ＝30°． （1）求∠DAB 的度数；（2）过点D 作DE ⊥AB ，垂足为E ，DE 的延长线交⊙O 于点F ．若AB ＝4，求DF 的长．【分析】（1）连接BD ，根据AB 是⊙O 的直径，可得∠ADB ＝90°，进而可以求∠DAB 的度数；（2）根据直角三角形30度角所对直角边等于斜边的一半可得AD 的长，再根据垂径定理和特殊角三角函数值可得EF ＝DE 的值，进而可得DF 的长．【详解】解：（1）如图，连接BD ，∵∠ACD＝30°，∴∠B＝∠ACD＝30°，∵AB是⊙O的直径，∴∠ADB＝90°，∴∠DAB＝90°﹣∠B＝60°；（2）∵∠ADB＝90°，∠B＝30°，AB＝4，∴AD=12AB＝2，∵∠DAB＝60°，DE⊥AB，且AB是直径，∴EF＝DE＝AD sin60°=√3，∴DF＝2DE＝2√3．3．（2021•金华）在扇形AOB中，半径OA＝6，点P在OA上，连结PB，将△OBP沿PB折叠得到△O′BP．（1）如图1，若∠O＝75°，且BO′与AB̂所在的圆相切于点B．①求∠APO′的度数．②求AP的长．（2）如图2，BO′与AB̂相交于点D，若点D为AB̂的中点，且PD∥OB，求AB̂的长．【分析】（1）①利用三角形内角和定理求解即可。

考点23圆的有关性质考点总结1.圆的有关概念(1)圆：平面上到定点的距离等于定长的所有点组成的图形叫做圆，定点叫做圆心，定长叫做圆的半径．以点O为圆心的圆，记做⊙O．(2)弧和弦：圆上任意两点间的部分叫做圆弧，简称弧．连结圆上任意两点的线段叫做弦．经过圆心的弦叫做直径，直径是圆中最长的弦．(3)与圆有关的角：①圆心角：顶点在圆心的角叫做圆心角，圆心角的度数等于它所对的弧的度数．②圆周角：顶点在圆上，两边分别和圆相交的角叫做圆周角．圆周角的度数等于它所对弧上的圆心角度数的一半．(4)三角形的外心：三角形外接圆的圆心叫做三角形的外心．外心也是三角形三边中垂线的交点．(5)圆的内接四边形：如果一个四边形的各个顶点在同一个圆上，那么这个四边形叫做圆的内接四边形，这个圆叫做四边形的外接圆．圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角．2．圆的有关性质：(1)圆是轴对称图形，其对称轴是任意一条过圆心的直线．圆是中心对称图形，对称中心为圆心，圆绕着它的圆心旋转任意一个角度都能和原来的圆重合．(2)垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．推论1：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧．推论2：平分弧的直径垂直平分弧所对的弦．(3)在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等，那么它们所对应的其余各组量都相等．(4)圆心角与圆周角的关系：一条弧所对的圆周角等于它所对的圆心角的一半．推论1：在同圆或等圆中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等．推论2：半圆(或直径)所对的圆周角是直角，90°的圆周角所对的弦是直径．(5)确定圆的条件：①已知圆心、半径；②已知直径；③不在同一条直线上的三点．真题演练一、单选题1．（2021·浙江衢州·中考真题）已知扇形的半径为6，圆心角为150︒．则它的面积是（ ）A ．32π B ．3π C ．5π D ．15π【答案】D【分析】 已知扇形的半径和圆心角度数求扇形的面积，选择公式2360n R S π=直接计算即可． 【详解】 解：2150615360S ππ⨯==． 故选：D2．（2021·浙江嘉兴·中考真题）如图，在ABC ∆中，90BAC ∠=︒，AB =AC =5，点D 在AC 上，且2AD =，点E 是AB 上的动点，连结DE ，点F ，G 分别是BC ，DE 的中点，连接AG ，FG ，当AG =FG 时，线段DE 长为（ ）A B C D ．4【答案】A【分析】连接DF ，EF ，过点F 作FN ⊥AC ，FM ⊥AB ，结合直角三角形斜边中线等于斜边的一半求得点A ，D ，F ，E 四点共圆，⊥DFE =90°，然后根据勾股定理及正方形的判定和性质求得AE 的长度，从而求解．【详解】解：连接DF ，EF ，过点F 作FN ⊥AC ，FM ⊥AB⊥在ABC ∆中，90BAC ∠=︒，点G 是DE 的中点，⊥AG =DG =EG又⊥AG =FG⊥点A ，D ，F ，E 四点共圆，且DE 是圆的直径⊥⊥DFE =90°⊥在Rt ⊥ABC 中，AB =AC =5，点F 是BC 的中点，⊥CF =BF =122BC =，FN =FM =52 又⊥FN ⊥AC ，FM ⊥AB ，90BAC ∠=︒⊥四边形NAMF 是正方形⊥AN =AM =FN =52又⊥90NFD DFM ∠+∠=︒，90DFM MFE ∠+∠=︒⊥NFD MFE ∠=∠⊥⊥NFD ⊥⊥MFE⊥ME =DN =AN -AD =12⊥AE =AM +ME =3⊥在Rt ⊥DAE 中，DE故选：A ．3．（2021·浙江·中考真题）如图，已知点O 是ABC 的外心，∠40A =︒，连结BO ，CO ，则BOC ∠的度数是（ ）．A ．60︒B ．70︒C ．80︒D ．90︒【答案】C【分析】 结合题意，根据三角形外接圆的性质，作O ；再根据圆周角和圆心角的性质分析，即可得到答案．【详解】 ABC 的外接圆如下图⊥⊥40A =︒⊥280BOC A ∠=∠=︒故选：C ．4．（2021·浙江·中考真题）如图，已知在矩形ABCD 中，1,AB BC ==P 是AD 边上的一个动点，连结BP ，点C 关于直线BP 的对称点为1C ，当点P 运动时，点1C 也随之运动．若点P 从点A 运动到点D ，则线段1CC 扫过的区域的面积是（ ）A ．πB ．π+CD ．2π【答案】B【分析】先判断出点Q 在以BC 为直径的圆弧上运动，再判断出点C 1在以B 为圆心，BC 为直径的圆弧上运动，找到当点P 与点A 重合时，点P 与点D 重合时，点C 1运动的位置，利用扇形的面积公式及三角形的面积公式求解即可．【详解】解：设BP 与CC 1相交于Q ，则⊥BQC =90°，⊥当点P 在线段AD 运动时，点Q 在以BC 为直径的圆弧上运动，延长CB 到E ，使BE =BC ，连接EC ，⊥C 、C 1关于PB 对称，⊥⊥EC 1C =⊥BQC =90°，⊥点C 1在以B 为圆心，BC 为直径的圆弧上运动，当点P 与点A 重合时，点C 1与点E 重合，当点P 与点D 重合时，点C 1与点F 重合，此时，tanPC AB PBC BC BC ∠=== ⊥⊥PBC =30°，⊥⊥FBP =⊥PBC =30°，CQ =12BC =BQ 32=，⊥⊥FBE =180°-30°-30°=120°，11322BCF S CC BQ =⨯==线段1CC 扫过的区域的面积是2120360BCF S ππ⨯+= 故选：B ． 5．（2021·浙江丽水·中考真题）如图，AB 是O 的直径，弦CD OA ⊥于点E ，连结,OC OD ．若O 的半径为,m AOD α∠=∠，则下列结论一定成立的是（ ）A ．tan OE m α=⋅B ．2sin CD m α=⋅C ．cos AE m α=⋅D ．2sin COD S m α=⋅【答案】B【分析】 根据垂径定理、锐角三角函数的定义进行判断即可解答．【详解】解：⊥AB 是O 的直径，弦CD OA ⊥于点E ， ⊥12DE CD = 在Rt EDO ∆中，OD m =，AOD α∠=∠ ⊥tan =DE OE α ⊥=tan 2tan DE CD OE αα=，故选项A 错误，不符合题意； 又sin DE OD α=⊥sin DE OD α=⊥22sin CD DE m α==，故选项B 正确，符合题意； 又cos OE ODα= ⊥cos cos OE OD m αα==⊥AO DO m ==⊥cos AE AO OE m m α=-=-，故选项C 错误，不符合题意；⊥2sin CD m α=，cos OE m α=⊥2112sin cos sin cos 22COD S CD OE m m m αααα∆=⨯=⨯⨯=，故选项D 错误，不符合题意；故选B ．6．（2021·浙江金华·中考真题）如图，在Rt ABC 中，90ACB ∠=︒，以该三角形的三条边为边向形外作正方形，正方形的顶点,,,,,E F G H M N 都在同一个圆上．记该圆面积为1S ，ABC 面积为2S ，则12S S 的值是（ ）A ．52πB ．3πC ．5πD ．112π 【答案】C【分析】先确定圆的圆心在直角三角形斜边的中点，然后利用全等三角形的判定和性质确定⊥ABC 是等腰直角三角形，再根据直角三角形斜边中线的性质得到2214S AB =，再由勾股定理解得2254OF AB =，解得2154S AB π=⋅，据此解题即可． 【详解】 解：如图所示，正方形的顶点,,,,,E F G H M N 都在同一个圆上，∴圆心O 在线段,EF MN 的中垂线的交点上，即在Rt ABC 斜边AB 的中点，且AC =MC ，BC =CG ，⊥AG =AC +CG =AC +BC ，BM =BC +CM =BC +AC ，⊥AG =BM ，又⊥OG =OM ，OA =OB ，⊥⊥AOG ⊥⊥BOM ，⊥⊥CAB =⊥CBA ，⊥⊥ACB =90°，⊥⊥CAB =⊥CBA =45°，12OC AB ∴=， 2211112224S AB OC AB AB AB ∴=⋅=⋅= 22222215()24OF AO AF AB AB AB =+=+= 22154S OF AB ππ∴==⋅， 212254514AB S S AB ππ⋅∴==．故选：C ．7．（2021·浙江绍兴·中考真题）如图，正方形ABCD 内接于O ，点P 在AB 上，则P ∠的度数为（ ）A ．30B ．45︒C ．60︒D ．90︒【答案】B【分析】 连接OB ，OC ，由正方形ABCD 的性质得90BOC ∠=°，再根据圆周角与圆心角的关系即可得出结论．【详解】解：连接OB ，OC ，如图，⊥正方形ABCD 内接于O ，⊥90BOC ∠=° ⊥11904522BPC BOC ∠=∠=⨯︒=︒ 故选：B ．8．（2021·浙江嘉兴·中考真题）已知平面内有O 和点A ，B ，若O 半径为2cm ，线段3cm OA =，2cm OB =，则直线AB 与O 的位置关系为（ ）A ．相离B ．相交C ．相切D ．相交或相切【答案】D【分析】根据点与圆的位置关系的判定方法进行判断．【详解】解：⊥⊥O 的半径为2cm ，线段OA =3cm ，线段OB =2cm ，即点A 到圆心O 的距离大于圆的半径，点B 到圆心O 的距离等于圆的半径， ⊥点A 在⊥O 外．点B 在⊥O 上，⊥直线AB 与⊥O 的位置关系为相交或相切，故选：D ．9．（2021·浙江·杭州市丰潭中学二模）如图，已知平面直角坐标系中，点A ，B 坐标分别为A （4，0），B （﹣6，0）．点C 是y 轴正半轴上的一点，且满足∠ACB ＝45°，圆圆得到了以下4个结论：∠∠ABC 的外接圆的圆心在OC 上；∠∠ABC ＝60°；∠∠ABC的外接圆的半径等于∠OC ＝12．其中正确的是（ ）A ．∠∠B ．∠∠C ．∠∠D ．∠∠【答案】C【分析】 如图，作出ABC 的外接圆，以AB 为斜边在x 轴上方作等腰Rt ABE △，过点E 作ED x ⊥轴于D ，连接EC ，过点E 作EF y ⊥轴于F ，由圆心必然在弦的垂直平分线上可判断⊥；再证明E 为ABC 外接圆圆心，求出半径，可判断⊥；再在ECF △中由勾股定理求出CF ，可求得OC 和1tan 2OC ABC OB ∠==，即可判断⊥⊥． 【详解】解：如图，作出ABC 的外接圆，以AB 为斜边在x 轴上方作等腰Rt ABE △， 过点E 作ED x ⊥轴于D ，连接EC ，过点E 作EF y ⊥轴于F ，⊥ABC 的外接圆的圆心必在弦AB 的垂直平分线上，⊥圆心肯定不在OC 上，故⊥错误；⊥⊥ACB ＝45°，⊥由圆周角定理得：AB 所对的圆心角必为90°，⊥EB ＝EA ，⊥在弦AB 的垂直平分线上，⊥⊥AEB ＝90°，⊥E 必为圆心，即AE 、BE 为半径， ⊥AE =⊥正确；⊥BD ＝5，OB ＝6，⊥OD ＝1，⊥⊥EDO ＝⊥DOF ＝⊥OFE ＝90°，⊥OD ＝EF ＝1，ED ＝FO ＝5，⊥7CF ==，⊥OC ＝OF +FC ＝12，故⊥正确；⊥1 tan2OCABCOB∠==，⊥⊥ABC≠60°，故⊥错误；故选：C．10．（2021·浙江·杭州市丰潭中学二模）如图，点A的坐标为（﹣3，2），∠A的半径为1，P为坐标轴上一动点，PQ切∠A于点Q，在所有P点中，使得PQ长最小时，点P 的坐标为（）A．（0，2）B．（0，3）C．（﹣2，0）D．（﹣3，0）【答案】D【分析】连接AQ、P A，如图，利用切线的性质得到⊥AQP=90°，再根据勾股定理得到PQ=AP⊥x轴时，AP的长度最小，利用垂线段最短可确定P点坐标．【详解】解：连接AQ、P A，如图，⊥PQ切⊥A于点Q，⊥AQ⊥PQ，⊥⊥AQP＝90°，⊥PQ当AP的长度最小时，PQ的长度最小，⊥AP⊥x轴时，AP的长度最小，⊥AP⊥x轴时，PQ的长度最小，二、填空题11．（2021·浙江杭州·中考真题）如图，已知O 的半径为1，点P 是O 外一点，且2OP =．若PT 是O 的切线，T 为切点，连接OT ，则PT =_____．【分析】根据圆的切线的性质，得90OTP ∠=︒，根据圆的性质，得1OT =，再通过勾股定理计算，即可得到答案．【详解】⊥PT 是O 的切线，T 为切点⊥90OTP ∠=︒⊥PT⊥O 的半径为1⊥1OT =⊥PT12．（2021·浙江台州·中考真题）如图，将线段AB 绕点A 顺时针旋转30°，得到线段AC ．若AB ＝12，则点B 经过的路径BC 长度为_____．（结果保留π）直接利用弧长公式即可求解．【详解】 解：30122180BC l ππ⋅==， 故答案为：2π．13．（2021·浙江温州·中考真题）图1是邻边长为2和6的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图2），则图1中所标注的d 的值为______；记图1中小正方形的中心为点A ，B ，C ，图2中的对应点为点A '，B '，C '．以大正方形的中心O 为圆心作圆，则当点A '，B '，C '在圆内或圆上时，圆的最小面积为______．【答案】6- (16π-【分析】（1）先求出剪拼后大正方形的面积，得到其边长，再结合图2，求出图1中长方形的长边除去长为d 部分的线段后，剩下的线段长刚好为大正方形的边长，最后用图1中的长方形的长减去图2中大正方形的边长即可完成求解；（2）结合两图分别求出对应线段的长，通过作辅助线构造直角三角形，利用勾股定理求出O 点到'B 、'A 、'C 之间的距离即可确定最小圆的半径，即可完成求解．【详解】解：⊥图1是邻边长为2和6的矩形，它由三个小正方形组成，⊥每个小正方形边长为2，图1和图2中整个图形的面积为2612=⨯，所以图2中正方形的边长''M N =如下图3所示；分别连接'OB 、'OA 、'OC ，并分别过点'B 、'A 、'C 向大正方形的对边作垂线，得到如图所示辅助线，综合两图可知，'1LA =,LJ ='1MA =,O⊥'1JA =，1OJ =,⊥)'1OA ===综合两图可知：'1B E =,6'32B D d =-=,DF =⊥()''33B F DF B D =-==1OF =,⊥'OB =；继续综合两图可知：''1C H C G ==,⊥'1C I OI =,⊥'OC =⊥2816=-<-⊥'B 距离O 点最远，⊥⊥圆的面积为(16π-；故答案为：6-(16π-．14．（2021·浙江宁波·中考真题）抖空竹在我国有着悠久的历史，是国家级的非物质文P ．若120P ∠=︒，O 的半径为6cm ，则图中CD 的长为________cm ．（结果保留π）【答案】2π【分析】连接OC 、OD ，利用切线的性质得到90OCP ODP ∠=∠=︒，根据四边形的内角和求得60COD ∠=︒，再利用弧长公式求得答案．【详解】连接OC 、OD ，⊥,AC BD 分别与O 相切于点C ，D ，⊥90OCP ODP ∠=∠=︒，⊥120P ∠=︒，360OCP ODP P COD ∠+∠+∠+∠=︒，⊥60COD ∠=︒，⊥CD 的长=6062180（cm ），故答案为：2π．．15．（2021·浙江温州·中考真题）如图，O 与OAB 的边AB 相切，切点为B ．将OAB 绕点B 按顺时针方向旋转得到O A B '''△，使点O '落在O 上，边A B '交线段AO 于点C ．若25A '∠=︒，则OCB ∠=______度．【答案】85AB 相切，可求⊥CBO ==30°，利用三角形内角和公式即可求解．【详解】解：连结OO′，⊥将OAB 绕点B 按顺时针方向旋转得到O A B '''△，⊥BO′=BO =OO′，⊥⊥BOO′为等边三角形，⊥⊥OBO′=60°，⊥O 与OAB 的边AB 相切，⊥⊥OBA =⊥O′BA′=90°，⊥⊥CBO =90°-⊥OBO′=90°-60°=30°，⊥⊥A′=25°⊥⊥A′O′B =90°-⊥A′=90°-25°=65°⊥⊥AOB =⊥A′O′B =65°，⊥⊥OCB =180°-⊥COB -⊥OBC =180°-65°-30°=85°．故答案为85．三、解答题16．（2021·浙江衢州·中考真题）如图，在ABC 中，CA CB =，BC 与A 相切于点D ，过点A 作AC 的垂线交CB 的延长线于点E ，交A 于点F ，连结BF ．（1）求证：BF 是A 的切线．【答案】（1）见解析；（2）3【分析】（1）连接AD ，根据题意证明ABF ABD △△≌，即可证明BF 是A 的切线；（2）根据题意即（1）的结论可得BEF CEA △∽△，列比例求出FB 的长，根据勾股定理求EF 即可．【详解】（1）证明如图，连接AD ，CA CB =，CAB ABC ∴∠=∠，AE AC ⊥，90CAB EAB ∴∠+∠=︒又A 切BC 于点D ，=90ADB ∴∠︒，90ABD BAD ∴∠+∠=︒，BAE BAD ∴∠=∠．又AB AB ，AF AD =，()ABF ABD SAS ∴△△≌，90AFB ADB ∴∠=∠=︒，BF ∴是A 的切线．（2）由（1）得：90AFB FAC ∠=∠=︒，//BF AC ∴，BEF CEA ∴△∽△，BE BF CE CA∴=， 20CB CA ==，5BE =，∴=．EF317．（2021·浙江台州·中考真题）如图，BD是半径为3的∠O的一条弦，BD＝点A是∠O上的一个动点（不与点B，D重合），以A，B，D为顶点作平行四边形ABCD．（1）如图2，若点A是劣弧BD的中点．∠求证：平行四边形ABCD是菱形；∠求平行四边形ABCD的面积．（2）若点A运动到优弧BD上，且平行四边形ABCD有一边与∠O相切．∠求AB的长；∠直接写出平行四边形ABCD对角线所夹锐角的正切值．【答案】⊥证明见解析；⊥（2）⊥AB【分析】（1）⊥利用等弧所对的弦相等可得AD AB=，根据一组邻边相等的平行四边形是菱形可得证；⊥连接AO，交BD于点E，连接OD，根据垂径定理可得DE BE==用勾股定理求出OE的长，即可求解；（2）⊥分情况讨论当CD与O相切时、当BC与O相切时，利用垂径定理即可求解；⊥根据等面积法求出AH的长度，利用勾股定理求出DH的长度，根据正切的定义即可求解．【详解】解：（1）⊥⊥点A是劣弧BD的中点，⊥四边形ABCD 是平行四边形，⊥平行四边形ABCD 是菱形；⊥连接AO ，交BD 于点E ，连接OD ，，⊥点A 是劣弧BD 的中点，OA 为半径，⊥OA BD ⊥，OA 平分BD ， ⊥DE BE ==⊥平行四边形ABCD 是菱形，⊥E 为两对角线的交点，在Rt ODE △中，1OE ,⊥2AE =，⊥122ABCD S BD AE =⋅⨯= （2）⊥如图，当CD 与O 相切时，连接DO 并延长，交AB 于点F ，⊥CD 与O 相切，⊥DF CD ⊥，⊥四边形ABCD 是平行四边形，⊥//AB CD ，⊥DF AB ⊥，在Rt BDF △中，()2222323BF BD DF OF =-=-+， 在Rt BOF △中，22229BF BO OF OF =-=-，⊥()223239OF OF -+=-，解得73OF =，⊥BF =⊥2AB BF = 如图，当BC 与O 相切时，连接BO 并延长，交AD 于点G ，同理可得AG DG =73OG =，所以AB综上所述，AB ⊥过点A 作AH BD ⊥，，由（2）得：7163,33BD AD BG ==+= 根据等面积法可得1122BD AH AD BG ⋅=⋅， 解得329AH =，在在Rt ADH 中，DH ==⊥HI =⊥tan AH AIH HI ∠== 18．（2021·浙江金华·中考真题）在扇形AOB 中，半径6OA =，点P 在OA 上，连结PB ，将OBP 沿PB 折叠得到O BP '．（1）如图1，若75O ∠=︒，且BO '与AB 所在的圆相切于点B ．∠求APO ∠'的度数．∠求AP 的长．（2）如图2，BO '与AB 相交于点D ，若点D 为AB 的中点，且//PD OB ，求AB 的长．【答案】（1）⊥60°；⊥6-（2）125π 【分析】(1)根据图像折叠的性质，确定角之间的关系，通过已知的角度来间接求所求角的角度；求AP 的长，先连接'OO ，先在Rt OBQ △中，求出OQ ；再在Rt OPQ 中，求出OP 即可得到答案；（2）要求AB 的长，扇形的半径已知，就转化成求AOB ∠的度数，连接'OO ，通过条件找到角之间的等量关系，再根据三角形内角和为180︒，建立等式求出AOB ∠，最后利用弧长的计算公式进行计算．【详解】解：（1）⊥如图1，'BO 为圆的切线'90OBO ∴∠=︒．由题意可得，'45O BP OBP ∠=∠=︒，'O PB OPB ∠=∠．180180754560OPB BOP OBP ∴∠=︒-∠-∠=︒-︒-︒=︒ '60O PB OPB ∴∠=∠=︒'60APO ∴∠=︒，⊥如图1，连结'OO ，交BP 于点Q ．则有'BP OO ⊥．在Rt OBQ △中，sin 45OQ OB =⨯︒=在Rt OPQ △中，sin 60OQ OP ==︒6AP OA OP ∴=-=-（2）如图2．连结OD ．设1a ∠=．⊥点D 为AB 的中点．BD AD ∴=21a ∴∠=∠=//PD OB321a ∴∠=∠=∠=．PD PO ∴=由题意可得，','PO PO O BOP =∠=∠．'PD PO ∴=''2PDO O BOP a ∴∠=∠=∠=又//,''2PD OB OBO PDO a ∴∠=∠=,4'2OB OD OBO a =∴∠=∠=43'180PDO ∠+∠+∠=︒，22180a a a ∴++=︒，解得36a =︒． 72AOB ∴∠=︒726121801805n R AB πππ⨯∴===．。

备战中考数学（浙教版）巩固复习圆的基本性质（含解析）A. cmB.C.D. 1cm4.如图，AB是⊙O的直径，弦BC＝2cm，F是弦BC的中点，∠ABC＝60°．若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动，设运动时间为t(s)(0≤t＜3)，连接EF，当△BEF是直角三角形时，t(s)的值为( )A.B. 1C. 或1D. 或1或5.若正多边形的一个外角为60°，则这个正多边形的中心角的度数是（）A. 30°B. 60°C. 90°D. 120°6.下列结论错误的是（）A. 圆是轴对称图形B. 圆是中心对称图形C. 半圆不是弧 D. 同圆中，等弧所对的圆心角相等7.如图，在半圆的直径上作4个正三角形，如这半圆周长为C1，这4个正三角形的周长和为C2，则C1和C2的大小关系是（）A. C1＞C2B. C1＜C2C. C1=C2D. 不能确定8.如图，三角形ABC内接于圆O，AH BC于点H，若AC=8，AH=6，圆O的半径OC=5，则AB的值为（）.A. 5B.C. 7D.9.下列结论正确的是（）A. 经过圆心的直线是圆的对称轴B. 直径是圆的对称轴C. 与圆相交的直线是圆的对称轴D. 与直径相交的直线是圆的对称轴10.如图，D是弧AC的中点，则图中与∠ABD相等的角的个数是( )A. 4个B. 3个C. 2个D. 1个11.如图，AB为⊙O的直径，点C在⊙O上，若∠C=15°，则∠BOC =（）.A. 60°B. 45°C. 30°D. 15°二、填空题12.如图，在半径为4cm的⊙O中，劣弧AB的长为2πcm，则∠C=________ 度．13.如图，三角板ABC中，∠ACB=90°，∠B=30°，AC=2，三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则点B转过的路径长为________ （结果保留π）．14.已知扇形的半径为3，扇形的圆心角是120°，则该扇形面积为________．15.如图，A、B、C、D是圆上的点，∠1=70°，∠A=40°则∠C=________度．16.已知扇形的圆心角为120°，弧长等于一个半径为5cm的圆的周长，则扇形的面积为________．17.如图，半径为2的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是________.18.如图，点A、B、C在⊙O上，∠A=50°，则∠BOC度数为________ ．19.已知正六边形的边心距为，则这个正六边形的边长为________ ．三、解答题20.“不在同一直线上的三点确定一个圆”．请你判断平面直角坐标系内的三个点A(2，3)，B(－3，－7)，C(5，11)是否可以确定一个圆．21如图，BM是⊙O的直径，四边形ABMN是矩形，D是⊙O上的点，DC⊥AN，与AN交于点C，己知AC=15，⊙O的半径为30，求的长．四、综合题22.已知点在⊙ 上，，仅使用无刻度的直尺作图（保留痕迹）（1）在图①中画一个含的直角三角形；（2）点在弦上，在图②中画一个含的直角三角形.答案解析部分一、单选题1.【答案】A【考点】弧长的计算【解析】【解答】解：∵l=，∴r==18，故选A．【分析】根据弧长公式l=进行计算即可．2.【答案】D【考点】点与圆的位置关系【解析】【解答】设以QP为直径的圆为⊙O，则⊙O的半径为QP，如果OA＞QP，那么点A在⊙O外；如果OA＝QP，那么点A在⊙O上；如果OA＜QP，那么点A在⊙O内；∵题目没有告诉OA与QP的大小关系，∴以上三种情况都有可能.故选D.【分析】设以QP为直径的圆为⊙O，要判断点A 与此圆的位置关系，只需比较OA与⊙O的半径大小即可.3.【答案】A【考点】正多边形和圆【解析】【解答】连接AC ，过B作BD⊥AC于D；∵AB=BC，∴△ABC是等腰三角形，∴AD=CD；∵此多边形为正六边形，∴∴∠ABD= =60°∴∠BAD=30°，AD=AB·cos30°=∴a= cm故选A【分析】连接AC，作BD⊥AC于D；根据正六边形的特点求出∠ABC的度数，再由等腰三角形的性质求出∠BAD的度数，由特殊角的三角函数值求出AD的长，进而可求出AC的长．4.【答案】D【考点】圆周角定理【解析】【分析】若△BEF是直角三角形，则有两种情况：①∠BFE=90°，②∠BEF=90°；在上述两种情况所得到的直角三角形中，已知了BC边和∠B的度数，即可求得BE的长；AB的长易求得，由AE=AB-BE即可求出AE的长，也就能得出E点运动的距离，根据时间=路程÷速度即可求得t的值．【解答】∵AB是⊙O的直径，∴∠ACB=90°；Rt△ABC中，BC=2，∠ABC=60°；∴AB=2BC=4cm；①当∠BFE=90°时；Rt△BEF中，∠ABC=60°，则BE=2BF=2cm；故此时AE=AB-BE=2cm；∴E点运动的距离为：2cm，故t=1s；所以当∠BFE=90°时，t=1s；②当∠BEF=90°时；同①可求得BE=0.5cm，此时AE=AB-BE=3.5cm；∴E点运动的距离为：3.5cm，故t=1.75s；③当E从B回到O的过程中，在运动的距离是：2（4-3.5)=1cm，则时间是：1.75+=．综上所述，当t的值为1s或1.75s和s时，△BEF是直角三角形．故选：D．【点评】此题主要考查了圆周角定理以及直角三角形的判定和性质，同时还考查了分类讨论的数学思想5.【答案】B【考点】正多边形和圆【解析】【解答】解：∵正多边形的一个外角为60°，∴正多边形的边数为=6，其中心角为=60°．故选B．【分析】根据正多边形的外角和是360°求出正多边形的边数，再求出其中心角．6.【答案】C【考点】圆的认识【解析】【解答】A、圆是轴对称图形，说法正确；B、圆是中心对称图形，说法正确；C、半圆不是弧，说法错误；D、同圆中，等弧所对的圆心角相等，说法正确；故选：C【分析】根据圆既是轴对称图形，也是中心对称图形，圆上任意两点间的部分叫圆弧，简称弧，圆的任意一条直径的两个端点把圆分成两条弧，每条弧都叫做半圆，大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧，进行分析．7.【答案】B【考点】圆的认识【解析】【解答】解：设半圆的直径为a，则半圆周长C1为：aπ+a，4个正三角形的周长和C2为：3a，∵aπ+a＜3a，∴C1＜C2故选B．【分析】首先设出圆的直径，然后表示出半圆的周长与三个正三角形的周长和，比较后即可得到答案．8.【答案】D【考点】三角形的外接圆与外心【解析】试题分析：作直径AE，连接CE，∴∠ACE=90°，∵AH⊥BC，∴∠AHB=90°，∴∠ACE=∠ADB，∵∠B=∠E，∴△ABH∽△AEC，∴ ，∴AB= ，∵AC=24，AH=18，AE=2OC=26，∴AB=故选：D．9.【答案】A【考点】圆的认识【解析】【解答】A、经过圆心的直线是圆的对称轴，所以A正确；B、直径所在的直线为圆的对称轴，所以B错误；C、与圆相交的直线不一定是圆的对称轴，所以C错误；D、与直径相交的圆心的直线是圆的对称轴，所以D错误．故选A．【分析】利用直径所在的直线为圆的对称轴对各选项进行判断．10.【答案】B【考点】圆周角定理【解析】【分析】圆周角定理：同弧或等弧所对的圆周角相等，均等于所对圆心角的一半。

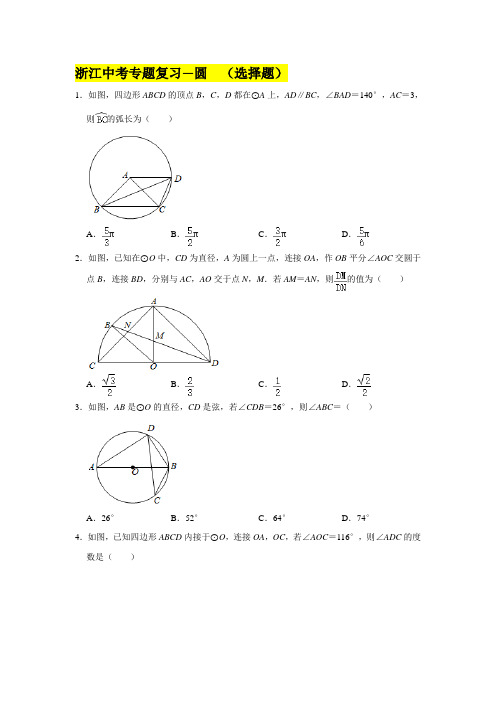
浙江中考专题复习—圆（选择题）1．如图，四边形ABCD的顶点B，C，D都在⊙A上，AD∥BC，∠BAD＝140°，AC＝3，则的弧长为（）A．πB．πC．πD．π2．如图，已知在⊙O中，CD为直径，A为圆上一点，连接OA，作OB平分∠AOC交圆于点B，连接BD，分别与AC，AO交于点N，M．若AM＝AN，则的值为（）A．B．C．D．3．如图，AB是⊙O的直径，CD是弦，若∠CDB＝26°，则∠ABC＝（）A．26°B．52°C．64°D．74°4．如图，已知四边形ABCD内接于⊙O，连接OA，OC，若∠AOC＝116°，则∠ADC的度数是（）A．122°B．120°C．117°D．116°5．已知，如图，线段AB是⊙O的直径，弦CD⊥AB于点E．若AE＝2，CD＝6，则OB的长度为（）A．B．C．D．56．如图，AB是⊙O的直径，点C为⊙O外一点，CA，CD分别与⊙O相切于点A，点D，连接BD，AD．若∠ACD＝50°，则∠DBA的度数是（）A．15°B．35°C．65°D．75°7．如图，⊙O的半径为5，点P在⊙O上，点A在⊙O内，且AP＝3，过点A作AP的垂线交⊙O于点B、C．设PB＝x，PC＝y，则y与x的函数表达式（）A．y＝B．y＝C．y＝2x D．y＝3x8．如图，⊙O的半径为2，弦AB平移得到CD（AB与CD位于点O两侧），且CD与⊙O相切于点E．若的度数为120°，则AD的长为（）A．4B．2C．D．39．如图，BC与⊙O相切于点B，CO连接并延长后交⊙O于点A，连接AB，若∠BAC＝36°，则∠C的度数为（）A．36°B．24°C．18°D．15°10．如图，⊙O的半径OD⊥AB于点C，连接AO并延长交⊙O于点E，连接EC．若AB＝8，CD＝2，则cos∠OCE为（）A．B．C．D．11.如图，在△ABC中，∠ACB＝90°，∠A＝40°，以C为圆心，CB为半径的圆交AB于点D，连接CD，则∠ACD＝（）A．10°B．15°C．20°D．25°12.如图，AD是半圆的直径，点C是弧BD的中点，∠ADC＝55°，则∠BAD等于（）A ．50°B ．55°C ．65°D ．70°13.圆内接正三角形、正方形、正六边形的边长之比为（ ）A.321：：B.321：：C.3123：：D.无法确定 14.如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm 2，则该半圆的半径为（ ）A.()54+cm B ．9cm C ．54cm D ．26cm15.如图，四边形ABCD 内接于O ，AE CB ⊥交CB 的延长线于点E ，若BA 平分DBE ∠，5AD =，13CE =，则(AE = )A ．3B ．32C ．43D ．2316.已知O 的半径为10cm ，弦//MN EF ，且12MN cm =，16EF cm =，则弦MN 和EF 之间的距离为( )cm ．A ．14或2B ．14C ．2D ．617.如图，扇形AOB 中，OA ＝2，C 为上的一点，连接AC ，BC ，如果四边形 AOBC 为菱形，则图中阴影部分的面积为（ ）A ．﹣B ．﹣2C ．﹣D ．﹣218.如图，一个半径为1的⊙O1经过一个半径为2的⊙O的圆心，则图中阴影部分的面积为( )A．1 B.12 C. 2 D.2219.如图，在边长为2的正方形ABCD中，点E是边CD的中点，以A为圆心，AB为半径作弧，交BE于点F．记图中分割部分的面积为S1，S2，则S1﹣S2的值为（）A．4﹣πB．2π﹣4 C．6﹣2πD．π﹣320.如图，在半径为的⊙O中，弦AB与CD交于点E，∠DEB＝75°，AB＝6，AE＝1，则CD的长是（）A．2B．2C．2D．421．如图，A、B、C三点在⊙O上，若∠ACB＝∠AOB，则∠AOB的度数是（）A．60°B．90°C．100°D．120°22．若四边形ABCD是圆内接四边形，则它的内角∠A，∠B，∠C，∠D的度数之比可能是（）A．3：1：2：5 B．1：2：2：3 C．2：7：3：6 D．1：2：4：3 23．如图，弦CD与直径AB相交，连接BC、BD，若∠ABC＝50°，则∠BDC＝（）A．20°B．30°C．40°D．50°24．下列各说法中：①圆的每一条直径都是它的对称轴；②长度相等的两条弧是等弧；③相等的弦所对的弧也相等；④同弧所对的圆周角相等；⑤90°的圆周角所对的弦是直径；⑥任何一个三角形都有唯一的外接圆；其中正确的有（）A．3个B．4个C．5个D．6个25．如图，半圆O的直径AB为15，弦BC为9，弦BD平分∠ABC，则BD的长是（）A．12 B．5C．6D．26．已知，点A、B是CD为直径的⊙O上两点，分别在直径的两侧．其中点A是弧的中点，若tan∠ACB＝2，则sin∠BCD的值为（）A．B．C．D．27．如图，AB是⊙O的直径，C为⊙O上的点，把△AOC沿OC对折，点A的对应点D恰好落在⊙O上，且C、D均在直径AB上方，连接AD、BD，若AC＝4，BD＝4，则AD的长度应是（）A．12 B．10 C．8D．628．如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF＝EB，EF与AB交于点C，连接OF，若∠AOF＝40°，则∠OFE的度数是（）A．30°B．20°C．40°D．35°29．如图，已知△ABC，O为AC上一点，以OB为半径的圆经过点A，且与BC、OC交于点E、D，设∠C＝α，∠A＝β，则（）A．若α+β＝70°，则弧DE的度数为20°B．若α+β＝70°，则弧DE的度数为40°C．若α﹣β＝70°，则弧DE的度数为20°D．若α﹣β＝70°，则弧DE的度数为40°30．如图，锐角三角形ABC内接于⊙O，连接AO并延长，交BC于点D，OE⊥BC于点E．设∠B＝α，∠C＝β，∠DOE＝γ，α＜β，则α，β，γ的关系正确的是（）A．β+γ＝2αB．α+β﹣γ＝90°C．α+β+γ＝180°D．α+γ＝β。

浙江中考知识点复习圆（解答题）1如图，将矩形ABCD绕点A按逆时针方向旋转，得到矩形AEFG，E点正好落在边CD上，连接BE，BG，且BG交AE于P．（1）求证：∠CBE＝∠BAE；（2）求证：BG＝2PB；（3）若AB＝，BC＝3，直接写出BG的长．2.已知⊙O的圆心为点O，半径为3，点M为⊙O内的一个定点，OM=5，AB、CD是圆O的两条相互垂直的弦，垂足为M．（1）当AB=4时，求四边形ADBC的面积；（2）当AB变化时，求四边形ADBC的面积的最大值.3.如图，A、P、B、C是⊙O上四点，∠APC＝∠CPB＝60°．（1）判断△ABC的形状并证明你的结论；（2）当点P位于什么位置时，四边形PBOA是菱形？并说明理由．（3）求证：PA+PB＝PC．4.如图，在扇形AOB 中，圆心角∠AOB ＝150°，D ，C 是AB ︵上的两点，∠DAB＝30°，C 是DB ︵的中点．(1)连结OD ，求证：△AOD 是等腰直角三角形；(2)若扇形的半径为2.①求AB 的长度；②求四边形ABCD 的面积．5.如图，AB 为⊙O 的直径，弦CD ⊥AB 于E ，∠CDB ＝15°，OE ＝2． （1）求⊙O 的半径；（2）将△OBD 绕O 点旋转，使弦BD 的一个端点与弦AC 的一个端点重合，则弦BD 与弦AC 的夹角为 ．6.如图，∠AOB ＝120°，OC 平分∠AOB ，∠MCN ＝60°，CM 与射线OA 相交于M 点，CN 与直线BO 相交于N 点．把∠MCN 绕着点C 旋转．（1）如图1，当点N 在射线OB 上时，求证：OC ＝OM +ON ；（2）如图2，当点N 在射线OB 的反向延长线上时，OC 与OM ，ON 之间的数量关系是 （直接写出结论，不必证明）7.如图，已知MN是⊙O的直径，AB是⊙O的弦，AB⊥MN，点C在线段AB上，OC＝AC＝2，BC＝4，求⊙O的半径．8．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，延长CA交⊙O于点E．连接ED交AB于点F．（1）求证：△CDE是等腰三角形．（2）当CD：AC＝2：时，求的值．9．已知四边形ABCD内接于⊙O，∠DAB＝90°．（Ⅰ）如图1，连接BD，若⊙O的半径为6，，求AB的长；（Ⅱ）如图2，连接AC，若AD＝5，AB＝3，对角线AC平分∠DAB，求AC的长．10．如图，AB是⊙O的直径，C是的中点，CE⊥AB于点E，BD交CE于点F．（1）求证：CF＝BF；（2）若CD＝6，AC＝8，求⊙O的半径及CE的长．11．如图，AB是⊙O的直径，点C和点D分别在AB和⊙O上，且AC＝AD，DC的延长线交⊙O于点E，过E作AC的平行线交⊙O于点F，连接AF，DF．（1）求证：四边形ACEF是平行四边形；（2）当sin∠EDF＝，BC＝4时，求⊙O的半径．12．如图，已知AC，BD为⊙O的两条直径，连接AB，BC，OE⊥AB于点E，点F是半径OC 的中点，连接EF．（1）设⊙O的半径为1，若∠BAC＝30°，求线段EF的长．（2）连接BF，DF，设OB与EF交于点P，①求证：PE＝PF．②若DF＝EF，求∠BAC的度数．13.如图，在△ABC中，AB＝AC，以AC为直径的⊙O交AB于点D，交BC于点E，DE与OB交于点F．（1）求证：BE＝CE．（2）若∠A＝45°，求的值．14.如图，在△ABC中，AC＝4，BC＝20，∠C＝90°，点O为AB边上一点，⊙O切边AC于点D，设CD＝x，⊙O的半径为y．（1）求y关于x的函数解析式；（2）当y＝5时，求⊙O在BC边上截得的线段EF的长．15.如图，Rt△ABC中，∠ABC＝90°，以BC为直径作⊙O交AC于点H，E为AC上一点，且AB＝AE，BE交⊙O于点D，OD交AC于点F．（1）求证：DO⊥AC．（2）若CE＝4，BC＝8，求DE的长．16.如图，AB是⊙O的直径，点C为圆上一点，点D为的中点，连接AD，作DE⊥AB交BC的延长线于点E．（1）求证：DE＝EB．（2）连接DO并延长交BC于点F．若CF＝2CE，BD＝5，求⊙O的半径．17.如图，AB是⊙O的直径，弦CD⊥AB于点E，G是弧AC上任意一点，连接AD，GD，AG．（1）找出图中和∠ADC相等的角，并给出证明；（2）已知BE＝2，AE＝8，求CD的长．18.如图，在Rt△ACB中，∠ACB＝90°，点D为BC延长线上一点，以BD为直径作半圆O分别交AB，AC于点G，E，点E为的中点，过点E作⊙O的切线交AB于点F．（1）求证：∠AEF＝∠ABC．（2）若sin A＝，FG＝1，求AC的长．19.如图，在△ABC中，BA＝BC，∠ABC＝90°，以AB为直径的半圆O交AC于点D，点E是弧BD上不与B、D重合的任意一点，连接AE交BD于点F，连接BE并延长交AC 于点G．（1）求证：△ADF≌△BDG．（2）若AB＝4，且点E是弧BD的中点，求阴影部分面积．（结果保留π）20.如图所示，⊙O的直径AB＝10cm，弦AC＝6cm，∠ACB的平分线交⊙O于点D，（1）求证：△ABD是等腰三角形；（2）求CD的长．。

第六单元圆第26课圆的基本性质考点一圆的有关概念1．在同一平面内，线段OP绕它固定的一个端点O旋转一周，另一个端点P所经过的封闭曲线叫做圆，定点O叫做______，线段OP叫做______．2．连结圆上任意两点的线段叫做________；经过圆心的弦叫做________；圆上任意两点间的部分叫做________；大于半圆的弧叫做________；小于半圆的弧叫做________；能完全重合的两条弧叫做________；圆的任意一条直径的两个端点分圆成两条弧，每一条弧都叫做________．考点二点和圆的位置关系3．如果圆的半径是r，点到圆心的距离为d，那么：点在圆外⇔________；点在圆上⇔________；点在圆内⇔________．考点三确定圆的条件4．________三个点确定一个圆，这个圆叫做以这三个点为顶点的三角形的________圆，这个三角形叫做这个圆的________三角形．5．三角形外接圆的圆心叫做三角形的________，是三角形两边________的交点，锐角三角形的外心在三角形的________，直角三角形的外心在三角形的________，钝角三角形的外心在三角形的________．考点四圆的对称性6．圆既是一个轴对称图形，又是一个________对称图形，圆还具有旋转不变性．7．圆有________条对称轴，经过________的直线都是它的对称轴．考点五垂径定理及其推论8．垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的________．9．推论：(1)________________的直径垂直于弦，并且平分弦所对的两条弧；(2)________的直径垂直平分弧所对的弦．考点六圆心角、弧、弦、弦心距之间的关系10．圆心角定理：在同圆或等圆中，相等的圆心角所对的弧________，所对的弦________．11．推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等，那么它们所对应的其余各对量都________．考点七圆心角与圆周角12．圆心角的度数等于它所对________的度数．13．圆周角的度数等于它所对的弧上圆心角度数的________．14．推论：半圆(或直径)所对的圆周角是____角；90°的圆周角所对的弦是________；在同圆或等圆中，同弧或等弧所对的圆周角________；相等的圆周角所对的弧________．15．在同圆或等圆中，一条弦所对的两个圆周角的大小关系是________．考点八圆内接四边形16．如果一个四边形的各个顶点在同一个圆上，那么这个四边形叫做________，这个圆叫做四边形的________．17．圆内接四边形的对角________，外角等于________．1．以下命题：①直径是弦；②三点确定一个圆；③同圆中等弧对等弦；④平分弦的直径必垂直于这条弦．其中正确的命题个数是(B)A．1B．2C．3D．42．如图26－1，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，CP，CM分别是AB上的高线和中线，如果⊙A的半径为2，那么下列判断正确的是( C )(图26－1)A．点P，M均在⊙A内B．点P，M均在⊙A外C．点P在⊙A内，点M在⊙A外D．点P在⊙A外，点M在⊙A内3．(2020 杭州)如图26－2，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上(不与点A，点C重合)，BD与OA交于点E.设∠AED＝α，∠AOD＝β，则(D)(图26－2)A. 3α＋β＝180°B. 2α＋β＝180°C. 3α－β＝90°D. 2α－β＝90°4．(2018 衢州)如图26－3，AC是⊙O的直径，弦BD⊥AO于点E，连结BC，过点O作OF⊥BC于点F，若BD＝8，AE＝2，则OF的长度是(D)(图26－3)A．3 B. 6 C．2.5 D. 5 5．(2019 台州)如图26－4，AC是圆内接四边形ABCD的一条对角线，点D关于AC的对称点E在BC上，连结AE.若∠ABC＝64°，则∠BAE的度数为__52°__．(图26－4)◆达标一 确定圆的条件例1 如图26－5，将△ABC 放在每个小正方形的边长为1的网格中，点A ，B ，C 均落在格点上，用一个圆面去覆盖△ABC ，能够完全覆盖这个三角形的最小圆面的半径是__5__．(图26－5) (图26－6) 变式1 (2020 青岛)如图26－6，已知△ABC ，求作：⊙O ，使其经过点B 和点C ，并且圆心O 在∠A 的平分线上．解：作∠CAB 角平分线和OB 的中垂线，交点即为圆心．◆达标二 垂径定理及其推论例2 如图26－7，⊙O 的直径AB ＝10，C 是AB 上一点，矩形ACND 交⊙O 于点M ，点N 在⊙O 上，若DN ＝8，则AD 的长为__4__．(图26－7)变式2 (2019 德州)如图26－8，CD 为⊙O 的直径，弦AB ⊥CD ，垂足为E ，AB︵＝BF ︵，CE ＝1，AB ＝6，则弦AF 的长度为__485__．(图26－8)【解析】 如图D26－1，连结OB 和OA ，OB 与AF 相交于点G .(图D26－1)∵弦AB ⊥CD ，AB ＝6，∴AE ＝BE ＝3，设半径为r ，则OE ＝r －1，在Rt △AEO 中，∵AO 2＝OE 2＋AE 2，∴r 2＝(r －1)2＋32，解得r ＝5.∵AB ︵＝BF ︵，∴OB ⊥AF ，∴AG ＝FG .∵12AG ·OB ＝12OE ·AB ，∴AG ＝245，则AF ＝485.◆达标三 圆心角、弧、弦、弦心距之间的关系例3 (2018 襄阳)如图26－9，点A ，B ，C ，D 都在半径为2的⊙O 上，若OA ⊥BC ，∠CDA ＝30°，则弦BC 的长为( D )(图26－9)A ．4B ．2 2 C. 3D ．2 3变式3 (2019 南京)如图26－10，⊙O 的弦AB ，CD 的延长线相交于点P ，且AB ＝CD ，求证：P A ＝PC .(图26－10)解：过O 作AB 和CD 的垂线，弦相等可得弦心距相等，从而可得结论． ◆达标四 圆周角定理及其推论例4 (2019 随州)如图26－11，点A ，B ，C 在⊙O 上，点C 在优弧AMB ︵上，若∠OBA ＝50°，则∠C 的度数为__40°__．(图26－11)变式4 (2020 黄石)如图26－12，点A ，B ，C 在⊙O 上，CD ⊥OA ，CE ⊥OB ，垂足分别为D ，E ，若∠DCE ＝40°，则∠ACB 的度数为( C )(图26－12)A ．140°B ．70°C ．110°D ．80° ◆达标四 圆的综合问题例5 (2019 河南)如图26－13，在△ABC 中，BA ＝BC ，∠ABC ＝90°.以AB 为直径的半圆O 交AC 于点D ，点E 是BD ︵上不与点B ，D 重合的任意一点，连结AE交BD 于点F ，连结BE 并延长交AC 于点G .(图26－13)(1)求证：△ADF ≌△BDG ；解：略(2)填空：①若AB ＝4，且点E 是BD ︵的中点，则DF 的长为__4－22__；②取AE︵的中点H ，当∠EAB 的度数为__30°__时，四边形OBEH 为菱形．变式5 (2019 福建)如图26－14，四边形ABCD 内接于⊙O ，AB ＝AC ，AC ⊥BD ，垂足为E ，点F 在BD 的延长线上，且DF ＝DC ，连结AF ，CF .(图26－14)(1)求证：∠BAC ＝2∠CAD ；(2)若AF ＝10，BC ＝45，求tan ∠BAD 的值．解：(1)设∠CAD ＝α＝∠CBD ，∴∠ACB ＝90－α.∵AC ＝AB ，∴∠BAC ＝2α＝2∠CAD ；(2)∵DF ＝DC ，∴∠DFC ＝∠DCF ，∴∠BDC ＝2∠DFC ，∴∠BFC ＝12∠BDC ＝12∠BAC ＝∠FBC ，∴CB ＝CF ，又BD ⊥AC ，∴AC 是线段BF 的中垂线，AB ＝AF ＝10＝AC .又BC ＝45，设AE ＝x ，则CE ＝10－x ，由AB 2－AE 2＝BC 2－CE 2，得100－x 2＝80－(10－x )2，解得x ＝6，∴AE ＝6，BE ＝8，CE ＝4，∴DE ＝AE ·CE BE ＝6×48＝3，∴BD ＝BE ＋DE ＝3＋8＝11，如图D26－2，作DH ⊥AB ，垂足为H ，(图D26－2)∵12AB ·DH ＝12BD ·AE ，∴DH ＝BD ·AE AB ＝11×610＝335，∴BH ＝BD 2－DH 2＝445，∴AH ＝AB －BH ＝10－445＝65，∴tan ∠BAD ＝DH AH ＝336＝112.1．(2020 湖州)如图26－15，已知AB 是半圆O 的直径，弦CD ∥AB ，CD ＝8，AB ＝10，则CD 与AB 之间的距离是__3__．(图26－15)2．如图26－16，△ABD 的三个顶点在⊙O 上，AB 是直径，点C 在⊙O 上，且∠ABD ＝52°，则∠BCD ＝__38°__．(图26－16)3．(2019 镇江)如图26－17，四边形ABCD 是半圆的内接四边形，AB 是直径，且AD ︵＝DC ︵.若∠C ＝110°，则∠ABC 的度数是__40°__．(图26－17)4．(2019 嘉兴)如图26－18，在⊙O 中，若弦AB ＝1，点C 在AB 上移动，连结OC ，过点C 作CD ⊥OC 交⊙O 于点D ，则CD 的最大值为__12__．(图26－18)5．(2018 温州)如图26－19，D 是△ABC 的边BC 上一点，连结AD ，作△ABD的外接圆，将△ADC 沿直线AD 折叠，点C 的对应点E 落在BD ︵上．(图26－19)(1)求证：AE ＝AB ；(2)若∠CAB ＝90°，cos ∠ADB ＝13，BE ＝2，求BC 的长．解：(1)∵△ADC 沿直线AD 折叠，点C 的对应点E 落在BF ︵上，∴∠ADE ＝∠ADC .∵四边形ADEB 是圆内接四边形，∴∠ADE ＋∠ABE ＝180°.∵∠ADC ＋∠ADB ＝180°.∴∠ABE ＝∠ADB .∵∠ADB 和∠AEB 为AB ︵所对圆周角，∴∠ADB ＝∠AEB ，∴AE ＝AB ；(2)如图D26－3，过点A 作AH ⊥BE 于点H .(图D26－3)∵AB ＝AE ，BE ＝2，∴BH ＝EH ＝1.∵∠ABE ＝∠AEB ＝∠ADB ，cos ∠ADB ＝13，∴cos ∠ABE ＝cos ∠ADB ＝13，∴BH AB ＝13，∴AC ＝AB ＝3.∵∠BAC ＝90°，∴BC ＝3 2.1．已知⊙O 的半径是5，点A 到圆心O 的距离是7，则点A 与⊙O 的位置关系是( C )A ．点A 在⊙O 上B ．点A 在⊙O 内C ．点A 在⊙O 外D ．无法判断2．如图Z26－1，点A ，B ，C 均在⊙O 上，当∠OBC ＝40°时，∠A 的度数是( A )(图Z26－1)A. 50°B. 55°C. 60°D. 65°3．如图Z26－2，BC 是半圆O 的直径，D ，E 是BC ︵上两点，连结BD ，CE 并延长交于点A ，连结OD ，OE .如果∠A ＝70°，那么∠DOE 的度数为( C )(图Z26－2)A. 35°B. 38°C. 40°D. 42°4．如图Z26－3，AB 是⊙O 的直径，C ，D 是⊙O 上的两点，∠AOC ＝120°，则∠CDB ＝__30°__．(图Z26－3)5．在半径为5的圆O 中，弦AB 的长为53，则弦AB 所对的圆周角的度数为__60°或120°__．6．如图Z26－4，一条公路的转弯处是一段圆弧(AB ︵)，点O 是这段弧所在圆的圆心，AB ＝40米，点C 是AB ︵的中点，点D 是AB 的中点，且CD ＝10米，则这段弯路所在圆的半径为__25米__．(图Z26－4)7．如图Z26－5，点A ，B ，C ，D ，E 在⊙O 上，且AB ︵的度数为50°，则∠E ＋∠C ＝__155__°.(图Z26－5)8．已知P 到圆O 上一点最长距离为10，最短距离为8，则圆O 的半径为__9或1__．9．如图Z26－6，由等边三角形、正方形、圆组成的轴对称图案中，等边三角形的周长与三个正方形的周长和的比值为__64__．(图Z26－6)10．如图Z26－7，已知四边形ABCD 内接于⊙O ，连结BD ，∠BAD ＝105°，∠BDC ＝30°.(图Z26－7)(1)求证：BD ＝CD ；(2)若⊙O 的半径为2，求△BDC 的面积． 解：(1)略；(2)作BH ⊥CD 于点H ，设BH ＝x ， 在Rt △BHC 中，x 2＋[(2－3)x ]2＝22，x 2＝2＋3， 所以S △BDC ＝12x ·2x ＝2＋ 3.11．如图Z26－8，四边形ABCD 是菱形，⊙O 经过点A ，C ，D ，与BC 相交于点E ，连结AC ，AE .若∠D ＝80°，则∠EAC 的度数为( D )(图Z26－8)A. 15°B. 20°C. 25°D. 30°12．如图Z26－9，已知⊙O 的半径为5，P 为圆O 外一点，PB ，PD 与圆O 分别交于点A ，B 和点C ，D 四点，且PO 平分∠BPD .当P A ＝1，∠BPO ＝45°时，则弦AB 的长为__6__．(图Z26－9)【解析】 作OH ⊥AB 于点H ，在△OBH 中，BH 2＋(BH ＋1)2＝52，解得BH ＝3，所以AB ＝6.13．如图Z26－10，AB 是⊙O 的直径，点C 为BD ︵的中点，CF 为⊙O 的弦，且CF ⊥AB ，垂足为E ，连结BD 交CF 于点G ，连结CD ，AD ，BF .(图Z26－10)(1)求证：△BFG ≌△CDG ； (2)若AD ＝BE ＝2，求BF 的长． 解：(1)略；(2)如图ZD26－1，连结OF ，设半径为r ，在Rt △ADB 中，BD 2＝(2r )2－4.(图ZD26－1)在Rt △OEF 中， EF 2＝r 2－(r －2)2. ∵CD ︵＝BC ︵＝BF ︵，∴BD ＝CF ，∴BD 2＝4EF 2， 代入可得(2r )2－4＝4[r 2－(r －2)2]， 解得r ＝1(舍)或3，则BF ＝2 3.14．如图Z26－11①是小明制作的一幅弓箭，点A ，D 分别是弓臂BAC 与弓弦BC 的中点，弓弦BC ＝60 cm ，沿AD 方向拉动弓弦的过程中，假设弓臂BAC 始终保持圆弧形，弓弦不伸长．如图②，当弓箭从自然状态的点D 拉到点D 1时，有AD 1＝30 cm ，∠B 1D 1C 1＝120°.① ② ③(图Z26－11)(1)图②中，弓臂两端B 1，C 1的距离为__303__cm ；(2)如图③，将弓箭继续拉到点D 2，使弓臂B 2AC 2为半圆，则D 1D 2的长为__(105－10)__cm.解：(1)如图ZD26－2①中，连结B 1C 1交DD 1于点H . ∵D 1A ＝D 1B 1＝30，∴D 1是B 1AC 1︵的圆心． ∵AD 1⊥B 1C 1，∴B 1H ＝C 1H ＝153， ∴B 1C 1＝303，∴弓臂两端B 1，C 1的距离为30 3 cm ；①②(图ZD26－2)(2)如图ZD26－2②中，连结B 1C 1交DD 1于点H ，连结B 2C 2交DD 2于点G . 设半圆的半径为r ，则πr ＝120π×30180，∴r ＝20， ∴AG ＝GB 2＝20，GD 1＝30－20＝10， 在Rt △GB 2D 2中，GD 2＝302－202＝105， ∴D 1D 2＝(105－10)cm.。

浙江中考复习----圆（填空题）1．如图是一个圆环形黄花梨木摆件的残片，为求其外圆半径，小林在外圆上任取一点A，然后过点A作AB与残片的内圆相切于点D，作CD⊥AB交外圆于点C，测得CD＝15cm，AB＝60cm，则这个摆件的外圆半径是cm．2.如图所示，已知C为的中点，OA⊥CD于M，CN⊥OB于N，若OA＝r，ON＝a，则CD＝．3.如图，MN为⊙O的直径，MN＝10，AB为⊙O的弦，已知MN⊥AB于点P，AB＝8，现要作⊙O的另一条弦CD，使得CD＝6且CD∥AB，则PC的长度为．4.如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，BC∥QR，则∠AOQ=________.5.如图，在Rt△ABC中，∠ABC＝90°，AB＝2，BC＝2，以AB的中点为圆心，OA的长为半径作半圆交AC于点D，则图中阴影部分的面积为（计算结果保留π）6.如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B，O分别落在点B1，C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（，0），B（0，4），则点B2018的坐标为．7.如图，已知点E为圆外的一点，EA交圆于点B，EC交圆于点D，若＝80°，＝30°，则∠BED＝度．8.如图，点A、B、C是半径为4的⊙O上的三个点，若∠BAC＝45°，则弦BC的长等于．9.如图，已知AB是半圆O的直径，弦CD∥AB，CD＝8，AB＝10，则CD与AB之间的距离是．10.如图，四边形ABCD内接于⊙O，连接AC，若AC＝AD，且∠DAC＝50°，则∠B的度数为．11.如图，在⊙O中，弦AB＝1，点C在AB上移动，连接OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为．12.如图，点A，B，C都在⨀O上，tan∠ABC＝，将圆O沿BC翻折后恰好经过弦AB的中点D，则的值是．13.如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，D为弧AC的中点，E为BA延长线上一点，若∠DAE＝108°，则∠CAD＝度．14.如图，在△ABC中，BA，BC分别为⊙O的切线，点E和点C为切线点，线段AC经过圆心O且与⊙O相交于D、C两点，若tan A＝，AD＝2，则BO的长为．15.如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AC＝2，以C为圆心，r为半径作圆．若该圆与线段AB只有一个交点，则r的取值范围为．16.如图将母线长为9的圆锥侧面展开后得到扇形的圆心角为120°，若将该扇形剪成两个同样的扇形再围成2个同样的圆锥，则新圆锥的底面半径是．17.如图，点A，点B，点C在⊙O上，分别连接AB，BC，OC．若AB＝BC，∠B＝40°，则∠OCB＝．18.如图，矩形ABCD中，AB＝7cm，BC＝6cm，⊙O与矩形的边AB、BC、CD分别相切于点E、F、G，点P是⊙O上任意一点，则线段AP长度的最小值为．19.已知王星记的一款折扇打开后是一个圆心角为120的扇形，半径为30厘米，则打开后折扇的弧长是．20.如图，曲线AMNB和MON是两个半圆，MN∥AB，大半圆半径为2，则阴影部分的面积是．21.如图，直线AB与⊙O相切于点C，AO交⊙O于点D，连接CD，OC．若∠AOC＝60°，则∠ACD＝°．22.如图，已知AD是∠BAC的平分线，以线段AB为直径作圆，交∠BAC和角平分线于C，D两点．过D向AC作垂线DE垂足为点E．若DE＝2CE＝4，则直径AB＝．23.如图，P A，PB分别切⊙O于A，B两点，CD切⊙O于点E．若P A＝10，则△PCD的周长为．24.如图1，是某隧道的入口，它的截面如图2所示，是由和Rt∠ACB围成，且点C也在所在的圆上，已知AC＝4m，隧道的最高点P离路面BC的距离DP＝7m，则该道路的路面宽BC＝m；在上，离地面相同高度的两点E，F装有两排照明灯，若E是的中点，则这两排照明灯离地面的高度是m．25.如图，在圆心角为90°的扇形ACB中，半径CA＝6，以AC为直径作半圆O．过点O作BC的平行线交两弧于点D、E，则图中阴影部分的面积是．26.在平面直角坐标系中，点O为坐标原点，A、B、C三点的坐标为（，0）、（3，0）、（0，5），点D在第一象限，且∠ADB＝60°，则线段CD的长的最小值为．。