3.1.1方程的根与函数的零点学案

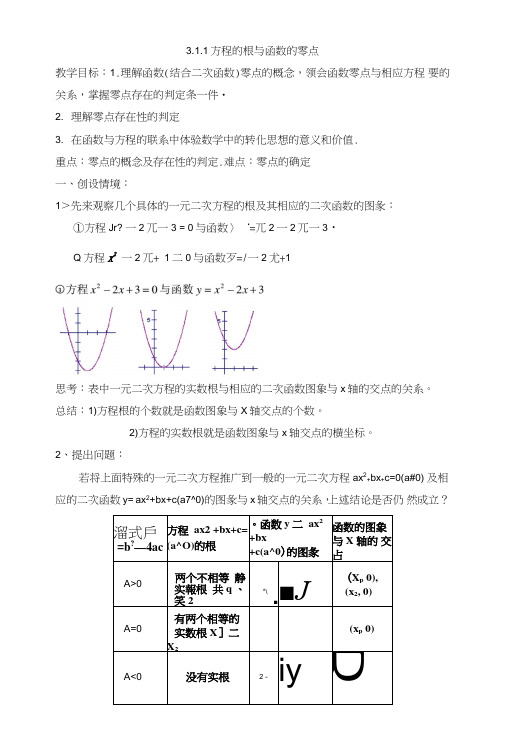
3.1.1方程的根与函数的零点教学目标：1.理解函数(结合二次函数)零点的概念，领会函数零点与相应方程要的关系，掌握零点存在的判定条一件・2. 理解零点存在性的判定3. 在函数与方程的联系中体验数学中的转化思想的意义和价值.重点：零点的概念及存在性的判定.难点：零点的确定一、创设情境：1＞先来观察几个具体的一元二次方程的根及其相应的二次函数的图彖：①方程Jr? 一2兀一3 = 0与函数〉‘=兀2一2兀一3・Q方程x2一2兀+ 1二0与函数歹=/一2尤+1思考：表中一元二次方程的实数根与相应的二次函数图象与x轴的交点的关系。

总结：1)方程根的个数就是函数图象与X轴交点的个数。

2)方程的实数根就是函数图象与x轴交点的横坐标。

2、提出问题：若将上面特殊的一元二次方程推广到一般的一元二次方程ax2+bx+c=0(a#0) 及相应的二次函数y= ax2+bx+c(a7^0)的图彖与x轴交点的关系，上述结论是否仍然成立？溜式戶=b?—4ac 方程ax2 +bx+c=(a^O)的根。

函数y二ax2+bx+c(a^0)的图彖函数的图象与X轴的交占A>0两个不相等静实報根共q 、笑2x\■■J(X p 0),(x2, 0)A=0有两个相等的实数根X］二X2(x p 0)A<0没有实根 2 -iyB总结：可见上述关系对一般的一元二次ax2+bx+c=O(a^O)及相应的二次函数y= ax2+bx+c(a^O)也是成立的二、讲授新课：3、函数零点的概念：对于函数y = f(x)(xe D),把使/(x) = 0成立的实数兀叫做函数y 二/(X)(XG£>)的零点.函数零点的意义：函数y = /(%)的零点就是方程/(X)= 0实数根，亦即函数y = /(x)的图象与兀轴交点的横坐标.即：方程/(%) = 0有实数根o函数y = /(x)的图象与兀轴有交点o函数y = fM有零点.(1)求函数丁 = /(兀)零点的方法：①方程法：求方程fM = 0的实数根；®图像法：画出函数yh(x)的图象，其图象与x轴交点的横坐标是函数yh(x)的零点例1.求下列函数的零点：1 /(x) = x2-x-2 2 /(兀)二3兀一23 f(X)= e x 4. /W = lnx+2x-64、零点存在性的探索：（I ）观察二次函数f（x） = x2-2x-3的图象:®在区间［-2,1］±有零点_______ ;/（-2） = ______ ， /（D= _______/（-2）• /（D _____ 0 （＜或＞）・©在区间［2,4］上有零点______ ;/⑵• /⑷—0 （V或〉）.（II）观察下面函数y = /（x）的图象®在区间［恥］上 _____ （有/无）零点；/⑺）•0 （＜或＞）・©在区间|Z?,c］±_______ （有/无）零点；/的• /（c）_____ 0（＜或〉）・©在区间［c,〃］上____ （有/无）零点；/（C）• /（d）___ 0（V或〉）・由以上两步探索，你可以得出什么样的结论？（结合函数图象，思考、讨论、总结归纳得出函数零点存在的条件，并进行交流、评析）总结：函数零点存在性定理5、怎样利用函数零点存在性定理，断定函数在某给定区间上是否存在零点.三、例题讲解：例:1.求函数/（兀）=lnx + 2x-6的零点个数.问题：1) 你可以想到什么方法来判断函数零点个数？2) 判断函数的单调性，由单调性你能得该函数的单调性具有什么特性？(引导学生探索判断函数零点的方法，指出可以借助计算机或计算器来画函数的图象，结合图象对函数有一个零点形成直观的认识・)四、当堂训练：1. 利用函数图象判断下列方程有没有根，有几个根：(1) —兀~ + 3x + 5 = 0；(2) 2x(x — 2) = —3 ；(3) x2 = 4x —4；(4) 5X2+2X =3X2+5・2. 利用函数的图象，指出下列函数零点所在的大致区间:(1) / (x)=—无‘ 一3x + 5 ；(2) /(x) = 2xln(x-2)-3 ；(3) f(x) = e x~{(4) /(x) = 3(x+ 2)(x-3)(x + 4) + 兀五•、布置作业：教材P92 (A组)第1、2题；。

《3.1.1方程的根与函数的零点》导学案班级：高一（3）班指导老师：高一数学备课组成员授课人：时间：第1课时（总2课时）课型新授课课前准备学生课前预习、PPT与智慧课堂等课堂资源整合。

学习目标1．理解函数的零点与方程的根的联系.2．理解并会用零点存在定理判断函数的零点．3.体会从特殊到一般，数形结合思想,化归与转化思想以及函数与方程思想的意义和价值，培养学生自主发现、探究实践的能力．4.培养学生锲而不舍的探索精神和严密思考的良好学习习惯.教学重点、教学难点重点：理解函数的零点与方程的根之间的联系，掌握零点存在的判定条件．难点：探究发现函数零点的存在性.学情分析在本节课之前，学生对二次函数和一元二次方程已经比较熟悉，会判断具体的一元二次方程有没有根，有几个根，会用十字相乘法和求根公式求根. 但是对二次函数与一元二次方程的联系认识不全面，也没有上升到一般的函数与方程的层次.因此，在讲解本节内容时，让学生对函数与方程的关系及零点存在定理有较为全面的认识.导学过程教学过程学生活动教师指导信息技术融合情况目标提示1．一元二次方程的根与所对应的二次函数的图象的关系；2．函数的零点、方程的根及其所对应的函数图象三者之间的关系；3．函数零点存在性定理的理解和应用.回顾求一元二次方程的根的方法及二次函数的图象教师借助PPT课件强调本节学习目标．情景引入通过问题1引入一些复杂的方程无法求解，造成学生的认知冲突,引发学生的好奇心和求知欲。

教师借助PPT展示所要研究的问题．交流讨论探究1：一元二次方程的根与二次函数的图象之间的关系 方程 x 2-2x-3=0 x 2-2x+1=0 x 2-2x+3=0 函数方程的实数根函数图象与x 轴的交点指导学生画图并观察一元二次方程的根与二次函数图象的关系。

教师利用 PPT展示正确答案释疑解难1、函数零点的定义2、结论3、求函数零点的方法 小试牛刀探究2 函数零点存在性定理观察二次函数32)(2--=x x x f 的图象，可以发现① 在区间[-2,1]上有零点______。

课题：§3.1.1方程的根与函数的零点苍溪中学 姚智铭学习目标：（一）知识与技能：1．结合二次函数的图象，判断一元二次方程根的存在性及根的个数，从而了解函数的零点与方程的根的联系.2．理解并会用函数在某个区间上存在零点的判定方法． （二）过程与方法：自主发现、探究实践，体会函数的零点与方程的根之间的联系． （三）情感、态度、价值观：在函数与方程的联系中体验数学转化思想的意义和价值.重点难点：重点：体会函数的零点与方程的根之间的联系，掌握零点存在的判定条件． 难点：探究发现函数零点的存在性.问题·探究（一）回顾旧知，发现问题问题1 求下列方程的根．（1）023=+x ；（2）0652=+-x x ； （3）062ln =-+x x .问题2观察下表(一)，求出表中一元二次方程的实数根，画出相应的二次函数图象的简图，并写出函数图象与x 轴交点的坐标问题 3 若将上面特殊的一元二次方程推广到一般的一元二次方程20ax bx c ++=(0)a >及相应的二次函数c bx ax y ++=2(0)a >的图象与x 轴交点的关系，上述结论是否仍然成立？（二）总结归纳，形成概念1、函数的零点：辨析练习：函数223y x x =--的零点是：（ ）A ．（-1，0），（3，0）；B ．x=-1；C ．x=3；D ．-1和3． 2、等价关系：（三）初步运用，示例练习例1 求函数)1lg()(-=x x f 的零点．小结：求函数零点的步骤：变式练习： 求下列函数的零点（1）65)(2+-=x x x f ； （2）12)(-=x x f（四）分组讨论，探究结论（零点存在性）问题4：函数y ＝f(x)在某个区间上是否一定有零点？怎样的条件下，函数y ＝f(x)一定有零点？（1）观察二次函数32)(2--=x x x f 的图象：○1 在区间]1,2[-上有零点______；=-)2(f _______，=)1(f _______, )2(-f ·)1(f _____0（＜或＞）．○2 在区间]4,2[上有零点______；)2(f ·)4(f ____0（＜或＞）．（2）观察下面函数)(x f y =的图象○1 在区间],[b a 上______(有/无)零点；)(a f ·)(b f _____0（＜或＞）．○2 在区间],[c b 上______(有/无)零点；)(b f ·)(c f _____0（＜或＞）．○3 在区间],[d c 上______(有/无)零点；)(c f ·)(d f _____0（＜或＞）．（3）观察屏幕上的函数图象： 若函数在某区间内存在零点，则函数在该区间上的图象是 （间断／连续）；含零点的某一较小区间中以零点左右两边的实数为自变量，它们各自所对应的函数值的符号是 （相同／互异）由以上探索，你可以得出什么样的结论？讨论：（1）从这一结论中可看出，函数具备了哪些条件，就可断言它有零点存在呢？（2）如果函数具备上述两个条件时，函数有多少零点呢？（3）如果把结论中的条件“图象连续不断”除去不要，又会怎样呢？（4）如果把结论中的条件“f(a)f(b)＜0’’去掉呢？（5）若函数y=f(x) 在区间(a, b)内有零点，一定能得出f(a)·f(b)<0的结论吗？（6）在什么样的条件下，就可确定零点的个数呢，零点的个数是惟一的呢？小结：（五）观察感知，例题学习例2（教材第96页）求函数f(x)=㏑x + 2x – 6 的零点个数试一试：你能判断出方程㏑x = - x2 + 3 实数根的个数吗？（六）反思小结,提升能力1．函数零点的定义2．等价关系函数Y=f(x)函数Y=f(x)的图象与X轴交点的横坐标方程f(x)＝0实数根3．函数的零点或相应方程的根的存在性以及个数的判断。

3.1.1 方程的根与函数的零点一、教学目标：1.让学生熟练掌握二次函数的图象，并会判断一元二次方程根的存在性及根的个数2.让学生了解函数的零点与方程根的联系3.让学生认识到函数的图象及基本性质（特别是单调性）在确定函数零点中的作用4．培养学生动手操作的能力二、教学重点、难点重点 零点的概念及存在性的判定． 难点 零点的确定．三、学法与教学用具学法：学生在老师的引导下，通过阅读教材，自主学习、思考、交流、讨论和概括，从而完成本节课的教学目标。

教学用具：投影仪。

教学过程：(一)创设情景，揭示课题1、提出问题：一元二次方程 a x 2+bx+c=0 (a ≠0)的根与二次函数y=a x 2+bx+c(a ≠0)的图象有什么关系？2．先来观察几个具体的一元二次方程的根及其相应的二次函数的图象：（用投影仪给出）①方程0322=--x x 与函数322--=x x y②方程0122=+-x x 与函数122+-=x x y③方程0322=+-x x 与函数322+-=x x y1．师：引导学生解方程，画函数图象，分析方程的根与图象和x 轴交点坐标的关系． 要求学生：独立思考完成解答，观察、思考、总结、概括得出结论，并进行交流． 师：上述结论推广到一般的一元二次方程和二次函数又怎样？(二) 互动交流 研讨新知通过上述问题引出函数零点的概念：定义：对于函数()y f x =，我们把使()0f x =的实数x 叫做函数()y f x =的零点（zero point ）.指出函数零点的意义：函数)(x f y =的零点就是方程0)(=x f 实数根，亦即函数)(x f y =的图象与x 轴交点的横坐标．即：方程0)(=x f 有实数根⇔函数)(x f y =的图象与x 轴有交点⇔函数)(x f y =有零点．想一想，怎样求函数的零点呢？师：引导学生认真理解函数零点的意义，并根据函数零点的意义探索其求法：①代数法；求方程0)(=x f 的实数根；②几何法．将它与函数)(x f y =的图象联系起来，并利用函数的性质找出零点。

课题：§3.1.1方程的根与函数的零点
学习目标： 知识与技能 理解函数（结合二次函数）零点的概念，领会函数零点与相应方程要的关系，掌握零点存在的判定条件．
过程与方法 零点存在性的判定．
情感、态度、价值观 在函数与方程的联系中体验数学中的转化思想的意义和价值． 学习重点：
重点 零点的概念及存在性的判定． 难点 零点的确定． 学习程序与环节设计：
学习过程与操作设计：
结合二次函数引入课题．
二次函数的零点及零点存在性的．
研究二次函数在零点、零点之内及零点外的函数值符号，并尝试进行系统的总结．。

第三章 函数的应用 §3.1 函数与方程3.1.1 方程的根与函数的零点自主学习1．能够结合二次函数的图象判断一元二次方程根的存在性及根的个数． 2．理解函数的零点与方程根的关系． 3．掌握函数零点的存在性的判定方法．1．对于函数y ＝f (x )，我们把使f (x )＝0的实数x 叫做函数y ＝f (x )的________．2．函数y ＝f (x )的零点就是方程f (x )＝0的__________，也就是函数y ＝f (x )的图象与x 轴的交点的__________．3．方程f (x )＝0有实数根⇔函数y ＝f (x )的图象与x 轴有________⇔函数y ＝f (x )有________．4．函数零点的存在性的判定方法如果函数y ＝f (x )在[a ，b ]上的图象是连续不断的一条曲线，并且有f (a )·f (b )________0，那么y ＝f (x )在区间(a ，b )内有零点，即存在c ∈(a ，b )，使得f (c )________0，这个c 也就是方程f (x )＝0的根．对点讲练求函数的零点【例1】 求下列函数的零点：(1)f (x )＝－x 2－2x ＋3； (2)f (x )＝x 4－1； (3)f (x )＝x 3－4x .规律方法 求函数的零点，关键是准确求解方程的根，若是高次方程，要进行因式分解，分解成多个因式积的形式且方程的另一边为零，若是二次方程常用因式分解或求根公式求解．变式迁移1 若函数f (x )＝x 2＋ax ＋b 的零点是2和－4，求a ，b 的值．判断函数在某个区间内是否有零点【例2】 (1)函数f (x )＝ln x －2x的零点所在的大致区间是( )A ．(1,2)B ．(2,3) C.⎝⎛⎭⎫1，1e 和(3,4) D ．(e ，＋∞)(2)f (x )＝ln x －2x在x >0上共有________个零点．规律方法 这是一类非常基础且常见的问题，考查的是函数零点的判定方法，一般而言只需将区间端点代入函数求出函数值，进行符号判断即可得出结论，这类问题的难点往往是函数符号的判断，可运用函数的有关性质进行判断，同时也要注意该函数的单调性．变式迁移2 方程x 2－3x ＋1＝0在区间(2,3)内根的个数为( ) A ．0 B ．1 C ．2 D ．不确定已知函数零点的特征，求参数范围【例3】 若函数f (x )＝ax 2－x －1仅有一个零点，求实数a 的取值范围．变式迁移3 已知在函数f (x )＝mx 2－3x ＋1的图象上其零点至少有一个在原点右侧，求实数m 的范围．1．函数f (x )的零点就是方程f (x )＝0的根，但不能将它们完全等同．如函数f (x )＝x 2－4x ＋4只有一个零点，但方程f (x )＝0有两个相等实根．2．并不是所有的函数都有零点，即使在区间[a ，b ]上有f (a )·f (b )<0，也只说明函数y ＝f (x )在(a ，b )上至少有一个零点，但不一定唯一．反之，若f (a )·f (b )>0，也不能说明函数y ＝f (x )在区间(a ，b )上无零点，如二次函数y ＝x 2－3x ＋2在[0,3]上满足f (0)·f (3)>0，但函数f (x )在区间(0,3)上有零点1和2.3．函数的零点是实数而不是坐标轴上的点．课时作业一、选择题1．若函数f (x )唯一的零点在区间(1,3)，(1,4)，(1,5)内，那么下列说法中错误的是( ) A ．函数f (x )在(1,2)或[2,3)内有零点 B ．函数f (x )在(3,5)内无零点 C ．函数f (x )在(2,5)内有零点D ．函数f (x )在(2,4)内不一定有零点2．函数f (x )＝log 3x －8＋2x 的零点一定位于区间( ) A ．(5,6) B ．(3,4) C ．(2,3) D ．(1,2)3．函数f (x )＝ax 2＋bx ＋c ，若f (1)>0，f (2)<0，则f (x )在(1,2)上零点的个数为( )A．至多有一个B．有一个或两个C．有且仅有一个D．一个也没有4．已知f(x)是定义域为R的奇函数，且在(0，＋∞)内的零点有1 003个，则f(x)的零点的个数为()A．1 003 B．1 004 C．2 006 D．2 0075．若函数y＝f(x)在区间[0,4]上的图象是连续不断的曲线，且方程f(x)＝0在(0,4)内仅有一个实数根，则f(0)·f(4)的值()A．大于0 B．小于0 C．等于0 D．无法判断二、填空题6．二次函数f(x)＝ax2＋bx＋c中，a·c<0，则函数的零点有________个．7．若函数f(x)＝ax＋b(a≠0)有一个零点是2，那么函数g(x)＝bx2－ax的零点是__________．8．方程2ax2－x－1＝0在(0,1)内恰有一个实根，则实数a的取值范围是____________．三、解答题9．判断下列函数在给定区间上是否存在零点．(1)f(x)＝x2－3x－18，x∈[1,8]；(2)f(x)＝x3－x－1，x∈[－1,2]；(3)f(x)＝log2(x＋2)－x，x∈[1,3]．10．已知函数f(x)＝x2－(k－2)x＋k2＋3k＋5有两个零点．(1)若函数的两个零点是－1和－3，求k的值；(2)若函数的两个零点是α和β，求α2＋β2的取值范围．第三章函数的应用§3.1函数与方程3．1.1方程的根与函数的零点答案自学导引1．零点2．实数根横坐标3．交点零点4．< ＝ 对点讲练【例1】 解 (1)由于f (x )＝－x 2－2x ＋3＝－(x ＋3)(x －1)． 所以方程－x 2－2x ＋3＝0的两根是－3,1. 故函数的零点是－3,1. (2)由于f (x )＝x 4－1＝(x 2＋1)(x ＋1)(x －1)，所以方程x 4－1＝0的实数根是－1,1， 故函数的零点是－1,1.(3)令f (x )＝0，即x 3－4x ＝0，∴x (x 2－4)＝0，即x (x ＋2)(x －2)＝0. 解得：x 1＝0，x 2＝－2，x 3＝2，所以函数f (x )＝x 3－4x 有3个零点，分别是－2,0,2. 变式迁移1 解 ∵2，－4是函数f (x )的零点， ∴f (2)＝0，f (－4)＝0. 即⎩⎪⎨⎪⎧ 2a ＋b ＝－4－4a ＋b ＝－16，解得⎩⎪⎨⎪⎧a ＝2b ＝－8. 【例2】 (1)B (2)1解析 (1)∵f (1)＝－2<0， f (2)＝ln 2－1<0，∴在(1,2)内f (x )无零点，A 不对；又f (3)＝ln 3－23>0，∴f (2)·f (3)<0，∴f (x )在(2,3)内有一个零点．(2)f (x )＝ln x －2x在x >0上是增函数，且f (2)·f (3)<0，故f (x )有且只有一个零点．变式迁移2 B [令f (x )＝x 2－3x ＋1，∴其对称轴为x ＝32，∴f (x )在(2,3)内单调递增，又∵f (2)·f (3)<0， ∴方程在区间(2,3)内仅有一个根．]【例3】 解 ①若a ＝0，则f (x )＝－x －1，为一次函数，易知函数仅有一个零点； ②若a ≠0，则函数f (x )为二次函数，若其只有一个零点，则方程ax 2－x －1＝0仅有一个实数根，故判别式Δ＝1＋4a ＝0，则a ＝－14.综上，当a ＝0或a ＝－14时，函数仅有一个零点．变式迁移3 解 (1)当m ＝0时，f (0)＝－3x ＋1，直线与x 轴的交点为⎝⎛⎭⎫13，0，即函数的零点为13，在原点右侧，符合题意．图①(2)当m ≠0时，∵f (0)＝1， ∴抛物线过点(0,1)．若m <0，f (x )的开口向下，如图①所示．二次函数的两个零点必然是一个在原点右侧，一个在原点左侧．图②若m >0，f (x )的开口向上，如图②所示，要使函数的零点在原点右侧，当且仅当9－4m ≥0即可，解得0<m ≤94，综上所述，m 的取值范围为 ⎝⎛⎦⎤－∞，94. 课时作业 1．C2．B [f (3)＝log 33－8＋2×3＝－1<0， f (4)＝log 34－8＋2×4＝log 34>0. 又f (x )在(0，＋∞)上为增函数， 所以其零点一定位于区间(3,4)．]3．C [若a ＝0，则f (x )＝bx ＋c 是一次函数， 由f (1)·f (2)<0得零点只有一个；若a ≠0，则f (x )＝ax 2＋bx ＋c 为二次函数，如有两个零点，则必有f (1)·f (2)>0，与已知矛盾．故f (x )在(1,2)上有且仅有一个零点．]4．D [因为f (x )是奇函数，则f (0)＝0，又在(0，＋∞)内的零点有1 003个，所以f (x )在 (－∞，0)内的零点有1 003个．因此f (x )的零点共有1 003＋1 003＋1＝2 007个．] 5．D [考查下列各种图象上面各种函数y ＝f (x )在(0,4)内仅有一个零点， 但是(1)中，f (0)·f (4)>0， (2)中f (0)·f (4)<0，(3)中f (0)·f (4)＝0.] 6．2解析 ∵Δ＝b 2－4ac >0，∴方程ax 2＋bx ＋c ＝0有两个不等实根，即函数f (x )有2个零点．7．0，－12解析 由2a ＋b ＝0，得b ＝－2a ，g (x )＝bx 2－ax ＝－2ax 2－ax ，令g (x )＝0，得x ＝0或x ＝－12，∴g (x )＝bx 2－ax 的零点为0，－12.8．(1，＋∞)解析 令f (x )＝2ax 2－x －1，a ＝0时不符合题意；a ≠0且Δ＝0时，解得a ＝－18，此时方程为－14x 2－x －1＝0，也不合题意；只能f (0)·f (1)<0，解得a >1.9．解 (1)方法一 ∵f (1)＝－20<0，f (8)＝22>0， ∴f (1)·f (8)<0.故f (x )＝x 2－3x －18在[1,8]上存在零点．方法二 令x 2－3x －18＝0，解得x ＝－3或x ＝6， ∴函数f (x )＝x 2－3x －18在[1,8]上存在零点． (2)∵f (－1)＝－1<0，f (2)＝5>0， ∴f (－1)·f (2)<0.故f (x )＝x 3－x －1在[－1,2]上存在零点． (3)∵f (1)＝log 2(1＋2)－1>log 22－1＝0， f (3)＝log 2(3＋2)－3<log 28－3＝0， ∴f (1)·f (3)<0.故f (x )＝log 2(x ＋2)－x 在[1,3]上存在零点．10．解 (1)∵－1和－3是函数f (x )的两个零点，∴－1和－3是方程x 2－(k －2)x ＋k 2＋3k ＋5＝0的两个实数根． 则⎩⎪⎨⎪⎧－1－3＝k －2，－1×(－3)＝k 2＋3k ＋5， 解得k ＝－2.(2)若函数的两个零点为α和β，则α和β是方程x 2－(k －2)x ＋k 2＋3k ＋5＝0的两根，∴⎩⎪⎨⎪⎧α＋β＝k －2，αβ＝k 2＋3k ＋5，Δ＝(k －2)2－4×(k 2＋3k ＋5)≥0.则⎩⎪⎨⎪⎧α2＋β2＝(α＋β)2－2αβ＝－k 2－10k －6，－4≤k ≤－43， ∴α2＋β2在区间⎣⎡⎦⎤－4，－43上的最大值是18，最小值是509， 即α2＋β2的取值范围为⎣⎡⎦⎤509，18.。

3.1.1 方程的根与函数的零点教案【教学目标】1. 结合二次函数的图象，判断一元二次方程根的存在性及根的个数，从而了解函数的零点与方程根的联系；2. 掌握零点存在的判定条件. 【教学重难点】教学重点：方程的根与函数的零点的关系。

教学难点：求函数零点的个数问题。

【教学过程】(一)预习检查、总结疑惑检查落实了学生的预习情况并了解了学生的疑惑，使教学具有了针对性。

（二）情景导入、展示目标。

探究任务一：函数零点与方程的根的关系问题：① 方程2230x x --=的解为 ，函数223y x x =--的图象与x 轴有 个交点，坐标为 .② 方程2210x x -+=的解为 ，函数221y x x =-+的图象与x 轴有 个交点，坐标为 .③ 方程2230x x -+=的解为 ，函数223y x x =-+的图象与x 轴有 个交点，坐标为 .根据以上结论，可以得到：一元二次方程20(0)ax bx c a ++=≠的根就是相应二次函数20(0)y ax bx c a =++=≠的图象与x 轴交点的 .你能将结论进一步推广到()y f x =吗？已经布置学生们课前预习了这部分，检查学生预习情况并让学生把预习过程中的疑惑说出来。

新知：对于函数()y f x =，我们把使()0f x =的实数x 叫做函数()y f x =的零点（zero point ）.反思：函数()y f x =的零点、方程()0f x =的实数根、函数()y f x = 的图象与x 轴交点的横坐标，三者有什么关系？试试：（1）函数244y x x =-+的零点为 ； （2）函数243y x x =-+的零点为 .小结：方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有交点⇔函数()y f x =有零点.探究任务二：零点存在性定理问题：① 作出243y x x =-+的图象，求(2),(1),(0)f f f 的值，观察(2)f 和(0)f 的符② 观察下面函数()y f x =的图象，在区间[,]a b 上 零点；()()f a f b 0；在区间[,]b c 上 零点；()()f b f c 0；在区间[,]c d 上 零点；()()f c f d 0.新知：如果函数()y f x =在区间[,]a b 上的图象是连续不断的一条曲线，并且有()()f a f b <0，那么，函数()y f x =在区间(,)a b 内有零点，即存在(,)c a b ∈，使得()0f c =，这个c 也就是方程()0f x =的根.讨论：零点个数一定是一个吗？ 逆定理成立吗？试结合图形来分析.（三）典型例题例1求函数()ln 26f x x x =+-的零点的个数. 解析：引导学生借助计算机画函数图像，缩小解的范围。

必修一 §3.1.1方程的根与函数的零点(第1课时）教师：【学习目标】1.了解方程根与对应函数图象和x 轴的交点的关系。

2.理解函数零点的概念和等价关系。

3.掌握简单函数零点的求法。

【重点难点】重点：方程的根与函数的零点之间的关系。

难点：求函数的零点和等价关系之间的转换。

【学法指导】1.根据学习目标，准确地从教材中提取有效信息；2.根据预习案再次研读教材，自主探究导学案问题，将预习案中不能解决的问题用红笔做好标记。

【学习过程】一、预习案1.思考一元二次方程)0(02≠=++a c bx ax 的根与二次函数)0(2≠++=a c bx ax y 的图象有什么关系？2.判断下列方程是否有根，有几个实数根？（1）0322=--x x （2）0122=+-x x （3）0322=+-x x3.画出与以上方程对应的二次函数图象，观察方程的根与图象和x 轴交点坐标的关系。

4.零点的定义：对于函数y =f (x ),我们把使 叫做函数y =f (x )的零点。

思考1：零点是点吗？思考2：尝试归纳总结一元二次函数零点的情况。

xoy 二、探究案1.例1：求函数 )16()(2-=x x x f 的零点。

2.例2：:函数)(x f y 图象如下，求其零点。

三、训练案跟踪练习1：求以下函数的零点。

(1)12)(-=x x f (2) 67)(2+-=x x x f (3))10(log )(≠>=a a x x f a 且跟踪练习2：1.函数)(x f y =图象如下，求其零点。

2.下列图象表示的函数中没有零点的是（ ）3.已知函数 m x x f +-=2)(的零点为4，则实数m 的值为（ ）。

A.-6B.8C.23D.23- 4.已知函数f (x )是定义域为R 的奇函数，且 f (x )在（0，+∞）有一个零点，则f (x )的零点个数为_____。

【学习反思】。