均匀带电圆盘轴线上一点的场强

1图 1图2三种均匀带电的圆面中心轴线上的电场强度赏析——兼析三道高考选择题周林（宁波市鄞州区正始中学， 浙江 宁波 315131）近几年高考题中，有些问题的结论不一定必须通过计算才能验证，有时只需通过一定的物理分析就可以判断结论是否正确。

因此，不仅要提升物理关系式的分析鉴别能力，而且更要挖掘出其中蕴含的物理思想和方法。

让学生知其然还要知其所以然，本文拟用高等数学的定积分推导出三种均匀带电的圆面中心轴线上的电场强度的表达式，并分析三道高考选择题。

模型1：均匀带电的圆圈中心轴线上的电场强度如图1所示，均匀带电且单位长度带电量为λ的一个半径为R 的圆圈，求其中心轴线上任意一点P （坐标为x ）的电场强度在圆环上选取长为dl 的带电微元圆弧，根据点电荷的电场强度，在点P 产生的电场方向与x 轴的夹角为θ，沿x 轴方向的大小为θλcos 22xR dlkdE +=2222xR x xR dlk+⨯+=λ()2322xRxdlk +=λ由定积分得 ()232220xRxdlk E R +=⎰λπ ()23222xRxkR +=λπ根据对称性和叠加性，均匀带电圆圈在点P 产生的合场强必沿x 轴方向，正负由电荷符号决定，大小为()23222xRxkR E +=λπ。

若均匀带电圆圈的电量为q ，即λπR q 2=，则()2322xRkqxE +=。

讨论1：（1）当x 《R 时，则E =0，相当于圆圈中心处的场强，根据对称性可得场强为零。

（2）当x 》R 时，则2xkqE =，相当于点电荷的场强。

若x →∞时，则有E →0。

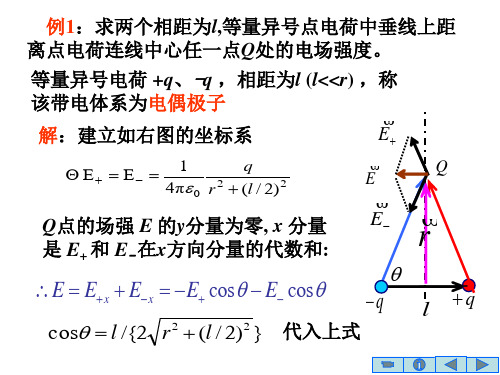
模型拓展1：两个彼此平行且共轴的均匀带电圆圈中心轴线上的电场强度 （1）两圆圈带同种电荷例1：（2010年福建卷）物理学中有些问题的结论不一定必须通过计算才能验证，有时只需通过一定的分析就可以判断结论是否正确。

如图2所示为两个彼此平行且共轴的半径分别为R 1和R 2的圆环，两圆环上的电荷量均为q (q >0)，而且电荷均匀分布。

带电圆环在轴线上一点的场强最大值带电圆环在轴线上一点的场强最大值1. 带电圆环的场强分布带电圆环是一个非常常见的电荷分布方式，在物理学中经常涉及到。

当我们想要计算带电圆环在轴线上一点的场强时，可以利用电场叠加原理来进行分析。

2. 场强计算公式带电圆环在轴线上一点的场强计算公式是一个复杂的积分表达式，需要通过对圆环上各个微小电荷的贡献进行积分求和来得到。

这个公式是由以往的物理学家通过数学推导得到的，数学形式较复杂，我们可以简单描述一下其形式。

3. 场强最大值出现的位置在带电圆环的轴线上，场强的最大值出现在圆环中心对应的轴线位置上。

这是一个非常重要的结论，在实际问题中会经常涉及到。

4. 场强最大值的计算对于带电圆环在轴线上一点的场强最大值，我们可以通过对场强公式进行求导来得到。

这样可以找到场强最大值出现的位置，以及最大值的大小。

5. 物理实际意义的思考在对带电圆环在轴线上一点的场强最大值进行计算和分析的过程中，我们不仅可以学习到物理学的具体计算方法，还能深入思考带电圆环的场强分布特点、电场的性质及其在现实中的应用和意义。

总结与回顾：带电圆环在轴线上一点的场强最大值是一个基础而又重要的物理学问题。

通过对这个问题的深入研究，我们可以学习到电场的计算方法、场强分布的特点，以及利用数学工具解决物理实际问题的能力。

在我的个人观点中，我认为通过深入学习和思考这个问题，可以帮助我们更好地理解电场的性质，进而应用到工程技术等现实问题中。

这也能培养我们的数学建模和物理实际问题解决的能力。

通过对带电圆环在轴线上一点的场强最大值的研究，我们可以更全面、深刻地理解电场理论，并且在这个过程中锻炼我们的思维和动手能力。

希望这篇文章能够帮助你更好地理解这个问题，并且在今后的学习和工作中有所启发。

带电圆环在轴线上一点的场强最大值是一个重要且复杂的物理问题，在物理学的学习和研究中具有重要意义。

这个问题涉及到电荷分布、电场计算、数学建模等多个方面，通过深入研究这个问题，我们可以更好地理解电场的性质，并且为解决实际问题提供理论支持。

122科技资讯 SC I EN C E & TE C HN O LO G Y I NF O R MA T IO N动力与电气工程电磁学的基本内容之一就是对于均匀带电体的场强和电势的计算,电磁学的相关书中均有详细的介绍[1～4]。

然而对于均匀带电体中某些特殊点的场强与电势的问题却没有详细地讨论,而关于这些特殊点的场强与电势的理解又是非常重要的。

本文通过均匀带电体的电势与场强的求解过程来讨论这些特殊点的场强与电势。

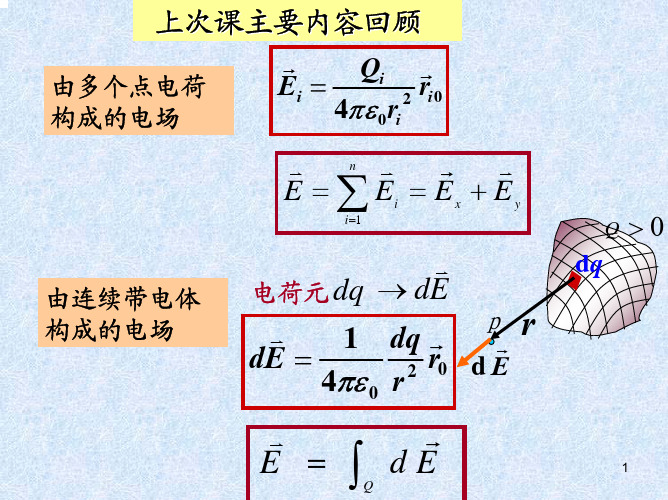
1 均匀带电体的场强与电势将均匀带电体分割成无数多个电荷元dq,每一个电荷元dq可以看作一点电荷,点电荷在空间某点P产生的场强dE和电势dU 分别为:0204dq dE r r和04dq dU r 。

其中0r为电荷元dq到P点的矢径 r方向的单位矢量。

根据场强叠加原理和电势叠加原理,整个带电体在P点产生的总场强和总电势分别为:0204VVdqE dE r r和04V dq U dU r 。

若电荷连续分布在一体积内,用ρ表示电荷体密度,则式中dq dV ;若电荷连续分布在一曲面或平面上,用σ表示电荷面密度,则dq ds ;若电荷连续分布在一曲线或直线上,用λ表示电荷线密度,则dq dl 。

相应地计算总场强E和总电势 U 的积分分别为体积分、面积分和线积分。

2 均匀带电圆环和圆盘轴线上的场强真空中一均匀带电圆环,环半径为R,带电量q,圆环轴线上任一点P的场强。

首先取环的轴线为坐标x轴,轴上P点与环心的距离为x 。

在圆环上取线元d l ,它与P 点的距离为r ,如图1所示,则:2qdq dl dl R。

dq 在P点产生的场强dE 的方向如图,大小为204dl dE r 。

dE 与x轴平行的分量://20cos 4dl dE r 。

dE 与x轴垂直的分量:20sin 4dldE r 。

根据对称性可知,带电圆环上在同一直径两端取相等的电荷元在P点产生的场强垂直于x轴方向的分量相互抵消,所以P点的总场强方向沿x轴正向,即:23/22230220000cos 4444R L L L dl dl x x qxE dE dl r r r r R x 当0q 时,E沿x轴离开原点O的方向;当0q 时,E沿x轴指向原点O的方向。

带电圆环在轴线上一点的场强公式推导带电圆环在轴线上一点的场强公式推导，是物理学中非常经典的问题之一。

下面，我们将从电荷密度、高斯定律和积分等方面，逐步推导出这个公式。

具体步骤如下：1. 首先，我们需要明确带电圆环上的电荷密度。

根据定义，电荷密度是单位体积内的电荷量。

因此，对于一个半径为R、总电荷量为Q的圆环而言，它的电荷密度可以表示为：$\rho = \frac{Q}{V} = \frac{Q}{\frac{4}{3}\pi R^3}$2. 接下来，我们将运用高斯定律求出圆环在轴线上一点的电场强度。

由于我们关心的是轴线上的场强，因此选择以轴线为对称轴作为高斯面。

此时，高斯面穿过圆环，且由于对称性，高斯面上电场强度只有沿着轴线方向的分量。

3. 我们可以通过高斯定律，将圆环内部的电场强度与高斯面的电通量联系起来：$\oint_S \textbf{E} \cdot \textbf{dS} = \frac{Q_{enc}}{\epsilon_0}$其中，$Q_{enc}$为高斯面包围的电荷量，$\epsilon_0$为真空介电常数。

4. 接下来，我们需要计算高斯面上的电通量。

由于高斯面与圆环的交线垂直于轴线，因此高斯面的面积可以表示为：$S = 2\pi Rz$其中，z为高斯面距离圆环中心的距离。

5. 高斯面上的电通量可以表示为：$\oint_S \textbf{E} \cdot \textbf{dS} = \int_{-z_0}^{z_0} E_z \cdot 2\pi Rz \cdot dz$其中，$z_0$为高斯面与圆环的交点到圆环中心的距离。

由于我们只考虑沿着轴线方向的电场强度分量，因此上式中仅存在$E_z$。

6. 对于圆环内部的电荷，可以根据库伦定律计算出与圆环交点距离为z 的电荷在轴线上产生的电场强度：$dE = \frac{1}{4\pi\epsilon_0} \frac{\rho dl}{r^2}$其中，$dl$为圆环上的电荷微元长度，r为电荷到轴线的距离。

均匀带电圆盘轴线上的电场强度可以通过库仑定律来计算。

假设我们有一个半径为R的均匀带电圆盘，电荷面密度为σ，我们想要在盘的轴线上计算电场强度。

在轴线上选取一个与盘中心重合的点作为参考点。

假设我们要计算离盘中心距离为z处的电场强度。

根据库仑定律，轴线上的电场强度可以由下式给出：
E = (1 / (4πε₀)) * (2πσz / (z²+ R²)^(3/2))
其中，ε₀是真空中的介电常数（ε₀≈8.854 ×10^(-12) C²/(N·m²))。

这个公式表明，轴线上的电场强度随着离盘中心距离z的增加而减小。

当z远大于R时，电场强度的减小趋势变得更加明显。

需要注意的是，当z = 0时，即在圆盘上的中心点上，由于对称性的原因，电场强度为零。

而在z = R时，即在圆盘上的表面上，电场强度为最大值。