编译原理第4章答案

procedure T; begin if sym=ˊ(ˊor sym=ˊaˊ or sym=ˊbˊ or sym=ˊ∧ˊ then begin F; T end else error end;
（4）构造它的递归下降分析程序。
procedure T ; begin
if sym= ˊ(ˊ or sym= ˊaˊ or sym= ˊbˊ or sym= ˊ∧ˊ then T else if sym= ˊ*ˊ then error end;
（3）该文法不含左递归，而且每一个 非终结符的各个产生式的候选首符集两 两不相交。
FIRST(A)= {a}
FOLLOW(A)={d, #}
FIRST (A) = { ε, a} FOLLOW(A)={d, #}
FIRST(B) = {d} FOLLOW(B )={e}
FIRST(B) = {ε ,b} 法G ’
(S): S → a∣∧∣(T) T → ST ’ T’ → ,ST’ | ε
其中：过程advance把输入串指示器IP调至指向下一个输入 符号；sym是指IP当前所指的那个输入符号；error为出错诊 断处理程序。
（2）经改写后的文法是否是LL(1)的？给出它的预测分析表。
else error end else error end;
4.2 试消除下面文法G[A] 中的左递归，并提取公共左因子， 判断改写后的文法是否为LL(1)文法?
A→aABe∣a
B→Bb∣d
解: （1）首先消除左递归
A→aABe∣a B →dB B →bB | ε （2）提取公共左因子 A → aA A → ABe | ε B → dB B →bB | ε
证明：对于具有形如A|的产生式有： A → ABe | ε B →bB | ε

第三章习题解答6．每个表达式的推导及语法树分别如下：(1) <表达式>=> <项>=> <因子>=> i(2) <表达式>=> <项>=><因子>=>(<表达式>)=>(<项>)=>(<因子>)=>(i)(3) <表达式>=> <项>=><项>*<因子>=><因子>*<因子>=>i*<因子>=>i*i(4) <表达式>=> <表达式>+<项>=> <项>+<项>=> <项>*<因子>+<项>=> <因子>*<因子>+<项>=> i*<因子>+<项>=> i*i+<项>=> i*i+<因子>=> i*i+i(5) <表达式>=> <表达式>+<项>=> <项>+<项>=> <因子>+<项>=> i+<项>=> i+<因子>=>i+<表达式>=>i+(<表达式>+<项>)=> i+(<项>+<项>)=> i+(<因子>+<项>)=> i+(i+<项>)=> i+(i+<因子>)=>i+(i+i)(6) <表达式>=> <表达式>+<项>=> <项>+<项>=> <因子>+<项>=> i+<项>=> i+<项>*<因子>=> i+<因子>*<因子>=> i+i*<因子>=> i+i*i<表达式> <项> <因子>i<表达式><项><因子>()<表达式><项><因子>i<表达式><项>*<项><因子><因子>ii图（1）图（2）图（3）()<表达式><表达式><表达式><项>+<项>*<项><因子><因子>i<因子>ii <表达式><表达式><项>+<项><因子><因子>i<表达式><项>+<项><因子>i <因子>i图（4）图（5）<表达式><表达式><项>+<项><因子>i图（6）*<项><因子><因子>i i11．根据文法G 给定的规则，从文法的开始符E 出发可推导出E+T*F ，推导过程如下：E => E+T => E+T*F ，所以E+T*F 是该文法的一个句型。

第五章习题5-1设有文法G[S] ：S→A/A→aA∣ AS∣/(1)找出部分符号序偶间的简单优先关系。

(2)验证 G[S] 不是简单优先文法。

5-2对于算符文法G[S] ：S→E E→ E-T∣ T T→T*F∣F F→ -P∣P P→ (E)∣i(1)找出部分终结符号序偶间的算符优先关系。

(2)验证 G[S] 不是算符优先文法。

5-3 设有文法G′[E] ：E→E E→E+T |T1T →T T→T*F|F F→(E)|i11111其相应的简单优先矩阵如题图5-3所示，试给出对符号串（i+i ）进行简单优先分析的过程。

题图 5-3 文法 G′ [E] 的简单优先矩阵5-4设有文法G[E]：E→E+T|TT→T*F|FF→(E)|i其相应的算符优先矩阵如题图5-4 所示。

试给出对符号串（i+i ）进行算符优先分析的过程。

(i*+)#(○○○○○＜＜＜＜＝i○○○○＞＞＞＞○○○○○○*＜＜＞＞＞＞○○○○○○+＜＜＜＞＞＞○○○○)＞＞＞＞○○○○#＜＜＜＜题图 5-4文法 G[E] 的算符优先矩阵5-5对于下列的文法，试分别构造识别其全部可归前缀的DFA和 LR(0) 分析表，并判断哪些是LR(0) 文法。

(1)S →aSb∣ aSc∣ ab(2)S →aSSb∣ aSSS∣c(3)S →AA→Ab∣ a5-6下列文法是否是SLR(1)文法？若是，构造相应的SLR(1) 分析表，若不是，则阐明其理由。

(1) S →Sab∣ bR R→S∣a(2) S →aSAB∣ BA A→aA∣ B B→ b(3) S →aA∣bB A→cAd∣εB→cBdd∣ε5-7对如下的文法分别构造LR(0) 及 SLR(1) 分析表，并比较两者的异同。

S→cAd∣ b A→ASc∣a5-8对于文法G[S]:S→A A→BA∣εB→ aB∣ b(1)构造 LR(1) 分析表；(2)给出用LR(1)分析表对输入符号串abab 的分析过程。

注意：本题应该理解为对图(a)进行确定化和对图(b)进行最小化。提供的答案没有对图(a)确 定化。
盛威网（）专业的计算机学习网站 14
《编译原理》课后习题答案第四章
第5题 构造一个 DFA，它接收 Σ={0,1}上所有满足如下条件的字符串：每个 1 都有 0 直接跟在 右边。并给出该语言的正规式。 答案： 按题意相应的正规表达式是(0*10)*0*， 或 0*(0 | 10)*0* 构造相应的 DFA， 首先构造 NFA 为
7
《编译原理》课后习题答案第四章
注意：这个题，也可以这样构造 NFA（用最少的ε，但注意不能出错） ：
a,b 0 a a 2 a,b 1 a b 3
盛威网（）专业的计算机学习网站
8
《编译原理》课后习题答 ε X b A ε F B a C b ε b G b H ε ε D ε E a I b Y
除 X，A 外，重新命名其他状态，令 AB 为 B、AC 为 C、ABY 为 D，因为 D 含有 Y（NFA 的终态），所以 D 为终态。 . X A B C D DFA 的状态图：: 0 . A C A C 1 A B B D B
(2)先构造 NFA： 0 ε X 1 A ε ε F B 1 C 1 0 ε 0 D 1 E 1 0 ε 用子集法将 NFA 确定化 ε X T0=X A T1= ABFL Y CG T2= Y T3= CGJ DH K T4= DH EI T5= ABFKL T6= ABEFIL EJY T7= ABEFGJLY EHY CGK T8= ABEFHLY EY CGI T9= ABCFGJKL DHY T10= ABEFLY T11= CGJI DHJ T12= DHY T13= DHJ EIK T14= ABEFIKL ABEFIKL EJY CG DHJ ？正确 DHJG EI EIK DHY EY DHJ CG K ABEFLY CGJI DHY CGK ABEFHLY ABCFGJKL EY CGI ABEFGJLY EHY CGK ABEFIL Y EJY CG CG DH ABFKL EI DH K Y CGJ ABFL Y CG X A 0 1 1 ε L ε K ε J 0 Y

编译原理第四章参考答案1.1考虑下⾯⽂法G1S->a|^|(T)T->T,S|S消去G1的左递归。

然后对每个⾮终结符，写出不带回溯的递归⼦程序。

答:：(1)消除左递归:S->a|^|(T)T-> ST’T’->,S T’|ε(2)first(S)={ a , ^ , ( } first(T)= { a , ^ , ( } first(T’)={ , ε}First(a)={a},First(^)={^},First( (T) )={ ( }S的所有候选的⾸符集不相交First(,ST’)={,} ,First(ε)={ε},T’的所有候选的⾸符集不相交Follow(T’)=Follow(T)={ )}first(T’)∩Follow(T’)={}所以改造后的⽂法为LL(1)⽂法。

不带回溯的递归⼦程序如下：S( ){if (lookahead=’a’) advance;Else if(lookahead=’^’) advance;Else if(lookahead=’(’){advance;T();if(lookahead=’)’) advance;else error();}Else error();}T( ){S( );T’( ):}T’->,S T’|εT’( ){if (lookahead=’,’){advance;T’();}Else if(lookahead=Follow(T’)) advance;Else error;}有⽂法G(S):S→S+aF|aF|+aFF→*aF|*a(1)改写⽂法为等价⽂法G[S’]，消除⽂法的左递归和回溯(2)构造G[S’]相应的FIRST和FOLLOW集合；(3)构造G[S’]的预测分析表，以此说明它是否为LL(1)⽂法。

(4)如果是LL(1)⽂法，请给出句⼦a*a+a*a*a的预测分析过程该⽂法为LL(1)⽂法，因为它的预测分析表中⽆冲突项。

Lw.《编译原理》课后习题答案第一章第1章引论第1题解释下列术语：（1）编译程序（2）源程序（3）目标程序（4）编译程序的前端（5）后端（6）遍答案：（1）编译程序：如果源语言为高级语言，目标语言为某台计算机上的汇编语言或机器语言，则此翻译程序称为编译程序。

（2）源程序：源语言编写的程序称为源程序。

（3）目标程序：目标语言书写的程序称为目标程序。

（4）编译程序的前端：它由这样一些阶段组成：这些阶段的工作主要依赖于源语言而与目标机无关。

通常前端包括词法分析、语法分析、语义分析和中间代码生成这些阶段，某些优化工作也可在前端做，也包括与前端每个阶段相关的出错处理工作和符号表管理等工作。

（5）后端：指那些依赖于目标机而一般不依赖源语言，只与中间代码有关的那些阶段，即目标代码生成，以及相关出错处理和符号表操作。

（6）遍：是对源程序或其等价的中间语言程序从头到尾扫视并完成规定任务的过程。

第2题一个典型的编译程序通常由哪些部分组成？各部分的主要功能是什么？并画出编译程序的总体结构图。

答案：一个典型的编译程序通常包含8个组成部分，它们是词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、中间代码优化程序、目标代码生成程序、表格管理程序和错误处理程序。

其各部分的主要功能简述如下。

词法分析程序：输人源程序，拼单词、检查单词和分析单词，输出单词的机内表达形式。

语法分析程序：检查源程序中存在的形式语法错误，输出错误处理信息。

语义分析程序：进行语义检查和分析语义信息，并把分析的结果保存到各类语义信息表中。

中间代码生成程序：按照语义规则，将语法分析程序分析出的语法单位转换成一定形式的中间语言代码，如三元式或四元式。

中间代码优化程序：为了产生高质量的目标代码，对中间代码进行等价变换处理。

盛威网（）专业的计算机学习网站1《编译原理》课后习题答案第一章目标代码生成程序：将优化后的中间代码程序转换成目标代码程序。

表格管理程序：负责建立、填写和查找等一系列表格工作。

也称基地址。 SL： 静态链，指向定义该过程的直接外过程（或主程序）运行时最新数据段的基地址，
用以引用非局部（包围它的过程）变量时，寻找该变量的地址。 DL： 动态链，指向调用该过程前正在运行过程的数据段基地址，用以过程执行结束释放
数据空间时，恢复调用该过程前运行栈的状态。 RA： 返回地址，记录调用该过程时目标程序的断点，即调用过程指令的下一条指令的地
编译程序大致有哪几种开发技术？
答案：
（1）自编译：用某一高级语言书写其本身的编译程序。 （2）交叉编译：A 机器上的编译程序能产生 B 机器上的目标代码。 （3）自展：首先确定一个非常简单的核心语言 L0，用机器语言或汇编语言书写出它的编
译程序 T0，再把语言 L0 扩充到 L1，此时 L0⊂ L1 ,并用 L0 编写 L1 的编译程序 T1，再把语 言 L1 扩充为 L2，有 L1 ⊂ L2 ,并用 L1 编写 L2 的编译程序 T2，……，如此逐步扩展下 去， 好似滚雪球一样，直到我们所要求的编译程序。 （4）移植：将 A 机器上的某高级语言的编译程序搬到 B 机器上运行。
(main).
答案： 程序执行到赋值语句 b∶=10 时运行栈的布局示意图为：
1
《编译原理》课后习题答案第二章
第 3题 写出题 2 中当程序编译到 r 的过程体时的名字表 table 的内 容。
name
kind
level/val
adr
size
答案：
题 2 中当程序编译到 r 的过程体时的名字表 table 的内容为：
盛威网（）专业的计算机学习网站
2
《编译原理》课后习题答案第一章
合实现方案，即先把源程序翻译成较容易解释执行的某种中间代码程序，然后集中解释执行 中间代码程序，最后得到运行结果。

编译原理课后答案（第三版蒋立源康慕宁编）第一章习题解答1解：源程序是指以某种程序设计语言所编写的程序。

目标程序是指编译程序（或解释程序）将源程序处理加工而得的另一种语言（目标语言）的程序。

翻译程序是将某种语言翻译成另一种语言的程序的统称。

编译程序与解释程序均为翻译程序，但二者工作方法不同。

解释程序的特点是并不先将高级语言程序全部翻译成机器代码，而是每读入一条高级语言程序语句，就用解释程序将其翻译成一段机器指令并执行之，然后再读入下一条语句继续进行解释、执行，如此反复。

即边解释边执行，翻译所得的指令序列并不保存。

编译程序的特点是先将高级语言程序翻译成机器语言程序，将其保存到指定的空间中，在用户需要时再执行之。

即先翻译、后执行。

2解：一般说来，编译程序主要由词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、代码优化程序、目标代码生成程序、信息表管理程序、错误检查处理程序组成。

3解：C语言的关键字有：auto break case char const continue default do double else enum extern float for goto if int long register return short signed sizeof static struct switch typedef union unsigned void volatile while。

上述关键字在C语言中均为保留字。

4解：C语言中括号有三种：{}，[]，（）。

其中，{}用于语句括号；[]用于数组；（）用于函数（定义与调用）及表达式运算（改变运算顺序）。

C语言中无END关键字。

逗号在C语言中被视为分隔符和运算符，作为优先级最低的运算符，运算结果为逗号表达式最右侧子表达式的值（如：(a,b,c,d)的值为d）。

5略第二章习题解答1.（1）答：26*26=676（2）答：26*10=260（3）答：{a,b,c,...,z,a0,a1,...,a9,aa,...,az,...,zz,a00,a01,...,zzz},共26+26*36+26*36*36=34658个2.构造产生下列语言的文法（1）{anbn|n≥0}解：对应文法为G(S) = ({S},{a,b},{ S→ε| aSb },S)（2）{anbmcp|n,m,p≥0}解：对应文法为G(S) = ({S,X,Y},{a,b,c},{S→aS|X,X→bX|Y,Y→cY|ε},S)（3）{an # bn|n≥0}∪{cn # dn|n≥0}解：对应文法为G(S) = ({S,X,Y},{a,b,c,d,#}, {S→X, S→Y,X→aXb|#,Y→cYd|# },S)（4）{w#wr# | w?{0,1}*,wr是w的逆序排列}解：G(S) = ({S,W,R},{0,1,#}, {S→W#, W→0W0|1W1|# },S)（5）任何不是以0打头的所有奇整数所组成的集合解：G(S) = ({S,A,B,I,J},{-,0,1,2,3,4,5,6,7,8,9},{S→J|IBJ,B→0B|IB|e, I→J|2|4|6|8, Jà1|3|5|7|9}, S)（6）所有偶数个0和偶数个1所组成的符号串集合解：对应文法为S→0A|1B|e，A→0S|1C B→0C|1S C→1A|0B3.描述语言特点（1）S→10S0S→aAA→bAA→a解：本文法构成的语言集为：L(G)={(10)nabma0n|n, m≥0}。

第4章练习P72作业布置：P723，7，9，11提示1：判断两个正规式是否相等，应判断两个正规式所产生的正规集是否一样。

完成此项任务需要经过四个阶段：第一，画出正规式的NFA；第二，由NFA变换到DFA；第三，将DFA最小化；第四，画出最小化DFA的有限自动机。

如果要判断的正规式的最小化DFA的有限自动机是一样的，则正规式等价；反之，则不等价。

提示2：构造正规表达式的最小化的DFA方法是：首先，按规则将正规表达式用NFA表示；其次，使用ε-closure(Move())将NFA转变为DFA；最后使用子集法将DFA最小化。

对于这类题目要多做练习，熟能生巧。

3.将下图确定化：解：下表由子集法将NFA 转换为DFA ：7、给文法G[S]： S →aA|bQ A →aA|bB|bB →bD|aQ0，10，1Q →aQ|bD|b D →bB|aA E →aB|bFF →bD|aE|b构造相应的最小的DFA 。

解：由于从S 出发任何输入串都不能到达状态E 和F ，所以，状态E ，F 为多余的状态，不予考虑。

这样，可以写出文法G[S]对应的NFA M ：NFA M={k, Σ, f, S, Z}K={S, A, B, Q, D, Z} S={S} Z={Z} F(S, a)=A f(S, b)=Q F(A, a)=A f(A, b)=B f(A,b)=ZF(B, b)=D f(B, a)=QF(Q, a)=Q f(Q, b)=D f(Q,b)=Z F(D, b)=B f(D, a)=A NFA M 的状态转换图为：下表由子集法将NFA 转换为DFA ：a由上表可知：(1)因为C、D是DFA的终态，其他是非终态，可将状态集分成两个子集：P1={S, A, B, E, F}，P2={C, D}。

(2)因为{A, B}b={C, D}为终态，{S, E, F}b={B, E, F}为非终态，所以P1可划分为：P11={S, E, F}，P12={A, B}。

3、一个上下文无关文法生成句子 abbaa 的推导树如下： (1)给出串 abbaa 最左推导、最右推导。 (2)该文法的终结符、非终结符、产生式集合 P 可能有哪些元素？ (3)找出该句子的所有短语、直接短语、句柄。
提示：知识点：语法树的构造，文法的组成，短语等概念。
4、给出生成下述语言的三型文法：{anbmck|n, k>=1，m>0 } 提示：（1）三型文法中产生式的特点 （2）可参考P49 第16题
第四章 知识结构
⑤ 正规文法
② 正规式
③
有穷自动机（NFA
DFA)
④
{正规集}
①
⑥
词法分析
自动构造工具
1、已知正规式b(ab)*和(ba)*b (1)分别构造上述两个正规式相应的DFA， (2) 将(1)构造的DFA最小化， (3)利用DFA证明b(ab)*=(ba)*b (4)构造该语言的正规文法。
提示： 使用的知识点：正规式 NFA，NFADFA，DFA的最小 化，DFA 正规文法。 由转化得到的相同的最小化DFA，进而证明两个正规式 等价。
2、(1)由偶数个0和奇数个1构成的所有01串的ＤＦＡ。 （2）写出由0和1的个数都是偶数的01串的正规式。 提示：见下页PPT
参考课件 例2：接受0和1的个数都是偶数的字符串的DFA
提示：（1）生成的偶正数应不包括，若干个0。 （2）将偶正数分为两类：一类为允许若干个0（0个数>=0）后跟不以0开头 的偶正数；一类为允许若干个0后跟2|4|6|8的偶正数（如0002，即不允许只含 有若干0 ）。 2、为只包含数字、 , 的表达式，例如 9 2 5等构造一个文法，使得 和 运算满足右结合， 的运算优先级高于。 提示：结合性和运算优先性可以根据语法树的层次考虑。进而思考左递归产 生式与运算符的结合性的关系。

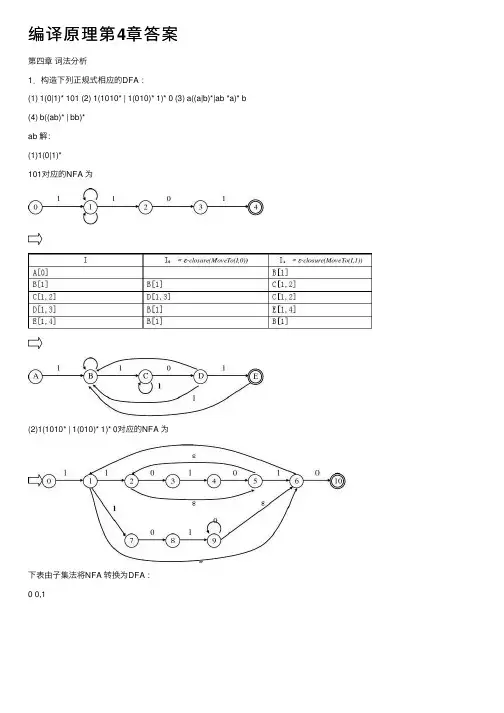
编译原理第4章答案第四章词法分析1．构造下列正规式相应的DFA ：(1) 1(0|1)* 101 (2) 1(1010* | 1(010)* 1)* 0 (3) a((a|b)*|ab *a)* b (4) b((ab)* | bb)*ab 解：(1)1(0|1)*101对应的NFA 为(2)1(1010* | 1(010)* 1)* 0对应的NFA 为下表由⼦集法将NFA 转换为DFA ：0 0,1(3)a((a|b)*|ab*a)* b (略)(4)b((ab)* | bb)* ab (略)2．已知NFA=（{x,y,z},{0,1},M,{x},{z}）其中：M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA。

解：根据题意有NFA图如下0，1 下表由⼦集法将NFA转换为DFA：下⾯将该DFA最⼩化：(1)⾸先将它的状态集分成两个⼦集：P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F，C等价。

由于F(B,0)=F(C,0)=C, F(B,1)=D,F(C,1)=E,⽽D，E不等价（见下步），从⽽B与C，F可以区分。

有P21={C,F},P22={B}。

(3)区分P1:由于A，E输⼊0到终态，⽽D输⼊0不到终态，所以D与A，E可以区分，有P11={A,E},P12={D}。

(4)由于F(A,0)=B,F(E,0)=F,⽽B，F不等价，所以A，E可以区分。

(5)综上所述，DFA可以区分为P={{A}，{B}，{D}，{E}，{C，F}}。

所以最⼩化的DFA如下：3.将图4.16确定化：图4.16解：下表由⼦集法将NFA转换为DFA：14.把图4.17的(a)和(b)分别确定化和最⼩化：(a) (b)解： (a):下表由⼦集法将NFA 转换为DFA ：可得图（a1），由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价，可将DFA 最⼩化，即：删除B ，将原来引向B 的引线引向与其等价的状态A ，有图(a2)。

蒋⽴源编译原理第三版第四章习题与答案第4章习题14-1 消除下列⽂法的左递归性。

(1) S→SA|A A→SB|B|(S)|( ) B→[S]|[ ](2) S→AS|b A→SA|a(3) S→(T)|a|ε T→S|T,S4-2 对于如下⽂法，求各候选式的FIRST集和各⾮终结符号的FOLLOW集。

S→aAB|bA|ε A→aAb|ε B→bB|ε4-3 验证下列⽂法是否为LL(1)⽂法。

(1) S→AB|CDa A→ab|c B→dE|εC→eC|ε D→fD|f E→dE|ε(2) S→aABbCD|ε A→ASd|ε B→SAc|eC|εC→Sf|Cg|ε D→aBD|ε4-4 对于如下的⽂法G[S]：S→Sb|Ab|bA→Aa|a(1) 构造⼀个与G等价的LL(1)⽂法G′[S]；(2) 对于G′[S]，构造相应的LL(1)分析表；(3) 利⽤LL(1)分析法判断符号串aabb是否是⽂法G[S]的合法句⼦。

4-5 设已给⽂法S→SaB|bB A→S|a B→Ac(1) 构造⼀个与G等价的LL(1)⽂法G′[S]；(2) 对于G′[S]，构造相应的LL(1)分析表；(3) 利⽤LL(1)分析法判断符号串bacabc是否是⽂法G[S]的合法句⼦。

第4章习题答案4-1 解：(1) ⽂法G[S]中的S，A都是间接左递归的⾮终结符号。

将A产⽣式的右部代⼊产⽣式S→A中，得到与原⽂法等价的⽂法G′[S]：S→SA|SB|B|(S)|( )A→SB|B|(S)|( )B→[S]|[ ]⽂法G′[S]中的S是直接左递归的⾮终结符号，则消除S产⽣式的直接递归性后，我们便得到了与原⽂法等价且⽆任何左递归性的⽂法G"[S]：S→BS′|(S)S′|( )S′A→SB|B|(S)|( )B→[S]|[ ](2) ⽂法G[S]中的S，A都是间接左递归的⾮终结符号。

将A产⽣式代⼊产⽣式S→AS中，得到与原⽂法等价的⽂法G′[S]：S→SAS|aS|bA→SA|a⽂法G′[S]中的S是直接左递归的⾮终结符号，则消除S产⽣式的直接递归性后，我们便得到了与原⽂法等价且⽆任何左递归性的⽂法G"[S]：S→aSS′|bS′S′→ASS′|εA→SA|a(3) ⽂法G[S]中的T是直接左递归的⾮终结符号。

“编译技术”第四章作业4-1 已知文法G[C]：C→iEtS|iEtSeSE→ a|bS→ a+b|a*b(1)提取左公共因子；(2)计算修改后文法的每个非终结符的FIRST集和FOLLOW集；(3)给出递归下降分析程序。

(3)递归下降分析程序void match(token t){if(lookahead=='t')lookahead = nexttoken;else error;}void C(){if(lookahead=='i'){match('i');E();if(lookahead=='t'){match('t');S();Cprime();}else error;}else error;}void Cprime(){if(lookahead=='e'){match('e');S();}}void E(){if(lookahead=='a')match('a');else if(lookahead=='b')match('b');else error;}void S(){if(lookahead=='a'){match('a');Sprime();}}void Sprime(){if (lookahead=='+'){match('+');if(lookahed=='b'){match('b');}else error();}else if(lookahead=='*'){match('*');if(lookahead=='b'){match('b');}else error();}}4-2 已知文法G[Z]：Z→Az|bA→ Za|a(1)删除左递归；(2)计算修改后文法的每个非终结符的FIRST集和FOLLOW集；(3)给出递归下降分析程序。

2）文法： S SS | SS* | a 输入串：aaa*a++ 自底向上语法分析过程：
c.消除左递归：S->aS’ S’->SAS’|Ɛ A->+|*
代入
S->aS’ S’->aS’AS’|Ɛ A->+|*
d.得到的文法适用于自顶向下的语法分析吗？ 适用。因为文法中不存在左公因子，也不存在左递归
4.4.3 S->SS+|SS*|a
FIRST(S)={a}
因为S是起始符号，把{$}加入到Follow(S)中。 对于S->SS+的第一个S，把First(S+) = {a}加入到Follow(S)中。 对于S->SS*的第一个S，把First(S*) = {a}加入到Follow(S)中。 对于S->SS+的第二个S，把First(+) = {+}加入到Follow(S)中。 对于S->SS*的第二个S，把First(*) = {*}加入到Follow(S)中。 所以，FOLLOW(S)={a,+,*,$}
S A| B A AA | E0E （A是0比1多的串） B BB | E1E （B是1比0多的串） E 0E1E | 1E0E | （E是0和1的个数相等的串）
5）所有由0和1组成的且其中不包含子串011的串的集合。
S AB A 1 A | B 0 B | 01 B |
6）所有由0和1组成的形如xy的串的集合，其中 x y 且x和y等长。 S AB | BA A XAX | 0 （A是奇数长度，中间为0的串） B XBX | 1 （B是奇数长度，中间为1的串） X0|1

编译原理习题及答案（整理后）第⼀章1、将编译程序分成若⼲个“遍”是为了。

b．使程序的结构更加清晰2、构造编译程序应掌握。

a．源程序b．⽬标语⾔c．编译⽅法3、变量应当。

c．既持有左值⼜持有右值4、编译程序绝⼤多数时间花在上。

d．管理表格5、不可能是⽬标代码。

d．中间代码6、使⽤可以定义⼀个程序的意义。

a．语义规则7、词法分析器的输⼊是。

b．源程序8、中间代码⽣成时所遵循的是- 。

c．语义规则9、编译程序是对。

d．⾼级语⾔的翻译10、语法分析应遵循。

c．构词规则⼆、多项选择题1、编译程序各阶段的⼯作都涉及到。

b．表格管理c．出错处理2、编译程序⼯作时，通常有阶段。

a．词法分析b．语法分析c．中间代码⽣成e．⽬标代码⽣成三、填空题1、解释程序和编译程序的区别在于是否⽣成⽬标程序。

2、编译过程通常可分为5个阶段，分别是词法分析、语法分析中间代码⽣成、代码优化和⽬标代码⽣成。

3、编译程序⼯作过程中，第⼀段输⼊是源程序，最后阶段的输出为标代码⽣成程序。

4、编译程序是指将源程序程序翻译成⽬标语⾔程序的程序。

⼀、单项选择题1、⽂法G：S→xSx|y所识别的语⾔是。

a. xyxb. (xyx)*c. x n yx n(n≥0)d. x*yx*2、⽂法G描述的语⾔L(G)是指。

a. L(G)={α|S+?α , α∈V T*}b. L(G)={α|S*?α, α∈V T*}c. L(G)={α|S*?α,α∈(V T∪V N*)}d. L(G)={α|S+?α, α∈(V T∪V N*)}3、有限状态⾃动机能识别。

a. 上下⽂⽆关⽂法b. 上下⽂有关⽂法c.正规⽂法d. 短语⽂法4、设G为算符优先⽂法，G的任意终结符对a、b有以下关系成⽴。

a. 若f(a)>g(b)，则a>bb.若f(a)c. a~b都不⼀定成⽴d. a~b⼀定成⽴5、如果⽂法G是⽆⼆义的，则它的任何句⼦α。

a. 最左推导和最右推导对应的语法树必定相同b. 最左推导和最右推导对应的语法树可能不同c. 最左推导和最右推导必定相同d. 可能存在两个不同的最左推导，但它们对应的语法树相同6、由⽂法的开始符经0步或多步推导产⽣的⽂法符号序列是。

第四章语义分析和中间代码生成4.1 完成下列选择题：(1) 四元式之间的联系是通过实现的。

a. 指示器b. 临时变量c. 符号表d. 程序变量(2) 间接三元式表示法的优点为。

a. 采用间接码表，便于优化处理b. 节省存储空间，不便于表的修改c. 便于优化处理，节省存储空间d. 节省存储空间，不便于优化处理(3) 表达式(┐A∨B)∧(C∨D)的逆波兰表示为。

a. ┐AB∨∧CD∨b. A┐B∨CD∨∧c. AB∨┐CD∨∧d. A┐B∨∧CD∨(4) 有一语法制导翻译如下所示：S→bAb {print″1″}A→(B {print″2″}A→a {print″3″}B→Aa) {print″4″}若输入序列为b(((aa)a)a)b，且采用自下而上的分析方法，则输出序列为。

a. 32224441 b. 34242421c. 12424243d. 34442212【解答】(1) b (2) a (3) b (4) b4.2 何谓“语法制导翻译”？试给出用语法制导翻译生成中间代码的要点，并用一简例予以说明。

【解答】语法制导翻译(SDTS)直观上说就是为每个产生式配上一个翻译子程序(称语义动作或语义子程序)，并且在语法分析的同时执行这些子程序。

也即在语法分析过程中，当一个产生式获得匹配(对于自上而下分析)或用于归约(对于自下而上分析)时，此产生式相应的语义子程序进入工作，完成既定的翻译任务。

用语法制导翻译(SDTS)生成中间代码的要点如下：(1) 按语法成分的实际处理顺序生成，即按语义要求生成中间代码。

(2) 注意地址返填问题。

(3) 不要遗漏必要的处理，如无条件跳转等。

例如下面的程序段：if (i>0) a=i+e-b*d; else a=0;在生成中间代码时，条件“i>0”为假的转移地址无法确定，而要等到处理“else”时方可确定，这时就存在一个地址返填问题。

此外，按语义要求，当处理完(i>0)后的语句(即“i>0”为真时执行的语句)时，则应转出当前的if语句，也即此时应加入一条无条件跳转指令，并且这个转移地址也需要待处理完else之后的语句后方可获得，就是说同样存在着地址返填问题。

编译原理龙书第四章答案
1.什么是有效性检查？
答：有效性检查是语法分析中的一项重要检查，是指检查语言结构中
的各部分是否有效，即结构是否符合语言的语法规则。

2.什么是语法分析？
答：语法分析是指将文法定义的模式应用到给定的输入字符串中来识
别出输入字符串的结构特征，以确定给定的输入是否符合语法定义。

3.扩展BNF与简化后的BNF有什么区别？
答：扩展BNF使用更多的符号，可以更准确地表示文法的定义；而简
化后的BNF则把文法的定义层次降低，使用更少的符号，实现文法简化。

4.语法分析生成器的工作原理是什么？
答：语法分析生成器使用上下文无关文法定义的语句，根据文法定义
生成语法分析程序，它包括词法分析器和语法分析器。

当词法分析器处理
输入的字符串时，语法分析器就自动检查输入字符串是否满足文法定义。

5.什么是四元式？
答：四元式是源程序翻译成中间代码的基本单位，它用四元组的形式：(操作码，运算数1，运算数2，结果)来表示一条指令，便于后续的代码
优化和目标代码生成。

6.什么是类型检查？
答：类型检查是指在语义分析中，用来检查程序中表达式和变量的类
型是否合理。