正比例和反比例定义

正比例与反比例关系的应用正比例与反比例关系是数学中常见的概念，它们在实际生活中有着广泛的应用。

本文将介绍正比例与反比例关系的基本概念、特点以及具体的应用场景。

一、正比例关系正比例关系是指两个量之间的变化呈现出一致的比例关系，即当一个量增大（或减小）时，另一个量也相应地增大（或减小）。

在数学上，正比例关系可以用直线方程y = kx 来表示，其中k 表示比例常数。

正比例关系在实际生活中有着丰富的应用，例如：1. 面积与边长的关系：一个平面图形的面积与其边长之间通常呈现出正比例关系。

例如，一个正方形的面积等于边长的平方，一个圆的面积等于半径的平方乘以π。

2. 速度与时间的关系：当一个物体保持匀速运动时，它的位移与时间呈正比。

例如，一个行驶在直线上的车辆，它的速度是恒定的，那么它行驶的距离与所用的时间呈正比。

3. 商品价格与数量的关系：在某些情况下，商品的价格与购买的数量之间呈正比。

例如，某种商品的价格如果为10元，那么购买两个就需要20元，购买三个就需要30元。

二、反比例关系反比例关系是指两个量之间的变化呈现出相互制约的关系，即当一个量增大（或减小）时，另一个量相应地减小（或增大）。

在数学上，反比例关系可以用直线方程 y = k/x 来表示，其中 k 表示比例常数。

反比例关系在实际生活中也具有广泛的应用，例如：1. 速度与时间的关系：当一个物体在规定时间内完成固定距离的运动时，它的速度与所用的时间呈反比。

即速度越快，所用的时间越短。

2. 工人数量与工作时间的关系：在某项工作中，如果增加工人的数量，工作所需的时间会减少，反之亦然。

这是因为工人数量的增加可以提高工作的效率。

3. 水流与管道宽度的关系：水流通过一个管道时，水流的速度与管道的宽度呈反比。

如果管道变窄，水流的速度将增加，反之亦然。

综上所述，正比例与反比例关系在生活中有着广泛的应用。

了解这些关系可以帮助我们更好地理解和解决实际问题，提高数学应用的能力。

正比例与反比例的概念与计算正比例与反比例是数学中常见的概念，它们在日常生活和各个学科中都有广泛的应用。

本文将详细介绍正比例与反比例的概念以及相关的计算方法，并给出一些实际例子，以帮助读者更好地理解和运用这些概念。

一、正比例的概念与计算正比例是指两个变量之间的关系，当一个变量增加时，另一个变量也相应地增加，它们之间存在着恒定的比例关系。

假设我们有两个变量x和y，它们之间的正比例关系可以表示为y = kx，其中k是常数，称为比例常数。

在这种情况下，无论x和y的具体取值如何，它们的比值始终保持不变。

为了更好地理解正比例的概念，我们可以考虑一个简单的例子。

假设小明每天骑自行车上学的时间与他家离学校的距离之间存在着正比例关系。

如果我们用x表示上学的时间（小时），用y表示离学校的距离（千米），那么我们可以将它们的关系表示为y = kx。

实际上，k 代表的就是小明骑自行车的速度（千米/小时）。

无论小明上学的时间和离学校的距离具体是多少，他的骑行速度始终保持不变。

在计算正比例关系时，我们可以通过已知的一组数据来确定比例常数k的值。

例如，如果我们知道小明骑自行车上学的时间为2小时，离学校的距离为10千米，那么我们可以将这组数据代入到比例关系式y = kx中，得到10 = 2k，从而求得k的值为5。

这样一来，我们就可以根据这个比例关系来计算其他未知条件下的数值。

二、反比例的概念与计算与正比例不同，反比例是指两个变量之间的关系，当一个变量增加时，另一个变量相应地减少，并且它们之间的乘积保持不变。

如果我们有两个变量x和y，它们之间的反比例关系可以表示为xy = k，其中k是常数。

在这种情况下，当x增加时，y会相应地减少，反之亦然。

为了更好地理解反比例的概念，我们可以举一个简单的例子。

假设小明骑自行车的速度与他到达目的地所用的时间之间存在反比例关系。

如果我们用x表示速度（千米/小时），用y表示所需的时间（小时），那么我们可以将它们的关系表示为xy = k。

正比例和反比例的概念物理1. 什么是正比例？正比例，简单说就是两个量成正比。

比如说，想象一下你在超市买水果，苹果的价格跟你买的数量成正比例关系。

如果一个苹果五块钱，买十个就是五十块钱，买二十个就是一百块钱，数量增加，价格也跟着蹭蹭往上涨，嘿，这就叫正比例。

生活中这种情况比比皆是，比如车速和行驶时间的关系：你开得越快，时间就越短，真是越快越省事！这就让人想起“欲速则不达”这句老话，虽然快很重要，但得掌握好节奏啊。

1.1 正比例的例子生活中有很多正比例的例子，比如吃饭的量和饭钱。

想想你去自助餐，吃得越多，花的钱自然也多，没啥好说的！再比如说，行李的重量和你飞机票的费用，如果你超重了，机场可不管你是不是为了带特产，得补差价。

还有电费，家里电器用得多，电费就得多掏钱。

其实，正比例在生活中无处不在，就像空气一样，你看不见，但它确实存在。

1.2 正比例的公式在数学上，我们用一个简单的公式来表示正比例关系：y = kx。

这里的k就是比例系数，代表每增加一个单位x，y就增加k个单位。

这就像是你和朋友打赌，你说“我能在五分钟内吃完这个汉堡”，你的朋友说“那我就等着看你怎么被呛到”，哈哈！这中间的关系就能用正比例来解释。

2. 反比例的概念相对而言，反比例就是两个量的关系恰好相反。

当一个量增加时，另一个量就减少。

举个简单的例子，想象你在赛道上跑步，跑得越快，完成比赛的时间就越短，这就是反比例。

如果你一路飞奔，像风一样迅速，最后时间就少得可怜，这种关系简直像是“此消彼长”，让人觉得妙不可言。

2.1 反比例的例子再想想，我们每天都得喝水吧？如果你一天只喝一杯水，身体就会缺水，越缺水就越渴。

而你喝得多，身体反而会保持水分。

类似的，咱们的学习和考试时间也是反比例关系，时间越少，压力就越大，结果有可能就掉链子了。

生活中处处都是反比例的影子，像一场无声的较量。

2.2 反比例的公式在数学上，反比例也有个公式：y = k/x。

这里的k依旧是比例系数，这个关系可真是让人捉摸不透，像一场无形的博弈。

六年级数学下册正比例和反比例知识点一、内容概要正比例和反比例是六年级数学下册的重要知识点，简单来说正比例表示两个量成正比关系，当一个量增加时，另一个量也会增加，反之亦然。

好比速度和时间是常见的正比例例子，当速度加快时，需要的时间就会减少。

反比例则是当两个量中的其中一个增加时，另一个会减少。

像是你在爬山过程中体力消耗与海拔高度的关系，海拔越高体力消耗越大，反之越省力就是反比例的例子。

掌握这些知识可以帮助我们更好地理解生活中的各种现象，接下来我们将详细解析这两个概念的应用和解题方法。

1. 回顾数学基础知识，为学习正比例和反比例做铺垫亲爱的小朋友们，转眼间我们已经进入了六年级的数学之旅，那么今天我们来一起回顾一下前面学过的数学知识，为接下来要学习的正比例和反比例知识点做好铺垫吧！数学的世界总是充满了神奇的奥秘，让我们一步步走进这个奇妙的世界。

我们知道数学是生活中的一把钥匙，它能帮助我们解决很多有趣的问题。

在学习正比例和反比例之前，我们要先打好基础。

回顾一下我们之前学过的关于数量和数量之间的关系的知识，比如当我们买文具时，文具的数量和总价之间就有一种特殊的关系。

买一支笔和买十支笔的价格是不一样的，这就是数量和价格之间的关系。

这就是我们接下来要学习的正比例和反比例的基础，你们准备好了吗？接下来我们要更深入地去探索这种关系的奥秘！2. 简述正比例和反比例的概念及其在实际生活中的应用反比例呢？它与正比例相反，当一个量变大时，另一个量就会变小。

比如说你在调节电视机的音量和亮度时，通常音量越大，电视屏幕的亮度就越低，因为电视的音量和亮度就是一对反比例关系。

再如开车的时候，车速越慢反而里程消耗越多；一个钟表转得越慢它行走的总圈数就越大等生活中都可以发现反比例的例子。

明白正比例和反比例的概念后，我们就可以更好地理解和解决生活中的很多问题啦！二、正比例知识点我们知道生活中有很多事物之间是有关系的，比如你吃的零食越多，肚子就越容易饱。

正比例与反比例正比例两种相关联的量，一种量变化，另一种量也随着变化，如果两种量中相对应的两个数的比值(商)一定，这两种量就叫做成正比例的量，他们的关系叫做正比例关系。

如果用字母x 和y表示两种关联的量，用k表示它们的比值，成正比例关系可以用下面式子表示：y/x=k （一定）反比例两种相关联的量，一种量变化，另一种量也随着变化，如果两种量中相对应的两个数的乘积一定，这两种量就叫做成反比例的量，他们的关系叫做反比例关系。

如果用字母x和y 表示两种关联的量，用k表示它们的乘积，成反比例关系可以用下面式子表示：xy=k（一定）反比例性的概念可以与直接相称性进行对比。

考虑两个变量被认为是“相互成比例”的。

如果所有其他变量保持不变，如果另一个变量增加，则一个反比例变量的幅度或绝对值减小，而其乘积（比例常数k）总是相同的。

如果每个变量与另一个变量的乘数相反（倒数）成正比，则两个变量成反比（也称为反向变化，反向变异，反比例），如果其乘积是一个常数。

因此，如果存在非零常数k，则变量y与变量x成反比：或等价于。

因此，常数是x和y的乘积。

例如，旅途所需的时间与旅行速度成反比；挖洞所需的时间（大概）与挖掘人数成反比。

在笛卡尔坐标平面上反向变化的两个变量的曲线图是矩形双曲线。

曲线上每个点的x 和y值的乘积等于比例常数（k）。

既然x和y都不能等于零（因为k是非零），所以图形从不跨任一个轴。

如何判断在解决此类问题过程中要紧紧抓住正反比例的意义，一是看不是两种相关联的量，二看这两个量之间的商一定还是积一定的。

商一定，两个量成正比例；积一定，两个量成反比例。

其次在解决实践应用问题时要注意比和比例，以及它们和分数之间的关系。

然后再综合所学过的知识进行解答。

正比例与反比例的判断方法一、正比例的判断方法正比例是指两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值 (商) 一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

判断正比例的方法如下:1. 找变量：确定哪两种量是相关联的量。

2. 看定量：分析这两种相关联的量，它们之间的关系是商一定还是积一定。

3. 判断：如果商一定，就成正比例;如果积一定，就成反比例;如果商和积都不是定量，就不成比例。

举个例子，假设小明的身高和他的体重成正比例，即小明的身高每增加 1 厘米，他的体重就会增加一定的值。

假设小明的身高为 170 厘米，他的体重为 70 公斤，那么根据正比例的关系，小明的体重和身高的比值应该是 70/170，这是一个定值。

因此，我们可以得出结论，小明的身高和他的体重成正比例。

二、反比例的判断方法反比例是指两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系。

判断反比例的方法如下:1. 找变量：确定哪两种量是相关联的量。

2. 看定量：分析这两种相关联的量，它们之间的关系是商一定还是积一定。

3. 判断：如果积一定，就成反比例;如果商一定，就不成比例;如果商和积都不是定量，就不成比例。

举个例子，假设小明的学习时间和他的成绩成正比例，即小明的学习时间每增加 1 小时，他的成绩就会增加一定的值。

假设小明的学习时间分别为 1 小时、2 小时、3 小时，他的成绩分别为 80 分、90 分、100 分，那么根据反比例的关系，小明的学习时间和他的成绩的积应该是一个定值。

假设小明的学习时间分别为 1 小时、2 小时、3 小时，他的成绩分别为 80 分、90 分、100 分，那么根据反比例的关系，小明的学习时间和他的成绩的积应该是一个定值。

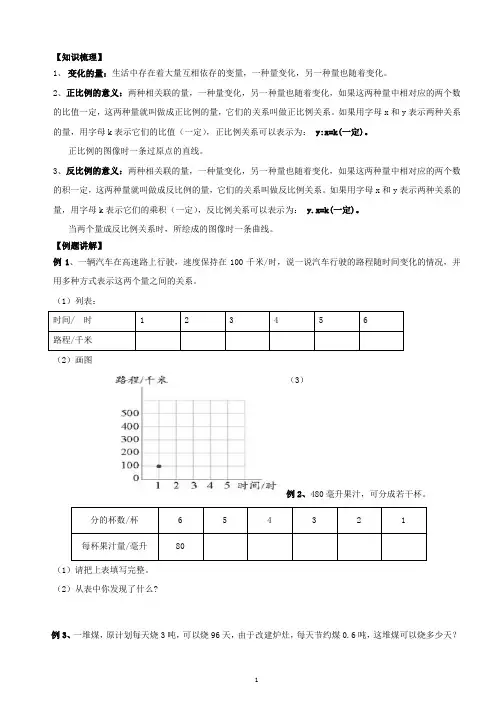
【知识梳理】1、变化的量：生活中存在着大量互相依存的变量，一种量变化，另一种量也随着变化。

2、正比例的意义：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

如果用字母x和y表示两种关系的量，用字母k表示它们的比值（一定），正比例关系可以表示为： y:x=k(一定)。

正比例的图像时一条过原点的直线。

3、反比例的意义：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系。

如果用字母x和y表示两种关系的量，用字母k表示它们的乘积（一定），反比例关系可以表示为： y.x=k(一定)。

当两个量成反比例关系时，所绘成的图像时一条曲线。

【例题讲解】例1、一辆汽车在高速路上行驶，速度保持在100千米/时，说一说汽车行驶的路程随时间变化的情况，并用多种方式表示这两个量之间的关系。

（1）列表：时间/ 时 1 2 3 4 5 6路程/千米（2）画图（3）例2、480毫升果汁，可分成若干杯。

分的杯数/杯 6 5 4 3 2 1每杯果汁量/毫升80（1）请把上表填写完整。

（2）从表中你发现了什么?例3、一堆煤，原计划每天烧3吨，可以烧96天，由于改建炉灶，每天节约煤0.6吨，这堆煤可以烧多少天？课堂练习：一、我会填：1、a×b=c,当a一定时，a和b成比例，当b一定时，和成比例。

2、和一定时，一个加数和另一个加数比例。

3、（1）速度×（）=路程（）÷（）=时间（）÷（）=速度（2）工作效率×工作时间=（）（）÷（）=工作效率（）÷（）=工作时间（3）（）×数量=总价（）÷（）=数量（）÷（）=单价4、圆柱的底面积一定，它的体积和高成（）关系。

5、播种的总公顷数÷天数=每天播种的总公顷数。